Теоретическое исследование интенсивности нагрузки и натяжения при баллонировании комбинированной электропроводящей нити

В процессе кручения участок нити между нитепроводником и бегунком вращается с частотой вращения бегунка вокруг оси, находящейся в вертикальной плоскости. Под влиянием центробежных сил, действующих перпендикулярно оси вращения, нить отбрасывается в сторону и принимает выпуклую форму, описывая в пространстве баллон.

Нить преодолевает значительные силы трения бегунка о кольцо, так как при увеличении угловой скорости бегунка возникает большая центробежная сила, прижимающая его к кольцу. Кроме центробежных сил на нить действует сила сопротивления воздуха, масса нити, сила Кориолиса (вследствие относительного и переносного движения нити).

Наиболее полно механика гибкой нити изложена в работах А.П. Минакова, И.И. Мигушова [1], Ю.В. Якубовского [2] и др. Вопросами теории процесса баллонирования на текстильном оборудовании занимались Н.Е. Жуковский, П.Ф. Ерченко, А.Н. Васильев [3], А.Г. Коган [4], А.А. Баранова [5], Н.Н. Бадяло [6] и др. Специфика разработанного процесса формирования крученых комбинированных нитей на тростильно-крутильных машинах вызвала необходимость тщательного изучения процесса баллонирования нити первичной и вторичной крутки и разработки нового аналитического метода определения их натяжения в баллоне. Процесс сматывания нити с равномерно вращающейся паковки будем рассматривать как установившееся вращательное движение с постоянной угловой скоростью ω . На участке от бобины до шпинделя веретена комбинированная нить в результате вращения получает форму баллона АВD (рисунок 1).

Рисунок 1 – Расчетная схема движения нити

Таким образом, образующую баллон нить будем рассматривать как гибкую материальную линию, которая не искривляется от сопротивления воздуха и расположена в вертикальной плоскости. При анализе также не учитываем силу Кориолиса, величина которой незначительна вследствие малой продольной скорости движения нити. Тогда на баллонирующую нить действуют центробежная сила и сила тяжести.

Центробежную силу, действующую на единицу длины нити, можно определить по формуле:

F = mw x ,                          (3.62)

где m – масса единицы длины нити, кг;

x i - радиус баллона элемента нити, м.

го - угловая скорость вращения веретена, с^-1.

to =

П П ВР

где n ВР – частота вращения веретена, мин^-1.

Определим длину нити в баллоне при разных положениях кольцевой планки. При верхнем положении кольцевой планки длина нити в баллоне практически совпадает с длиной нити в статическом положении. Следовательно, зная радиус кольца (0,0625 м) и высоту баллона, можно определить длину нити в баллоне L min .

При определение интенсивности нагрузки при баллонировании комбинированной электропроводящей нити представим нить как изогнутую балку и воспользуемся дифференциальным уравнением упругой линии балки (нити) [7 стр 165]:

F ц    mw ² x _i

q =----= —--- (Н/м), in var in var где L- длина нити в баллоне, м

L min qmax

Представим схему нагружения нити как упругую балку на опорах, нагруженную равномерно распределенной нагрузкой q.

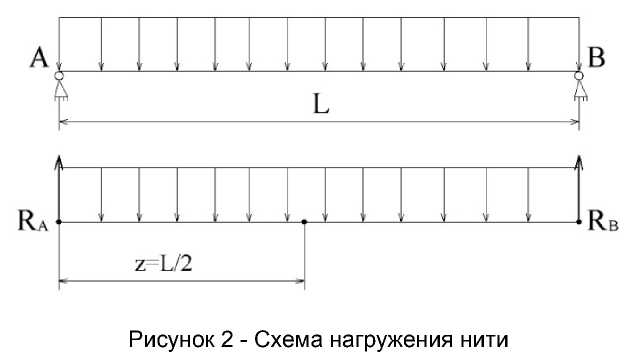
Опорные реакции при такой схеме нагружения равны:

R A

= Rb =

q • L

Изгибающий момент от действия центробежных сил интенсивностью q в сечении z (см. рис 2) М z определяется равенством:

M z = R a • z

q • z2 —

Где 0 < z < L

Mz =

q • L • z

q • z²

q2z (L - z)

Форму изогнутой оси балки или форму упругой линии можно определить при помощи выражения

1 = Мz

p   Еэкв Jx экв где Еэкв- эквивалентный модуль упругости комбинированной электропроводящей нити крутки ;

J xэкв - эквивалентный момент инерции комбинированной электропроводящей нити.

В неподвижной системе координат у, z

1= y

3/

^p (1 + у^Y'-

Решением дифференциального уравнения для заданной схемы нагружения имеет вид [8 стр. 79].

y =

q экв xэкв

2 Lz3 - z4 - L3 z

при 0 < z < L

Определим геометрические и механические характеристики нити.

Модули упругости исходных компонентов комбинированной нити представлены в таблице 1.

Таблица 1 - Модули упругости исходных компонентов комбинированной нити

Показатель	Модуль упругости, МПа
Нити полиэфирные
Высокой прочности (сердечник)	13500-16000
Средней прочности (покрывающий компонент)	12000-14000
Медная микропроволока	120000-130000

Момент инерции для круга определим по формулам:

n d 4

J xэкв

Где d- диаметр нити, м

Диаметр нити первичной крутки определяется по формуле:

d1 = 0,0357

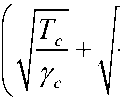
I м.пр м.пр

^Y м. пр

Е экв J экв – определяем из условия равных деформаций всех компонентов, входящих в систему.

Тогда для нити первичной крутки можно записать:

E • T E • T экв экв с с

E -J м.пр    м.пр

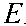
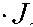
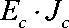
• E • J м.пр    м.пр

;

^ м . пр м пр . пр + ^ с с с

Где Е с - модуль упругости сердечника (упрочненной полиэфирной нити); J хс - момент инерции сердечника (упрочненной полиэфирной нити).

Для нити вторичной крутки

-----=----+--------+----

: J Е -J Е -J Е J экв экв с с       м . пр м . пр       п п

Е с • J с ■ Е м • J м • Е п ■ J п

^п п п мм . пр м М . пр ⁺ ^ с с С п п ^ п ⁺ ^ с с С мпр . пр м м . пр

Максимальный прогиб баллона определяется при

L

z = —

по формуле:

5qL4

У =--

384E J экв экв

При помощи фото- и видеосъемки (см. рис. 3) определены высота баллона, максимальные радиусы баллонирующей нити и величина прогиба в трех положениях кольцевой планки (в нижнем, среднем и верхнем положении). Данные приведены в таблице 2.

а)- нижнее

б) верхнее

в) среднее

Рисунок 3 – Фотографии баллонирующей электропроводящей нити в различных положениях кольцевой планки

Таблица 2 – Экспериментальные геометрические параметры баллона при различных положениях кольцевой планки

Параметры	Нижнее положение	Среднее положение	Верхнее положение
Высота баллона, м.	0,5	0,365	0,23
Максимальный радиус баллона, м.
Нити первичной крутки	0,091	0,071	0,0635
Нити вторичной крутки	0,105	0,0747	0,0648
Величина максимального прогиба, м
Нити первичной крутки	0,0285	0,0084	0,00145
Нити вторичной крутки	0,0425	0,0122	0,0023

Для различных положений кольцевой планки наблюдается хорошее совпадение результатов эксперимента и расчетных. Ошибка не превышает 6%.

Углы поворота в крайних точках сечения баллона определяются по формулам 16 – 17 [8 стр. 79]:

β =   qL3

экв xэкв

^β 2 ⁼

qL ³

J экв xэкв

При сравнении расчетных и экспериментальных параметров угла прогиба нити первичной и вторичной крутки при разных положениях кольцевой планки ошибка не превышает 6%, что подтверждает правильность выбора расчетных моделей.

Максимальная сила натяжения нити Р, возникающая при производстве комбинированной электропроводящей нити на тростильно-крутильной машине, действует в нижней части баллона около бегунка и определяется по формуле 18 [1].

Р =        mw2r

ef⋅β ⋅(sinα/µ+cosα)-1

где m - масса бегунка, г; r – радиус кольца, см;

w – угловая скорость бегунка вокруг веретена, с^-1;

f – коэффициент трения нити о бегунок;

β – угол поворота в крайних точках сечения баллона;

α – угол, определяющий соотношения между радиусами намотки и кольца;

• μ – коэффициент трения бегунка о кольцо;

Из формулы (18) видно, что натяжение нити прямо пропорционально квадрату угловой скорости бегунка, его массе и радиусу кольца. С увеличением коэффициента трения между бегунком и кольцом натяжение нити увеличивается, оно зависит также от соотношения между радиусами намотки и кольца (угол α ).

Используя данные таблицы 2 и расчетные величины угла поворота в крайних точках сечения баллона, проведем расчет натяжения комбинированной нити первичной и вторичной крутки в 3-х положениях кольцевой планки.

После расчета приведена таблица 3, в которой представлены натяжения нити в зависимости от положения кольцевой планки.

Таблица 3– Натяжения нити в зависимости от положения кольцевой планки и радиуса намотки нити на паковке

Положение кольцевой планки	Радиус намотки нити на паковке	Натяжение нити, сН
нижнее	минимальный	84,2
нижнее	средний	63,9
нижнее	максимальный	54,1
среднее	минимальный	84,9
среднее	средний	64,4
среднее	максимальный	54,5
верхнее	минимальный	86,5
верхнее	средний	65,5
верхнее	максимальный	55,3

В результате расчета установлено, что в нижнем, среднем и верхнем положении кольцевой планки при минимальном радиусе намотки натяжение комбинированной нити максимальное – 80 – 90 сН, при среднем радиусе намотки натяжение – 60 – 70 сН, а при максимальном радиусе намотки натяжение минимальное и примерно равно во всех положениях кольцевой планки – 50 – 60 сН.

При анализе процесса натяжения комбинированных электропроводящих нитей на тростильно-крутильных машинах установлено, что натяжение на рассмотренном участке процесса меньше разрывной нагрузки, следовательно, при заданных (рекомендуемых) параметрах натяжения формирование комбинированной электропроводящей нити будет происходить с необходимыми характеристиками и минимальным обрывом.