Теоретическое исследование процесса взаимодействия древесного сырья с рабочим органом дисковой рубительной машины

Одним из важнейших видов продукции первичной переработки древесины является технологическая щепа, служащая важнейшим сырьем для целлюлозно-бумажной промышленности [9]. От качества производимой щепы значительно зависит качество конечной продукции – бумаги и картона.

Для производства щепы используются различные рубительные машины, в первую очередь – дисковые [2], [8]. Они характеризуются относительной простотой устройства, надежностью и стабильно стью работы, высокой производительностью. Важнейшими направлениями модернизации таких машин являются обеспечение снижения потерь древесины при производстве щепы и улучшение ее фракционного состава. В контексте данных направлений важнейшую роль на качество щепы оказывают конструктивные параметры рубительных машин и в первую очередь – конструкции дисков и самих ножей. Конструктивные особенности дисков и ножей в первую очередь различаются геометрией их формы. В настоящее время наибольшее распростране-

ние получили плоские диски с обычными прямыми ножами. В процессе работы машины древесина через загрузочный патрон, сориентированный определенным образом относительно вращающегося от электродвигателя диска, вступает во взаимодействие с передней и задней гранью режущих ножей, закрепляемых на диске. При этом происходит отруб (срезание) слоя древесины с одновременным самозатягиванием бревна. Затем во взаимодействие с бревном вступает следующий нож. Процесс повторяется до полного измельчения исходного древесного материала в щепу. Щепа при этом удаляется из кожуха рубительного диска либо вверх, либо в сторону.

Проведенные нами наблюдения за работой дисковых рубительных машин, эксплуатируемых на ОАО «Кондопога» и ОАО «Петрозаводский ДОК», с последующим анализом полученного фракционного состава щепы показали, что при использовании обычных плоских дисков с ножами прямой заточки количество щепы крупной и мелкой фракций было достаточно велико

[4]. На наш взгляд, причиной этого являются неравномерности и срывы подачи бревна само-затягиванием к рубительному диску. При падении бревен с подающего транспортера в загрузочный патрон машины происходят значительные биения бревна с ударами о стенки патрона. Эти биения особенно характерны для случая измельчения бревен малого размера (в сравнении с размерами загрузочного патрона) и реек – отходов лесопиления. Такой материал при биениях разворачивается в патроне, вследствие чего на выходе из машины получается щепа некондиционных размеров и формы.

В случаях падения в загрузочный патрон бревен большого диаметра разворота и биения практически не происходит. Однако в этом случае часто наблюдаются срывы подачи, которые приводят к срывам процесса самозатягивания (подачи) и снижению качества фракционного состава щепы. С целью выявления причин этих явлений нами были проведены теоретические исследования процесса взаимодействия бревен с рабочей поверхно стью диска рубительной машины.

Основываясь на теоретических предпосылках взаимодействия режущих ножей с древесиной, изложенных в работах [1], [3], [6], [7], рассмотрим случай поступления в загрузочный патрон бревна малого диаметра (не более 10 % от размера поперечного сечения загрузочного патрона). При контакте с телом диска бревно неизбежно вступает во взаимодействие с закрепленным на диске ножом. Полагаем, что в этот момент ось бревна AB (рис. 1) сориентирована по загрузочному патрону, положение которого относительно плоскости диска характеризуется углами α 1 и α 2 . Таким образом, ось бревна AB образует с осями координат углы α x , α y и α z .

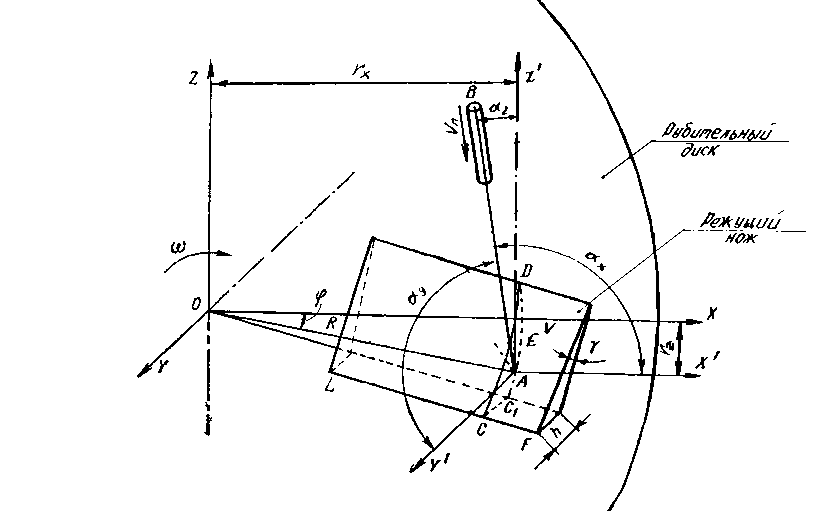
Рис. 1. Схема взаимодействия ножа с бревном малого диаметра

Лезвие ножа LF направлено по радиусу диска, вращающегося относительно оси OY с постоянной угловой скоростью ω, что соответствует установившемуся режиму работы рубительной машины. Задняя грань ножа υ наклонена к плоскости самого диска под углом γ, обеспечивающим процесс затягивания бревна. Лезвие выпущено за пло скость диска на величину h. При повороте ножа с диском ось бревна будет находиться в контакте с задней гранью. При этом на грани она описывает дугу CЕD. Спроецировав эту дугу на плоскость ZOX, получим дугу окружности радиуса резания R. При этих условиях изменение координат центра бревен, а следова- тельно, и скорости подачи будет происходить не прямо пропорционально изменению угла затягивания γ, как, например, в механизмах, осуществляющих строгание древесины.

Определим скоро сть подачи (затягивания) υ n оси бревна. Для этого опишем текущие координаты точки Е (x, y, z) , принадлежащей дуге CЕD . Дуга CЕD образована пересечением с пло ско стью υ линий, проведенных из соответствующих точек дуги C 1 AD и параллельных AB . Координаты точки A , расположенной на диске, (r _x , r _z ) считаем заданными и соответствующими ориентации расположения загрузочного патрона.

В принятой системе координат уравнения линии LF (лезвия) имеют следующий вид:

y = h;

z = - x tg ф ;

y - h = 0;

z + x tg ф = 0.

Уравнение плоскости задней грани ножа и , проходящей через линию LF и плоскость диска, можно записать в следующей форме:

( y - h ) + A ( z + x tg ф ) = x;

Я tg ф + y + A ;                        (2)

z - h = 0.

Значение параметра X , введенного Вальщи-ковым [1], определяется по формуле

A = tg Y cos ф .                  (3)

Подставив значение X в уравнение (2), получим уравнение плоскости задней грани ножа в

следующем виде:

xtg Y tg ф cos ф + y + ztg y cos ф - h = = xtg Y sin Ф + y + ztg Y cos ф - h = 0.

Зная уравнение прямой AВ, пересекающей плоскость в точке Е, x - Г y - 0 z + r

----x- = ----=----- ^z- = C,          (5) cos a cos a cos a xyz

определим координаты самой точки Е(x, y, z)

x = Ccos a x + r x ;

y = C cos a _y;

z = C cos a - r.

zz

Подставляя полученные значения координат в уравнение (4), получим:

( Ccos a x + r x ) tg Y sin ф + Ccos a y +

+ ( C cos a _z - r_z ) tg Y cos ф - h = 0

C =

cos a

x

- rx. tg Y sin ф + r_z tg Y cos ф + h tg Y sin ф + cos a _y + cos a _z tg Y cos ф

где

( - r_x tg Y cos ф - r z tg Y sin ф ) N i + ( r_x tg Y sin ф + r z tg Y cos ф + h ) N ^Ф =                      Q 2

Q = cos a x tg Y sin ф + cos a y + cos a z tg Y cos ф .

N = cos a _x tg Y cos ф - cos a _z tg Y sin ф .

Зная покоординатные составляющие скорости подачи оси бревна, полное ее значение и n в момент отруба при радиальном положении ножей определим по известному кинематическому соотношению

U n = ^u+^ u +^ u ..            ⁽⁹⁾

Очевидно, что бревно или рейка, вступая в контакт с ножом и имея свободу разворота в загрузочном патроне (особенно при небольших продольных размерах), приобретают значительные величины скоростей точки пересечения своей оси с плоскостью ножа в направлении осей X и Y (см. уравнения 8). Эти составляющие общей скорости подачи (самозатягивания) и приводят к развороту бревна в загрузочном патроне, вызывая его рубку под углом с образованием относительно длинных частиц щепы некондиционной фракции.

Несомненно, что какое-либо изменение геометрии формы диска и формы заточки ножей не позволит устранить этот недостаток.

В случае падения в загрузочный патрон бревна больших размеров, а тем более бревна, размеры которого сопоставимы с размерами горловины загрузочного патрона (рис. 2), разворот его относительно оси подачи, обусловленный биением, невозможен, и бревно практически прямо движется на диск в соответствии с углами ориентировки загрузочного патрона.

Согласно ориентации загрузочного патрона ( а 1 и а ₂), кривые отруба будут проектироваться на плоскость диска в форме эллипсов, имеющих оси

2а = ^и 2b = —-- (10)

cos a 1           cos a 2

При непрерывном контакте древесины с задними пло скостями ножей (установившийся режим работы) линии отруба также будут иметь вид эллипсов (с точками Е 1 , Е 2 ), полученных путем пересечения прямыми линиями, образующими цилиндр (бревно), плоскости и .

Уравнения линии лезвия LF , как и в предыдущем случае, имеют вид (1).

Уравнение эллипса резания в системе координат Z'AX ' :

Взяв производные от координат x, y, z по времени, получим значение составляющих скорости подачи (затягивания) оси бревна и = го Ф cosa , и = ®Ф cos a,, U = юФ cos a; (8) x xyyz z

22 x²z²

—т +—г = 1; b²a²

y = 0;

или

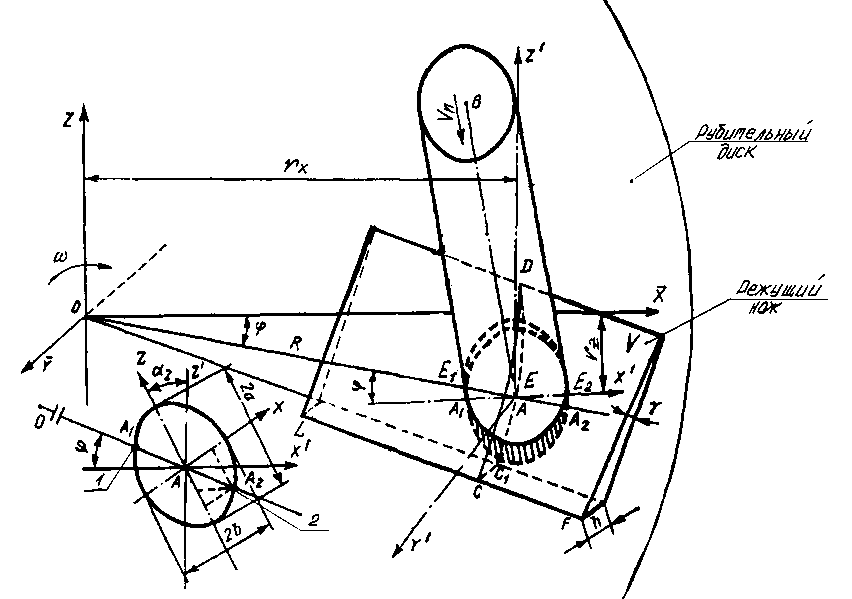
Рис. 2. Схема взаимодействия ножа с бревном максимального диаметра

U — 4U 2 + и 2 + U 2 . (13) n 1 2 x 1 2 y 1 2 z 1 2

2 2   22   22

a x + b z — a b — 0.

Совместным решением уравнений эллипсов резания и линии лезвия режущих ножей определяются координаты точек Е 1 и Е 2 .

Дифференцируя их по времени, получим выражения для координатных составляющих скоростей подачи (затягивания):

^{U  — Ф} б cos « x - x 12 ;

^и У 12 ^— Ф б c^{OS a} y ;

^U z = ^Ф б cos ^ - z 1 ₃ ;

где

^Фб —

— x₁ 2 Е + z₁ 2 D — tg y ( m sin p + n cos p )

F

;

E — tg y sin ( p — a ₂ ) ;

D — tg y cos ( p — a ₂ ) ;

F — cos a x sin ( p — a ₂ ) tg y + cos a y + cos a z cos ( p — a ₂ ) tg y .

Зная покоординатные составляющие скорости подачи (12), полное ее значение и _n1,₂ в диаметрально расположенных точках Е 1 , Е 2 в момент отруба определим по известному кинематическому соотношению

Расчеты скоростей, проведенные по формуле (13) для различных параметров рубительных машин, показывают, что при рубке бревен значительных размеров между скоростями диаметрально противоположных точек бревна при его контакте с задней гранью ножа наблюдается явное кинематическое несоответствие. Данное несоответствие скоростей подачи приводит к нестабильности процесса резания, появлению срывов в подаче и ухудшению фракционного состава щепы.

Проведенные расчеты позволили установить, что с увеличением угла поворота диска с 10 до 30 ° (0 ° - момент начала вхождения лезвия в бревно), то есть по мере заглубления ножа в рез, средняя скорость затягивания уменьшается на 20–25 %, что является причиной нестабильности и дальнейшего срыва подачи.

Увеличение радиуса резания вызывает увеличение скорости подачи (затягивания). При этом кинематическое несоответствие перемещений диаметрально противоположных точек бревна сильнее сказывается на машинах с диаметрами дисков до 1500 мм. Так, при рубке бревна диаметром 20 см диском диаметром 1270 мм значения скоростей подачи по крайним точкам составили 2,6 и 1,82 м/c, то есть разница равна 30 %. При использовании диска диаметром 2000 мм для измельчения бревна того же диаметра значения ско- ростей составили 5,4 и 4,6 м/с соответственно, то есть в этом случае разница равна только 15 %.

Для устранения выявленного кинематического несоответствия и создания условий для равномерной подачи бревна самозатягиванием необходимо обеспечить одинаковую скорость подачи на любом радиусе резания и при любом угле поворота диска. Данные условия могут быть выполнены при применении геликоидальной поверхности диска и геликоидальной формы заточки рубительных ножей [5].

Геликоидальная (винтовая) поверхность получается в результате сложного равномерного движения некоторой точки, которая перемещается вдоль образующей поверхности цилиндра, в то время как сама образующая равномерно вращается вокруг оси цилиндра.

Фронтальная проекция цилиндрической геликоиды представляет собой синусоиду с длиной волны, равной шагу , и амплитудой, равной радиусу окружности основания образующего цилиндра.

Развертка части цилиндрической поверхности, ограниченной геликоидой на длине одного витка, представляет собой прямоугольный треугольник. Из прямоугольного треугольника можно легко найти зависимость шага от угла подъема геликоиды для практического расчета ее параметров при проектировании формы диска и формы заточки ножей.

Выполнение геометрической формы диска в виде геликоидальной поверхности и применение геликоидальной формы заточки ножей позволяют устранить кинематическое несоответствие скоростей подачи диаметрально противоположных точек бревна практически на любых диаметрах ру-бительных дисков. Применение геликоидальной формы заточки ножей позволяет также стабилизировать подачу (процесс самозатягивания) независимо от угла поворота диска и избежать эффекта снижения скорости затягивания. Однако следует учитывать, что данный эффект наступает только со второго-третьего отруба.

При использовании рубительных машин с дисками диаметром более 2000 мм и прямыми ножами выявленное кинематическое несоответствие скоростей подачи диаметрально противоположных точек бревна, согласно выполненным расчетам, оказывается незначительным. При этом использование геликоидальной формы заточки ножа становится невозможным из-за уменьшения заднего угла резания ниже допустимого предела (2 ° ).