Теоретическое исследование распространения электромагнитной энергии вдоль провода в выработанном пространстве шахты

Нефтяные шахты являются сложноорганизованными технологическими объектами с рассредоточенными параметрами. Это обуславливается значительной протяженностью горных выработок, большим количеством ответственных установок и систем, а также необходимостью постоянного мониторинга множества показателей, как процесса функционирования оборудования, так и состояния атмосферы в пространстве шахты. При этом важнейшим звеном в цепочке обеспечения управления работой нефтешахтного комплекса является процесс передачи информации внутри шахты и на поверхность. Следует отметить, что, несмотря на особое внимание, уделяемое шахтной разработке нефтяных месторождений, канал связи в выработках обеспечивается устаревшим способом проводной связи. Данный факт можно объяснить недостаточной изученностью процесса распространения радиоволн в тоннелях шахты, что влечет за собой трудности в реализации радиосвязи и обеспечении необходимого качества сигнала.

Примечательно, что внутреннее пространство штреков в шахте зачастую неоднородно и может включать в себя множество металлоконструкций, проводов и установок. Поэтому исследования в области передачи радиосигналов в шахтных условиях с учетом влияния проводящих элементов являются актуальными.

Для теоретического объяснения распространения электромагнитной энергии вдоль провода рассмотрим бесконечный цилиндрический провод с конечной проводимостью, размещенный внутри тоннеля.

Воспользовавшись методом комплексны амплитуд и уравнениями Максвелла, получим в цилиндрической системе координат (Г ,ф ,Z) два волновых уравнения:

д ² E_z д z¹

1 д e    1 д ² e

+   ⋅ z+    ⋅ z r  д r   r2  дф2

+ ( K ² - Y ²) • Ez = 0;

д ² H д z²

1 д H   1 д ² H

+   ⋅ z+    ⋅ z r дr r дф

+ ( K ² - y ²) • Hz = 0,

где E, H - электрическая и магнитная составляющие электромагнитного поля; K – фазовый множитель;γ – постоянная распространения.

Введем обозначения поперечных волновых чисел электрических и магнитных волн для второй среды (т.е. в тоннеле) и для третьей среды (окружающая горная порода):

Р   K ² - y ;

2                           т2

Р = к 2 - y ;

р = к 3 - У ;

Р = кз2 - y\ где Р, Р - поперечное волновое число для магнитных волн внутри и вне тоннеля соответственно;

Р , Р - поперечное волновое число для электрических волн внутри и вне тоннеля соответственно;

Y , Y — постоянные распространения магнитных и электрических волн соответственно.

Пользуясь методом разделения переменных и учитывая принятые обозначения, получим соотношения для решения волновых уравнений:

• -    составляющие поля во второй среде:

II                                                                   II                                                                                II                                 - /     "X

E z = [ « 1 • J n ( Р 2 Р ) + m • N n ( Р 2 Р )] • e^{< Y} '^{+ n ф} ) ;

II                                                                   I                                                                                 I                                 - /     1X

H z = [ в 1 • J n ( Р 2 Р ) + m 2 • N n ( Р 2 Р )] • e^{< Y} • ^{z + n ф} ) ;

Еф =-• [«1 • Jn(Р2р) + m1 • Nn(Р2р)]• e14Y z+nф)

ф

• - ¹ ^.ц_х ^² • [ _д • J ( Р 2 Р ) + m 2 • N n ( р 2 р )] •    _r z ⁺ " ^ф ) ;

c

H ф = - •  •   ^{2   2} • [ « 1 • j n ( Р р ) + m 1 • N n ( Р 2 Р )] • e ^{1 ( Y}' z ⁺ " ^ф ) -

ω µ

• -    ^ ^ 11 в 1 • J n ( р 2 р ) + m 2 • N n ( Р 2 Р )] • e^vY z ⁺ " ^ф ) ; ^ρ

• -    составляющие поля в третьей среде:

III                                                        II                        • /    "X

E z = « 2 ^ H n ( Р з р ) • e'^Y "⁺ " ^ф ) ;

III                                                        I                        • /    'X

H z = P 2- H n ( Р з Р ) • e^HY "⁺ " ^ф ) ;

Е ф =- n^-a.. J'_n ( Р з' p ) • e i< ^Y - ⁺ " ^ф ) +

ρ

• 7 • C • IC _ • P               г,хг I.• г "

+ ^{1 C} A ^{2   Р} 2 • в • J (1) ( Р p ) • e • ^{( Y} - z ⁺ n ^ф ) ;

ω µ

H = г - с - к ф -р^ • a • j (1) ‘ ( р ,p ) ) • e • ⁽ у z + n ^ ) -

• ϕ    ω µ

• - n-^-вз   (P р₃ p ) • e^{< Y} z + ⁺ " ^ф ) .

ρ

Для определения неизвестных коэффициентов « , a , в , в , ^w i , ^w 2 необходимо подчинить вышеприведенные соотношения граничным условиям.

С учетом граничных условий и преобразований, а также с помощью согласования выражений составляющих поля с мощностью излучения получаем выражение мощности передаваемой по тоннелю:

2 п

Pa = A 2 Re J dV J {i • Y" • P2 ' [ai • J0( P2>) + ml • N0( P2P)] • e'Y 'z

0      0

i⋅c⋅K ⋅P

×

ω⋅µ

2 ⁿ

x[a • Jo (P P) + mx • N (P P)] • eY }dp + A2 Re J dp • einv • J i ® ^  2 x

0              0       ^c

х[в- • J0(P2P) + m2 • N0(P2P)] • eY • {----L • - • [ai • J0(P2P) + m- • N0(P2P)] • ei’Y " + ω µ ρ

+i • P2 Y ‘ [в- • J0(P2 P) + m 2 • N0( P2P)] • e ' } dP-

После математических преобразований получаем следующие выражения для определения составляющих поля внутри тоннеля:

^E z = ^B • ^{[ a} 1 • ^J 0 ^{( P} 2 a ) ⁺ m l • ^N 0 ^{( P} 2 a ^)] • e ^Y ’

H z = л Pt • [ в -' • J 0 ( P 2 a ) + m 2 • N a ( P ^ a )] • ^{d Y} ';

Е_Ф = Л PI • i ^‘^/A • P • [ в -' • J 0 ( P 2 a ) + m\ • N ₀( P ^ a )] • e^ z ; Bc

H ₌ P^-a ■ •^{-cK- 1} • P ² . r (p'_a\ ₊ .n'( P    _ei^Y z •

¹¹Ф X       ^a 1                  ^[U0⁽¹2 ^a ) ⁺ m l ^1N 0^(J 2 ^{a )]} e ;

B    ω µ

^{E p} = Pe • ^{[ a} - • ^J 0 ^{( P} 2 ^a ) ^{+ m} • N ° ^{( P} 2 ^{a )]} • e ^Y" ;

P"    ' c ^ K ,²     ,.             '    ' ,,._.      ,

, i Y z .

H ϕ

= a/ • a ---- J й (P 2 a ) + m - Y • N ₀( P 2 a ) • e

Bω µ a

Расчетные значения постоянной распространения γ отражены на рисунке 1. Значения γ дают возможность сделать вывод о том, что наличие металлических направляющих элементов приводит к повышению дальности распространения радиоволн [1].

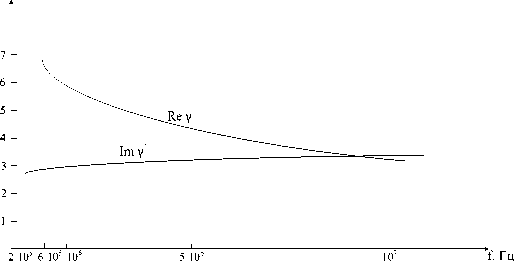
Рис. 1. Частотная зависимость постоянной распространения радиоволн при наличии металлических направляющих элементов.