Теоретическое исследование распространения радиоволн в подземных условиях при отсутствии металлических направляющих элементов

В настоящее время связь между технологическими объектами и диспетчерским пунктом нефтяных шахт, в основном, осуществляется с помощью коммуникаций проводной связи в рудничном исполнении, при использовании которых требуется постоянное присутствие под землей обслуживающего персонала. Увеличение рентабельности нефтешахт и уменьшение времени нахождения обслуживающего персонала под землей и тем самым повышение производительности труда требует применения дистанционного контроля технологических параметров с помощью радиосвязи. При этом следует учитывать, что условия работы подземных антенн во многом отличаются условий работы приземных антенн, процесс излучения которых непосредственным образом связан с окружающей средой. Поэтому при исследованиях подземных антенн с целью выявления особенностей распространения радиоволн необходимо знание значений электрических параметров пород.

В [1] рассмотрен случай распространения радиоволн внутри тоннеля, когда проводимость стены тоннеля считалась бесконечно большой. При этом все математические выкладки существенно упрощаются, так как не учитывается влияние тока смещения. В реальных условиях стены тоннеля нефтяных шахт являются полупроводящей средой [2], для которой постоянная распространения принимает комплексное значение. Анализ выполнен в цилиндрической системе координат ( r , ф , z ) с началом координат на оси цилиндра и рассмотрена гармоническая во времени распространения электромагнитная волна в области, не содержащей сторонних источников ( E = 0).

В результате решения волновых уравнений согласно методике изложенной в [1] определяется поперечное волновое число для электрических и магнитных волн поля внутри и вне тоннеля:

P = КИЛ ;

P =         ;

P , = K^! -        ;

P2 = H—YE ,

'

где P , P - поперечное волновое число для магнитных волн внутри и вне тоннеля соответственно;

P ", P - поперечное волновое число для электрических волн внутри и вне тоннеля соответственно;

K - фазовый множитель;

у , Y - постоянные распространения магнитных и электрических волн соответственно.

С учетом принятия бесконечно большого значения проводимости окружающей горной породы и с учетом полного заполнения тоннеля воздухом (без учета аварийных ситуаций - обвала), постоянная распространения определяется так:

L^2п \2   b ^m м \2

Y = . । (--- ) — (---- ) , где а - радиус тоннеля.

λа

При этом Б_ом = P • a , где P - поперечное волновое число; m = 1, 2, ....

В реальных условиях стенки тоннеля имеют конечную проводимость и, следовательно, уравнения для определения поперечного волнового числа усложняются.

Используем вектор Пойнтинга, который характеризует плотность потока энергии, протекающего через поверхность S в единицу времени. Допустим, что внутрь тоннеля помещен точечный диполь, колеблющийся по гармоническому закону. При этом плотность потока мощности:

П = |Е х Н |.

Вектор Пойнтинга направлен перпендикулярно плоскости E , H . В данном случае вектор П направлен по оси z , а векторы E , H лежат в плоскости x, у . В цилиндрической системе координат проекции вектора Пойнтинга определяются:

П р = Е ф Н_z — E z Н ф ;

П ф = E z Н р — Е р Н z ;

П = ЕН, — ЕН п, z     р ф     ф р, где р = const - поверхность круглого цилиндра;

ф = const - полуплоскость, проходящая через ось z ;

z = const - плоскость, перпендикулярная оси z .

В результате исследования проекции вектора Пойнтинга на оси, учитывая излучение сигнала по обе стороны от антенны внутри тоннеля, получим следующее выражение для мощности сигнала, передаваемого по тоннелю:

2п

Pa = A2 Re J e1-*d,Jai - Y - P1 - J„(p; p) - e- 'z-A - ^^L*- J,(p;p) e"'z]x 0           0

x [ a - ' c ^{1   1} ■ J , ( P l p ) ■ e ^-z -в ;-⁷-²-J ( ( P ; p ) - e ^Yz ]} -

ω µρ

-a■ J, (P; p) ■ e- z+i ■ в; ■ P; - ■ J, (P; p) ■ e-

ω µ ρ

x { - [ ^{a - —} .j, ( p ; p ) ■ e ^- z + l ^a ^L ■ в ; - j , ( p p. e ^- z _n - p d p . ρ c

Затем выражаем электрические и магнитные составляющие поля внутри тоннеля:

E * = PP a^'f '^J- ( P l p ) ■ e * ^- z ⁺ * * '’

H ^; = ^рв 'в.'^р?-^j- ( p ; p ' ' e i¹ "z ⁺ " * '^;

E, = - Aya • [aL,— .J, ( p; p) • ei- z + L^-PvJ1.. в; -j; ( p; p) • ei- z ] • e™ *; Bρ                  c

E p = Pl • ^{[ a} - • i - • p ; ' , ’Pp ; • p ) e ' ^- z - в ; • ^-YY■ ^; • j , ( p ; p ) e ^- z ] ■ e * * ;

H, = /p p - [ a ; -L c-K^ v ; ( p ; p ) ep* - в; ^--*- . J „ ( p ; p ) e i ^-* ] * ;

B     ω µ              ρ

H p =\hF - [ a ; - ^ K ^ - J ; ( p ; p ) e i ^{- Y} *+ ' -A-p; - -■ - J , < p ;p ) e ^- * ] - e i^-* ■

B   ω µ ρ

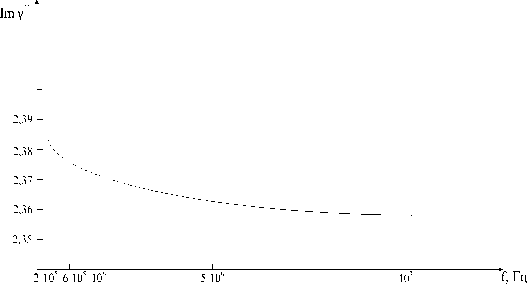
Рис. 1. Частотная зависимость постоянной распространения в условиях «чистой» выработки.

График зависимости постоянной распространения от частоты показан на рисунке 1.

По результатам теоретического исследования процесса распространения радиоволн в подземных тоннелях нефтешахт при отсутствии металлических направляющих элементов можно сделать вывод о том, что наличие конечной проводимости стенок штрека приводит к появлению мнимой составляющей у постоянной распространения γ , что вызовет затухание волны, распространяющейся вдоль оси z . Кроме того, вследствие комплексности γ , граница, определяемая критической длиной волны, будет «размыта». Это означает, что некоторая часть энергии будет распространяться вдоль штрека и в «закритическом» режиме, т.е. λ > λ _кр .