Теоретическое исследование виброакустических характеристик при динамических испытаниях на циклическую прочность

Введение. Вопросы вибро- и шумозащиты всегда были актуальны в машиностроительном производстве. В настоящее время это связано с усилением контроля соблюдения санитарных норм и правил [1] на рабочих местах, что в конечном итоге повышает производительность труда.

Измерения и анализ уровней шума и вибраций согласно [2], проведённые сотрудниками университета на участке динамических испытаний лонжеронов лопастей вертолётов на циклическую прочность ОАО «Роствертол», показали, что проведение мероприятий по шумо- и виброзащите позволит существенно улучшить условия труда. В ходе экспериментов было установлено, что стенд для динамических испытаний лонжеронов лопастей вертолёта выступает и как источник шума, генерируемого колебаниями протяжённого лонжерона, вибровозбудителя и тросов натяжения, и как источник вибраций, возникающих главным образом в результате колебаний опор стенда и передаваемых в цеховое пространство через их основание.

Результаты исследований. Рассмотренная в данной работе математическая модель стенда динамических испытаний лонжеронов лопастей вертолёта является базовой для дальнейших работ по расчёту средств виброзащиты в лаборатории динамических испытаний (ЛДИ) ОАО «Роствертол».

Стенд для динамических испытаний лонжеронов лопастей вертолёта представляет собой сложную конструкцию, состоящую из следующих подсистем (рис. 1):

• •    подсистема опоры со стороны лонжерона I^-,

• •    подсистема опоры со стороны системы натяжения 2,

• •    подсистема тросов натяжения 3;

• •    подсистема лонжерона 4;

• •    подсистема вибровозбудителя 5.

Рис. 1. Структурная схема стенда динамических испытаний лопасти вертолёта

Рассмотрим более подробно структуру стенда. Опоры со стороны лонжерона 1 и со стороны системы натяжения 2, массами Мх и М2 соответственно, соединены с полом цеха упруго- диссипативными связями. Жёсткость сд и диссипация Ь8 связей (/=1,2, j =1,2) в общем случае нелинейно зависят от смещений х, и скоростей х,.

Подсистема натяжения 3 представляет собой систему стальных тросов, с помощью которой осуществляется предварительный натяг лонжерона в стенде. С точки зрения излучения звуковых колебаний эта подсистема представляет собой набор струн. Однако для задачи исследования передачи вибрации в опоры стенда её можно заменить упруго-диссипативной связью, как это сделано на структурной схеме.

Возбудитель колебаний представляет собой два эксцентрика, закреплённых на правом конце лонжерона, и для уменьшения колебаний в продольном направлении вращающихся навстречу друг другу. Вращение производится от электродвигателя постоянного тока (на схеме не показан) с приводом через упругую муфту, практически исключающую передачу колебаний на двигатель.

Эксцентрики имеют форму полуцилиндров, сумма несбалансированных масс эксцентриков равна т , расстояние от несбалансированной массы до оси вращения — г, циклическая частота

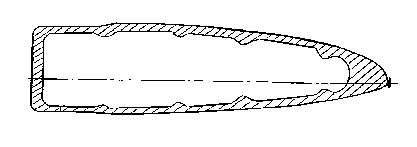
Рис. 2. Сечение лонжерона лопасти вертолёта

вращения оо может регулироваться. Общая масса эксцентриков с системой закрепления равна М₃.

Лонжерон лопасти вертолёта 4 имеет каплевидное сечение (рис. 2). Конструкция стенда позволяет рассматривать лонжерон как балку, шарнирно закреплённую с одного конца. Известно, что такая балка будет иметь л собственных частот и её математическая модель может быть аппроксимирована в виде системы с п сосредоточенными массами и соответствующими частотами и коэффициентами затухания.

Учтены также особенности закрепления опор, которые позволяют представить их как массивные призмы, шарнирно закреплённые одним углом и связанные с основанием упругодиссипативной связью.

Возможность моделирования подсистемы лонжерона 4 (рис. 3) в виде гармонического осциллятора [3] дополнительно можно обосновать резонансным режимом работы стенда динамических испытаний, обеспечиваемым настройкой силы натяжения тросов согласно [4] и подстройкой частоты вращения вибровозбудителя для получения заданной амплитуды колебаний.

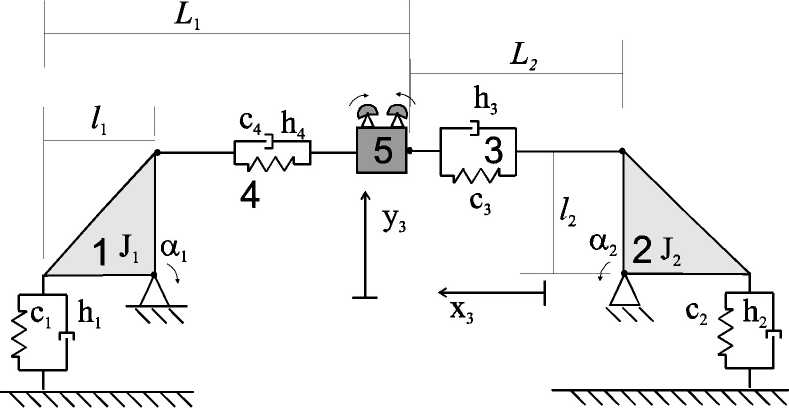
Рис. 3. Структурная схема упрощённой модели системы циклических испытаний лопасти вертолёта

Воспользуемся формализмом Лагранжа 2-го рода [5] для получения уравнений динамики. Кинетическая энергия Т , потенциальная энергия Р, диссипативная функция R и обобщённая сила Q, действующая на систему, имеют следующий вид:

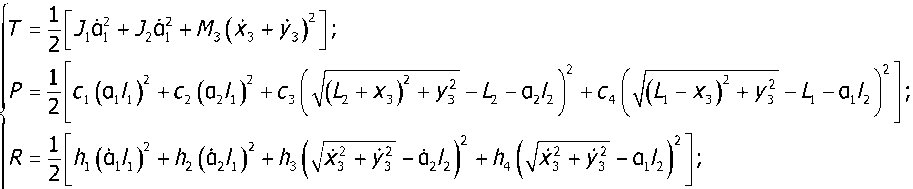
Q_y3 = f(w)sin(wf).

Амплитуда возбуждающей силы зависит от частоты вращения эксцентриков следующим образом [6]:

F (со) = mufr.                                          (2)

Вычисляя частные производные по координатам и импульсам [7] и подставляя их в уравнение Лагранжа, получаем систему уравнений динамики моделируемой системы:

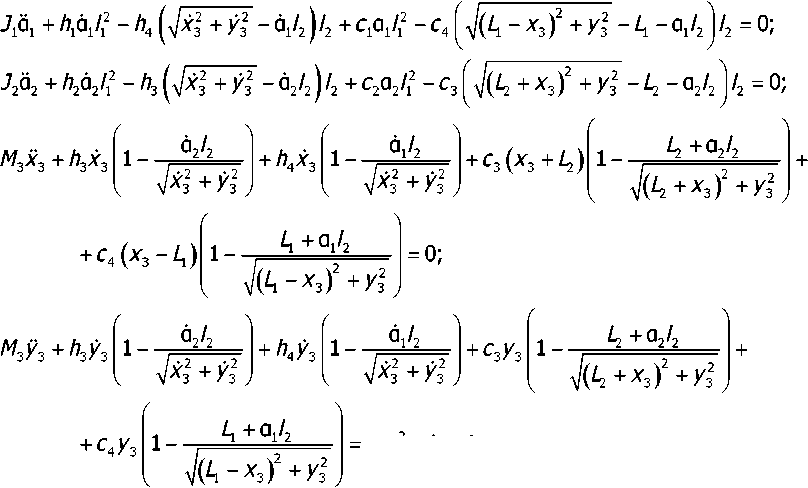
/ттоо г sin oof.

Полученная модель содержит нелинейные составляющие и может быть линеаризована [8] в окрестности нулевых значений х₃, у₂, a_t и а₂. Элементы матрицы частных производных A = ^8fj8x_] ^ имеют вид (для простоты вычислений не учтён множитель -1):

5а,

^ = 0; 502

5^     , .n l /2

__L — h г 4- h г *

H_x!_x f //₄/₂ , (XL

_54_ _ / 2 ^⁴ ( 2^i + 2x₃) /₂ , 54 5x₃"     ^-2Цх_з+х1₊у1 ' 8У₃

^ = 0; 50!

50 2

^Ц-2Цх3+х1+у1

■F-    ^-=0"

3 2'         5a,      '

5^

^ = 0;

5a2

h₄x₃l₇ . 54

5f

UI                  1 ,7

—— — h i 4- h i *

5a2

^4^з4

9f с3(-Ц+хЛ17 ef c,y,L QL h,x,L QL h,y,L

^9хз ^+^Т^у1' ^9Уз ^+х₃^+У1 ' ⁹*з      + yj ' ⁹Уз J^yf

Bf₃ 90!

^4 (*з 4)4     . 5f3 _ _ c3 + x3) /2 _ 5f3 _ _ h^x3l2 , 6f3 _ _ h3x3l2

\Ч ^"Ч^Л3 ^Л3 7 3      ²     л/( Ц + ^3 I + Уз ¹      \^л3 ⁺ 7 3      ² Ч^Л3 ⁺ 7 3

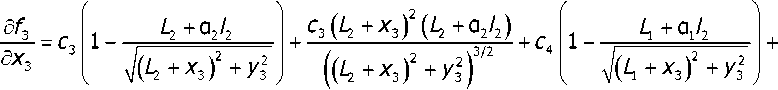
, c3(4+^)2(4+ai4)

((4+^з)2+Уз2)3/2

^ = Сз(М2РЙ^5!^ + 51к125Ж±21!2^

/з ((^+^з)+Уз2)       ((4+^з) +Уз)

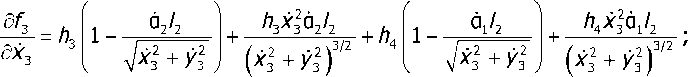
5Л h₃x₃a₂Ly₃ h₄x₃a,Ly₃

U/3 I XZ + VZ 1 I XZ + VZ 1

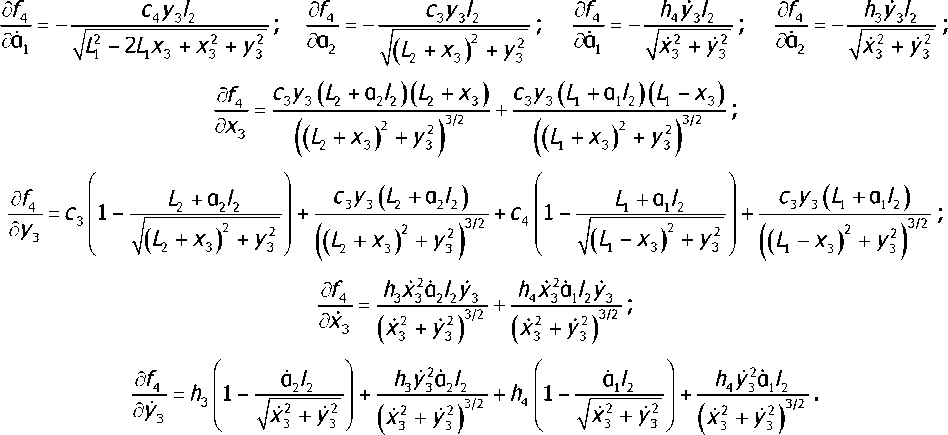
После подстановки значений координат в точке равновесия X*

X —10| 0₂ Oj 0₂ Х₃ у₃ Х₃ У₃< - (О О О О О О 0 Oj (4) получаем матрицу частных производных, соответствующую собственной матрице линеаризованной системы в явном виде:

of

ОХ

Г о 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 Сik ^^sk о hj? +М1 о с4/2 о h^k h.k Л Л Л Л Л о с3Ц + с3/2 о h2l^ + hj^ С / о /)3/2 />3/2 Л J. Л Л Л 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 ^4 к ^зк h.k /)3/2 С3 + С4 о h3 +h4 о М. Мз Мз Мз Мз m3 0 0 м Мз ^зк Мз 0 0 0 _/73+/74 м3 J и система уравнений динамики может быть записана в виде: ^Х = АХ+Ви; Ik = сх.

Экспериментальные измерения, проведённые на участке динамических испытаний, показали, что амплитуды вибраций во всех частотных диапазонах на опорах стенда динамических испытаний на 15...20 дБ меньше амплитуд колебаний на конце лонжерона, закреплённого на вибровозбудителе. То есть амплитуды колебаний опор на несколько порядков меньше амплитуды колебаний вибровозбудителя. Исходя из этого, можно осуществить дальнейшее упрощение модели (3) стенда динамических испытаний, рассматривая его с точки зрения анализа формы возникающих колебаний как упругую подсистему, прикреплённую к неподвижным опорам (рис. 4, а), а с точки зрения передачи вибрации через опоры — как упругие подсистемы опор, на которые действует внешняя сила, характеристики которой определяются из предыдущей подсистемы (рис. 4, б).

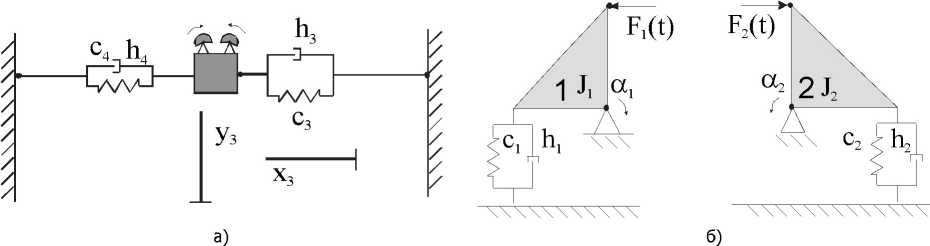
Рис. 4. Декомпозиция динамической модели рис. 3 на подсистемы: а — вибровозбудителя; б — опор

Таблица 1

Режимы динамических испытаний лонжеронов

Испытываемый участок	Статическая нагрузка	Переменная нагрузка сясп, МПа				Частота колебаний образца, Гц
Средний участок с двумя секциями каркаса и в плоскости тяги	ор =88,2 МПа ((2 = 1176 Н)	54	68,6	88		41	42	42
Концевой участок с двумя секциями каркаса в плоскости тяги	ор =58,8 МПа ((2= 1176 Н)	35	54	68,6	88	38	38	40	42
Концевой участок с двумя секциями каркаса в плоскости тяги	ор =58,8 МПа	54	68,6	88		38	40	42

Соответствующие системы уравнений, описывающие динамические свойства полученных подсистем, представлены ниже. Для подсистемы вибровозбудителя:

\М₃х₃ + (с₃ + с₄ )х₃ + (h₃ + ЬЛх₃ + г,у₃ = 0;

\М₃у₃ + (Л₃ + ^4 ) Уз = Л™²/"^Sin ^^ ■

Для подсистем опор:

J^+hJ^+c^a^kF^ty

J2o2 + Ь2Уа2 +с2^а2 = !2F2 ^ty

Соответственно силы F_x (t) и F₂ (Г) получаются в линейном приближении из стационарных решений системы уравнений (7) по формулам:

(Ю)

(И)

\р^ = с3х3^ + Ь3х3(1у

Численный расчёт удобно проводить, представив уравнения (7) — (9) в форме Коши:

-(М^+еа)/^;

z₄ =(-(Л₃ +h₄^z₄ + mto²rsmtot^M₃, где z_x = х₃, z₂ = х₃, z₃ = у₃, z₄ = у₃;

5 * ^6

7 - ^8

где z₅ Qi, z₆ Qi, z? Оу, Zg g₂

Параметры модели стенда динамических испытаний

Таблица 2

Обозначение	Значение	Размерность	Пояснения
G	5-IO6	Н/м	Жёсткость опоры co стороны лонжерона
С2	107	H/m	Жёсткость конструкции со стороны тросов натяжения
Сз	2,2-Ю4	H/m	Приведённая жёсткость системы тросов натяжения
<4	3,5-IO5	H/m	Приведённая жёсткость лонжерона
hi	1000	H-c/m	Диссипация в опоре со стороны лонжерона
hz	1000	H-c/m	Диссипация в опоре со стороны тросов натяжения
hi	10	H-c/m	Приведённая диссипация в системе тросов натяжения
hi	10	H-c/m	Приведённая диссипация в лонжероне
А	0,5	M	Длина образующей опоры
6	0,4	M	Высота образующей опоры
h	2	M	Длина лонжерона
Lz	1,5	M	Длина системы тросов
3i	1	H'M2	Момент инерции опоры со стороны лонжерона
3z	1	H'M2	Момент инерции опоры со стороны тросов натяжения
Мз	10	КГ	Масса подсистемы возбудителя
m	0,4	КГ	Масса груза вибровозбудителя
r	0,05	M	Радиус эксцентриситета груза вибровозбудителя

а)

Время, с

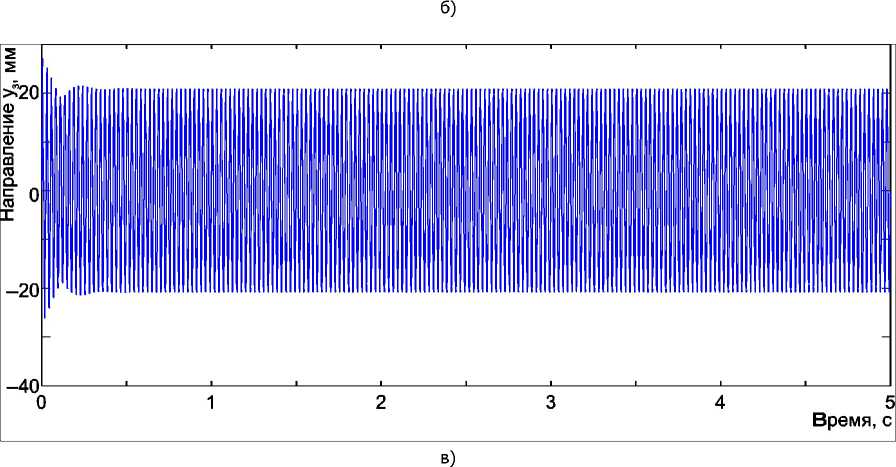
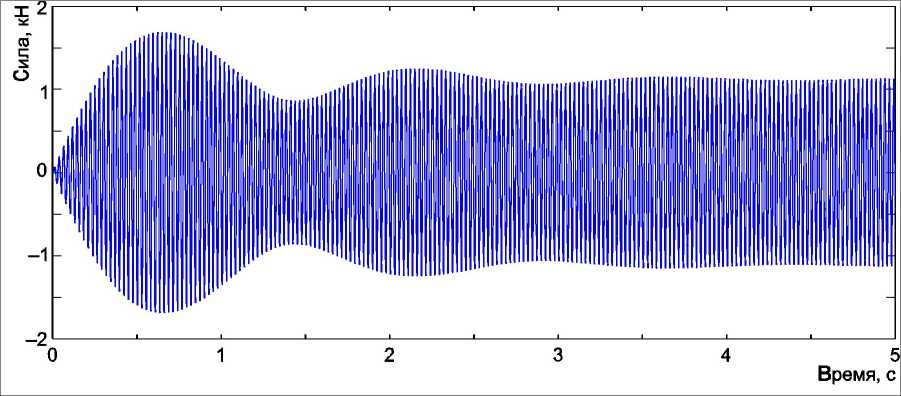
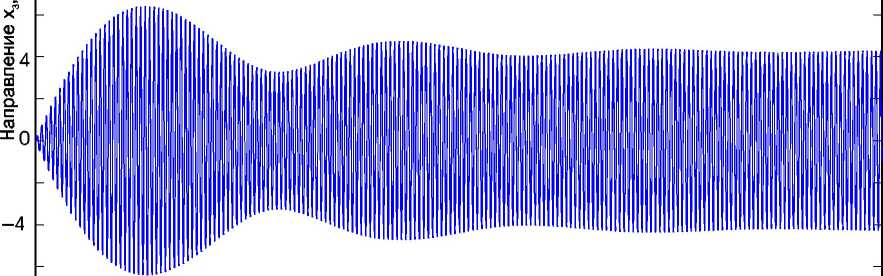
Рис. 5. Результаты моделирования работы стенда динамических испытаний лонжеронов лопастей вертолётов: а — смещение в горизонтальном направлении; б — смещение в вертикальном направлении; в — переменная составляющая растягивающей силы, действующей на лонжерон

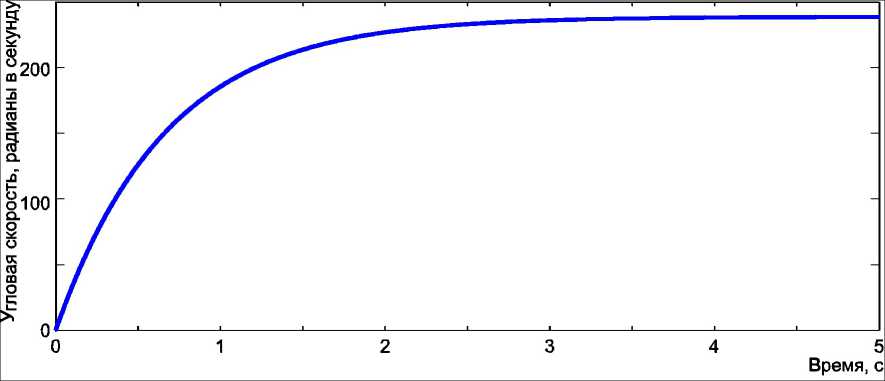
Рис. 6. Зависимость частоты вращения вибровозбудителя от времени при плавном увеличении частоты вращения

Таким образом, определение коэффициента передачи вибрации через опоры стенда динамических испытаний производится в два этапа: на первом этапе определяется установившееся решение системы х(Г) х^ (7), а на втором этапе полученные установившиеся решения подставляются в выражение для внешних сил уравнений (8) и (9), для которых в свою очередь так же находятся установившиеся решения o_t (t), с^ (t), о₂ (t), о₂ (t).

Моделирование динамики стенда циклических испытаний лонжерона лопасти вертолёта. В соответствии с программой испытаний лопасти несущего винта определены условия и режимы испытания лонжеронов лопастей несущего винта вертолётов. Для рассматриваемого в данной работе стенда динамических испытаний, на котором испытываются средние и концевые участки лонжерона, определены следующие условия испытаний (табл. 1).

Результаты предварительных измерений и анализа конструкции стенда динамических испытаний позволили оценить значения постоянных с, модели стенда. Они приведены в табл. 2.

Результаты моделирования, выполненные на основе [9], приведены на рис. 5. Как показало моделирование, при быстром выводе оборотов двигателя вибровозбудителя в зону резонанса возможны колебания амплитуды упругих сил, действующих на лонжерон, что может привести к его повреждению. По этой причине при запуске стенда динамических испытаний применяется плавный выход в зону резонанса, с относительно медленным повышением частоты вращения вибровозбудителя (рис. 6).

Зависимость возбуждающей силы в этом случае может быть описана формулой

F (t, го) = т (со (1 - e^t,T ))² г sin (со (1 - e^t,T ) f), (14) учитывающей постепенное возрастание как частоты, так и амплитуды колебаний возбуждающей силы. Зависимость возбуждающей силы от времени приведена на рис. 7, а, а соответствующие графики изменения координат состояния моделируемой системы — на рис. 7, б, в.

Заключение. Приведённые в работе результаты математического моделирования позволяют сделать вывод о работоспособности разработанных моделей стенда динамических испытаний лонжеронов лопастей вертолётов и их применимости для расчёта характеристик источников шума и вибрации. Результаты моделирования показали соответствие экспериментальным измерениям как по качественному поведению системы, так и по количественным показателям — амплитудам колебаний и величинам сил.

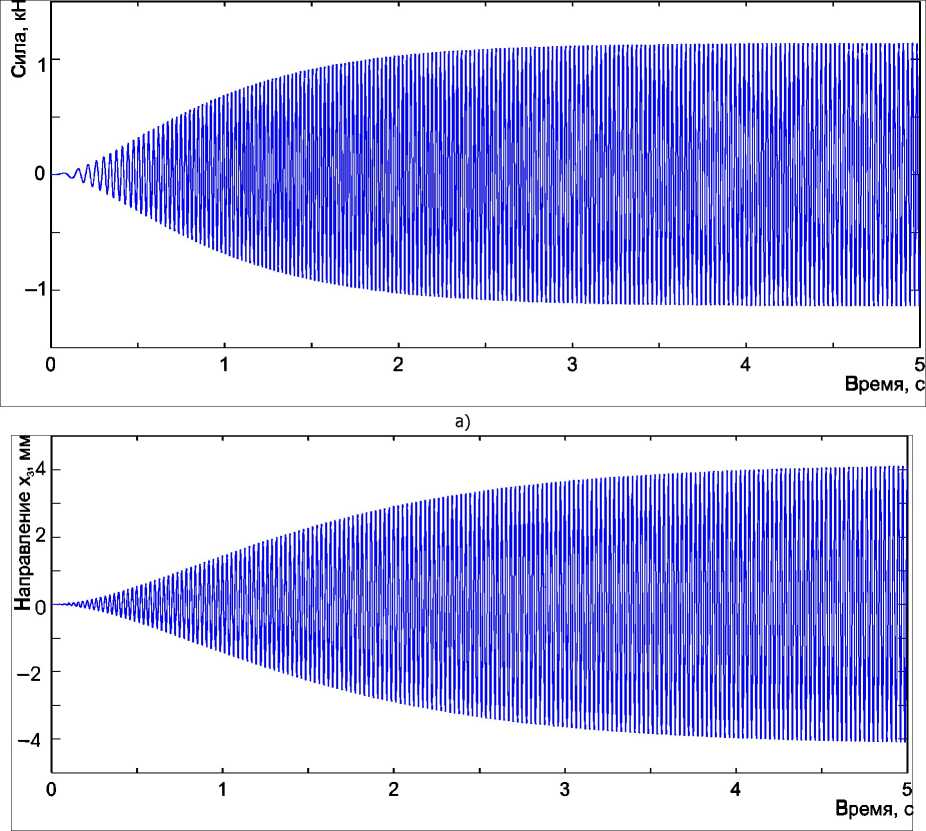
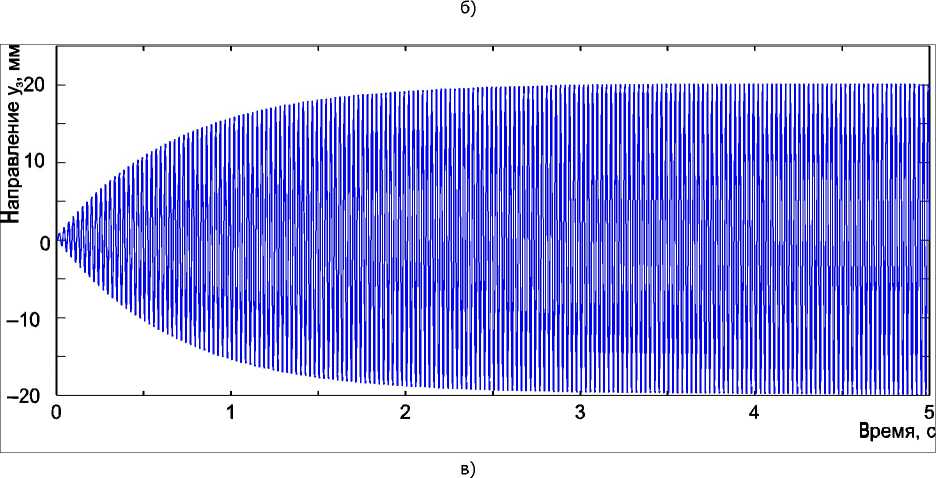
Рис. 7. Результаты моделирования работы стенда динамических испытаний лонжеронов лопастей вертолётов при плавном увеличении частоты вращения: а — смещение в горизонтальном направлении; б — смещение в вертикальном направлении; в — переменная составляющая растягивающей силы, действующей на лонжерон