Теоретическое моделирование взаимодействия индентора атомно-силового микроскопа с жидкой нанопленкой на поверхности образца

микроскопа возможна в одном из трех основных режимов: бесконтактном, контактном и полу-контактном [2]. Бесконтактная атомно-силовая микроскопия основана на использовании вибрационной методики и применяется только для измерения топографии поверхности. В контактном режиме острие зонда находится в непосредственном соприкосновении с поверхностью, при этом силы притяжения и отталкивания со стороны образца уравновешиваются силой упругости кантилевера. В полуконтактном режиме острие зонда АСМ совершает колебания по заданному закону и слегка стучит по поверхности образца. Последние два режима представляют наибольший интерес, так как они позволяют получать данные не только о рельефе поверхности, но и об ее механических свойствах.

Основным элементом АСМ является кантилевер в виде консольной стальной балки с кремниевым щупом на свободном конце. Как правило, этот щуп (зонд) имеет форму конуса со скругленной вершиной. Длина балки составляет около 100-200 мкм, высота конуса 1-3 мкм. Радиус вершины зонда у современных кантилеверов варьируется от 1 до 50 нанометров. В процессе работы зонд АСМ сканирует выбранную поверхность образца. Получаемые при этом экспериментальные данные представляют собой зависимости между координатами точек сканирования, силой реакции, действующей на зонд, глубиной проникновения вершины зонда в исследуемый материал и вертикальным смещением точки крепления консоли зонда. Эти результаты сами по себе малоинформативны, поэтому требуется их дальнейшая теоретическая расшифровка с привлечением различных физических и механических моделей. В таких моделях могут учитываться не только механические силы, но и ряд других факторов, влияние которых на наноуровне может быть очень существенным. Это межмолекулярное взаимодействие Ван-дер-Ваальса, силы поверхностного натяжения, связанные с искривлением поверхности материала в зоне контакта, капиллярные силы [3-9]. В данной статье авторами рассматривается влияние капиллярных сил на зонд АСМ.

В обычных атмосферных условиях на поверхности исследуемого образца образуется адсорбированный слой жидкости, что приводит к усложнению взаимодействия зонд – образец [1012], потому что на наномасштабном уровне большое значение приобретают силы поверхностного натяжения. Процессу образования адсорбированных пленок, изучению их свойств и степени влияния на силу взаимодействия с зондом, посвящено большое количество экспериментальных работ [13-17] и предложены модели для описания получаемых результатов. При контакте зонда АСМ с пленкой жидкости на поверхности образца происходит образование мениска на границе жидкости и на зонд начинают действовать капиллярные силы. В настоящее время предложено аналитическое и численное описание формы мениска и приведена оценка возникающей силы в зависимости от формы контактирующих поверхностей и расстояния между ними [18-19]. Известны работы, посвященные уравнению движения кантилевера с учетом капиллярных сил, сил Ван-дер-Ваальса, относительной влажности и расстояния между зондом и образцом [20-21]. Несмотря на достигнутые успехи в моделировании явлений взаимодействия зонда АСМ с жидкостью, это описание можно существенно уточнить за счет учета ранее не рассматриваемых факторов. По нашему мнению, следует определить геометрию поверхности жидкости около зонда АСМ без использования упрощающих предположений относительно геометрии поверхности, ее кривизны, не пренебрегая силой тяжести. В результате получится более точная информация о том, на какую высоту поднимается жидкость на границе зонда и какие при этом возникают капиллярные силы. Соответствующие расчеты производятся в данной статье.

Постановка задачи и ее решение. Для описания зависимости между межфазной границей жидкости и давлением жидкости авторы использовали следующее уравнение:

a u" u ' i = ---:—24" +--

V1 + (u *)2 11 + (u')     r J где α – коэффициент поверхностного натяжения на границе раздела фаз, p – давление жидкости, u – перемещение точек границы жидкости вдоль вертикальной оси z, r – координата рассматриваемой точки границы жидкости в цилиндрических координатах, u' и u'' – первая и вторая производные по координате r. Это уравнение аналогично записи уравнения Юнга-Лапласа для случая осесимметричного мениска при контакте сферы и плоскости, предложенного в статье [22]. Orr et.all провели оценку формы менисков и значений их кривизн, предполагая, что число Бонда очень мало и эффектом гравитации можно пренебречь. В такой постановке уравнение (1) имеет аналитическое решение. Также авторы провели оценку влияния гравитационных сил на капиллярный эффект, решив это уравнение численно, и сделали вывод, что ими можно пренебречь ввиду малости. Эти результаты были получены для макромасштабных размеров зонда – миллиметры и более (публикация 1975 г.), когда еще не исследовались эффекты наномасштабного уровня, поэтому вклад силы тяжести был недооценен. Наши расчеты показали, что когда речь идет о нанометрах, то силой тяжести пренебрегать нельзя. На рис. 1 представлены решения, полученные с учетом (сплошная линия) и без учета гравитационных сил (штриховая линия). Видно, что учет сил тяжести приводит к более низкому профилю жидкости и переход к невозмущенной жидкости происходит плавно на расстоянии от 1 мм до 1 см, что больше соответствует действительности. Значит, на наномас-штабном уровне силы тяжести необходимо учитывать.

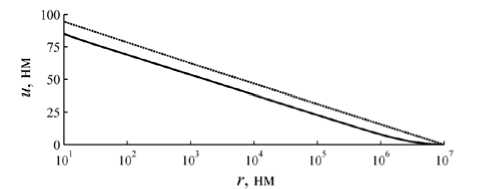
Рис. 1. Профиль жидкости около зонда, рассчитанный с учетом давления жидкости (сплошная линия) и в предположении, что гравитационной силой можно пренебречь (пунктирная линия)

Найдем капиллярную силу, действующую на зонд АСМ, используя уравнение (1), с учетом гравитационной составляющей. Рассмотрим внедрение кремниевого конического зонда с углом раскрытия конуса 40º и радиусом скругления вершины R= 10 нм в жидкость. Считаем, что на поверхности образца находится дистиллированная вода при температуре окружающей среды 20ºС. В этом случае плотность воды ρ =998 кг/м³, коэффициент поверхностного натяжения α =72,8∙10³ Н/м. Ускорение свободного падения g =9,8 м/с². Равновесное значение краевого угла смачивания поверхности кремния дистиллированной водой $ примем равным 68,1° [23-24]. Давление, действующее на зонд со стороны жидкости

Р = -Р gu

.

Используя выражения (1) и (2), получаем уравнение

u

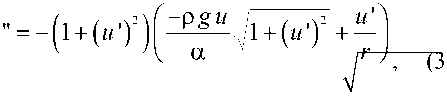
которое необходимо решить, чтобы найти пере-

мещение точек границы жидкости в осесимметричной задаче внедрения зонда в воду, то есть функцию u . Уравнение (3) решали методом Рунге-Кутта четвертого порядка. В результате была определена геометрия границы межфазной жидкости возле зонда. Она показана на рис. 2. Видно, что искривление границы жидкости около зонда распространяется на величину, существенно превышающую радиус зонда АСМ (до 1 см), т.е. капиллярная сила, вызванная искривлением поверхности, вносит существенный вклад во взаимодействие зонда и исследуемого образца.

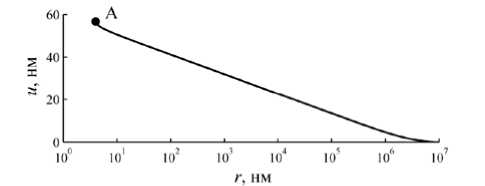
Рис. 2. Профиль жидкости около зонда, рассчитанный с учетом давления жидкости (сплошная линия) и в предположении, что гравитационной силой можно пренебречь (пунктирная линия)

Найдем силу поверхностного натяжения F , которая действует на границе раздела трех фаз.

Сила эта является втягивающей (направлена вниз) и значение ее вычисляется по формуле:

F = 2 п r a cos ( ф )

где ф - угол между направлением силы F и вертикальной осью z . На рис. 3 показана зависимость силы поверхностного натяжения от величины H , где H – расстояние между кончиком зонда и уровнем невозмущенной поверхности жидкости.

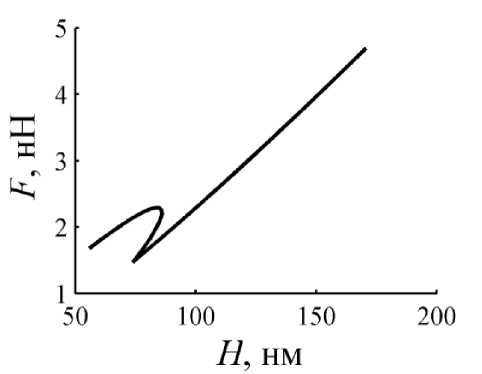
Рис. 3. Профиль жидкости около зонда, рассчитанный с учетом давления жидкости (сплошная линия) и в предположении, что гравитационной силой можно пренебречь (пунктирная линия)

Видно, что разным значениям параметра H соответствует одно значение силы F . Это происходит в начале участке рассматриваемой кривой и соответствует случаю, когда точка А (точка касания мениска жидкости и зонда) лежит на сферической части зонда. Получается, что данный участок зависимости является неустойчивым. В рамках данной постановки задачи невозможно оценить, какая из ветвей является устойчивой. Авторы предполагают, что неустойчивость объясняется тем, что в момент касания зонда и жидкости, зонд должен сразу нырять на большую величину порядка микрон. В данном случае необходимо рассмотреть более точную постановку задачи и ввести в рассмотрение и другие силы, например, силу Ван-дер-Ваальса, силy упругости кантилевера.

Выводы: рассмотрена осесимметричная задача погружения конического зонда со скруглением в жидкость. Получен профиль мениска на наномасштабном уровне с учетом действия силы тяжести. Установлено, что на наномас-штабном уровне нельзя пренебрегать силой тяжести. Показано, что искажение поверхности жидкости распространяется на большое расстояние. Вертикальный подъем жидкости на десятки нанометров вызывает искривление профиля мениска на расстоянии до одного сантиметра. Это особенность наномасштабного уровня. Рассмотрено действие капиллярных сил на зонд АСМ при контакте с жидкостью. Показано, что на наномасштабном уровне сила поверхностного натяжения составляет порядка нескольких наноньютонов. При нахождении зависимости силы поверхностного натяжения от расстояния между кончиком зонда и невозмущенной поверхностью, была выявлена область неустойчивости при переходе со сферической части зонда на коническую.

Работа выполнена при финансовой поддержке РФФИ грант № 11–08–96001_р_урал_а, грант № 14-01-96002_р_урал_а, программы РАН № 12–Т–1–1004 и Министерства образования и науки Пермского края (соглашение № С–26/627).