Теоретическое обоснование алгоритма определения моментов от вращающихся масс воздушного судна

В математических моделях (ММ) динамики полета модели предстоит количественная оценка влияния воздушного судна (ВС) моменты, (гироскопические моменты и моменты, зависящие от изменения угловой скорости подвижных частей), вызванные вращением с большой угловой скоростью подвижных частей двигателей, учитываются для поршневых однодвигательных ВС. Имеется полная ММ, описывающая вращательное движение системы «самолет + винт» [1]. В то же время в ММ многодвигательных ВС, в том числе магистральных ВС типа Ту-204, Ил-96-300 и др., упомянутые моменты, как правило, не учитываются [2; 3]. Общий подход к определению гироскопических моментов от вращающихся масс ВС рассмотрен в ряде работ [4–6]. Отметим, что вопросы движения космических аппаратов с учетом вращающихся масс детально разработаны в многочисленных публикациях, например в монографии Ю. П. Артюкина [7].

Настоящие результаты являются дальнейшим развитием исследований [8; 9].

Постановка задачи. Ставится задача теоретического обоснования математической модели динамики полета ВС, в которой будет учтен момент от вращающихся масс работающих двигателей. Затем на основании применения уточненной математической момента от вращающихся масс на динамику движения ВС относительно центра масс и в случае его существенного влияния выработка рекомендаций по управлению движением воздушного судна.

При решении задачи считаем, что угловая скорость вращения подвижной части двигателя Ω в общем случае величина переменная Ω = Ω ( t ).

Математическая модель вращательного движения воздушного судна. Основное уравнение динамики движения объекта (твердого тела) относительно центра масс в общем случае имеет вид

d to

J--+ tox J-to=M ,              (1)

dt где J - тензор инерции тела; to - вектор абсолютной угловой скорости вращения тела относительно инерциального пространства; ^-^ - производная по вре-dt мени вектора абсолютной угловой скорости; M – вектор суммарного момента внешних сил, действующих на тело.

Применяя формулу (1) к воздушному судну, имеющему вращающиеся части (роторы) (см. рисунок), получим выражение для вектора момента ( M _{вр Σ} ):

M=-(J⋅dΩ+ω×J⋅Ω+Ω×J⋅ω+Ω×J⋅Ω), (2) вр Σ  pdt ppp где Jp – тензор инерции ротора относительно начала связанной с ВС системы координат,

Ω=Ωi1,(3)

где i ₁ – орт, направленный по продольной оси ВС.

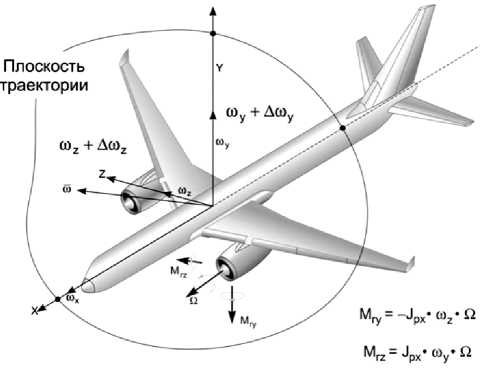
Схема пространственной ориентации ВС с массой, вращающейся с угловой скоростью Ω

Учитывая (3), имеем dQ = Q ®x i1 + Q i1 .(4)

Подставляя (3) и (4) в (2), получим выражение для гироскопического момента ( М _{Г Σ} ):

МГΣ = -Ω (Jp⋅ω×i1+ω×Jp⋅i1+i1×Jp⋅ω).(5)

В (2) имеем член Ω× J_р ⋅Ω , после соответствующих вычислений можно показать, что

Ω× J_р ⋅Ω = 0.

Момент ( M _Ω ), вызванный изменением угловой скорости подвижных частей, равен

I I                                                                                        __________ •

M Ω = - J р ⋅ i 1 Ω .

Рассмотрим возможность ориентации вращающихся масс по отношению к связанной системе координат, заданной ортами e . В этом случае производная по времени вектора

Ω=Ωe, dΩ

=Ω ω × e +Ω e . dt

(6а)

(6б)

Подставляя (6 а) и (6 б) в (5) и (6), получим

МГΣ = -Ω(Jp⋅ω×e+ω×Jp⋅e+e×Jp⋅ω).(5а)

MΩ = -Jр⋅eΩ.(6в)

Суммарный момент от вращающихся масс равен

MврΣ= МГΣ + MΩ .(7)

Представим векторы М _{Г Σ} и M _Ω в координатной форме.

Вектор суммарного гироскопического момента М _{Г Σ} удобно представить в виде двух слагаемых:

М _{Г Σ} = M _Г +Δ M _Г,             (8)

где M _Г – вектор гироскопического момента в предположении, что центробежные моменты инерции ротора равны нулю; Δ M _Г – составляющая вектора гироскопического момента, вызванная центробежными моментами ротора относительно центра масс ВС.

При совершении в (5) соответствующих вычислений получены следующие выражения для компонентов гироскопического момента от i -го работающего двигателя ВС:

MiГx = 0,(9)

MiГy=(-Jiрx-Jiрy+Jiрz)⋅ωz⋅Ω,(10)

MiГz=(Jiрx-Jiрy+Jiрz)⋅ωy⋅Ω,(11)

ΔMiГx=-Ω(Jiрxzωy-Jiрxyωz),(12)

ΔMiГy=-ΩJiрyz ωy ,(13)

ΔMiГz=ΩJiрyz ωz ,(14)

где M _{Г Σ x} , M _{Г Σ y} , M _{Г Σ z} – компоненты вектора M _{Г Σ} гироскопического момента в связанной с ВС системе координат; ω y , ω z – угловые скорости рыскания и тангажа соответственно; J_iрx , J_iрy , J_iрz – моменты инерции ротора i -го двигателя относительно связанных с ВС осей координат; J_iрxy , J_iрxz , J_iрyz – центробежные моменты инерции ротора i -го двигателя.

Для n работающих двигателей имеем

n

MΣГx=ΣMiГΣx,(15)

i = 1

n

MΣГy=ΣMiГΣy,(16)

i = 1

n

MΣГz=ΣMiГΣz.(17)

i = 1

Вектор M _Ω также представим в виде двух слагаемых:

MΩ = MΩ0 + Δ MΩ ,(18)

где M Ω0 – вектор момента, вызванного изменением угловой скорости Ω , в предположении, что центробежные моменты инерции ротора равны нулю; Δ M Ω – составляющая вектора M Ω , вызванная центробежными моментами ротора относительно центра масс ВС;

MiΩ0x = –J iрx ⋅Ω,(19)

MiΩ0y = 0,(20)

MiΩ0z = 0,(21)

ΔMiΩx= 0,(22)

ΔMiΩy= Jiрxy ⋅Ω ,(23)

ΔMiΩz=Jiрxz ⋅Ω .(24)

Для n работающих двигателей имеем n

MΣΩx =ΣMiΩx,(25)

i = 1

n

MΣΩy = ΣMiΩy,(26)

i = 1 n

MΣΩz =ΣMiΩz,(27)

i = 1

MврΣx=MΣГx+MΣΩx ,(28)

MврΣy=MΣГy+MΣΩy,(29)

Mвр Σz = MΣГz + MΣΩz .(30)

Моменты инерции ротора двигателя относительно связанных с ВС осей координат J , J , J , J , рx     рy     рz     рxy

J_рxz , J_рyz можно представить как

Jрx =Jсрx+mр(y2р+z2р),(31)

Jрy =Jсру+mр(xр+zр),(32)

Jрz =Jсрz+mр(x2р+y2р),(33)

Jрxy =Jсрxy+mрxр⋅yр,(34)

J рxz =J р zx +mрxр⋅zр,(35)

Jрyz =Jсрyz+mрyр⋅zр,(36)

где J^с_рx , J^с_рy , J^с_рz , J ^с_рxy , J^с_рxz , J ^с_рyz – собственные моменты инерции ротора двигателя; собственные центробежные моменты ротора двигателя равны нулю; x_р , y_р , z_р – координаты центра масс ротора в связанной с ВС системе координат с началом в центре масс ВС; m _р – масса ротора двигателя.

Исходные данные для вычисления моментов, вызванных вращением масс ВС: компоненты угловой скорости ВС ω x , ω y , ω z ; собственные моменты инерции ротора двигателя J^с_рx , J^с_рy , J^с_рz ; x_р y_р z_р – координаты центра масс ротора в связанной с ВС системе координат с началом в центре масс ВС; m _р – масса ротора двигателя; Ω – угловая скорость вращения ротора двигателя; Ω – производная угловой скорости ротора двигателя по времени.

После подстановки компонентов соответствующих гироскопических моментов и моментов, вызванных изменением угловой скорости подвижных частей, в выражения для имеющейся математической модели ВС [2] получим:

MxΣ = (mxΣ ⋅q ⋅S⋅L+M +M xpx I x ∅+MврΣx) , (37) MyΣ = (myΣ ⋅q ⋅S⋅L+Myp+My∅+MврΣy) Iy                        , (38) MzΣ = (mzΣ ⋅q⋅ S⋅b+Mzp+Mz +MврΣz) (39) Iz , где mxΣ ⋅q⋅ S⋅L, m yΣ q⋅S⋅L, mzΣ ⋅q⋅ S⋅b – аэродина- мические моменты ВС; M , M ; M – моменты xp yp zp от тяги двигателей ВС; Mx ∅ , My ∅ , Mz ∅ – моменты от шасси при движении ВС по взлетно-посадочной полосе.

С применением предложенного алгоритма в уточненной ММ динамики полета ВС можно оценить влияние суммарного момента от вращающихся масс на динамику движения, например, двухдвигательного воздушного судна при отказе одного из них. При решении задачи проводится математическое моделирование вариантов полета ВС без учета и с учетом в ММ момента M _{вр Σ} .

Приведенный алгоритм вычисления компонентов суммарного момента от вращающихся масс и методику учета этого момента в общих уравнениях динамики движения ВС можно распространить на общий случай движущегося объекта (летательного аппарата (ЛА), вертолета, космического ЛА), имеющего вращающиеся массы с векторами оси вращения, направленными не только по его продольной оси, но и по направлениям поперечных осей с ортами i ₂ , i ₃ . Рассмотрена также возможность ориентации вращающихся масс по отношению к связанной системе координат, которая задается ортами e .

Результаты исследований могут быть использованы при разработке алгоритмов расчета на ЭВМ параметров движения летательных аппаратов, имеющих вращающиеся части, совершенствовании математических моделей ЛА и в задачах математического моделирования функционирования систем управления, авиационных тренажеров, робототехнических комплексов и других устройств ЛА. Дальнейшая задача состоит в количественной оценке влияния моментов от вращающихся масс на динамику движения ВС.