Теоретическое обоснование эффекта Мейснера

Эффект Мейснера по определению заключается в том, что магнитное поле полностью вытесняется из объема сверхпроводника [1]. Принято считать, что этот эффект служит экспериментальным доказательством того, что существует принципиальное отличие внутренней структуры сверхпроводника от обычного проводника. Далее будет доказано, что этот эффект – следствие больших токов, а не специфики материала.

Прежде всего рассмотрим великолепный эксперимент [2]. Сверхпроводящий диск висит над плоским кольцом магнитов и движется вдоль этого кольца, как по рельсам, если экспериментатор его слегка толкнет - см. рис. 1. Свехпроводящий диск висит и под кольцом магнитов, а также удерживается рядом с наклоненным магнитом под любым углом наклона этого магнита - см. рис. 2. Совершенно очевидно, что ни отталкиванием, ни притяжением диска и магнита невозможно объяснить этот эксперимент. Представление о магнитном выталкивании не помогает найти объяснение. Есть эффект, но его общепринятое определение придумано под придуманное объяснение. Это то, что называется подгонкой под ответ.

Рис. 1.

Рис. 2.

Таким образом, эффект Мейснера следует определить как положение проводника рядом с магнитом без их соприкосновения, устойчивое и независимое от ориентации магнита и относительной скорости движения проводника.

Это означает, что требует объяснения не только факт отталкивания, но и факт притяжения магнита и проводника . Гравитационная сила не может быть объяснением для притяжения проводника снизу и сбоку. Поэтому далее мы будем пренебрегать силой притяжения.

2.    Токопроводный диск рядом с магнитом

Далее будем рассматривать проводник в виде диска. Рассмотрим дисковый соленоид с током, расположенный рядом магнитом так, что ось соленоида перпендикулярна плоскости торца магнита. На каждый элемент проводника действует сила Лоренца, как векторное произведение элемента тока и индукции магнита.

Горизонтальные проекции сил Лоренца суммируются. Читатель может убедиться, что сумма этих сил становится равной нулю, когда эти силы расположены симметричного относительно оси соленоида. Такое положение создается, когда ось соленоида совпадает с осью магнита. Следовательно, силы Лоренца располагают соленоид так, чтобы его ось совпадала с осью магнита . Поэтому далее мы будем рассматривать только осевые силы притяжения или отталкивания.

В приложении доказывается, что в проводящем диске под действием постоянного внешнего магнитного поля

• •    возникает постоянный ток,

• •    этот ток в цилиндрических координатах распространяется по радиусу, по окружности и вдоль оси диска,

• •    ток возникает несмотря на то, что диск не является замкнутым проводником ни по радиусу, ни по оси,

• •    линии тока имеют спиральную структуру,

• •    по окружности ток может вращаться в ту или иную сторону, либо вообще не вращаться.

Таким образом, можно говорить о том, что проводящий диск в поле постоянного магнита представляет собой соленоид. Этот соленоид взаимодействует с магнитом, т.е. магнит создает соленоид, который с взаимодействует с этим магнитом.

Кольцевые токи, возникающие в диске, создают осевую магнитную напряженность, направленную против магнитной напряженности магнита и поэтому диск отталкивается от магнита. Это соответствует правилу Ленца. По мере увеличения расстояния между диском и магнитом внешняя напряженность, действующая на

Доклады независимых авторов 2020 выпуск 51 диск, уменьшается и уменьшается величина токов. Прежде всего уменьшается величина кольцевых токов и уменьшается сила отталкивания диска от магнита. В некоторый момент кольцевые токи становятся равными нулю. Если диск продолжает удалятся от магнита, то вновь появляются кольцевые токи, направленные в противоположную сторону, и диск притягивается к магниту. Таким образом, положение диска в точке нулевого кольцевого тока является устойчивым .

Отсюда следует, что проводник, расположенный рядом с постоянным магнитом, может демонстрировать эффект Мейснера. Этот эффект будет тем большим, чем меньше сопротивление проводника. Не удивительно, что этот эффект был обнаружен в экспериментах со сверхпроводниками. Но этот эффект НЕ является следствием сверхпроводимости.

Приложение. Структура постоянного тока.

В [1, глава 5] показано, что в проводе постоянного тока распределение плотностей тока / и магнитных напряженностей Н в описываеться уравнениями Максвелла, которые в этом случае имеют вид:

rot(H) = 0 ,	(1)
div(H) = 0 .	(2)
rot(/) = 0 ,	(3)
divQ) = 0,	(4)
При моделировании будем использовать цилиндрические
координаты г, ф, z . Тогда эти уравнения примут вид:
Нг дНт 1 ЭНж дН,
— +   + 1 •    +   = 0 ,	(5)
г     дг г дф    дг
1 ^ ЭНг _ д- ф = _ г дф    дг    Гг’	(б)
дНт _ дНг = дг дг = 'ф,	(7)
Н ф , ЭН ф _ 1 ЭН г = . г     дг    г дф " z’	(8)
- + дг + ^дф + Эг = 0 ,	(9)
г дг г дф дг
1 ^ ЭЬ _ э ± = 0 г дф дг     ,	(10)
Эт^ - Эт" = 0 , дг дг	(11)
1 ф । д ! ф 1 д ) т о г    дг г дф     .	(12)

Решение этой системы уравнений имеет вид:

Hr = hr (r)sin(a

Нф = hф (r)cos( аф + xz),(14)

Hz = hz (r)sin( аф + xz),

Jr = Jr (r)cos( аф + XZ),(16)

/ф = Уф (r)sin( аф + xz),(17)

Jz = Jz (r)cos( аф + XZ),(18)

где a, X — некоторые константы, h(r), j(r) - некоторые функции координаты r. Эти функции определены следующими уравнениями: hZ (r) + hZ (r) - hz (r) (^ + x2) = 0, hv (r) = "(^ jr (r)),(20)

hr(r) = - X (hz (r) + Jф(r)),(21)

Jz(r) + J‘(r) r - Jz(r) (5 + X2) = 0,(22)

Jф(r') = —a-^,(23)

Jr (r) = -X-jzQr).(24)

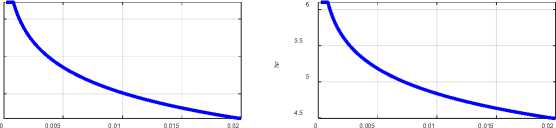
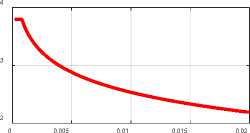
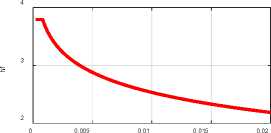
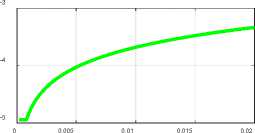
Fig. 3 (Meissner.m)

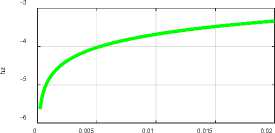
r

Важно отметить, что

имеют при данных a, X

и в этом случае восемь уравнений (5-12)

единственное решение в виде шести уравнений (19-24). На рис. 3 показаны графики логарифмов этих функций при а = 0.5, % = 0.1, R = 0.02.

Токи и магнитные напряженности распределены так всегда , даже в том случае, когда в проводе существуют только тепловые токи. Так происходит потому, что токи взаимодействуют между собой силами Лоренца и именно это взаимодействие описывается уравнениями Максвелла. Если к тепловым токам добавляется ток проводимости, то в математическом описании меняются только значения констант а, % . Точно тоже самое происходит в том случае, когда провод попадает во внешнее магнитное поле: меняются только значения констант а, % . Изменение магнитного поля меняет лишь значения констант. Важно, однако, чтобы напряженность магнитного поля была не равномерной. В [3, глава 5d] описываются различные эксперименты, демонстрирующие явление возникновения постоянного электрического тока под воздействием постоянного магнитного поля.

Таким образом, магнитное поле в проводе не вытесняется, а создается вновь и вместе с этим полем создаются токи. При малом внутреннем сопротивлении диска токи принимают большие значения.

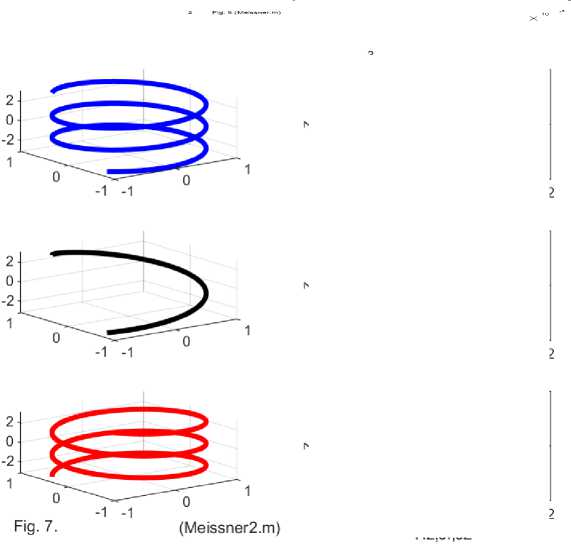
Ток в проводе имеет солиноидальную структуру. Поэтому можно рассматривать его, как соленоид. На рис. 4 показаны три винтовые линии тока: толстая линия при а = 2, % = 0.8 , средняя линия при а = 0.5, % = 2 и тонкая линия при а = 2, % = 1.6 . Показаны винтовые линии для функций / , определенных по (17, 18), а именно для суммарного тока с проекциями /^ и J_z при г = const . Эти функции определены при а > 0.

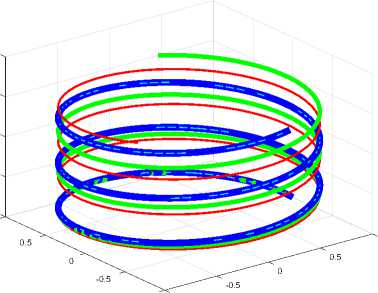
Рис. 4.

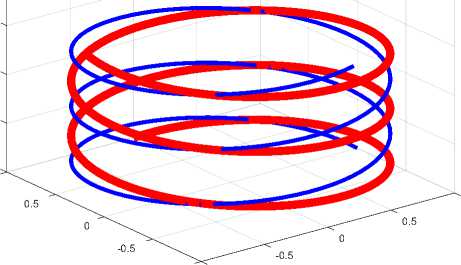
Рис. 5

На рис. 4 показаны винтовые линии

• •    для функций / , определенных при а > 0 как на рис. 3 (см. тонкую линию) и

• •    для функций / , определенных при а < 0 (см. толстую линию).

При а > 0 окружные токи исчезают - см. J^ (г) в формуле (23). Однако уравнение (4), по-прежнему, соблюдается. При а > 0 изменяется также знак функции H_z — см. (15).

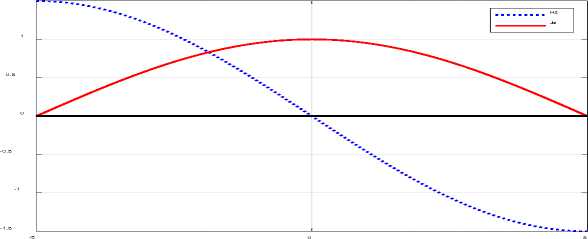
Все уравнения выполняются также для провода ограниченной длины – в нашем случае, для диска. На рис. 5 показаны функции (1318) на проводе, длина которого равна L = 2^у . Видно, что осевой ток ]_z (сплошная линия) принимает нулевое значение на концах провода, а осевые магнитные напряженности H_z и круговой ток /^ (пунктирная линия) на концах провода принимают максимальные и противоположные по знаку значения.

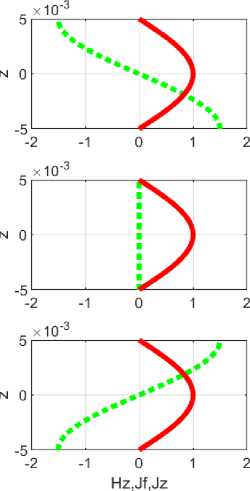
На рис. 7 показаны различные функции для трех положений диска в предположении, что магнит находится сверху, при этом в средних окнах показаны функции для устойчивого положения. Показаны функции только для одного значения радиуса. В правых окнах показана спираль линии тока, а в правых окнах показаны зависящие от Z функция /z (сплошная линия) и функции Hz , /^ (пунктирная линия). 1.5