Теоретическое обоснование параметров дозатора с цилиндрическим рабочим органом

Введение. Большое количество конструкций дозаторов в сельском хозяйстве и перерабатывающей промышленности обусловлено разными требованиями, предъявляемыми к процессу дозирования. Главное требование к дозаторам – это обеспечение подачи в смесь установленного по рецепту или технологии количества компонентов. Несоблюдение этого требования может снизить качество технологического процесса и привести к перерасходу дорогих компонентов, которые дозируются [1–3].

Проблемой любого из описанных выше производств является правильный выбор типа дозатора, который был бы простой по конструкции, имел минимальную энергоемкость, а главное обеспечивал бы объемное дозирование компонентов смеси с заданной степенью точности при разной производительности [3, 4].

Таким образом, ученые предпринимают попытки усовершенствования технологического процесса дозирования сыпучих компонентов в направлении со- здания машин, которые используют новые принципы и факторы, существенно влияющие на процесс дозирования. При этом высокая точность и качество дозирования должны сопровождаться сокращением энергозатрат на процесс.

Целью данной работы является теоретическое обоснование основных параметров объемного дозатора непрерывного действия с цилиндрическим рабочим органом и выявление существенных факторов, которые влияют на его конструктивные и технологические параметры.

Материалы и методы исследования. Увеличение масштабов производства вызвало необходимость применения непрерывных способов выполнения технологических процессов и выдвинуло новые требования к дозаторам [3, 4, 5].

При обработке сыпучего материала (дозирование, смешивание) широко используются непрерывнодействующие машины, рабочим органом в которых является вращающийся барабан [6, 7].

На основании анализа литературных данных, теоретических и экспериментальных исследований ряда авторов нами в качестве объекта дальнейшего исследования выбран технологический процесс объемного дозирования с разработкой дозатора непрерывного действия с цилиндрическим рабочим органом [8].

Исследования базируются на методе «вязких течений», в котором в первом приближении движение материала принимается как течение вязкопластической среды и используется подход к решению гидродинамической задачи с подобными предельными условиями [3].

Результаты исследования и их обсуждение. Исходя из проведенного анализа литературных и патентных источников и результатов теоретических исследований был разработан объемный дозатор непрерывного действия с цилиндрическим рабочим органом без внутренних устройств, который отличается простотой конструктивного выполнения и надежностью в работе [9, 10].

Процессу дозирования наиболее полно отвечает случай, когда в поперечном разрезе рабочего органа поддерживается режим переката или начальный участок водопадного режима, а в продольном – участки загрузки, транспортировки и разгрузки.

Известно также, что формирование продольного сечения материала в цилиндре происходит с выгрузного конца [11], что определяет производительность рабочего органа.

Немаловажную роль при этом в формировании продольного сечения материала в цилиндре, повышении производительности и точности дозатора играет угол наклона цилиндрического рабочего органа α . По результатам исследований [11–15] оптимальный угол наклона цилиндрического рабочего органа (шнека) для транспортировки сыпучего материала должен составлять от 15 до 30° .

Скорость движения частиц в слое, который скатывается, определяет осевую скорость перемещения материала во вращающемся цилиндре. Получить точные аналитические уравнения, которые описывают движение материала в плоскости вращения цилиндра, чрезвычайно тяжело. Поэтому мы применяем некоторые допущения, которые сохраняют основное физическое содержание задачи, но математические операции значительно упрощаются.

Исследование поставленной задачи базируется на методе «вязких течений», в котором в первом приближении движение материала принимается как течение вязкопластической среды и используется подход к решению гидродинамической задачи с подобными предельными условиями. Исходными уравнениями при этом являются: уравнение движения (равновесия) и уравнение, которое описывает реологические свойства сыпучей массы.

При решении задачи принимается гипотеза о сплошной среде и делаются следующие допущения (Макаров Ю.И. Аппараты для смешения сыпучих материалов. М.: Машиностроение, 1973. 216 с.).

• 1.    Инерционные силы частиц, которые двигаются, незначительны через их малую скорость и не учитываются в сравнении с массовыми.

• 2.    Длина скатывающегося слоя по поверхности откоса больше по сравнению с его толщиной, поэтому не учитываются конечные эффекты в крайних точках 3 = 3 0 и 3 = о .

Сделанные допущения позволяют составить уравнение движения (равновесия) скатывающегося слоя в цилиндрических координатах вдоль оси 3 (рисунок 1).

1da 1 d ( 2 х      Л/п

+ ~т( rT)± pg = 0,(1)

r d3 r dr ''

где r – текущее значение радиуса рабочего цилиндра R ц ;

• a    - нормальное напряжение материала в слое;

• 3 - угол обхвата сегмента сыпучего материала в цилиндре;

т - касательное напряжение материала в слое;

р - насыпная плотность материала.

При — = о, -1»1 и если т есть d3     й функция только 3, то уравнение (1) можно записать в виде dT - рg • sin в = 0,        2)

dr где в - динамический угол естественного откоса;

h – толщина скатывающегося слоя.

Реологическое уравнение, которое связывает касательное напряжение со скоростью скатывания частиц сыпучего материала по поверхности откоса, имеет следующий вид:

т = т о ⁺ п d ⁹ .      (3)

dr

Решая совместно уравнение (2) и (3), получим аналитическое выражение для определения скорости движения материала по поверхности откоса.

^„ = eg™ в п

(Rc-r)

- R ( R c - r )

- п ( “ - r ) ^,

где т₀ - предельное напряжение сдвига;

п - коэффициент «внутреннего трения» материала;

R c – радиус слоя скатывания.

Количество материала в скатывающемся слое Q , проходящего через сечение МN (рисунок 1) в единицу времени, определяется из выражения

R ц

Q .K = L f 9. ■ dr,         (5)

Rc где L – длина цилиндра.

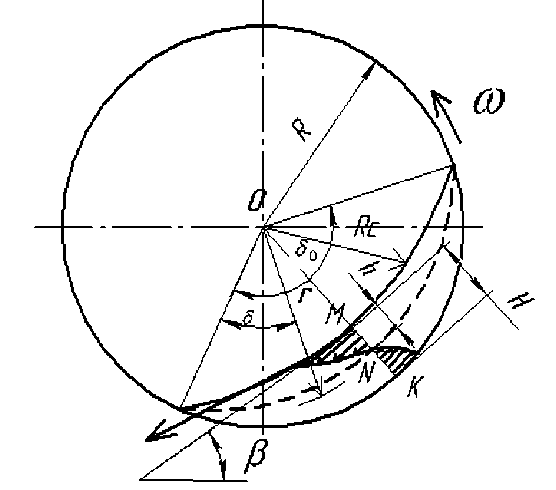
Рисунок 1 – Схема движения материала в плоскости вращения цилиндра

Figure 1 – Diagram of the movement of the material in the plane of rotation of the cylinder

Подставляя &_ск из уравнения (4) в (5) и интегрируя в пределах R_ц - R c , получим:

Q ck = L —Si" в n

(R-RJ

_T (R - R У ^то     c     ц)

П    2

Так как r_c - r* = h , то

Q_CK = L ^ gh ' sin в - ^h ² ск

3 ц          2 ц

.

Толщина скатывающегося слоя «h » находится из условия неразрывности потока, то есть количество материала, который скатывается, по поверхности откоса равняется количеству материала, который поднимается вместе с поверхностью цилиндра.

Q ck = Q n .

Количество материала,

(8) который

поднимается, находится из выражения

Qn = — (H - h) L .

r

Сравнивая уравнения (7) и (9) и вводя обозначение — = м , — = n и 3ц

— = с , получим выражение для 2

тол-

щины скатывающегося слоя:

Mh3 - Nh3 = C(H - h) .

Толщину скатывающегося слоя можно определить графическим методом. Для этого строится график зависимостей (рисунок 2) Mh ³ - Nh ³ = f(h) и

C(H - h) = f₂(h) .

Точка пересечения кривых будет характеризовать значение толщины слоя сыпучего материала, который скатывается во вращающемся цилиндре. Так, при диаметре рабочего цилиндра D = 0,08 м, частоте его вращения n = 70 об/мин и угле наклона a = 20° толщина скатывающегося слоя для сыпучего материала комбикорма при К = 0,2 будет равняться 0,021–0,022 м.

При движении сыпучей массы в рабочем органе поперечное её сечение имеет сложный вид, математически описать который сложно. Кроме того, вид предельной линии зависит от коэффициента кинематического режима цилиндра (отношение центробежной силы к весу частиц), угла наклона и свойств поверхности материала.

На исходном участке вследствие конечного эффекта материал располагается под динамическим углом естественного откоса к горизонту, создает поверхность опадания (осыпь) (рисунок 1). В общем случае эта поверхность имеет сложный вид, который зависит от кинематических и геометрических параметров аппарата и свойств поверхности материала.

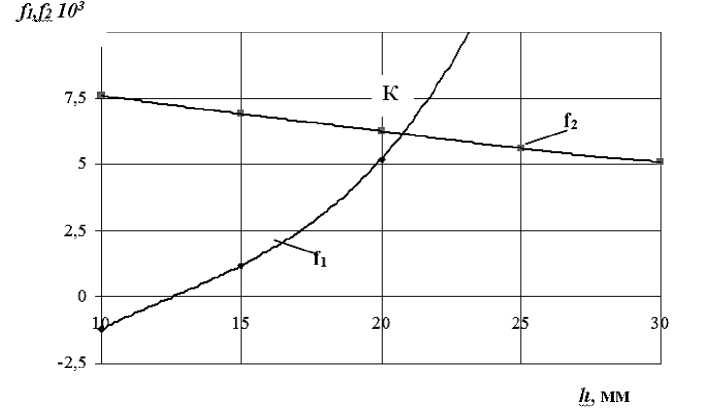
Рисунок 2 – Графический способ определения толщины скатывающегося слоя сыпучего материала Figure 2 – A graphical method for determining the thickness of a rolling layer of bulk material

При принятых допущениях искривлением осыпи можно пренебречь и аппроксимировать её плоскостью, которая проходит под углом динамического отко- са р к горизонту.

Длительность цикла для точек, ко- торые проходят самый большой путь, max    max   max ц       tn       toc

.

Здесь t max,t max – длительность со- ответственно цикла подъема и осыпания материала.

Очевидно, m = — . п     а

Длительность цикла осыпания при равноускоренном движении материала по осыпи max toc где l – максимальный путь скатывания;

g – ускорение скатывания.

Путь скатывания (рисунок 2)

r [ 1 - sin ( — 1 + — 2 ) ]

l =        3          , sin у

где угол γ – разница между углом динамического откоса р и углом наклона а .

На частицу, которая двигается по поверхности осыпи, действуют силы веса частицы и трения о поверхность. Проектируя их на направление движения частицы, получаем:

mg c = ^F c ^{— F} m ;

mg_c = mg sin ф — mg cos ф • f_m;

• g c = gc^os^ ( ^tg ^{ф —} f т ) , где f – коэффициент внутреннего тре-

• ния материала;

  – силы соответственно скаты-

• c, m

вания и трения.

В этом случае

Здесь к =

n ²n²D

1800 g

– коэффициент

max t_oc

2r 1 - sin ( S + S )

g^sin Y • cos ^ ( tg ^ ^- f m ) '

кинематического режима;

a = i ;

Ф

Максимальная длительность цикла

max   ^S

ц

a

2r 1 - sin (Sj + S ) ^ gsin y • cOs^^^tg ^{ф -} f m )

С учетом того, что длительность

1 - sin ( S + S )

В =                           V.

Ф ^ sin ( ф - a ) cos ф ( tg ф - f m )

Массовая производительность

Q m = 7  ^    ,  (16)

цикла определена для частиц, которые проходят самый большой путь, в формулу производительности необходимо ввести среднее время цикла, который равняется приблизительно половине макси- мального.

Поэтому имеем

Q =------ 'r"     .

tg ( ф - a ) ( А + В4К )

где p - насыпная плотность материала.

После преобразований имеем

Q =   <  ³^Dn Г-x ,   (17)

tg ( в - a )( A + bJk )

где D – диаметр цилиндра;

n – частота вращения цилиндра.

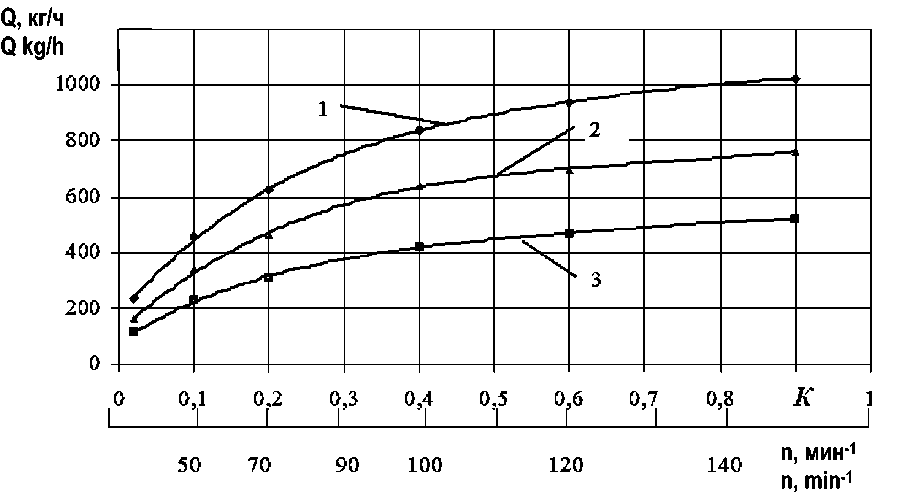
Рисунок 3 – Зависимость часовой производительности дозатора Q от коэффициента кинематического режима K ( D = 0, 08 мм) и частоты вращения рабочего цилиндра n при a : 1 - 20; 2 - 15; 3 - 10°

Figure 3 – Dependence of the hourly productivity of the dispenser Q on the kinematic mode coefficient K ( D = 0,08 mm) and the rotation speed of the working cylinder n at a : 1 - 20; 2 - 15; 3 - 10°

На рисунке 3 показана зависимость часовой производительности дозатора Q от коэффициента кинематического режима K ( D = 0, 08 мм) при α : 1 – 20; 2 – 15; 3 – 10°, вычисленная по формуле (17).

Анализ рисунка 3 показывает, что с ростом коэффициента кинематического режима больше 0,5 производительность дозатора возрастает медленно, поэтому выбираем следующий режим работы дозатора (особенно для микродозирования при производительности до 400 кг/ч): коэффициент кинематического режима 0 <  К < 0,4; частота вращения рабочего цилиндра до 100 об/мин.; диаметр цилиндра до 0,08 м.

Выводы . Проведенные теоретические исследования позволяют сделать следующие выводы.

• 1.    Скорость движения частиц в скатывающемся слое определяет осевую скорость перемещения материала во вращающемся цилиндре. Получены аналитические уравнения, которые описывают движение материала в плоскости вращения цилиндра: это скорость движения частиц сыпучего материала в скатывающемся слое (формула 4) и толщина скатывающегося слоя сыпучего материала (формула 10).

• 2.    Основными факторами, которые влияют на производительность дозатора непрерывного действия с цилиндрическим рабочим органом, являются: физико-механические свойства дозируемого материала (насыпная плотность материала ρ , коэффициент трения f ), а также конструктивные параметры дозатора (длина цилиндра L, его диаметр D и угол наклона α ) и режимы работы (частота вращения цилиндра n и коэффициент кинематического режима К ).

• 3.    Теоретически обоснован режим работы дозатора (особенно для микро-

• дозирования при производительности до 400 кг/ч):

  – коэффициент кинематического режима 0 <К<0,4;

  – частота вращения рабочего цилиндра до 100 об/мин.;

  – диаметр цилиндра до 0,08 м;

  – угол наклона рабочего цилиндра α =10–20°;

  – толщина скатывающегося слоя при К = 0,2 должна равняться h = 0,021– 0,022 м.