Теоретическое обоснование снижения раскачивания груза на канате строительного крана

Известно, что раскачивание груза на канате строительного крана – опасный и неустранимый процесс, следствием которого является длительное уравновешивание груза, что увеличивает напряженность труда крановщика, усложняет работу стропальщиков на строительной площадке, снижая при этом темп работ и производительность труда в целом. Мероприятия по уменьшению колебаний груза на грузовом подвесе строительного крана могут привести к существенному повышению производительности строительно-монтажных труда (≈ на 20%) [1].

Инженерно-техническое решение, разработанное на уровне изобретения [2], основано на предположении сокращения периода колебаний гибкого подвеса с использованием присоединения дополнительной массы.

Основанием для такого предположения послужила известная теорема об изменении периода маятника от присоединенной массы, приведенная в монографии «Определение моментов инерции» М.М. Гернета и В.Ф. Ратобыльского [3]: «от присоединения к физическому маятнику точечной массы период его качаний уменьшится, если масса присоединена к маятнику между осью подвеса и центром качания, и увеличится, если масса присоединена ниже центра качания».

При доказательстве теоремы авторы рассматривают тело, подвешенное в точке О , которое может качаться относительно горизонтальной оси, проходящей через точку подвеса О (рис. 1), с периодом:

Т1 27ГJ2К l , (1) mgc \/ g где: m – масса маятника; J= mcl – момент инерции относительно оси подвеса; l – приведенная длина. Известно, что длина математического маятника, качающегося синхронно с физическим маятником, называется приведенной длиной физического маятника [3].

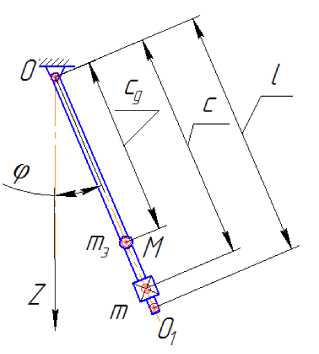
Рисунок 1 – Схема маятника сравнения и иллюстрация к теореме о присоединенной массе

_Т= mi Ui m 2W2

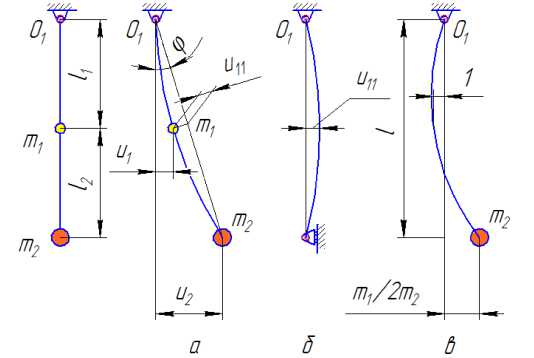
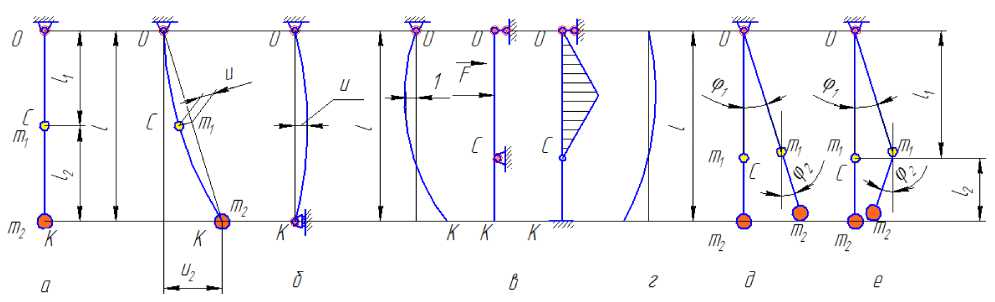
Рисунок 2 – Расчетная модель к задаче о сокращении периода колебаний при закреплении груза в середине подвеса

Если к маятнику, находящемуся в равновесии, в точке М, лежащей ниже оси подвеса на одной с ней вертикали на расстоянии ОМ=сЭ, присоединить неко- торую точечную массу mЭ , то период малых колебаний маятника с присоединенной массой будет равен:

mcl mэсэ2

²  ^ g ( mc + m₃ С э )

c2

mc m э

2                      ^l . (2)

g mc mэcэ

Таким образом, Т 2 < Т 1 , если второй радикал в выражении (2) меньше 1, а

При определении потенциальной энергии изгиба подвеса его можно рассматривать как балку на двух опорах (рис.2, б, в). Поскольку изгибающие моменты в верхней и нижней точках равны 0, то потенциальная энергия будет равной сu 11

П       , где

6EIX  жесткость кон- c3

l 1 ( 2 )

сольной балки при изгибе. В случае малых       колебаний        u_x=1_x sin

«I; cp;

u2 =(1V+12)sin

mc m

cэ²

допущения уравнения движения масс

l

mc m c

или c l ,  (3)

примут вид:

в противном случае период колебаний

увеличится.

Данная теорема подтверждается решением известной задачи, приведенной в сборнике задач по теории колебаний В.А. Светлицкого и И.В. Стасенко [4].

Условие задачи. На гибком подвесе длиной l (l=l1+l2, l1=l2) закреплены две точечные массы m1 и m2 (рис. 2, а, б, в). Жесткость подвеса EIx. Пренебрегая действием силы тяжести и массой подвеса определить частоту и формы собственных колебаний системы в плоскости чертежа.

Кинетическая энергия системы в произвольный момент времени (рис. 2, а) будет равна:

c mxUx c-uux~uU2 =0;

cc mu u u 0 224221

Характеристическое уравнение для этой

системы примет вид:

p²

2  cm m m p     1 cm

где р – частота колебаний системы, 1/с. Из уравнения (6) получено значения час-

тоты с учетом подстановки значения же-

сткости системы при изгибе:

Pi = °, p2 =

J 6 EI_X(m_x +4 m₂)

4l³m m

При условии, что   Е=2∙10¹¹Па;

Ix=0,05∙d⁴=0,05⁵(м⁴); m1=20 кг; m2=500 кг;

l=40 м, ; l1= l2=20 м, получаем: р2=0,694 1/c, а Т=2π/p2 =9,06 (с), что в 1.39 раза

меньше, чем период колебаний маятника с l=40 м и ; m2=500 кг без присоединенной массы.

Т.о., следует полагать, что при закреплении посередине гибкого подвеса длины l дополнительной массы m1, значительно меньшей массы основного груза, период колебаний системы сокращается примерно в 1.4 раза, что может являться основанием для дальнейших рассуждений, а именно: должна существовать зависимость между периодом колебаний гибкого подвеса от его длины, масс основного и присоединенного грузов и места расположения последнего по длине подвеса, которая позволит разработать способ и устройство, направленные на стабилизацию колебательного процесса грузового каната строительного крана.

Для получения такой гипотетической зависимости необходимо определиться с моделью, на основании которой возможен вывод уравнения.

Большинство исследователей данной проблемы в качестве модели выбирают математический маятник, то есть для исследования колебательной системы «канат – груз» можно принять следующие условия:

• -    грузовой канат представляет собой гибкий подвес, масса которого мала по сравнению с массой поднимаемого груза, и, следовательно, может не учитываться;

• -    относительное удлинение (растяжение) каната под действием силы тяжести поднимаемого груза или каких-либо внешних динамических нагрузок невелико по сравнению с длиной каната, и поэтому может также не учитываться;

• -    размеры поднимаемого груза и присоединенной массы малы по сравнению с длиной каната, следовательно, массы m1 , m2 , могут считаться точечными, то есть моменты инерции грузов не учитываются.

Т.о., гибкий подвес «канат-груз» может быть смоделирован в виде математического маятника, совершающего малые свободные колебания. При этом будем считать систему консервативной, а колебания незатухающими.

Однако прежде чем перейти к выводу гипотетической зависимости, выясним с помощью основных сведений из теории ошибок:

• 1.    Какова погрешность от пренебрежения размером груза;

• 2.    Какова погрешность допущения, что грузовой канат невесом и нерастяжим.

Известно, что физический маятник – это тяжелое твердое тело, имеющее возможность свободно вращаться на оси под действием силы тяжести [3] (рис. 3, а). С теорией физического маятника тесно связана теория математического маятника, состоящего из одной материальной точки массой m, совершающей под действием своего веса плоские колебания около неподвижной точки О, с которой она соединена невесомой и нерастяжимой гибкой нитью длиной l (рис.3, б). При этом периоды малых колебаний физического и математического маятников определяются согласно известным выражениям [3]:

Тф 2л J ^J ; T_M  2Л^ ^l ,     (8)

\1 mgc            g где: J – момент инерции тела относительно оси вращения, кг∙м2; m – масса тела, кг; с – расстояние от оси подвеса до центра масс, м; l – длина нити, м.

Период колебаний математическо- го маятника сравнения, качающегося синхронно с физическим маятником оп- ределяется выражением [3]:

т ср

2л

J+ml² mgl

...   2л

J

1+ ^c ml

Т,

где Jc – момент инерции груза относительно центральной оси, параллельной оси подвеса, кг∙м2. Согласно теореме Гюйгенса-Штейнера-Эйлера [5] момент инерции груза относительно оси подвеса равен:

J J_c +ml.

Момент инерции груза Jc относительно центральной оси, параллельной оси подвеса, увеличивает период колебаний маятника, но незначительно, поэтому можно принять Тф ≈Тср ≈Тм. . Убедимся в этом на конкретных примерах.

Рисунок 3 – Схемы колебательной системы типа «маятник»: физический, математический сравнения

где в качестве точной оценки будем рассматривать период колебаний маятника с учетом размера груза, веса и длины нити, а в качестве приближенной оценки – период колебаний математического маятника.

Рассмотрим, какова погрешность от пренебрежения размером груза. В качестве груза примем балку сборную железобетонную обвязочную БП3-1 с размерами 5500х250х290 мм и железобетон- ную плиту перекрытия размерами 12000х1500х220 мм. Длину подвеса примем переменной: 10, 20, 30 м. Момент инерции балки относительно центральной оси (рис.3, в) определяется по фор-

Точность приближенной формулы оценивают относительной погрешностью, определяемой выражением [3]:

муле:

Jc

b²h²

m, 12

FF

F         точн прибл прибл                     , точн

где b, h –линейные размеры балки. Результаты вычислений приведены в табл. 1.

Таблица 1 – Результаты расчета погрешности от пренебрежения размером груза

Длина подвеса l, м	b, м	h, м	Тм, с	Тср, с	Погрешность δразм
Балка обвязочная БП3-1
10	5,5	0,29	6,341	6,417	0,012 или 1,20 %
20			8,967	8,967	0,003 или 0,30%
30			10,982	10,993	0,001 или 0,10%
Плита перекрытия железобетонная
10	12	0,22	6,341	6,709	0,055 или 5,5%
20			8,967	9,102	0,015 или 1,5%
30			10,982	11,048	0,006 или 0,6%

Приведенные в табл. 1 данные расчета погрешности периода колебаний грузового подвеса при условии пренебрежения размерами груза позволяют сказать, что значения погрешности незначительны, когда размер груза меньше длины подвеса, и допустимы в случае, когда размер груза соизмерим с длиной подвеса. Погрешность уменьшается, а значит, точность возрастает с увеличением расстояния от центра тяжести груза до оси подвеса.

Рассмотрим далее, как влияет на период колебаний грузового подвеса его вес и длина.

При условии, что Jc – момент инерции груза относительно центральной оси симметрии, кгм2; m – масса груза, кг; l – длина нити, м; μ – масса нити, кг, период колебаний маятника сравнения с учетом массы нити определяется выражением (13) [3]:

^Tср   ²

J     l ml c3

g ( ml+¹Hl)

Исходные данные и результаты расчетов приведены в табл. 2.

Таблица 2 – Результаты расчета погрешности от пренебрежения массой и длиной нити

Длина подвеса l, м	m, кг	b, м	h, м	Ц , кг	Тм, с	μ ср, с	Погрешность δm,l
Балка обвязочная БП3-1
10	500	5,5	0,29	23,4	6,341	6,393	0,008 или 0,80 %
20				46,8	8,967	8,924	-0,005 или -0,50%
30				101,4	10,982	10,827	-0,014 или -1,40%
10	500	5,5	0,29	46,8	6,341	6,368	-0,004 или -0,40 %
20				93,6	8,967	8,867	-0,011 или -1,10%
30				202,8	10,982	10,682	-0,028 или -2,80%

Период колебаний груза на весомой нити уменьшается с увеличением массы и длины нити. Причем период колебаний маятника на весомой нити меньше, чем математического маятника такой же длины, вероятно потому, что вес нити приложен между грузом и точкой подвеса (результат согласуется с теоремой о присоединенной массе). При этом влияние массы и длины нити на абсолютное значение периода колебаний незначительно.

Известно, что под действием динамической нагрузки даже хлопчатобумажная нить практически не изменяет своей длины [3]. Натяжение нити меняется в зависимости от угла наклона маятника в следующих пределах [3]:

Rmin mgcos V0; Rmax mg(1 +ф0^2),

где φ0 – угловая амплитуда колебаний маятника. При больших амплитудах изменение натяжения невелико.

Таким образом, в целом результаты вычислений показывают, что размеры груза, масса и длина подвеса на период колебаний влияют незначительно, а поэтому нить можно принимать идеальной, а маятник сравнения – математическим.

Таблица 3 – Влияние на натяжение нити значения угловых амплитуд маятника

ф0 , град.	5	10	15	20	25
Rmax , Н	1,00mg	1,03 mg	1,07 mg	1,12 mg	1,19 mg
Rmin, Н	1,00 mg	0,98 mg	0,97 mg	0,94 mg	0,91 mg

Т.о., в целом результаты вычислений показывают, что размеры груза, масса и длина подвеса на период колебаний влияют незначительно, а поэтому нить можно принимать идеальной, а маятник сравнения – математическим.

На основании анализа известных методов исследования динамических систем типа «маятник» и прикладных задач теории колебаний, представленных в работах М.А. Красносельского, В.И. Зубова, Л.И. Мандельштама, А.Ю. Ишлин-ского, К. Магнуса, Т.Г. Стрижак, А.П. Маркеева, М.М. Гернета, В.Ф. Ратобыль-ского, С.П. Стрелкова, В.А. Светлицкого, И.В. Стасенко, М.И. Батя, Г.Ю. Джани-лидзе, А.С. Кельзона, Я.Г. Пановко и других [3-8], было проведено теоретическое исследование существования воз- можности снижения периода колебаний за счет изменения системы подвеса с использованием «присоединенного» груза [9,10].

Реальная колебательная система «канат – груз» была рассмотрена с учетом следующих допущений: поднимаемый груз, размеры которого значительно меньше длины грузового каната, представляет точечную массу m2; последняя закреплена на нерастяжимом канате длиной l, масса которого значительно меньше массы поднимаемого груза, а поэтому ее влияние на колебательный процесс не рассматривалось; канат шарнирно закреплен в точке О (Рисунок 4,а); канат принят нерастяжимым стержнем. На расстоянии l1 от точки О на стержне установлен дополнительный груз в виде то- чечной массы m1 (точка С). Общая длина стержня l определяется выражением: l= l 1+ l 2 , при этом l 1 ≠ l 2, l 2 – расстояние от точки С до центра масс основного груза m2 (точка К). Система «канат – груз» вращается относительно горизонтальной оси OX, расположенной перпендикулярно плоскости чертежа и проходящей через точку О. При этом стержень можно рассматривать аналогично расчетной схеме рассмотренной выше задачи [4] как вертикальную балку на двух опорах (рис. 4, б) с различными формами колебаний. Грузовой подвес может быть рассмотрен и как вертикальная балка на двух опорах с консолью (рис. 4, в) и сосредоточенной активной силой F в пролёте ОС, вызванной эксплуатационно-техническими причинами или ветровыми воздействиями (равномерно распределенная ветровая нагрузка может быть заменена сосредоточенной силой). Этой балке соответствует фиктивная балка с распределенной определенным образом нагрузкой в пролете и соответствующими схеме загру-жения изгибами (рис. 4, г). Кроме того, стержень можно рассматривать и как балку с шарнирно сочлененными составляющими ОС и СК, что, по сути, представляет собой при принятых выше допущениях двойной математический маятник, способный принимать различные колебательные формы (рис. 4, д, е).

Приведем исследование малых колебаний двойного маятника с двумя степенями свободы φ1,φ2 посредством использования известных выражений для вычисления главных колебаний, завися- щих от параметров маятника [3], при этом первое главное колебание (рис. 4, д) происходит так, что нити ОС и СК в каждое мгновение могут быть отклонены по одну и ту же сторону от вертикали. Отношение углов, образованных ОС и СК с вертикалью, остается постоянным φ1 :

φ2=β1. Во втором главном колебании (рис. 4, е) углы отклонения находятся по разные стороны от вертикали при неизменном соотношении углов φ1: φ2=β2.

Частоты главных колебаний определяются следующими выражениями: ® 1     g-< 12 +Г? +1112-4 (l2 +r„² +1112 )²-4lil2 rU 1 ;

• l₁2r_и

  ®2 = ^< 12 ^+Г" ^^^(1'+ ru² +1112 )²-41112rU 1 , l₁2r_и²

где rи - радиус инерции груза m2 относительно центральной оси, то есть оси, проходящей через центр масс груза, м. Масса нитей мала по сравнению с массой основного груза и при выводе выражений (15) не учитывалась. Периоды главных колебаний маятника вычисляются согласно выражениям:

Т1=^;   Т2=^          (16)

В табл. 4 представлены исходные данные и результаты расчета периодов колебаний двойного маятника в зависимости от общей длины подвеса, расположения присоединенной массы на подвесе, радиуса инерции основного груза относительно центральной оси и формы главных колебаний.

Таблица 4 - Результаты исследования периода колебаний двойного маятника

l, м	l 1, м	l 2, м	ru, м	ω1,1/c	T1,c	ω2,1/c	T2,c	Tсред,c	Т,c без m1
20	15	5	2,75	0,339	18,525	3,031	2,072	10,299	8,967
20	18	2	2,75	0,693	9,062	1,717	3,657	6,360	8,967
20	17	3	1	0,700	8,971	5,892	1,066	4,822	8,967
30	25	5	1	0,571	10,998	7,676	0,818	5,908	10,982

Анализ приведенных в табл. 4 результатов исследования периода колебаний двойного маятника позволяет предположить, что присоединенная масса m1, вес которой незначителен, и поэтому не учитывался, может способствовать снижению периода колебания гибкого подвеса, причем уменьшение периода колебаний зависит от места расположения присоединенной массы по длине подвеса.

Чем меньше расстояние от центра масс основного груза до места расположения дополнительного груза, тем существеннее влияние последнего на снижение периода колебаний двойного маятника. Грубое предположение того, что первое и второе главные колебания равно возможны, позволило рассчитать среднее значение периода колебаний Тсред, которое, в случае низшего положения m1 на подвесе, значительно меньше периода колебаний математического маятника с одной точечной массой m2.

Перейдем к выводу зависимости, позволяющей в производственных условиях реализовать способ, направленный на уменьшение колебаний грузового подвеса.

Воспользуемся известным дифференциальным уравнением для вращения твердого тела вокруг неподвижной оси [11]:

Ix (( = m (F ),        (17)

i1

где: IX – момент инерции твердого тела относительно оси вращения OX; (р - угловое ускорение подвеса; m F^e – момент внешних сил, приложенных к подвесу, относительно оси ОХ.

Если рассматривать грузовой подвес как сплошной невесомый стержень с присоединенной на нем точечной массой m1 на расстоянии l1 от оси закрепления подвеса и точечной массой m2 , имитирующей основной груз, установленный на конце подвеса на расстоянии l от его оси (рис. 4, а), то момент инерции должен определяться выражением:

I    ml²  m l²,                 (18)

а сумма моментов всех внешних сил относительно оси вращения равна n.m_x(F^e)=mggl_x sinq>-m₂gl sinq>, (19) _i1X i            1    1                2

где φ – угол отклонения грузового подвеса от вертикали.

Однако следует отметить, что помимо колебания подвеса относительно оси, проходящей через точку его закрепления (точка О), возможно и самостоятельное колебание части подвеса l2 с грузом m2 относительно оси (СХ1), перпен- дикулярной плоскости чертежа и проходящей через точку С закрепления дополнительного груза m1 (рис. 4, б).

Исследования колебаний динами- ческих систем типа «маятник» с целью определения эффективных путей, направленных на разработку механических гасителей колебаний, свидетельствуют, что при определенных возмущениях воз- можны ситуации, при которых первая масса (m1) может оставаться в покое [12]. Кроме того, воспользуемся для дальнейших рассуждений понятием парциальной системы, то есть системы с одной степенью свободы, которая получается из данной системы с двумя степенями свободы при «закреплении» одной из координат [12].

При таком условии колебания масс m1 и m2 совершаются самостоятельно, соответственно, относительно осей

ОX и CX1 , тогда исходя из требования

(17) уравнения (18) и (19) примут вид:

Ix —m₁^l₁;

Ix1 ^=m2¹2 ^;

_< mx⁽Ft⁾⁼-m1 g^l1^sinФр   ₍₂₁₎

^mX! ^(Fi⁾⁼-m2g^l2 ^sin(P2 ;

При    допущении    условия

, что возможно только при малых колебаниях системы, а именно они и имеют место в реальной производственной обстановке, и подстановке (20), (21) в (17) получаем:

(m_xl2 +m₂l₂2)((=-(mj_x mn₂l₂)gsin

.

Отсюда находится угловое ускорение системы: ml ml

((=--L2   2-2^g smq) , или ml ml ml ml

⁽   72   ^,2 gSiⁿ⁽P=0   ⁽²²⁾

m₁l₁   m₂l₂

Известно, что дифференциальное уравнение колебаний математического маятника имеет вид [11]:

g

(р+уsmq>=0 .

Если принять в качестве длины эквивалентного математического маятника выражение [13]:

m₁l₁    m₂l₂

ml ml

то при условии малых колебаниях маятника, когда sin ср^ф , уравнение (22)

примет вид аналогичный уравнению (23).

Уравнение (22) можно предста-

вить в виде ф+о2ф=0 ,

где

ml ml

2       1₂1     2 2_{2g .}

m₁l₁   m₂l₂

Гипотетический период свободных колебаний, описываемых уравнением (26), будет равен

2я

_T2   ₂

со

m₁l₁  m₂l₂

V (mill +m2l2 )g

.

Рассмотрим частные примеры изменения периода колебаний груза m2 на канате при изменении переменных l1 , l2, m1 , m2 . Результаты расчетов занесем в табл. 5.

Анализ полученных результатов позволяет предположить, что путем разбиения каната на две части, можно значительно сократить период и амплитуду колебаний груза, что позволит увеличить производительность монтажных и погрузочно-разгрузочных работ. При этом стоит заметить, что результаты расчета периода с использованием зависимости (27) подтверждают выше представленные: значение массы m1 дополнительного груза на период колебаний существенно не влияет, большее значение имеет место расположения дополнительного груза по длине каната (см. табл. 5).

присоединенной массы

Рисунок 5 – Схемы возможных колебаний вертикального подвеса с использованием

Таблица 5 - Результаты расчетов периода колебаний груза на канате

Сокращение периода колебаний, %	Т,с по (5.5)	Т,с по (5.54)	l, м	l 1, м	l 2 , м	m1, кг	m2, кг
29,3	12,68	8,97	40	20	20	100	1000
29,3	12,68	8,97	40	20	20	200	1000
14,0	12,68	10,86	40	10	30	100	1000
40,0	12,68	7,67	40	30	10	100	1000
84,0	13,45	2,17	45	30	15	100	1000
19,0	13,45	10,85	45	15	30	100	1000
30,0	13,45	9,51	45	22,5	22,5	100	1000
12	8,97	7,95	20	4	16	100	1000
39	8,97	5,46	20	16	4	100	1000
10	10,99	9,94	30	5	25	100	1000
38	10,99	6,85	30	25	5	100	1000

Решение известной задачи исследования функции путем определения ее экстремумов через частные производные, а также определение оптимальных значе- ний переменных для получения минимальных значений функции, то есть периода колебаний Т, определяемого выражением (27), представляет трудоемкую и сложную задачу. Поэтому для определения значений периода колебаний системы в зависимости от изменения начальных условий, то есть массы монтируемого груза, массы дополнительного (балластного) груза и его местоположения по длине подвеса, была написана программа для ПЭВМ, позволяющая найти оптимальные значения параметров m1 , m2 , l1 , l2 , что в свою очередь позволит в реальных производственных условиях добиться сокращения периода и амплитуды колебаний груза, увеличения производительности монтажных и погрузочноразгрузочных работ.

Полученные значения свидетельствуют, что при закреплении балластного груза в нижней части подвеса значительно снижается период колебаний системы «канат-груз» (в 2 – 3 раза), и согласуются со значениями, приведенными в табл. 5, рассчитанными по случайным значениям переменных.

Результаты теоретических и экспериментальных исследования легли в основу заявленного на уровне изобретения устройства [2], позволяющего реализовать данный способ по уменьшению периода колебаний грузового подвеса.