Теоретическое описание движения частиц зернового материала в прямолинейном канале треугольного сечения

Известно [1,2], что частицы зернового материала различной влажности отскакивают от поверхности при падении на разные расстояния. При обосновании основных параметров сепаратора для разделения частиц зернового материала по влажности необходимо исследовать движение частиц зернового материала по различным поверхностям. Для этого был разработан экспериментальный стенд-сепаратор разделения сыпучих материалов [3] (рис. 1,2).

Внутри загрузочного бункера, в нижней части, расположен барабан с продольными пазами, под ним скребок, прикрепленный к задней стенке бункера. Ширина паза соответствует ширине зерна. Такая конструкция позволяет предварительно ориентировать зерновые частицы продольной осью вдоль паза на барабане по ширине зерна. При вращении барабана за счет прилегающего скребка зерновые частицы подаются на прямолинейную скатную пластину не соприкасающимися порциями в один слой.

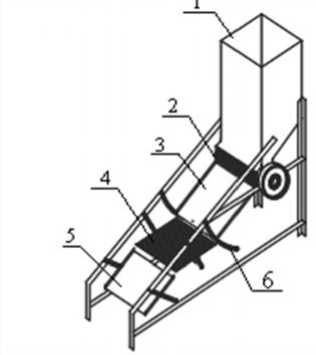
Рис.1. Сепаратор для разделения сыпучих материалов: 1 – загрузочный бункер; 2 – барабан с продольными пазами;

3 – скатная пластина; 4 – рифленая пластина; 5 – отражательная поверхность;

• 6 – направляющие пластин

Зерно представляет собой резко выраженное анизотропное тело: отдельные части зерна (оболочка, эндосперм, зародыш), имея различную структуру, различные физические и химические характеристики, обладают разными механическими свойствами, геометрический центр не совпадает с центром масс. Поэтому при движении частиц по прямой скатной поверхности происходит их переориентация: продольная ось зерновой частицы под действием трения и гравитационных сил становится расположенной вдоль направляющей скатной пластины. Ориентированные частицы после схода с гладкой скатной поверхно- сти попадают на гофрированную направляющую пластину. Шаг рифления выполнен по ширине зерна.

Это позволяет стабилизировать все кинематические характеристики движения зерновых частиц. Так уменьшается их отклонение от траектории движения, убирается вращение, из плоско-параллельного движение переходит в поступательное; скорость стабилизируется. Стабилизированные частицы после схода с гофрированной направляющей ударяются об отражательную пластину. В зависимости от влажности зерна происходит деление на фракции. Зерно с разной влажностью попадает в разные приемники продуктов разделения.

Данная установка изображена на рисунках 1,2.

Рис.2. Общий вид сепаратора для разделения сыпучих материалов

Для обоснования основных параметров установки необходимо определить: какой должна быть длина деки после барабана; как можно управлять зерновыми частицами за счет изменения угла наклона пластин и отражательной поверхности; как за счет изменения угловой скорости барабана можно регулировать начальную скорость движения зерновых частиц. То есть необходимо разработать математические основы инженерного расчета конструирования направляющих устройств.

Для теоретического описания процесса движения частиц зернового материала разделим движение на четыре этапа:

• - начальное движение зерновой частицы, заданное с помощью барабана с продольными пазами, позволяющего обеспечить отбор и предварительную ориентацию зерновых

частиц;

• -    переориентацию движения зерновой частицы под действием трения и гравитационных сил на скатной пластине;

• -    стабилизацию движения на рифленой направляющей;

• -    отскок от отражательной пластины.

Аналитически описано движение частиц зернового материала по различным поверхностям [4, 5].

Рассмотрим движение частиц зернового материала на рифленой направляющей.

Математическая модель стабилизированного движения на рифленой направляющей сводится к динамике точки, так как при стабилизации движения зерновой частицы отсутствуют вращательные составляющие.

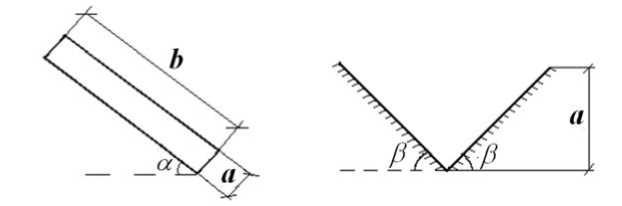
Рис. 3. Характеристики разгонного канала: a - угол наклона канала; b = 30 см -длина канала; а = 3 мм - глубина канала; в = 45° - угол наклона стенки канала

Рассмотрим более подробно динамику движения зерновой частицы в прямолинейном канале рифленой направляющей. Возьмем задачу разгона сориентированной зерновой частицы в канале треугольного сечения, наклоненном под большим углом к горизонту с целью последующей подачи на гладкую отражательную поверхность, когда после удара она отскакивает на определенное расстояние, зависящее от ее влажности. При этом происходит разделение зерновой массы на фракции различной влажности.

Характеристики канала приведены на рисунке 3.

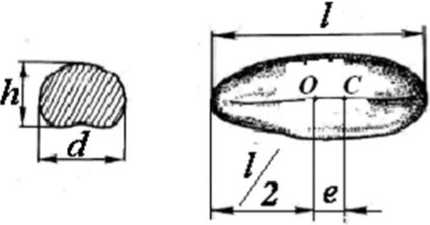
Зерновая частица характеризуется следующими параметрами (рис.4).

Рис. 4. Параметры зерновой частицы: h - высота; d - ширина; l - длина; е = OC - смещение центра масс от геометрического центра

Предварительно зерновая частица ориентируется тяжелой частью вперед по движению и попадает в канал треугольного сечения, где происходит ее разгон, причем сам канал наклонен под большим углом a .

Расчетная схема движения зерновой частицы как материальной точки представлена на рисунке 5.

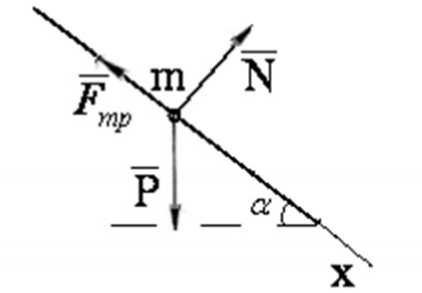
Рис.5. Расчетная схема движения зерновой частицы

Движение такой точки описывается дифференциаль-

ным уравнением второго порядка:

d 2 x

m •     = P • sin a

dt ²

—

, тр ,

где P – вес частицы; х – закон движения; t – время; F _тр –

сила трения; a - угол наклона плоскости.

Однако определение Fтр зависит от положения зер- новой частицы внутри канала. Возможны четыре варианта, представленных на рисунке 6.

а                         б                        в                            г

Рис.6. Схемы расположения зерновой частицы внутри канала

В случае а, б центр тяжести частицы расположен выше, чем в и г, поэтому первые два варианта являются неустойчивым движением. Их следует исключить из рассмотрения и обратиться к последним двум. Случай в представлен на рисунке 7.

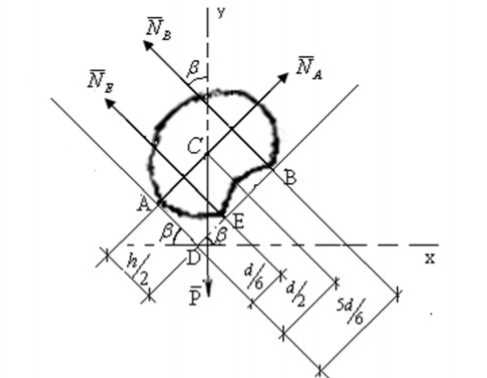
Рис.7. Схема расположения зерновой частицы по варианту в

Здесь А, Е, В – точки контакта с поверхностью канала; точка С – центр масс зерновой частицы.

Движение частицы в этом случае описывается дифференциальным уравнением второго порядка:

d2x m • —2" = P • sin a — FmpA — FmpS — FmpE , (2)

где F _трА – сила трения в точке А; F _трЕ – сила трения в точке Е; F _трВ – сила трения в точке В.

Для определения сил трения необходимо знать нормали в соответствующих точках:

'FmpA = f • Na

(3) трЕ J Е mpB J N B.

Их определим из уравнений равновесия:

Z F KX =0 I F ky = 0;	- N e ■ sin в - NB ■ sin в + N A ■ sin в = 0; N e ■ cos в + NB ■ cos в + N A ■ cos в - P ■ cos a = 0;
Z mD ( F k )=0;	NE ■ — + Nb ■ — d - N, ■ 7 - p ■ cos в ■ — ■ cos a + P ■ sin в ■ — ■ cos a = 0. E 6     B 6       A 2            2                  2

В системе (4) три неизвестные реакции опор N _A , N _B , N _E . Решая совместно уравнения, получим искомые реакции как функции углов a , в :

N e =

N A

- N в + N A ;

P

N B

N Е

=-- cos a ;

2 ■ cos в

3       d     h       Phd

=---- ( P (cos в ---sin в ■ —) ■ cos a +------- (---) ■ cos a );

2 ■ d          2        2         2cos в 2 6

P 3       d     h Phd

=---(P (cos в ■ - sin в ■ —) +-------().

2 ■ cos в  2 ■ d          2        2   2cos в2 6

Приняв угол в =45 0 , нормали будут равны:

N

A

P ■ 72

==------ cos a ;

NB

p ■ 72

==------ cos a ;

N Е

P ■ 72

cos a .

Соответствующие силы трения:

f г P ■ ^V2

F mpA = ^f --2 cos a

P ^

F ■ = f ■ —cos a p ■ 72

^FmpB = ^f ^ 4 cos a

Дифференциальное уравнение для случая в примет вид:

m ■

d—x = P ■ sin a - f ■ P ■ dt ²

72 ■

cos a .

Случай г представлен на рисунке 8.

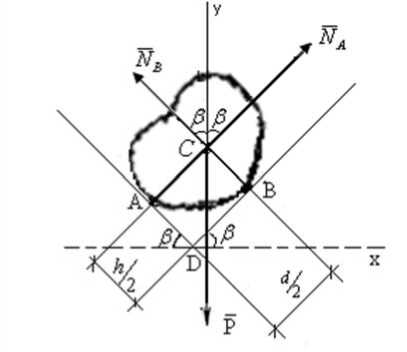
Рис. 8. Схема расположения зерновой частицы по варианту г

Движение частицы в этом случае описывается дифференциальным уравнением второго порядка:

m ■ dX = ^P ■ ^{sin a} - F mpA - F mpB •                 ⁽⁹⁾

Для определения сил трения необходимо знать нормали в соответствующих точках. Аналогично нормали находим из уравнений равновесия:

Z F KY = 0;

Z m D ( F k ) = 0;

N A • cos в + N B • cos в — P • cos a = 0;

dh

N B • 2 ^- N A • ^

dh

- P • cos в у cos a + P • sin в у cos a = 0.

Реакции как функции углов a , в будут:

N

A

Pd

( - d • cos в +      + sm в • h ) • cos a ;

( d + h )             cos в

N

P • cos a cos в

Pd -------( - d • cos в +-- ( d + h )             cos в

+ sin в • h ) • cos a .

При в =45 0 , реакции будут равны:

N

A

P • Л

• •    cos a ;

NB

p • 72 ==----- 2

• •    cos a .

Дифференциальное уравнение (9) примет вид:

d 2 x

m •     = P • sin a - f • P • V2 • cos a .

dt ²

В результате можно сделать вывод, что в случаях в и г расположения зерновых частиц в канале треугольного сечения рифленой направляющей при угле в =45 0 уравнения движения одинаковы. Движение в канале отличается от движения материальной точки по ровной поверхности величиной силы трения. Различие будет в 1,4 раза и зависит от a - угла наклона скатной поверхности.

Проинтегрировав уравнение (13) дважды, подставив начальные условия, получим:

V = V 0 + (sin a - f • 72 • cos a ) • g • t ;

i t2

2 • cos a ) • g • y,

5 = Vj • t + (sin a - f • где V – закон изменения скорости;

S – закон изменения координаты x как функция от времени и угла наклона поверхности.

Величины, полученные при интегрировании дифференциальных уравнений движения в прямолинейном канале треугольного сечения, используются при определении скорости удара об отражательную поверхность и для дальнейшего анализа разделения зерновой массы на фракции различной влажности.

Поверхности отклика скорости движения и длины деки по уравнениям (14) построены в системе Mathcad. Как функции от времени и угла наклона деки они представлены на рисунке 9.

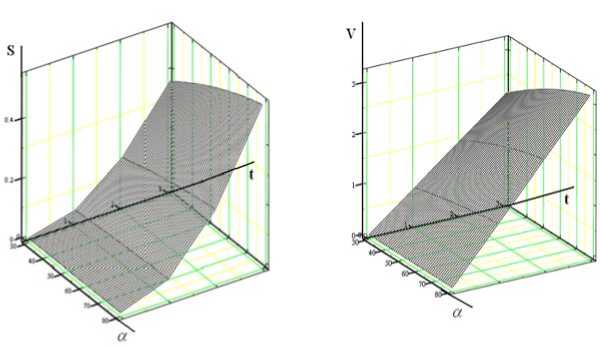
а

б

Поверхности отклика задают зависимость между конструктивными параметрами.

Для численного решения дифференциальные уравнения проинтегрированы в системе Mathcad. Движение зерновых частиц для сравнения рассматривается в канале треугольного сечения и по прямолинейной деке. Углы наклона деки различные. Результаты расчетов, например при углах a =30⁰,35⁰ при длине деки 30 см, представлены на рисунках 10, 11.

Угол наклона деки 35°

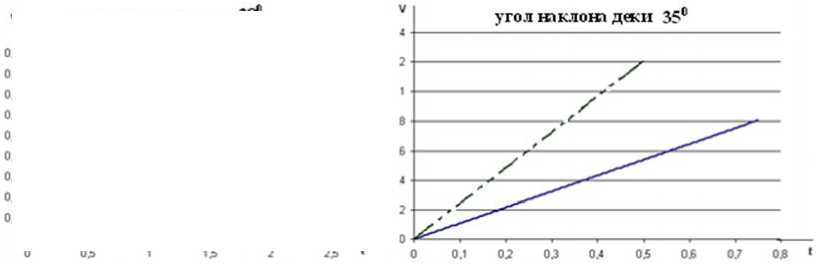
- канал треугольного сечения

^^^^^^^^^^^^^^^^^^^^^

_ - прямолинейная дека

Угол наклона деки 30°

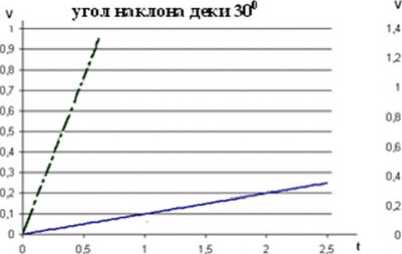
Рис.10. График изменения скорости частиц по времени

Угол наклона 30°                           Угол наклона 35°

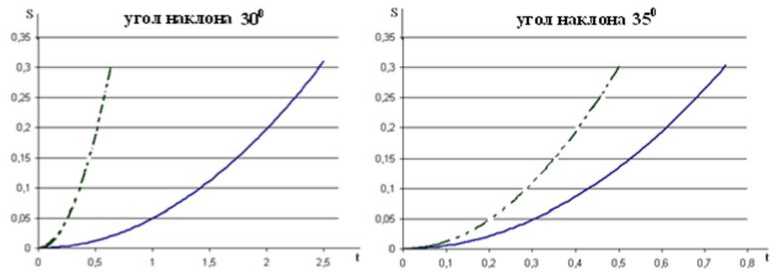
- канал треугольного сечения - прямолинейная дека

Рис.11. График изменения перемещения по времени

На рисунках 12, 13 представлены перемещения частиц зернового материала по наклонному каналу треугольного сечения и по прямолинейной деке в зависимости от угла наклона к горизонту.

Перемещение зерновых частиц в канале треугольного сечения в зависимости от угла наклона деки

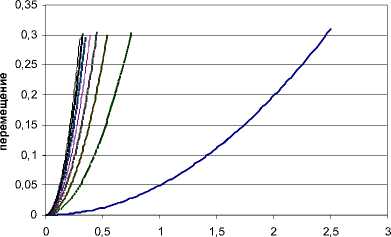
Время

30 градусов

35 градусов

40 градусов

45 градусов

50 градусов

55 градусов

60 градусов

65 градусов

Рис.12. График изменения перемещения по каналу треугольного сечения

Перемещение зерновых частиц по прямолинейной поверхности в зависимости от угла наклона деки

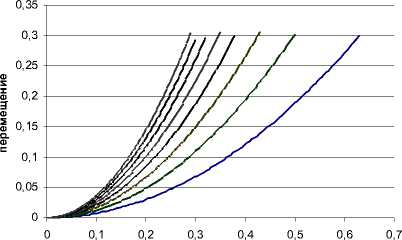
Время

30 градусов 35градусов

40 градусов

45 градусов

50 градусов

55 г радусов

60 градусов

65 градусов

Рис.13. График изменения перемещения по прямолинейной деке

На рисунках 14,15 представлены графики изменения скоростей частиц зернового материала по наклонному каналу треугольного сечения и по прямолинейной деке в зависимости от угла наклона к горизонту.

Скорость зерновых частиц в канале треугольного сечения в зависимости от угла наклона деки

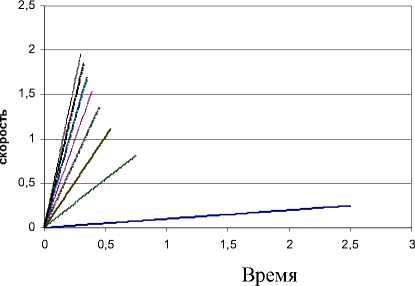
30 градусов

35 градусов

40 градусов

45 градусов

50 градусов

55 градусов

60 градусов

65 градусов

Рис.14. График изменения скорости по каналу треугольного сечения

Скорость зерновых частиц по прямолинейной поверхности в зависимости от угла наклона деки

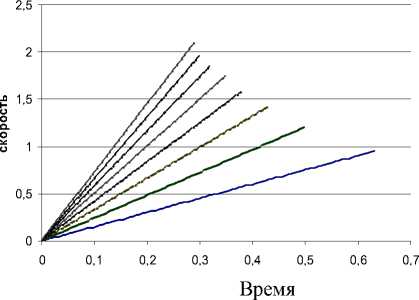
30 градусов 35градусов

40 градусов

45 градусов

50 градусов

55 г радусов

60 градусов

^^™ ^^м 65 градусов

Рис.15. График изменения скорости по прямолинейной деке

Таким образом, можно сделать следующий вывод: ориентированное движение частиц в канале треугольного сечения рифленой деки отличается от движения по гладкой наклонной поверхности отсутствием вращательных составляющих движения, т.е. оно сопоставимо с движением материальной точки.

Движение частиц в канале треугольного сечения отличается от движения материальной точки по ровной поверхности при одинаковых углах наклона к горизонту величиной силы трения.

Минимальный угол наклона, при котором возможно движение частиц зернового материала в канале, – 300. При меньшем угле наклона прямолинейного канала треугольного сечения движение частиц не происходит.

На графиках видно, что время движения частиц по каналу треугольного сечения больше по сравнению с прямолинейной поверхностью, скорость на выходе – меньше. Но преимущество в том, что движение частиц является стабилизированным, отсутствует вращение, кинематические характеристики частиц будут одинаковы. Необходимую же скорость частиц на выходе с рифленой деки можно подобрать, изменяя угол ее наклона и длину. Это будет связано с дальнейшими исследованиями по отскоку зерновых частиц от отражательной поверхности на определенное расстояние, зависящее от влажности.