Теоретико-графовое приведение реляционной базы данных к третьей нормальной форме Э.Кодда

Приведение базы данных к третьей нормальной форме (3НФ) является одним из наиболее часто используемых аспектов теории реляционных БД. При этом, алгоритм приведения БД к 3НФ является скорее интуитивным, что не позволяет использовать его для автоматизированного проектирования базы данных.

На настоящий момент приведение БД к 3НФ осуществляется программистом по его собственному усмотрению, а это, в свою очередь приводит зачастую к потере качества и, кроме того, существенно увеличивает продолжительность разработки. Фактически, нормализация БД сейчас, если ее строго формализовать, сводится к полному перебору всех возможных вариантов декомпозиции множества полей таблиц БД на подмножества, удовлетворяющие 3НФ.

Конечно, опытный программист зачастую уже интуитивно разбивает БД правильно, однако, не все программисты являются опытными. Кроме того, даже у сильного программиста приведение реальной БД к 3НФ занимает как минимум час, а максимальное время может затянутся и на 2-3 рабочих дня. При этом, в случае необходимости изменения БД из 100-150 таблиц (например, при появлении новых функциональных требований в процессе эксплуатации), приходится проектировать структуру заново. Даже автоматизация этого процесса не сильно помогает, потому что, к сожалению, автоматизация полного перебора в случае 100-150 таблиц по 5-10 полей в каждом (итого около 1000 единиц), каждое из которых надо сравнить с оставшимися, занимает непозволительно долгое время.

В результате, огромное количество даже реально работающих БД имеют ненормализованную структуру, а зачастую (особенно в государственных предприятиях с традиционно низким уровнем компьютерной грамотности) – просто представляют собой одну большую таблицу, содержащую все данные. Естественно, такой подход к хранению данных крайне избыточен, «быстрый» поиск в такой БД практически невозможен, да и организовать нормальную работу пользовательского интерфейса для такой БД – задача крайне трудоемкая.

Для эффективной и быстрой нормализации реляционной базы данных необходимо применять не интуитивный, а формализованный математический подход. Он позволил бы автоматизировать процесс нормализации реляционной БД, что в свою очередь, сократило бы время проектирования БД с нескольких часов до нескольких минут. В данной работе автором предложен алгоритм декомпозиции ненормализованной таблицы в таблицы, находящиеся в 3НФ, т.е. приведения базы данных к 3НФ.

Прежде всего, для понимания данного алгоритма, необходимо вернуться к предложенному Э. Коддом термину «отношение», описывающему взаимодействие между двумя полями таблицы, при котором значение одного из полей однозначно характеризует другое. Например, номер ИНН однозначно указывает на конкретного сотрудника предприятия. То есть, имея доступ к БД предприятия и зная ИНН, можно получить всю остальную информацию по сотруднику. Тогда как знание, например, фамилии сотрудника не принесет нам точной информации, поскольку в рамках одного предприятия могут найтись однофамильцы.

В более широком смысле в качестве такого значения (оно также называется «ключевым») может выступать совокупное значение набора полей (например, серия и номер паспорта в совокупности однозначно определяют гражданина РФ) (табл. 1).

Табл. 1. Таблица «Сессия»

№ зачетки	ФИО студента	Группа	Предмет	№ предмета	ФИО преп.	№ удост. Преп.	Дата	Оцен ка	Факу льте т
134543	Иванов И.А.	АСП-1	Дискр. Матем.	53213	Горбатов В.А.	543212	15.06.0 9	4	АИ
545313	Петров А.В.	АСП-1	Дискр. Матем.	53213	Горбатов В.А.	543212	15.06.0 9	5	АИ
123453	Сидорова О.М.	АСП-2	ЯВУ	54345	Смагина И.А.	359482	15.06.0 9	3	АИ
123534	Киселева О.Я.	АСП-2	ЯВУ	54345	Смагина И.А.	359482	15.06.0 9	5	АИ
134543	Иванов И.А.	АСП-1	ЯВУ	54345	Смагина И.А.	359482	21.06.0 9	4	АИ
545313	Петров А.В.	АСП-1	ЯВУ	54345	Смагина И.А.	359482	21.06.0 9	3	АИ
123453	Сидорова О.М.	АСП-2	ОТУ	54123	Певзнер Л.Д.	948345	10.06.0 9	2	Аи
123534	Киселева О.Я.	АСП-2	ОТУ	54123	Певзнер Л.Д.	948345	10.06.0 9	4	АИ

Между полями данной таблицы существует набор отношений, т.е., значение одного поля однозначно определяет значение другого поля (например, № зачетки однозначно определяет значение полей «ФИО студента», «Группа», «Факультет»).

Однако все отношения между таблицами являются сугубо «мысленными», т.е., таблица никак не показывает, что между ее столбцами есть какое-то взаимодействие, хотя Э.Кодд прямо определил наличие отношений между столбцами таблицы в БД. Отношения между столбцами таблицы известны только программисту, а значит, нормализация такой системы неформализуема, т.е. не поддается автоматизации. Для формализации отношений между полями в таблице необходим подход, который бы отобразил эти отношения. И как нельзя лучше здесь приходится графовый анализ.

Графовая интерпретация данной таблицы изображена на рис. 1. Направление дуги от вершины b к вершине a указывает, что вершина b однозначно определяется вершиной a. Множество вершин V (V к , V н ) является двусортным. Вершины с кодом 1 называются ключевыми , т.е. соответствующие им столбцы входят в первичный ключ данной таблицы. Вершины с кодом 0 называются неключевыми . Для удобства вершины с кодом 1 обозначим черным цветом, а вершины с кодом 0 – белым. Кроме того, каждая вершина взвешена номером той таблицы, в которую входит соответствующий ей столбец (на настоящий момент все вершины взвешены номером 1, т.к. БД состоит из одной таблицы).

Электронное научное издание «Устойчивое инновационное развитие: проектирование и управление»

Вершины графа G соответствуют следующим столбцам табл. 1:

A - № зачетки, b – ФИО студента, c – Группа, d – предмет, e - № предмета, f – ФИО преподавателя, g - № удост. преп., h – дата экзамена, i – Оценка, j – факультет. Вершины a, e, h являются ключевыми, т.к. соответствующие им поля таблицы образуют составной первичный ключ данной таблицы.

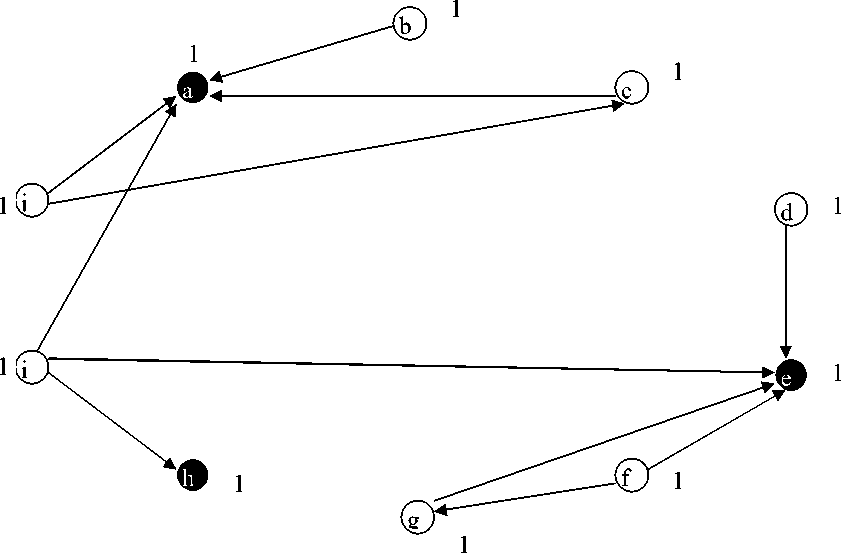
Рис. 1. Граф G

Для нормализации моделируемой БД необходимо последовательно привести ее к 1НФ, 2НФ, 3НФ. Приведение БД к 1НФ представляется абсолютно неформализуемой задачей, поскольку полностью диктуется предметной областью. Те или иные значения полей в одной задаче могут быть атомарными, а в другой – нет, поэтому, приведение БД к 1НФ оставим полностью «на совести» исполнителя. Табл. 1 будем считать уже приведенной к 1НФ.

Для соответствия 2НФ БД должна быть в 1НФ и, при этом, все неключевые поля должны функционально полно зависеть от ключевых полей. Иными словами не должно быть такой пары вершин v 1 єV к , v 2 єV н , для которой не существовало бы отношения v 1 →v 2 (1). В случае, если такие пары вершин находятся, они должны быть выделены в отдельные подграфы.

В результате операции приведения графа G к 2НФ, граф разбивается на N подграфов, для каждого из которых (1) справедливо. При этом, количество подграфов должно стремиться к минимуму.

Построим двумерную таблицу (табл. 2.), строкам которой будут соответствовать неключевые вершины, а столбцам все возможные наборы ключевых вершин. Набор соответствует комбинации ключевых вершин. В ячейке таблицы ставится 1, если неключевая вершина соответствующая строке связана с неотрицательными ключевыми вершинами набора, соответствующего столбцу. В противном случае, в ячейке ставится 0. Связи между неключевыми вершинами в графе на данном этапе не учитываются.

Табл. 2. Матрица 2НФ

	aeh	aeh	aeh	aeh	aeh	aeh	aeh	aeh
b	1	0	0	0	0	0	0	0
c	1	0	0	0	0	0	0	0
d	0	1	0	0	0	0	0	0
g	0	1	0	0	0	0	0	0
f	0	1	0	0	0	0	0	0
i	0	0	0	0	0	0	1	0
J	1	0	0	0	0	0	0	0

Удалим из указанной таблицы все столбцы, содержащие только 0. Это ключевые наборы, не порождающие новых таблиц (табл. 3.).

Табл. 3. Матрица 2НФ

	aeh	aeh	aeh
b	1	0	0
c	1	0	0
d	0	1	0
g	0	1	0
f	0	1	0
	aeh	aeh	aeh
i	0	0	1
J	1	0	0

Теперь «склеим» строки в данной таблице, фиксируя состав каждой строки (табл. 4.).

Электронное научное издание «Устойчивое инновационное развитие: проектирование и управление»

Табл. 4. Матрица 2НФ

	aeh	aeh	aeh
1	1	0	0
2	0	1	0
3	0	0	1

Строка 1 = { a,b,c,j }

Строка 2 { e,d,g,f }

Строка 3 { a,e,h,I }

Единица в ячейке данной таблицы означает отдельный подграф, моделирующий отдельную, приведенную к 2НФ таблицу. При этом, в получившихся таблицах образуются новые ключевые последовательности, являющиеся частью ключа табл. 1. Между этими новыми ключами и соответствующими им частями ключа из табл. 1 устанавливается связь, направленная от исходного графа к производному. При этом, каждый подграф взвешивается

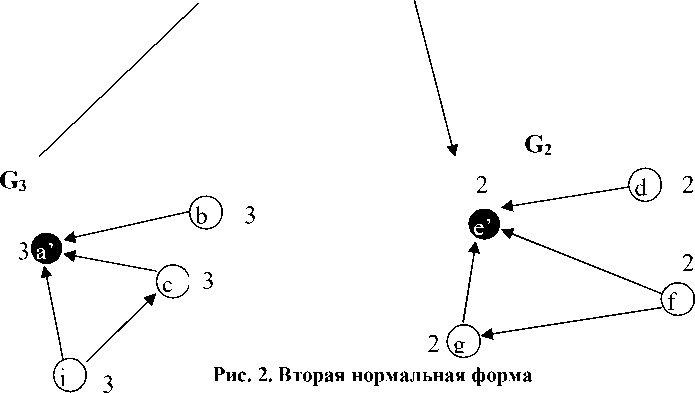
Как видно из рис. 2, граф исходный G преобразован в граф G2НФ, состоящий из трех подграфов: G1 (сессия), G2 (предметы), G3 (студенты). Вершины, входящие в указанные е расщеплены. Так,

графы, взвешены соответс вершина а в графе G1 входит в состав первичного ключа, а в графе G3 вершина а’ является сама по себе первичным ключом. При этом, между этими вершинам образуется отношение – значение поля a из таблицы 1 однозначно определяется значением поля а’ из таблицы 3. По аналогии построен граф G2.

В соответствии с теорией реляционных БД, для приведения графа к 3НФ необходимо сначала привести его к 2НФ, а затем устранить зависимости неключевых полей друг от друга. Т.е., не должно быть такой пары вершин v 1 єV н , v 2 єV н , для которой существовало бы отношение v 1 →v 2 (2). Задача приведения представленной системы к 3НФ сводится к разбиению графов данной системы на такие графы, для которых условие 2 справедливо.

Приведение к 3НФ осуществляется похожим алгоритмом. Только, для анализа используются связи между неключевыми вершинами.

Рассмотрим матрицу 3НФ, строкам которой соответствуют неключевые вершины, а столбцам – возможные наборы их связей (табл. 5.).

Табл. 5. Матрица 2НФ

	8	с
f	1	0
J	0	1

В таблице 5 для скорости анализа удалены «нулевые» строки и столбцы. Данная таблица «отщепляет» два графа от графов (2) и (3). Взвесим вершины образовавшихся графов цифрами 4 и 5. 1

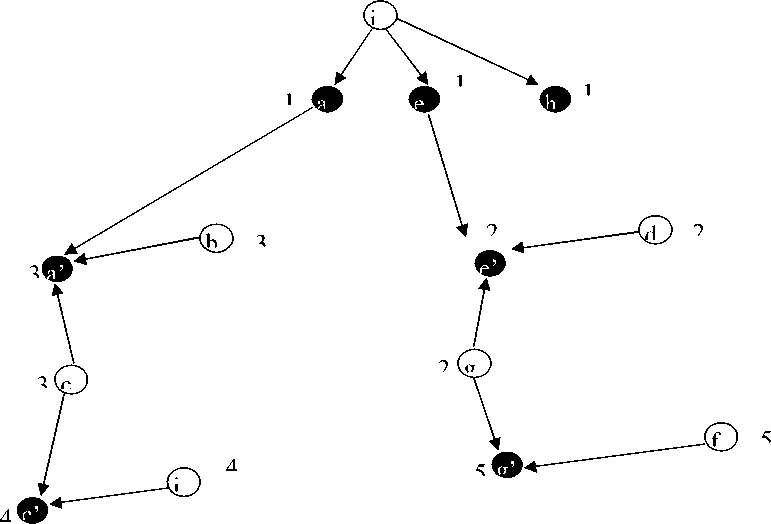
Рис. 3. Третья нормальная форма

В результате образования новых подграфов может случиться, что какой-либо из них окажется не приведенным к 2НФ или 3НФ. В этом случае к нему применяется этапы, описанные выше до тех пор, пока вся система не окажется разбитой на подграфы, приведенные по отдельности к 3НФ.

В результате графового анализа предложенной БД, получим разбиение ненормализованной таблицы на следующий набор таблиц, приведенных к 3НФ:

Табл. 6. Таблица «Экзамены»

№ зачетки	№ предмета	Дата	Оценка
134543	53213	15.06.09	4
545313	53213	15.06.09	5
123453	54345	15.06.09	3
123534	54345	15.06.09	5
134543	54345	21.06.09	4
545313	54345	21.06.09	3
123453	54123	10.06.09	2
123534	54123	10.06.09	4

Табл. 7. Таблица «Студенты»

№ зачетки	ФИО студента	Группа
134543	Иванов И.А.	АСП-1
545313	Петров А.В.	АСП-1
123453	Сидорова О.М.	АСП-2
123534	Киселева О.Я.	АСП-2

Табл. 8. Таблица «Предметы»

Предмет	№ предмета	№ удост. Преп.
Дискр. Матем.	53213	543212
ЯВУ	54345	359482
ОТУ	54123	948345

Табл. 9. Таблица «Группы»

Группа	Факультет
АСП-1	АИ

Табл. 10. Таблица «Преподаватели»

ФИО преп.	№ удост. Преп.
Горбатов В.А.	543212
Смагина И.А.	359482
Певзнер Л.Д.	948345

При решении задач по нормализации баз данных преимущества использования формализованного алгоритма перед интуитивным очевидны. Снижается влияние человеческого фактора, ускоряется работа, решение задачи становится наглядным и понятным даже для несвязанного с предметной областью человека. По сути, такой строгий математический подход позволяет разделить работу на два этапа:

А) Формирование первичного графа (выполняется специалистом по предметной области);

Б) Последующая нормализация полученного графа (выполняется разработчиком).

В этой ситуации количество ошибок при разработке структуры данных, которая является ключевой составляющей любой информационной системы, снижается в разы, поскольку каждый занимается работой исключительно в своей области.

Использованный в данном примере алгоритм является точным, т.е., он основан не на домыслах программиста, а исключительно на точном математическом анализе графа БД. Кроме того, данный алгоритм полностью оторван от предметной области (она используется только при построении самого графа БД), что позволяет использовать его при решении практически любой задачи по нормализации графа. Кроме того, формализованный алгоритм, в отличие от интуитивного, вполне можно автоматизировать. А учитывая отхождение от полного перебора, вполне можно добиться от полученной программы достаточно высокой скорости работы, т.е., серьезно сократить время разработки и переработки программы.

Таким образом, на основании вышеизложенных принципов, можно определить следующий алгоритм приведения таблицы к 3НФ.

• 1.    БД вручную приводится к 1НФ. Для этого все поля таблицы приводятся к атомарному виду.

• 2.    На основании полученной на этапе 1 таблицы строится орграф G, в котором вершины соответствуют столбцам таблиц, а дуги – отношениям между этими таблицами. При этом, вершины, обозначающие ключевые поля, называются ключевыми , а вершины, обозначающие неключевые поля – неключевыми .

• 3.    Строится матрица 2НФ, строкам которой соответствуют неключевые вершины, а столбцам все возможные наборы ключевых вершин. В случае, если i-я вершина зависит от J-го набора, в ячейке [I,j] ставится 1, в противном случае – 0.

• 4.    Из матрицы 2НФ удаляются столбцы, содержащие только 0 (т.е. не порождающие ни одной таблицы).

• 5.    В матрице 2НФ склеиваются одинаковые строки с фиксацией вхождения строк исходной таблицы в строки новой таблицы.

• 6.    Каждая единица, полученная в матрице 2НФ представляет собой подграф, приведенный к 2НФ.

• 7.    В случае, если какие-то из полученных подграфов не являются приведенными к 2НФ, к ним снова применяются шаги 3-6 до тех пор, пока все подграфы графа G не будут приведены к 2НФ. Полученный граф называется G 2НФ .

• 8.    Строится матрица 3НФ, строкам которой соответствуют неключевые вершины, а столбцам все возможные наборы соединенных между собой неключевых вершин. В случае, если i-я вершина зависит от J-го набора, в ячейке [I,j] ставится 1, в противном случае – 0.

• 9.    Из матрицы 3НФ удаляются столбцы, содержащие только 0 (т.е. не порождающие ни одной таблицы).

• 10.    В матрице 3НФ склеиваются одинаковые строки с фиксацией вхождения строк исходной таблицы в строки новой таблицы.

• 11.    Каждая единица, полученная в матрице 3НФ представляет собой подграф, приведенный к 3НФ.

• 12.    В случае, если какие-то из полученных подграфов не являются приведенными к 3НФ, к ним снова применяются шаги 8-11 до тех пор, пока все подграфы графа G 2НФ не будут приведены к 3НФ. Полученный граф называется G 3НФ .

Предложенный алгоритм является формализованным, он не привязан к предметной области. При этом предложенный алгоритм позволяет применить к процессу нормализации средства автоматизации, т.е. разработать программное средство, автоматизирующее этот процесс.