Теоретико-графовые модели с упорядоченной иерархической структурой и их использование в анализе синтаксиса поэтических текстов

В математике и информатике графы являются удобным механизмом представления информации. Однако во многих приложениях (например, при моделировании синтаксической структуры текстов) требуются более сложные теоретикографовые модели, обладающие иерархической структурой. Известны иерархические графы и иерархические графовые модели, описание которых приводится в [6; 399–408], однако они не в полной мере подходят для анализа текстов. Поэтому возникает потребность в разработке новых моделей и методов их исследования.

Дадим рекурсивное определение теоретико-графовой модели с упорядоченной иерархической структурой: это пятерка G = (V, W, E, α, β), в которой V = {v,}n - непустое конечное упорядоченное множество вершин; W = {v0 и{ Gj} m } -объединение подмножества вершин V0 с V и множества вложенных теоретико-графовых моделей Gj = (Vj, Wj,Ej, aj, ej), таких что Vj попарно не пересекаются и их объединение совпадает с V \ V0; E с W x W - множество ребер; a : V ^ LV - функция, задающая метки вершинам; в : E ^ LE - функция, задающая метки ребрам, где LV и LE – множества меток и атрибутов объектов и отношений, определенные в некоторой предметной области (номера элементов включаются в состав их меток). Таким образом, внутри теоретико-графовой модели с упорядоченными узлами существует иерархия вложенных друг в друга подструктур, причем ребра могут соединять как обычные узлы, так и вложенные подструктуры, находящиеся на данном уровне вложенности. На рис. 1 показан пример подобной модели, которая подробно описана в [10].

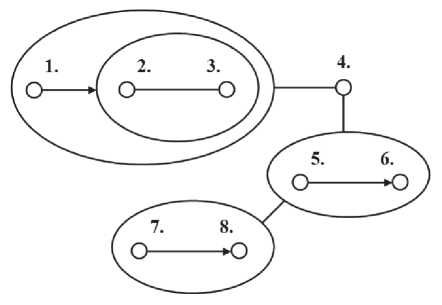
Рис. 1. Пример иерархической теоретико-графовой модели синтаксической структуры предложения «Их гений мужествен, как гений вод твоих…» [3; 83]

В данной работе рассматриваются модели синтаксической структуры многочленных сложных предложений из творчества П. А. Вяземского и И. А. Бродского. Выбор творчества этих поэтов не случаен: именно интеллектуальность поэзии, ее глубина стали отличительной чертой их творчества; стремление к выстраиванию причинно-следственных, глубинных связей, нехарактерное для лирических произведений в целом, отразилось в творчестве этих авторов. Значительную роль в оформлении интеллектуальности и сверхсодержательности поэзии П. А. Вяземского и И. А. Бродского сыграли сложные предложения.

ТЕОРЕТИКО-ГРАФОВАЯ МОДЕЛЬ СИНТАКСИЧЕСКОЙ СТРУКТУРЫ

СЛОЖНОГО ПРЕДЛОЖЕНИЯ

Сложное предложение в современной лингвистике является объектом пристального научного интереса. Одна из немаловажных проблем, актуальных для данной сферы исследования,– типологизация сложных предложений, описание их структуры и составляющих. Исследователи-грамматисты отмечают, что «трудности, с которыми сталкивается синтаксическая наука при решении проблем типологии сложного предложения, начинаются уже на первых этапах классификации» [8]. В связи с этим ощущается потребность в создании некоего механизма, позволяющего размечать сложные предложения с точки зрения их структуры, что облегчило бы последующий анализ, установление взаимосвязей между частями предложения, а также определение роли того или иного сложного предложения в тексте произведения или в целом в творчестве писателя. Сложные предложения в стихотворных произведениях могут рассматриваться, с одной стороны, как показатель той эпохи, к которой принадлежит творчество поэта (очевидно, что со временем синтаксическая структура текстов меняется), а с другой стороны, – как проявление идиостиля писателя [7].

В современной теории синтаксиса широко используются так называемые деревья зависимостей и деревья составляющих [4]. Одним из первых их применил А. М. Пешковский [11] для изображения сочинительных и подчинительных связей между словами. Суть деревьев зависимостей сводится к следующему: считается заданным анализ предложения, устанавливающий подчинительные связи между словами согласно правилам традиционной грамматики и грамматики зависимостей. Результаты анализа представляются в виде графов, вершины которых соответствуют словам, а дуги соединяют их в соответствии с синтаксическими связями. В терминах деревьев зависимостей можно выражать многие стилистические характеристики текстов [12].

Деревья зависимостей обычно используются в описаниях языков со свободным порядком слов (например, русского). Для описания языков с фиксированным порядком слов преимущественно используется второй тип графов – деревья составляющих [4]. При этом в предложении выделяются группы слов, функционирующие как отдельные синтаксические единицы, – составляющие. Система составляющих – это множество отрезков предложения, которое обладает тем свойством, что каждые два входящих в него отрезка либо не пересекаются, либо один из них содержится в другом. При графическом изображении система составляющих тоже приобретает вид дерева.

В качестве модели представления структуры сложного предложения нами была выбрана вертикальная структурная схема. По филологической традиции, вертикальные структурные схемы используются в рамках выполнения синтаксического разбора многочленных сложных предложений. С ее помощью можно понаблюдать расположение предикативных частей, средства связи между ними, а также направление зависимостей между частями сложного предложения. Вертикальная схема удобна в силу того, что не теряется наглядность направления связей (может быть продемонстрирован уровень глубины соотношения блоков внутри многокомпонентных сложных предложений). Вертикальная схема является оптимальным вариантом для представления тех сложных предложений, которые состоят из четырех и более компонентов. В некоторых случаях в качестве компонента сложного предложения может выступать блок, который объединяет несколько тесно связанных между собой частей. Внутри такого блока при более подробном анализе также можно выстроить систему связей (рис. 2). Обозначим сочинительные связи с помощью прямых линий, подчинительные связи – с помощью стрелок, ведущих от главной части к придаточной.

1Во мне идет с ожесточеньем Борьба враждебных двух начал: 2Ум не скудеет размышленьем, 3Но воли нет, 4но дух упал.

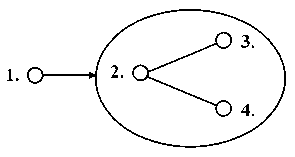
Рис. 2. Теоретико-графовая модель предложения «Во мне идет с ожесточеньем…» [3; 411]

Таким образом, теоретико-графовая модель представляет собой иерархическую структуру с несколькими уровнями вложенности. При этом типы связей делятся на три класса в зависимости от вида союза и характера отношений между частями сложного предложения:

• A.    Сложносочиненные предложения (ССП);

• B.    Сложноподчиненные предложения (СПП);

• C.    Бессоюзные предложения (БСП).

В свою очередь, классы делятся на подклассы типов связей (18 – для ССП, 14 – для СПП и 11 – для БСП). Рассмотрим пример из творчества И. Бродского [2; 80–81], теоретико-графовая модель которого изображена на рис. 3 (слева вверху):

• ¹И бо, ²когда расстаются двое,

• ³т о, перед тем как открыть ворота, ¹каждый берет у другого что-то в память о том, ⁴как их век был прожит: ⁵тело – незримость; ⁶душа, быть может, зренье и слух.

Здесь выделяются следующие типы связей (пятая связь соединяет две вложенные подструктуры):

• 1→ 2: СПП с придаточным времени (BF);

• 1→ 3: СПП с придаточным времени (BF);

• 3→ 4: СПП с придаточным изъяснительным (BC);

• 5– 6: БСП со значением перечисления (CA);

[1–4]–[5–6]: БСП со значением пояснения (CD).

ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКИХ

МЕТОДОВ ДЛЯ СРАВНИТЕЛЬНОГО АНАЛИЗА ТЕОРЕТИКО-ГРАФОВЫХ МОДЕЛЕЙ

Для сравнения и классификации теоретикографовых моделей можно применить несколько подходов [9]. Одним из них является вычисление числовых характеристик, отражающих структурные особенности графов. В простейшем случае это параметры размерности – число вершин и ребер графа. К более сложным параметрам можно отнести параметр глубины (число уровней в дереве), параметр ширины (наибольшее число узлов на уровне), коэффициент асимметрии (логарифм отношения количества узлов, расположенных слева от корня, к количеству узлов, расположенных справа от корня), веточный параметр (отношение числа концевых узлов к числу уровней глубины), параметр вложенности (максимальная степень вложенности структур друг в друга) и др.

Второй подход основан на введении метрики на множестве графов. Здесь задается мера, которая позволяет оценить, насколько те или иные структуры «похожи» друг на друга. В зарубежной литературе данное направление получило название « graph matching » [13]. К подобным способам оценки сходства графов относится мера на основе операций редактирования ( graph edit distance ). Эта мера является расширением известного правила сравнения строк Вагнера – Фишера [14]. Здесь строится минимальная последовательность операций редактирования (как правило, это добавление, удаление или переименование вершин и ребер), которая преобразует одну теоретико-графовую модель в другую. При этом на практике часто одни операции являются более значимыми по сравнению с другими, поэтому каждой операции ставится в соответствие ее положительный вес γ : ∑→ R ⁺ , где ∑ – множество операций редактирования. Расстояние вычисляется как минимальная по сумме весов последовательность операций редактирования, преобразующая одну модель в другую.

В данном исследовании был рассмотрен алгоритм нахождения расстояния, который является модификацией алгоритма Вагнера – Фишера нахождения расстояния между строками. Для представления графа в виде строки каждой вершине (простому предложению в составе сложного в порядке следования) ставятся в соответствие следующие параметры (рис. 3):

• 1.    Тип связи между этим предложением и родительским (в силу древоподобной структуры такая связь всегда одна или ее нет для корневых элементов);

• 2.    Ссылка на порядковый номер родительского элемента;

• 3.    Уровень вложенности (равный нулю для внешних узлов структуры и увеличивающийся на единицу для всех вложенных подструктур). Вложенная подструктура на последующем уровне вложенности ведет себя как обычный узел, то есть может иметь входящие и исходящие связи; в то же время она всегда имеет корень, у которого отсутствует непосредственный родительский узел.

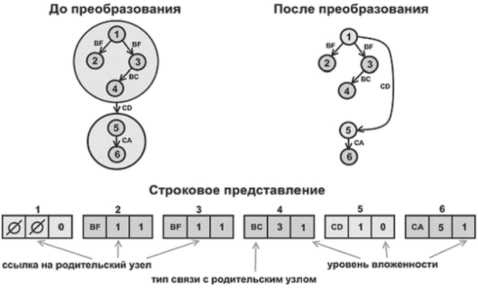
Рис. 3. Строковое представление теоретико-графовой модели

Таким образом, вычисление стоимости операций проводилось не только в зависимости от меток узлов, но и при помощи функций от таких параметров, как уровень вложенности и связь с другими узлами. Заметим, что операции редактирования, изменяющие уровень вложенности узлов, являются недопустимыми, что позволяет вычислять расстояния для всех уровней вложенности за одну итерацию алгоритма, без рекурсии.

Заметим, что определенное таким образом расстояние удовлетворяет условиям метрики [14]:

• 1.    d ( G , , G 2 ) >  0 (неотрицательность): выполняется, поскольку сумма положительных весов является положительным числом;

• 2.    d ( G , , G 2 ) = 0 О G , = G ₂ ;

• 3.    d ( G , , G ₂) = d ( G ₂, G , ) (симметричность): обратная последовательность операций редактирования, преобразующая G ₂ в G ₁ , совпадает с исходной и имеет тот же суммарный вес;

• 4.    d ( G , , G ₂) <  d ( G , , G ₃) + d ( G ₃, G ₂) (неравенство треугольника): расстояние d ( G ₁, G ₂) определяется как минимальная по стоимости последовательность операций, преобразующая структуру G 1 в структуру G 2 . Значит, любая последовательность, преобразующая структуру G ₁ в G ₃ , а затем G ₃ в G ₂ (то есть с заданным промежуточным состоянием), по определению имеет не меньшую стоимость, чем d ( G ₁, G ₂) .

Алгоритм Вагнера – Фишера заключается в последовательном заполнении матрицы m х n промежуточными значениями расстояний, вычисляемых по формуле:

max(z,y)

z = О или j = О

D(i, j) = < min(D(z,y-l) + l,D(z-l,y) + l,

D(z-l,y-l) + Z(S,[aS2[y])); z = 1, ...,m,j = 1, ...,n где /(S,[i],S2[j]) - функция стоимости замены элемента S1[i] на S2 [j], и равна нулю, если эти элементы идентичны, m и n – количество простых элементов в G1 и G2 соответственно. В матрице шаг по i символизирует удаление элемента из первой строки, по j – вставку в первую строку, а шаг по обоим индексам одновременно символизирует замену элемента или отсутствие изменений, если элементы равны.

Для определения степени схожести типов синтаксических связей совместно с экспертами-филологами была построена матрица C разме- ром 43 × 43 со значениями от 0 до 1. Вопросы, связанные с синкретизмом сложных предложений, промежуточными видами между типами и видами сложных предложений, входят в сферу интереса филологов [1], [5]. В рамках данного исследования невозможно провести полный и обстоятельный анализ трансформации между разными типами связи с привлечением большого числа примеров и контекстов, однако вместе с тем в основу таблицы коэффициентов положены определенные выводы, связанные с анализом структуры различных сложных предложений. В связи с этим были рассмотрены два вопроса: 1) трансформация одной связи в другую в пределах одного класса; 2) трансформация для связей разных классов.

Для элементов одного уровня стоимость операции редактирования мы определяем по формуле:

(a, b) =, - C [ a, b ] ■ l (a, b), где C[a, b] – степень схожести типов синтаксических связей a и b; l(a,b) – функция со значениями от 0 до 1, принимающая значение 1, если родительский элемент не меняется (не производится перенос элемента), и значение меньше 1, если родительский элемент a не равен родительскому элементу b. В этом случае мы можем либо определить значение как 0, либо сделать его зависимым от расстояния, на которое узел переносится. Для этого была выбрана функция следующего вида:

l ( a , b ) = const ■ \inkk_a - link b |, где | link_a - link b | - модуль разницы между номерами родительских узлов, а const – константа от 0 до 1 (в нашем случае взята 0,5), характеризующая гибкость данной метрики относительно переносов узлов на небольшие расстояния.

В результате исследования была построена выборка из 61 предложения из творчества П. А. Вяземского, 57 предложений И. А. Бродского и их теоретико-графовых моделей. В результате работы алгоритма была построена матрица расстояний размером 118 × 118. Эту матрицу можно использовать, например, для выявления возможной зависимости расстояний между структурами предложений от авторства этих предложений. На рис. 4 представлена диаграмма средних значений и отклонений расстояний: между всеми предложениями выборки (a), только между предложениями П. А. Вяземского (b), только между предложениями И. А. Бродского (c) и перекрестное расстояние между предложениями П. А. Вяземского и И. А. Бродского (d). Здесь средние значения представлены точками в центре отрезков, характеризующих среднее отклонение расстояний.

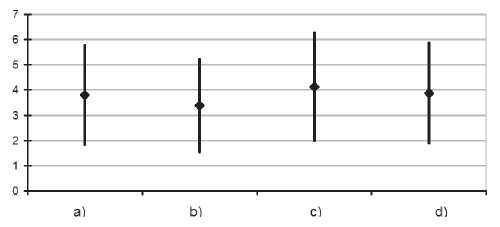
Рис. 4. Расстояния между всеми предложениями

Кроме того, было проведено исследование расстояния между предложениями с достаточно сложной структурой, которые содержали более чем 4 части. В результате получилась диаграмма, изображенная на рис. 5.

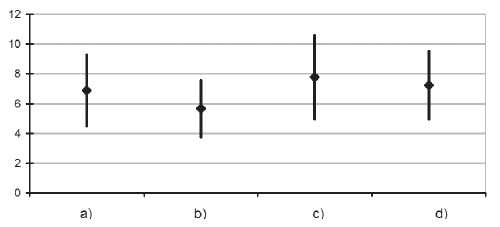
Рис. 5. Расстояния между предложениями с более чем 4 частями

Как видно, значения расстояний между предложениями в случаях (b) и (с) заметно отличаются друг от друга, причем это отличие проявляется более ярко для предложений с достаточно сложной структурой. Можно сделать предположение, что И. А. Бродский использовал более широкий спектр синтаксических структур предложений, чем П. А. Вяземский, причем это разнообразие структур становится заметнее с увеличением степени сложности предложения. Для проверки этой гипотезы необходимо сравнить расстояния для других выборок предложений из стихотворений тех же авторов, кроме того, интерес представляет изучение других способов определения расстояний между моделями предложений.

ЗАКЛЮЧЕНИЕ

В данной статье рассмотрены теоретикографовые модели с упорядоченной иерархической структурой и методы их сравнительного анализа. Апробация алгоритмов проводилась на моделях синтаксической структуры сложных предложений из творчества П. А. Вяземского и И. А. Бродского. В ходе исследования была обнаружена заметная зависимость значений расстояний между предложениями от их авторства. Зависимость выражается сильнее при сравнении больших предложений с нетривиальной структурой. Относительно большое внутреннее расстояние между предложениями И. А. Бродского означает большее разнообразие между структурами предложений и, вероятно, говорит о разнообразии и непостоянстве авторского стиля. Относительно малое расстояние между предложениями П. А. Вяземского, напротив, говорит о большей приверженности автора к определенному стилю. В дальнейшем данное исследование планируется продолжить с привлечением других выборок предложений, а также структурных параметров теоретикографовых моделей.

* Работа выполнена при поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.