Теоретико-игровая модель принятия решений по управлению рисками информационной безопасности

П роцесс противоборства между лицом, принимающим решения по управлению рисками информационной безопасности [1] (игрок 1), и нарушителем информационной безопасности (игрок 2) представлен в виде теоретикоигровой модели [5].

Полагаем, что есть непустые, конечные множества F = {f1,…fN} и A = {a1,…,am}, где A – множество путей нападения [3], а F – множество мер безопасности [4, 9]. Игрок 1 выбирает один из элементов f ⊂ F. Для нападения игрок 2 выбирает путь ai ⊂ A. У каждого пути ai ⊂ A есть стоимость нападения q(ai) ∈   Очевидно, что множества F и A можно рассматри вать как множества стратегий игроков 1 и 2 соответственно. Дополним это множество A стратегией «Не нападать», которую обозначим a0. Выбор этой стратегии сводится к нулевой потере для защитника и нулевой выгоде для нападающего. Всякий раз, когда в игре используется путь нападения a и игрок 1 выбирает меру защиты f, он несет рисковую потерю hf,a. Следовательно, когда игроками выбрана пара стратегий (f, a), потеря первого игрока – hf,a, и чистая выгода [7] второго равна hf,a – q(a).

Этот сценарий может быть смоделирован как биматричная игра с двумя игроками, где защитник и нападающий выби- рают свои чистые стратегии f и a в непустых и конечных множествах F и A соответственно (с |A| = m и |F| = N). Для игроков матрицами выплат будут

H = [ h 1 0 ] и Q = [ QI0 ] , (1)

где H и Q – матрицы размера N×m ; (H,[H] _f,a = h_f,a ) – неотрицательная матрица без нулевых строк (нулевая строка подразумевает отсутствие рисков для защитника и может быть исключена), и нет столбца в матрице Q, который доминирует над всеми другими столбцами (наличие такого столбца означало бы однозначный выбор нападающего).

	' q (a a , )	q ( a 2 ) •	• q ( a m Г
	q( ai )	q( a 2 ) •	• q(a m )
Q = H -				.                               (2)
	v q(a , )	q( a 2 ) •	• q ( a m ) ,

«Последний» нулевой столбец в определении H и Q отражает нулевую потерю для защитника и нулевую выгоду для нападающего в случае, если последний выбирает «Не напа-

дать». Далее для простоты будем обозначать эти матрицы H и Q.

Рассмотрим смешанные стратегии этой игры. Стратегией для защитника будет вероятностное распределение g:= (g_f, f ∈ F) на F , и для нападающего вероятностное распределение (u(a), a ∈ a ∪ { a ₀}) на a ∪ { a ₀} . Цель защитника состоит в том, чтобы минимизировать ожидаемую потерю

L (g, u) = E g f I Eu (a) hf, a I ’ f e F    у a e A/ в то время как нападающий пытается максимизировать ожидаемую выгоду

R ( g, u ) = Iu (a) I E gfhf,a - q(a) I • ae A      \ fe F/

Для простоты вектор-столбец из одних единиц длины |F| = N будем обозначать 1 _F , а аналогичный вектор-столбец длины | A| = m как 1 _A . Кроме того, запись e ∈ P, где P – матрица, будет означать, что e принадлежит множеству строк матрицы P.

Многогранник S _H, соответствующий матрице H, в [2] определен как векторная сумма выпуклой оболочки ее строк conv(h₁,…,h_N) и неотрицательного ортанта .

S_H = conv (A,,..., h_N ) + R™.

Строка h_i матрицы H называется несущественной, если она доминирует над выпуклой комбинацией других строк H, иначе говорим, что h_i – существенная. Если все строки H существенные, то матрица H называется надлежащей. Множество существенных строк однозначно соответствует множеству экстремальных точек многогранника S _H. Так как несущественные строки не важны для определения многогранника S _H, то можно исключить их из матрицы H и считать H надлежащей.

В работе [2] введено следующее определение.

Определение 1. Блокатором Ф (S _H ) многогранника S _H называется многогранник

Максимизироват ь 1TF x при условии HTx≤bux≥0,

где H – неотрицательная матрица и b – заданный неотрицательный вектор.

Лемма 1. Значение проблемы линейного программирования вида (10) больше 1, если и только если b принадлежит многограннику S _H, заданному матрицей H.

Доказательство:

Во-первых, заметим, что условие Слатера (достаточное условие сильной дуальности, т.е. эквивалентности решений основной и дуальной проблем выпуклой оптимизации) [6] удовлетворяется для положительного e . Тогда дуальная к (10) проблема формулируется в следующем виде:

Максимизироват ьbTy при условии Hy 1F и y 0.

Ограничения дуальной проблемы (11) задают множество точек равное многограннику Ф (S _H ) (см. (7)). Теперь, если b принадлежит многограннику S _H, то для всех y ∈ Ф (S H ) выполняется b^Ty ≥ 1 (см. (8)).

Наоборот, если b^Ty ≥ 1 для любого y ∈ Ф (S _H ) , то b должна быть в Ф ( Ф (S _H )) (это легко проверить применением Утверждения 1 для многогранника Ф (S _H ) и его блокатора Ф ( Ф (S _H )) ), кроме того, Ф ( Ф (S _H )) = S _H согласно Утверждению 1, следовательно, b ∈ S H .

Поэтому значение дуальной проблемы больше 1. Теперь из-за сильной дуальности получаем, что значение основной проблемы также не меньше 1.

Далее Лемма 1 будет неоднократно использоваться для обоснования существования вероятностного распределения определенного вида, которое может быть получено путем нормализации решения проблемы линейного программирования вида (10).

Пусть SH – многогранник, соответствующий H, а Ф(SH) – его блокатор. Из Утверждения 1 Ф(SH) – многогранник, соответствующий неотрицательной матрице P, строки которой – вершины Из [2] известно, что Ф(SH) – векторная сумма выпуклой оболочки строк P с положительным ортантом. SH – его блокатор согласно Утверждению 1, и где yTx – скалярное произведение y и x.

Взаимосвязь многогранников и их блокаторов устанавливает следующее утверждение.

Утверждение 1. (Фалкерсон, 1971) Если матрица H – надлежащая и многогранник S _H определен выражением (5) , и e₁,…,e_K – экстремальные точки блокатора Ф (S _H ) , а P – матрица, имеющая эти точки в качестве строк, то

5H ={xeR"'|Px>lF}.

Теперь, для строки e матрицы P пишем e = (e(a), a ∈ A ), и пусть Отметим, что т.к. e(a) ≥ 0 для всех a ∈ A и e(A) > 0 , то

( e ( a ) e^S ’

a e A

распределение вероятностей на A , которое будем называть

• 2.    Матрица P – надлежащая, и

• 3.    Ф ( Ф ( 5 H ) ) = S H .

{.xgR"'|P.x>1a.}.

распределением e .

Также определим, для каждого e ∈ P.

h (e) :=

min f e F

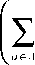
e (a) e (A)

A, ^f , a

Применим это утверждение для решения следующей проблемы линейного программирования [8]:

v ( e ) : = h ( e ) - ^ ^^ q ( a ) , a e A e ⁽ A )

где h(e) – минимальная потеря защитника, если нападаю- щий выбрал цель согласно распределению

( e ( a )

4 A ’

a e A

ν(e) может рассматриваться как ожидаемая выгода нападения в соответствии с распределением e . В самом деле, если нападавший должен был выбрать путь для нападения согласно распределению

( e ( a ) e ⁽ A )’

a e A

то первое слагаемое выражения (14) будет потерей защит- ника, которую мы рассматриваем, как выигрыш нападающего. Второе слагаемое – средняя стоимость нападения,

Если все q(a) = 0, то каждая пара равновесия Нэша соответствует этому пункту.

Отметим, что ν = 0 – особый случай, которому могут соответствовать оба пункта «A» и «B». В обеих ситуациях максимальная достижимая награда нападения равна 0. Существует равновесие, при котором нападающий выбирает стратегию «Не нападать». Защитник должен выбрать g согласно (16). Также может существовать равновесие, при котором нападающий начинает атаку, но получает нулевую ожидаемую выгоду. При таком равновесии стратегия g должна удовлетворять соотношениям (18).

соответствующего распределению e .

Будем называть вершину e многогранника критической, если

v ( ^e ) = max v ( e ) . e e P

То есть соответствующее критической вершине распределение вероятности дает максимум выгоды нападающему (в соответствии с оптимальным выбором защитника).

Определим ν := ν(e) , где e – критическая вершина, и пусть P _max обозначает матрицу, имеющую критические вершины Ф (S H ) в качестве строк. Используем ν в качестве оценки уязвимости с точки зрения защитника.

Пусть (z_e, e ∈ P _max) – дискретное вероятностное распределение на P _max , где все z_e ≥ 0 и

2 ^ . =i .

e max

Теорема 1. Для рассматриваемой игры всегда выполняется следующее:

A. Если ν ≤ 0, то стратегия «Не нападать» (то есть u(a₀) = 1) является оптимальной стратегией нападающего и находится в равновесии Нэша со стратегией защитника (g_f, f ∈ F), удовлетворяющей неравенствам

1. Стратегия «Не нападать»

Покажем, что если ν ≤ 0 , то «Не нападать» и стратегия защитника g , удовлетворяющая (16), являются лучшими ответами друг другу.

Заметим, что если нападающий не выберет стратегию «Нападение», то любая стратегия g приведет к минимальной потере для защитника (0). Теперь предположим, что g удовлетворяет (16). Тогда, a₀ = «Не нападать» является доминирующей стратегией нападающего. Фактически ожидаемая выгода нападения:

R ( g , u ) = Ц и ( a ) (h f ( a ) - q ( a ) )’                       (20)

a e A

которая меньше 0 для любого u , если h g ( a ) - q ( a ) < 0 u V a e A . С другой стороны, нулевая выгода может всегда быть до-

стигнута выбором a₀ . Как следствие, стратегия «Не нападать» – лучший ответ на g , удовлетворяющей (16).

Теперь докажем существование распределения g , которое удовлетворяет (16) при ν ≤ 0 . Ищем g в соответствии со сле-

hg ( a) := У g f hf, a - q ( a) : ^ а e A• f e F

Соответствующие выплаты (3), (4) нулевые.

B. Если ν ≥ 0, то для каждого распределения вероятности (z_e, e ∈ P _max) стратегия нападающего(u(a), a ∈ A), определенная как

( \_ X ^{e (} a )

u ⁽ a ⁾" 5 z " e ( A ) ' e ^c maxx

дующей системой ограничений:

- g> 0,

- I f g 1

^- H ^Tg <  q.

Лемма 2. ν ≤ 0 ⇒ q ∈ S _H.

Доказательство:

Если v ≤ 0 , то для всех e ∈ P

e (a) / \ Г V4 e (a) 7 / f q f a) =^ min f : f h: „ ^h*Ae (A y() meF^Ae (A) f, a J

Или, эквивалентно

находится в равновесии Нэша с любой стратегией (g_f, f ∈ F) защитника, которая удовлетворяет следующим условиям:

q T^e - mi? I ^ e ( a ) ^hf ■ a ^f ’ ^{e f p} f ^e V a ^e A           )

Так как e ∈ Ф (S H ) , то

h g ( a ) — q ( a ) = v для всех a e A npu u ( a ) >  0 h g ( a ) — q ( a ) <  v для всех a e A.

Более того, существует, по крайней мере, одна такая стратегия (g_f, f ∈ F).

Соответствующие выплаты: ν – для нападавшего, и r(z) –

У e ( a ) ^h f , a ^ f 1,                                            (24)

a e A откуда qTe ≥ 1, ∀e ∈ P, следовательно, q ∈ SH.

Используя Лемму 1, мы приходим к заключению, что значение следующей проблемы линейного программирования больше 1.

для защитника, где r (z) := T z f h (e) • e~! max

Максимизировать 1 ^T_Fx

при условии

H ^Tx ≤ qux ≥ 0.

Получим g , удовлетворяющую (16), нормализуя любое решение этой проблемы.

2. Стратегия «Всегда нападать»

Как в предыдущем разделе, сначала докажем, что стратегии, удовлетворяющие условиям Теоремы 1, являются лучшими ответами друг другу. Затем покажем существование распределения (g_f, f ∈ F) , которое удовлетворяет (18).

Лемма 3. Если ν > 0, то стратегия «Не нападать» является строго доминируемой стратегией нападающего.

Доказательство:

Предположим, что e ∈ P _max является критической вершиной Ф (S H ) , и пусть

и e ∈ P _max , потому что для любого такого u подстановкой в (26) получим

R ( g , u ) ^ v .

Как следствие, любое распределение

I e ( a ) u =

I e ( A )

, a e A

Покажем, что нападающий может достигнуть положительной выгоды выбором u (независимо от g ).

При выборе стратегии u ожидаемой выгодой нападающего для любой стратегии защиты g будет

I e ( a )           л I

, a g A

I e ( A )         )

для e ∈ P _max является лучшим ответом, и любая выпуклая комбинация этих распределений – также лучший ответ.

Теперь предположим, что u удовлетворяет (17) для некоторого распределения (z_e, e ∈ P _max) . Тогда распределение (g_f, f ∈ F) , удовлетворяющее (18), соответствует потере r ⁽ z ) = У z e h ( e ) .

e ⁶ P max

Это минимальная возможная потеря для игрока 1 , что видно из следующего соотношения:

R ( g’ u ^У eTa) | L gfhf, a - q (a )|= aeAe ( A )\feF

V ^f V e ^{( a} ) i V e ^{( a} )

= L gf I L     hf. a -У     q (a) ^

feF \ aeAe ( A )       aeAe ( A )

^ L gff h(e )-L e/a) q(a )!= L gfv=v ■ f e F \        a e A e (A)      J f e F

Таким образом,

R (g, u) = v > 0.

(_(

= S g f У I У ^{f e} F    ^ a ^e A ^ e^e Pm-

^ S g f _ f e F

v

max

z -^s I h . ^{e (} A ) J

_ f , a

e (a ¹       I

-(-) hfa ^ e (A) "))

Нижняя граница r(z) может быть достигнута выбором g таким образом, что

Отметим, если ν ≥ 0 , все шаги доказательства сохраняются. Однако стратегия «Не нападать» будет только слабо доминируемой, и, как замечено в предыдущем случае, будет существовать равновесие, для которого нападающий решит не начинать атаку. Другими словами, если ν = 0 , то существует равновесие, для которого u _a = 1 , так же, как равновесие, для которого u _a = 0 .

Как следствие этой леммы мы приходим к заключению, что если ν > 0 , то нападающий никогда не выберет «Не нападать».

Учитывая множество критических строк матрицы Р _max и распределение g , удовлетворяющее (18), любое распределение u вида

u(a)= ^ze для некоторого распределения z = (ze, e ∈ Pmax) позволяет получить выгоду ν. Это максимальная возможная выгода, которую может получить нападающий. Для любого u aeA a eA

У g f ^h f , a = v + q ^{( a} ) f e F

для каждого a ∈ A при u(a) > 0 (существование такого g показано далее).

Это можно увидеть, переписав L(g,u) как

^(^,»)=Ум(а) 'Lgfh aeA

и с помощью простых преобразований

—

r

(z)+r (z)

= v + У z I "Ta eq — h (e)|+r(z) = I e (A) J e e 1 max

= v + У z e ( — v ) + r ( z ) = v — v + r ( z ) = r ( z ) .

e ^e P max

Таким образом, для множества критических вершин P _max распределения, описанные в Теореме 1, являются лучшими ответами друг другу. Как следствие, они формируют равновесие Нэша в случае существования g .

Верхняя граница ν достигается любым

e(«) л(^)’

Теорема 2. Предположим, что ν ≥ 0 и пусть P _max – множество критических вершин. Пусть x* – решение следующей задачи линейного программирования:

Максимизировать 1TFx п р и у с л о в и и        H T x ≤ b u x ≥ 0.

где b = v(A)1A + q. Тогда

• a)    1T. x * = 1,

F

• b)    (HT x*)(a) = b(a), Va e A при u(a) > 0.(35)

равно 1; следовательно, любое решение x* является распределением вероятности на F .

B. Заметим, что

u ^T H ^T x * = r ( z ) 1 _F x * = r ( z ) .                              (41)

Как следствие, x* удовлетворяет (18) и подразумевает существование g .

Доказательство

A. Для доказательства 1 F x * < 1 рассмотрим следующее:

Также H^Tx * <  v 1 A + q из ограничений проблемы (33) линейного программирования, указанной выше. Теперь предположим, что ( H^T x* ) ( a ) < v + q ( a ) для некоторого a е A при u(a) > 0. Тогда

T T * u T H T x

f e F

(

= 2 x * f e F

V a ^e

(

V e ^e Pm.

V Z e ⁽ a ) - ee ( A ) max

A

^ , a

e a ea e (A)

A A

f, a

F x * .

С другой стороны, из ограничения H^Tx* ≤ b , где b = ν(A)1A + q , и из (32) имеем:

u^TH^Tx * <  u^T ( v 1 A + q ) = v + u T q = r ( z ) .                (37)

Комбинируя (36) и (32), получим

r ( z ) T x * <  u ^T H ^T x * <  r ( z ).

Таким образом, 1 ^T _F x * 5 1, для всех допустимых x* , то есть значение задачи линейного программирования (33) не больше 1. Покажем, что b принадлежит многограннику S _H. Для этого докажем, что b^Te ≥ 1 для всех e ∈ P. Действительно,

e^Tb = ve T L + e^Tq = e ( A ) v + e T q >

A              I     e ( A )     J

—Ta ^e T q ⁺ "Ta e T q ^{e ( A} )       ^{e ( A} )

= e(A)h(e ) = e(A )min| У e ⁽ a ) h ^{()()   ()} f ^{e F} I “ ^ e ( A

= min    e (a) h    > 1, m e f I        ( ) f, a .      ’ a eA

f, a

что следует из факта, что e ∈ Ф (S _H ) . Если e ∈ Ф (S _H ) , то по определению блокирующего многогранника

5>(a)If, a > 1 * V/ g F a∈A

Тогда P b ≥ 1 , откуда следует, что b принадлежит блокатору блокатора Ф ( Ф (S _H )) , который эквивалентен S _H.

Теперь, используя Лемму 1, мы приходим к заключению, что значение проблемы больше 1. Это вместе с выводом из неравенства (38) подразумевает, что значение проблемы

uTHTx* = ^u(a)(HTx*)(a) < a e A

< 5* u ( a ) ( v + q ( a ) ) = a e A

= v +5 u ( a ) q ( a) = r ( z ), a e A

где первое равенство доказывается аналогично доказательству (32). Неравенство (42) противоречит выражению (41). Как следствие, H T x * ( a ) = v + q ( a ) для всех a е A при u(a) > 0 . На этом завершается доказательство существования g , удовлетворяющего (18), для любого u вида (17).

3. Случай игры с нулевой суммой

В этом разделе мы рассматриваем игру с нулевой суммой, где все q(a) = 0 . Мы покажем, что для любой пары стратегий защиты (g_f, f ∈ F) и нападения (u(a), a ∈ A) , которые находятся в равновесии Нэша, должно выполняться равенство:

^u ( a ) = Z ^z *

^‘ max

e ( a ) ^{e (} A )

для некоторого распределения вероятности (z_e, e ∈ P _max) .

Как следствие этого, придем к заключению, что стратегия равновесия Нэша g должна быть в форме, данной в Теореме 1. Прежде всего, заметим, что если все q(a) = 0 , то h(e) = ν(e) . Затем, используя структуру игры с нулевой суммой, заме-

чаем, что

v = max

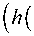
max e e P

(   (_ min f e F I ^

^     у a e A

e(a), e (A) h*,

A

Таким образом, для любой пары равновесия Нэша (g, u) вы-

полняется

v = ZE g T ( a ) hf. = I L g *

f e Fa e A                 f e F

I u ( a ) f , . a e A

> 0.

Из предыдущего неравенства мы можем утверждать, что существует коэффициент масштабирования k > 0 – такой, что ( ku ( a ), a e A ) принадлежит блокатору Ф (S H ) , или аналогично

X ku ( a ) h *. a >  1 * V / e F .

a e A

Пусть g max – максимум g f , и

Ng k = —----, тогда (ku(a), a e A) удовлетворяет (46).

Пусть k обозначает наименьший такой коэффициент из всех возможных k > 0 .

Также отметим, что k – наименьший неотрицательный коэффициент масштабирования (u(a), a ∈ A) – такой, что

(ku(a), a ∈ A) принадлежит Ф (S _H ) , следовательно, здесь должно существовать такое f₀ ∈ F , для которого

X^z - e ( A ) h ( e ) ^X ea * ^{XZ e} h ( e ) ■               (51)

У ku ⁽ a ) f , _a = 1

a e A

Это так, потому что для ∀ ku ∈ Ф (S _H ) и ∀ f ∈ F имеем

У , ku (a ) h f , a ^ ¹ .

a ∈ A

Если бы это неравенство было строгим для всех f ∈ F , то рассмотрение стратегии f_min , которая минимизирует сумму

У ku ⁽ a ) h f, _a , позволило бы построить, a ∈ A

~ k =

k

У u (a)f a e A

Теперь, т.к. v = max (h (e)) , делаем вывод, что ze может быть отличным от нуля только для строки e ∈ P, которая удовлетворяет соотношению h (e) = max (h (e)) . Другими словами, ze > 0 только для e ∈ Pmax. Откуда u ( a) = У P max

e ( a ) ^{e (} A )

Для завершения доказательства Теоремы 1 покажем, что если стратегии (g_f, f ∈ F) и (u(a), a ∈ A) находятся в равновесии Нэша, и (u(a), a ∈ A) имеет вид (17), то (g_f, f ∈ F) должна иметь вид (18). При (u(a), a ∈ A) вида (16) для каждой стратегии (g_f, f ∈ F) выполняется

(_(_  e(a)

У gf Уu ( a ) f =У g f y| У ^ТТ/Л, a= fe F ae A              fe F \ ae A V ee Pmax e(A)

где k удовлетворяет k < k и ku принадлежит Ф (S _H ) . Это противоречит выбору k как наименьшему k .

Теперь рассмотрим следующую лемму.

Лемма 4. Если стратегии (g_f, f ∈ F) и (u(a), a ∈ A) формируют равновесие Нэша игры, то можно написать

= У g f ⁽ У z . | y e S h f , . 11 i y g f ⁽ У z . - 1= v . ^{f e} F   V e ^e P -ax  ^V a ^e A e ⁽ A )      ^{JJ    f e F}   V e^e P max    ^J

ku ( a) = У z e e P

e ( a ) e ( A ) h ( e )

Минимальное значение ν может быть достигнуто выбором g — такого, что У g f h , , a = v для всех u(a) > 0 . Это следует из f^Е f

У , ? / У u ( a ) h f,a = У и ( a ) | У g f h f , a •               (54)

f e F a e A             a G A     у f G F        J

для некоторого распределения вероятности (z_e, e ∈ P _max).

Приведем доказательство этой леммы позже.

Используя выражение (48) для ku(a) покажем, что

Существование такой стратегии g показано в предыдущем разделе. Также было показано, что такая g – лучший ответ на стратегию (u(a), a ∈ A) . Для того чтобы u была лучшим от-

1_ (_ A 1_ (_(_ e A

= — Vg, Vku(a)h,  = — Vg, У Уz, h, v Z-igf \Z-i a ) f,a т Z^gf Z-i Z-i e А к \ f, kf g F   V a g A          ) k f g F V a g A V e g P e (A) h (e))

= 1 X g f ⁽X z ^k f g F   V e g P

1 e (a)              11

i h W X   h f , 'f X^ .

ветом на g , стратегия g должна удовлетворять неравенству:

∑ g f h f , a ≤ v   ∀ a ∈ A(55)

f ∈ F

Предположим, неравенство (54) не выполняется (то есть существуют некоторые a ∈ A, для которых где для доказательства неравенства в третьей строке использовался факт, что

h (e) < У a G A

e^a) h e ( A ) hf■

для ∀ f ∈ F .

Теперь, т.к. (g, u) – пара стратегий равновесия Нэша, вы-

ражение

У u (a) hf a∈A

У g f ^hf , a >  v .

f e F

Тогда нападающий предпочтет переключиться на игровую стратегию a с вероятностью 1 для получения более высокой выгоды. Это нарушает предположение, что (g_f, f ∈ F) и (u(a), a ∈ A) находятся в равновесии Нэша.

Таким образом, g удовлетворяет (55). Теорема 1 доказана при условии, что верна Лемма 4.

минимально для каждого f ∈ F , для которого g_f > 0 . Кроме

того, это минимальное значение равно ν . Тогда

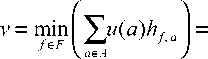
1 • min k f e f

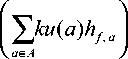
< 1 k ^,

Доказательство Леммы 4

Идея доказательства состоит в том, что, если стратегии (g_f, f ∈ F) и (u(a), a ∈ A) находятся в равновесии Нэша, и k > 0 обозначает наименьший k > 0 , для которого ( ku(a) , a ∈ A ) принадлежит Ф (S _H ) , то должно выполняться равенство:

где используем факт, что минимум меньше выражения

ku (a) = У z e e g P

У ku ( a ) h , , _a — 1 . Следовательно, v = 1/k . a e A

Отсюда, используя (48), получим:

⁽ = k = Nku ( a ) = y y _{Z e}^f a L = ^v      O ^ A ^{V 7} O Z A ^X e ( A ) h ( e )

e ( a ) e ( A ) h ( e )

для некоторого распределения вероятности (z_e, e ∈ P _max) .

Это утверждение требует доказательства, потому что априорно можно написать только

e ( a )

^ku ( a ) = У z e ^f x ^f x + d ( a )                         (57)

e ^ P в ( A ) h ( e )

для некоторого распределения вероятности (z_e, e ∈ P _max) и

некоторого d(a) , a ∈ A , где d(a) ≥ 0 .

Рассмотрим (ku(a), a ∈ A) , для которого

d ( A ) : = ^ d ( a )

име-

У u (a) = a g A

k - d (A) i k - d (A)

a e A ет наименьшее возможное значение. Предположим, что

d(A) > 0 для выражения (57), и докажем формулу (56) от про-

тивного.

Пусть

Для стратегии нападающего (u(a), a ∈ A) в ответ на стратегию защиты (g_f, f ∈ F) выгода нападающего численно не меньше 1/(k – d(A)) . В самом деле,

d h ( f ) ) = У : d ⁽ a ) h f , a , тогда V f e F .

a e A

У g f ^ u ( a ) h^ = feF   aeA

У u (a) hf, a = 1 У ku (a) hf, a = a e A                   a e A

1 Г v-i      - (a)

= * ^ys z - e mo⁺ d ^{( a} ’ J h f ■ - =

= ¹ Y z ^{f 1} У e M hf 1 + ¹ Y d a h_f >  k ^y P ^- ( h ( - )^У - ( A ) f^{, a} J k ^{У (} ) f ’ ^a

(_ = У g f У

f e F

k - d (A )

> k - d(A)

1 у,      e ( a )

V a e A V k - d ⁽ A ) e e P e e ( ^A ) h ( e )

V v ^{1 (}V ^{e ( a} ) ^У g f V ^y z - h ( e ) [ a e A e ( A )

/^F g f '^Уz^- = k - d ( A ) .

f e F

) ) hfa ' 7

У hfA

’)

>

>^-Yz +-d (/) = 1+ dh ⁽ f ) "  k ^Уz^{e +} k h ⁽ f ) k ⁺ k

.

Теперь получаем

min | ^d ⁽ a)^ , _Q |>

^^e V a e A          )

1. .

— + min k f e ^F

d_h ( f ) )

k J

Отметим, что стратегии (g_f, f ∈ F) и (u(a), a ∈ A) находятся в равновесии Нэша, поэтому для всех f ∈ F – таких, что g_f > 0 значение У u ) a ) h f a одинаковое:

a ∈ A

У u ( a ) h f , a = min I y u ⁽ a ) h f , a < - .                  (60)

a e A              f ^e V a e A           } k

Однако для ∀ f ∈ F , при условии g_f > 0 выполняется d(f) = 0 . Следовательно, выгода нападающего в случае использования им стратегии равновесия Нэша (u(a), a ∈ A) равна

<             : : .

k k - d ( A )

Отсюда, если d(A) > 0 , нападающему может быть выгодно изменить стратегию. Это противоречит предположению, что (g, u) формируют равновесие Нэша. Таким образом, из d(A) = 0 следует, что d(a) = 0 для всех a ∈ A , что мы и хотели показать.

Применение результатов

Из (55) и (60) следует, что min У u (a)hf,) = 1 и dh(f) = о feF OZA            k для любого элемента f ∈ F – такого, что gf > 0.

-₌----¹----V „    ^{e (} a )

⁽ ) • k - d ( A ) e b e e ( A ) h ( e ) ’

Тогда

У « ( a ) = 1

a e A

и u ( a ) >  0 для всех a e A .

Отсюда (u(a), a ∈ A) – распределение вероятности на A , которое может быть рассмотрено в качестве стратегии нападающего. Доказать этот факт можно просуммировав (57) по a ∈ A :

k = Yku(a) = y| Yz  (e(aa) ч + dU)| = ui            I e a e A          a e A \ e e P e ( A ) h ( e )         )

= У f l Z e a e A у e e P

e ( a ) e ( A ) h ( e )

= ( k - d (A ))Уй (a) + d (A).

a e A

Из последнего уравнения получаем

На основании рассматриваемой теоретико-игровой модели можно предложить следующий алгоритм принятия решений по управлению рисками ИБ:

• 1)    Формируем множества F и A .

• 2)    Находим h_f , _a ∈ для всех a ∈ A и всех f ∈ F ; а также q(a) ∈      для всех a ∈ A .

• 3)    Для многогранника S _H (формула (5)) строим одну из возможных матриц P по формуле (12).

• 4)    Для всех e ∈ P считаем значения h(e) и ν(e) по формулам (13) и (14).

• 5)    По формуле (15) определяем критические строки матрицы P и вычисляем v как максимально достижимое значение в этой формуле. Формируем P _max как матрицу, состоящую из критических строк матрицы P.

6а) Если ν ≤ 0 , то стратегия «Не нападать» (то есть u(a₀) = 1) – оптимальная стратегия нападающего. Ищем стратегию защитника (g_f, f ∈ F) , находящуюся в равновесии Нэша с указанной стратегией нападающего в соответствии с неравенствами (16). В этом случае потеря защитника и выигрыш нападающего равны нулю.

• 6б)    Если ν ≥ 0 , то для стратегии нападающего (u(a), a ∈ A) , соответствующей выражению (17), ищем стратегию (g_f, f ∈ F) защитника, которая удовлетворяет условиям (18). При этом потеря защитника равна значению выражения (19), а выигрыш нападающего равен v .

Примечание 1: Если q(a) = 0 для всех a ∈ A , то всегда выполняется шаг 6б).

Примечание 2: Распределение (z_e, e ∈ P _max) позволяет описать множество равновесий Нэша игры. Оно может использоваться, например, для моделирования предпочтений нападающего при атаке. В простейшем случае это распределение является распределением равновероятных событий.

• 7)    Смешанная стратегия (g_f, f ∈ F) позволяет осуществлять распределение ресурсов при управлении рисками ИБ: каждая вероятность события g_f отражает пропорцию ресурсов, приходящихся на соответствующий элемент f ∈ F . Смешанная стратегия (u(a), a ∈ A) отражает наиболее вероятные пути нападения на систему защиты игрока 1 ■

  • 1.    ISO/IEC 27005:2011, Information technology – Security techniques – Information security risk management. Geneva, 2011.

  • 2.    D.R. Fulkerson. Blocking and Anti-Blocking Pairs of Polyhedra./ Math. Programming, 1971. – No. 1. – PP. 168 – 194.

  • 3.    BSI: Attack Pattern Glossary. – Cigital Inc., 2006.

  • 4.    NIST IR 7298 Revision 1. – Glossary of Key Information Security Terms, 2011

  • 5.    Данилов В.И. Лекции по теории игр. – М.: Российская экономическая школа, 2002.

  • 6.    S. Boyd and L. Vandenberghe. Convex Optimization. – Cambridge University Press, March 2004.

  • 7.    Гальперин В.М., Игнатьев С. М., Моргунов В.И. Микроэкономика. В 2-х томах. – СПб: Институт «Экономическая школа», 2004.

  • 8.    L.A. Wolsey and G.L. Nemhauser. Integer and Combinatorial Optimization. /1st ed. – Wiley-Interscience, November 1999.

  • 9.    Национальный стандарт Российской Федерации ГОСТ Р 53114-2008. «Защита информации. Обеспечение информационной безопасности в организации. Основные термины и определения».