Теоретико-информационные границы точности кодирования сообщений и распознавания образов по ансамблям данных

В задачах кодирования источников дискретных сообщений с допустимой погрешностью и задачах распознавания образов (классификации) важной характеристикой качества принимаемых решений является вероятность ошибки, которая зависит от количества обрабатываемой информации. Известное в теории информации соотношение между количеством информации и вероятностью ошибки определяется функцией «скорость-погрешность» [1], которая дает наименьшее количество информации при заданной вероятности ошибки либо наименьшую вероятность ошибки при заданном количестве информации. Такое соотношение не зависит от алгоритмов кодирования и является двухфакторным критерием качества кодирования дискретных сообщений с погрешностью, измеряемой в метрике Хемминга. В настоящей работе предлагается обобщение указанного соотношения для кодирования дискретных сообщений, переданных по каналу с шумом.

В теории классификации известны методы оптимизации решающих алгоритмов, которые позволяют минимизировать вероятность ошибки [2, 3]. Однако эти методы ориентированы на конкретные алгоритмы и не дают общего подхода для нахождения потенциально достижимой точности при заданном количестве обрабатываемой информации. Поскольку теоретикоинформационная модель классификации данных схожа с моделью кодирования сообщений, переданных по каналу с шумом, естественно найти соотношение между количеством обрабатываемой информации и потенциально достижимой вероятностью ошибки классификации, которое не зависело бы от алгоритмов принятия решения.

Построение соотношений вероятности ошибки и количества обрабатываемой информации для указанных моделей кодирования и классификации базируется на рассмотренной в [4] схеме кодирования непрерывных сообщений с квадратичной погрешностью. В отличие от традиционной схемы кодирования источника с допустимой погрешностью [1, 5], в такой схеме кодирование выполняется на выходе стохастического канала наблюдения, который вносит неустранимую погрешность.

В работе [6] получены зависимости наименьшего количества обрабатываемой информации от допустимых значений вероятности ошибки для моделей кодирования и классификации, в которых выходы каналов наблюдения представлены данными одной модальности. Цель настоящей работы состоит в построении таких зависимостей для моделей кодирования и классификации с составными каналами наблюдения, выходы которых представлены данными различной модальности. Зависимости наименьшего количества обрабатываемой информации от вероятности ошибки строятся в форме монотонно убывающих функций. Поэтому обращения таких функций дают значения потенциально достижимой вероятности ошибки при различных значениях количества используемой информации. Такие соотношения могут быть полезны для анализа эффективности алгоритмов кодирования и классификации, поскольку позволяют оценить избыточность вероятности ошибки алгоритмов относительно потенциально возможных значений при любом количестве обрабатываемой информации.

Структура работы включает формализацию моделей кодирования и классификации (параграф 1) и построение для рассматриваемых моделей аналитических нижних границ вероятности ошибки при заданном количестве обрабатываемой информации (параграф 2). В параграфе 3 приводятся примеры таких границ для схемы кодирования статистически независимых сообщений с двумя каналами наблюдения и для схемы классификации изображений лиц и подписей по составным объектам «лицо-подпись».

1. Вероятностные модели кодирования и классификации

Модель кодирования дискретных сообщений, переданных по каналу с искажениями

Рассматривается модель кодирования дискретных сообщений с допустимой погрешностью в терминах понятий, принятых в теории информации [1]. Сообщениями источника являются статистически независимые символы алфавита U размера q >  2, на котором задано распределение вероятностей

P u = { P u ( u ) } .

Символы алфавита U передаются по составному каналу наблюдения, выход которого образован ансамблем V M = V 1... V M q -ичных алфавитов V m , m = 1, . , M . Каждому входному символу u e U составного канала соответствуют столбцы выходных векторов v M =( v 1 , . , v m ) ^t , v_m e V m , m = 1, . , M , с условными вероятностями

P V M | U = { ^P V ^M | U ⁽ v I u ) } .

Символы алфавита U воспроизводятся по сообщениям из ансамбля V^M безошибочно либо с погрешностью символами алфавита U = U . На алфавите U вводятся свободные условные распределения

QUVM ={Qu\vM (u| vM )}, которые образуют канал воспроизведения.

Рассмотрим схему кодирования блоков u N =( u 1 ,..., u_N ) символов u n e U , n = 1, . , N , в блоки u^N = ( u 1 ,..., й_N ) символов й_n e U , n = 1, . , N . Каждому u^N соответствует блок v^MN = ( v M ,..., v N ) столбцов v M e V^м , n = 1,..., N , на выходе составного канала наблюдения, и блок u ˆ ^N строится по предъявляемому блоку v^MN . Указанные блоки образуют множества

U N ={ u^N }, V^MN ={ v^MN }и U N = { u N }. При этом независимость символов источника и использование канала наблюдения и канала воспроизведения без памяти порождает на указанных множествах следующие распределения

P j n ( u^N ) = П P u ( u n ) ( - n =1

^P _V MN j N =< P V MN j N ⁽ v^MN । u^N ) = П ^P _V M U ⁽ v^{M 1} u n ) | ’   ⁽²⁾

l                                 n =1

¹U N V MN = \ ^Q U N V MN ( u ^{N 1} v^MN ) = П ^Q U\ _V M ⁽ u n ¹ v^M ) | . ⁽³⁾ l                                  n =1

Множества U^N , V^MN , U^N с распределениями (1) – (3) образуют пару последовательных стохастических преобразований

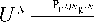
VMN

Q U ˆ ^N V^MN

A

U ^{ˆ N} .

Используя побуквенную меру погрешности Хемминга между любой парой блоков u^N e U N и u^N e U^N , для схемы (4) вводится средняя на символ источника погрешность

E Q UNVMN (V^MN ; U N ) =

= ( 1 N ) £ P v mn ( v^MN ) £ Q u , n V MN ( u ^N I v^MN ) X         (5)

V MN              U ˆ N

N x£PjnVMN (uN|vMN )£ d(un ,Un )

U N                           n =1

и средняя на символ взаимная информация

I Q UNVMN ( V ^MN ; U N ) =

= ( 1 N ) £ P v mn ( v^MN ) X Q u n V MN ( u ^N I v^MN ) X         (6)

V MN              U ˆ N

Q_U ˆ N _{| V} MN ( u ˆ ^N | v^MN )

X In-----------x-------- ,

Q U ˆ N ( u ˆ ^N )

где

d ( u_n , u ˆ _n )

, u n * u n

0, u n = u n'

P y N V MN ( u^N | v^MN ) =

P U N ( u^N ) P V MN | U N ( v^MN | u^N ) P_V MN ( v^MN )

P V MN ( v^MN ) = £ P_U N ( u^N ) P V MN ^ N (v^MN | u^N ),

U ^N

Q u n ( u^N ) = £ P v mn ( v^MN ) Q u n V MN (u^N | v^MN ).

V ^MN

Поскольку в (5) сумма по блокам u^N в пересчете на символ источника дает вероятность ошибки на блоке воспроизведения u ˆ ^N по наблюдаемому блоку v^MN , средняя на символ погрешность вида (5) соответствует вероятности ошибки на множестве блоков воспроизведения U ^{ˆ N} по множеству наблюдаемых блоков V^MN .

Зависимость функционалов (5) и (6) от свободных условных распределений вида (3) позволяет при заданных значениях s > 0 ввести функцию «взаимная информация-вероятность ошибки»

Rmn (s) =     min     IQ^ N   (VMN; UN)(7)

QUˆ N|VMN:

Eo-m (vAvmn;иN)

порядка N , где минимум берется по всевозможным условным распределениям Q и n^ при s -ограничении вероятности ошибки. Учитывая, что распределения вида (1)–(3) заданы в форме произведений, функционалы (5) и (6) эквивалентны значениям E Q _{U ˆ |VM} ( V^M ; U ^ˆ ) и I Q _{U ˆ |VM} ( V ^M ; U ^ˆ ) при N =1. В этом случае функция (7) не зависит от N и может быть представлена в форме

R m ( s ) =     min    I q и ( V^м ; U ).                 (8)

Q U ^ˆ |V ^M :

E Q _и ( V ^м ; •

Задача состоит в получении для функции (8) монотонно убывающей неотрицательной нижней границы R M ( s ) <  R M ( s ). Тогда обратная функция R м ¹( I ) дает нижнюю границу вероятности ошибки кодирования источника при фиксированных значениях средней взаимной информации I .

Модель классификации составных объектов

Рассматриваемая модель классификации аналогична рассмотренной модели кодирования и формулируется в терминах понятий, принятых в теории классификации [7]. Классы представлены множеством меток Q = { ю i , i =1,..., c } Р = { ю , , i = 1,..., c } , c >  2, с априорным распределением вероятностей

P q= { P q CM c_ _r                             (9)

, =1

Классифицируемые составные объекты образуют ансамбль множеств X ^м = X 1 _ X _м , в котором X m , m = 1,..., M - множество объектов, порождаемых m -м источником. Каждый составной объект задан столбцом объектов x ^м = ( x 1 , . , x _м ) t e X ^м одного класса, элементы которого x _m e X _m , m = 1, . , м , являются объектами соответствующих источников. Будем считать, что на ансамбле X ^M заданы условные по классам распределения

P x м р = { P X м р ( x ^м |й0 } c ,,                        (10)

I =1

которые образуют составной канал наблюдения. Решения о классах составных объектов образуют множество оценок Р = { ю j , j = 1,..., c } меток классов.

В общем случае решение принимается по блоку составных объектов одного класса xMN = (xм,...,xм), в котором xм e Xм,n = 1,...,N. Блоки составных объектов образуют множество XMN = {xMN}. Для составного канала наблюдения без памяти условные по классам распределения вероятностей блоков составных объектов с учетом (10) имеют вид

1_I

PX MN Q = | PX MN|Q (x MN 1 Ю) =П PX мр (x м 1 Ю) Г.

I

На множестве оценок классов Q вводятся свободные условные по блокам составных объектов распределения вероятностей

QpxMN ={ Qpx MN (jMN )}.(12)

Множества Q , X ^MN и Q совместно с распределениями (9), (11) и (12) образуют последовательность стохастических преобразований

Q PX'   > XMN   QX' > Q.(13)

Используя меру погрешности Хемминга между истинными классами и их оценками в схеме (13), вводится средняя вероятность ошибки

EqqxMN (XMN; Q) = cc(14)

= Ё Q ⁽^^{| x MN} ) £ P ( ю ^{1 x MN} ) d ⁽ ю , ю )

j=1

и средняя взаимная информация

I q q x MN ( X ^MN ; Q) =

= Ё PxMN (xMN)EQq|xMN (Юj|xMN ) X

Xм

, Q Q| X MN ( j ^MN )

X In----!-----7---x----- , QqW где

Г 1, ю , ^ ю j d ( ю , , ® j ) = ^               ,

[ 0, ю , = ю j

P q | X MN ( ю , | x ^MN ) =

P q ( ю , ) P x MN |Q ( x ^MN | ю , ) P _X MN ( x ^MN )

c

P x MN ( x ^MN ) = Ё P q ( ю , ) P x мN | q ( x ^MN | ю , ), i =1

Q й C Ю j ) = Ё P x MN ( x ^MN ) Q q | x MN ( ю _J\ x ^MN ). x MN e X MN

Зависимость функционалов (14) и (15) от свободных условных распределений (12) позволяет при значениях s >0 ввести соотношение «взаимная информация-вероятность ошибки» в форме условного минимума

R м ^{( s )} = min min I Q_q^ n ^{( X MN} ;^{Q )} . ^{(16) N Q} Q X Ш : ¹

^E q _{q x} MN ( X ^MN ;^Q ■ •

Внутренний минимум в (16) берется по всевозможным распределениям Q^XмN при заданном s-ограничении средней вероятности ошибки, а внеш- ний – по длине блоков N. Для модели классификации, как и для модели кодирования, задача заключается в построении монотонно убывающей неотрицательной нижней границы RM (s) < RM (s). Тогда обратная функция RM(I) дает нижнюю границу вероятности ошибки при заданных значениях средней взаимной информации I.

• 2.    Вычисление функций«взаимная информация-вероятность ошибки»

Нижняя граница функции R m ( s )

Построение нижней границы R_M ( s ) <  R M ( s ) для функции (9) базируется на дискретной модификации подхода, предложенного в работе [4] для вычисления функции «скорость-погрешность» в схеме кодирования непрерывных сообщений, переданных по каналу с шумом. Согласно такому подходу, вводится последовательность преобразований V^м и U * ^ U , где U * = U = U .

Преобразование Vм и U является детерминированным по критерию максимальной апостериорной вероятности u * = arg max P(u | vM). Этот критерий обеспечи-и eU вает наименьшую вероятность ошибки sM ’min и вероятность выхода PU* (и *) = ^ vM eVM PVм (vM) для подмножества V*м с Vм векторов, отображаемых в символ и * e U *. Преобразование U * -и U является стохастическим, в котором переходные вероятности Q^U* (U| и *) совпадают с вероятностями QuVM (и | Vм) для векторов Vм e V*м и дают условные распределения

Q и \ и * = { 0 ; ^ * ( и\и ) } .                                 (17)

где минимум берется по всевозможным условным распределениям (17) при ограничении средней вероятности ошибки преобразования U * U U величиной s - s M ’min >  0 . Тогда нижняя граница функции (20) следует из границы Шеннона для функции «скорость-погрешность» в схеме кодирования U * U U с погрешностью в метрике Хемминга [5]. Полученная граница сформулирована в следующей теореме.

Теорема 1 . Функция R m ( s ’, определенная в (7), имеет монотонно убывающую нижнюю границу

R m ( s ’ = I(U ; V^м ) - h ( s-s M min ) -- ( s-s M min )in( q - 1)

на отрезке s M m in < s < s M max , где I ( U ; V^м ) - средняя взаимная информация между U и V^M , h ( z ) = - z ln z -(1- z ’ln(1- z ), R m ( s M min ) = I(U ; V^м ) и ^R M ^{( s} M max ’ = ⁰ .

Доказательство . Согласно [5] нижняя граница Шеннона для функции R_M ( s ), переопределенной в форме (20), имеет вид

R m (s ) = H ( U * ) - H s ( U \ U * ) ,                   (22)

где

H ( U * ’ = - E P u * ( и * )ln P u * ( и * ) u * e U *

– безусловная энтропия на множестве решений U ^* и

Hs ( U| и ) =

= - E P u * ( и * ’ Z Q UU * ( и \ и * ’ln Q UU * ( и \ й ) и * e U *            UeU

– условная энтропия по распределениям

С учетом неравенства треугольника d ( и , й) <  d ( и , и * ) + d ( и* , й) и распределений (17) средняя вероятность ошибки (5) при значении N = 1 удовлетворяет неравенству

E Q U | _гм ( V^м ; U ) M ’mn+EQ U| U* (U *; и) =

= s M mn + E P u * ( и * ’ E Q uu * ( U | u * ’ d ( и * , и ). и' e U *            UeU

Благодаря детерминированному преобразованию

V M U U * , средняя взаимная информация (6) в случае

N = 1 принимает вид

i q и vm (V ^м ; U ) = I q и и * ( и * ; U ) =

„                            Qrn /*( U | u * )        (19)

= E P u * ( и* ’ E Q uu * ( U | u * )ln ^UU^T- .

и                   ^{|                 q}u⁽ и )

Соотношения (18) и (19) преобразуют функцию (8) к виду

Rm (s) =

min

Q U | U * : E Q _{и | и} * ( ^U * - ^U )M’min

I Q UU *

( U * ; U ),

( s ) U ^ˆ | U

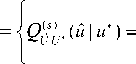
exp ( - sd ( и * , U ) )

E _{U e U} ^exp ( ^{- sd ( U} * , ^{U )} )

с параметром s >0.

Поскольку формула (8) эквивалентна известной функции «скорость-погрешность», которая ограничивает снизу скорость любого кода с заданной погрешностью [1], энтропия выхода детерминированного преобразования V^м U U удовлетворяет неравенству H ( U * ) >  R m ( s M min ). В этом случае R m ( s M m_m ) равно минимальной средней взаимной информации в (8), которая достигается на апостериорных распределениях, обеспечивая R_M ( s M )_min ) = I (U ; V^м ) и оценку

H (и *) > I (и; Vм).

Для нахождения параметра s в распределениях (23) используем равенство

E P u * ( U * ) E Q UU * ( U | U * ) d ( U * , U ) = s - s M min ,

U * e U *            UeU

которое дает e ^{- s} = ( s-s M min )/( q - 1) ( 1 - ( s-s M min ) ) ,

Q UsU . ( U | u * ) =

J 1 - ( s-s M imin ), u = u * 1 ( ^s-s M D/c q — 1), a ^ u *

В случае равновероятных символов алфавита U максимальная вероятность ошибки равна sMmax = (q -1)/q и оценка (27) преобразуется к виду и условную энтропию

H s (U \ U * ) = h ( S - s M m_m ) + ( S - s M min ) ln ( q - 1) . (25)

( q )

M min = q -1Г 2H(U \ Vм)

q I q ^{- 1}

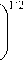
Последующие замены условной и безусловной энтропии в (22) правыми частями соотношений (24) и (25) завершают доказательство теоремы 1.

Граница (21) является обобщением нижней границы Шеннона для функции «скорость-погрешность» в схеме кодирования независимых дискретных сообщений с допустимой средней погрешностью в метрике Хемминга [1]. В границе Шеннона используется бесшумный канал наблюдения, который обеспечивает H ( U | V^M )=0 и I ( U ; V^M ) = H ( U ). При этом R m ( s M m_m ) = H ( U ) и s M m_m = 0 . В общем случае нулевое значение R M ( s M max ) = 0 достигается в точке s M max = ( q - 1)min P ( u ).

Минимальная вероятность ошибки s M min зависит от величины условной энтропии H ( U \ V^м ) >  0. Для нахождения этой зависимости воспользуемся разностью границы Шеннона и границы (21) в точке s = s M max .

Указанная разность дает равенство h (sM max)—h (sM max—sM mn)+smmin ln( q—1)=

= H(U | Vм), которое с учетом разложения в ряд Тейлора

Оценки (27) и (28) демонстрируют уменьшение минимальной вероятности ошибки s M ’min с уменьшением условной энтропии H ( U | V^M ) и, следовательно, с ростом средней взаимной информации I ( U ; V^M )= H ( U )– H ( U | V^M ). Этот эффект проявляется с увеличением числа каналов M . При отсутствии шума в составном канале наблюдения имеем H ( U | V^M )=0 и s M min = 0. В этом случае I ( U ; V^м )= H ( U ) и граница (21) совпадает с границей Шеннона, приведенной в [1].

Иллюстрация множества U и ансамбля V 1 V 2 , а также характер функции R _m ( s ) при значениях M =1 и M >1 (сплошные кривые) показаны на рис. 1. Пунктирная кривая демонстрирует поведение нижней границы Шеннона. Множество U представлено круговой областью, множества V 1 и V 2 – эллиптическими областями. Указанные множества демонстрируют увеличение с ростом M средней взаимной информации I ( U ; V^M ) как теоретико-информационной меры пересечения U ∩ V^M (серая область) и уменьшение условной энтропии H ( U | V^M ) как теоретико-информационной меры разности U \ V^M (темная область), что приводит к уменьшению вероятности ошибки s M min ■

( q )                  ( q )

^,l ( ^S M max )    ( ^S M max

-

( q )

M min

( q )         ( q )

^{( S} M max ^{) S} M min

+ —

( q )

I ^{h ( S} M m

)| ( s m m_m ) ² + о (

( q )

^S M min

при малых значениях s M min принимает вид

1       ( ^q )

2 h ^{( S} M max

+

+ ( h ‘ ( s M mx ) + ln( q - 1) ) s M ) min = H(U | V^м ).

Решение уравнения (26) с производными

)

(q)          1___SM max h (SMmax) = ln   (q)

^S M max

| h "(s M U)|

⁽ q ) ^S M max

(1 -s M max ) )

дает асимптотическую оценку

s M ) min =s M ’mxa -s M mx ) x l ln ² 1 ( q - 1)

( q )

( ^S M max )

( q )

^S M max

+

1/2

₂ —^H(^U | V ’ — ^     ) л__е( « ’

+                     I S M max( S M max)x sM )max(1 -SM ’max) J

x In l ( q - 1)

( q )

( ^S M max )

( q )

^S M max

.

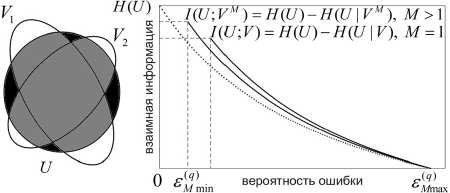
Рис. 1. Интерпретация средней взаимной информации I (U;V^M) и поведение функции Rm ( е )

Необходимо отметить, что в практике кодирования q -ичных сообщений со скоростью R ^{( q )} и вероятностью ошибки E^q ’ граница R _m ( s ) позволяет вычислить избыточность r ( R ^{( q} ’ \ E ^{( 4} ’ ) = R ^{( q} ’ - R _m ( E ⁽ q ’ ) скорости кода относительно потенциально возможного значения при заданной вероятности ошибки. Использование обратной функции от R _m ( s ) дает избыточность

r ( E ⁽ q ’ | R ⁽ q ’ ) =

J e ⁽ q ’ - r _m¹( r ⁽ q ’ ), r ⁽ q ’ <  I(U ; V^м ) [ e ⁽ q ’ -s M ’min , R ⁽ q ’ >  I(U ; V^м )

вероятности ошибки при заданной скорости.

Нижняя граница функции R _m ( s )

Методика построения нижней границы

R _m ( s ) <  R _m ( s ) функции (16) аналогична методике,

использованной для получения границы (21). Пусть « * ={ го k , k =1,..., c } - множество меток классов, получаемых на детерминированном преобразовании X MN ^ q * с наименьшей вероятностью ошибки s M ’_min при длине блоков N * > 1. Такое преобразование реализуется на решающем правиле по максимуму апостериорной вероятности классов и порождает разбиение множества X ^{MN *} на непересекающиеся подмножества X ^MN ' ^го _k , k =1, . , c , с вероятностями P (го k ) = ^ x MN '_{e X} N ' P ( x MN ' ), k =1,..., c . В этом случае условные по блокам x ^MN ' е X ^N ' вероятности Q _{Q | X} у ' ( ^M j I x MN ' ) = Q q_Q' ( ^ю / I го k ) дают условные распределения

Q q | q' = { Q q i q ' ( го , I го k ) } .

С учетом неравенства треугольника d ( го i , го j ) <  d ( го i , го k ) + d ( го k , го j ) и распределений (29) средняя вероятность ошибки (14) удовлетворяет неравенству

E%MN' (XMN' , Q)     ’min + EРф. (Q‘ , Q’ = c c                                 (30)

= ^s M min ⁺ ^ ^P Q ' ^{( го} k ) X Q (!|Q ’ ^{( го} j ^{1 го} k ’ ^{d ( го} k , ^го j ).

При этом средняя взаимная информация (15) принимает вид

I «,, ■ ( X ”' ;^Q) = I «., (^ff;^Q) =

Q q_Q' ( го j | го _k )      ⁽³¹ ’

= Z P Q ' ^{( го} k ’ Z Q Q | Q ' ( “ j ^{1 го} k ^)ln   ' , , --- .

t!        j 1                  ^Q « ( го )

Доказательство. Аналогично доказательству теоремы 1. Для функции R _m ( s ) в форме (32) применима нижняя граница [5]

Rm (s) = H (Q') - Hs (QIQ') ,                  (34)

где

c

H (Q*) = -Z Pq' (го k ’ln Pq' (го k)

k =1

- безусловная энтропия на множестве решений Q * и

Hs (Q| Q') = cc

= - Z P q' ( го k ) Z Q QQ ' ( ГО j I го k )ln Q QQ ' (ГО j I го k ) k =1               j =1

- условная энтропия по распределениям

^Q          Q Q S Q ' ( гo j | гo k ) =

= exp ( - sd ( го k , Гo j ) )

Z c = i ^exP ( ^{- sd ( го} k , го’ )

с параметром s >0.

Согласно теореме кодирования [1], энтропия выхода преобразования X ^mN ^Q * удовлетворяет неравенству H ( Q * ) >  I ( Q ; X ^MN ). Кроме того, при любой конечной длине блоков N для ансамбля X ^MN = X ^м ... X ^M справедливо неравенство I (Q; X ^MN ) >  I (Q; X M ) , которое в случае тождественных множеств X M = X ^м , n = 1, . , N , выполняется со знаком равенства [1]. Тогда I ( Q ; X ^MN* ) = I ( Q ; X ^M ) и

H (Q') > I (Q; XMN') = I (Q; Xм).               (36)

Соотношения (30) и (31) преобразуют функцию (17) при значении N = N * к виду

Для нахождения параметра s в распределениях (35) воспользуемся равенством

Rm (s) =

min

!Q | Q' ^: E Q _Qq («' «        ■ ’min

iqq« («'; Q),

cc

Z P Q ' ^{( го} k ’ Z Q Q s Q ' ( го ^{1 го} k ’ ^{d ( го} k , ^гo j ’ = ^{s - s}» , k =1               j =1

где минимум берется по всевозможным условным распределениям (29) при условии, что второй член в правой части (30) не превосходит величины s-s M ’_min >  0. Тогда нижняя граница функции (32) следует из нижней границы Шеннона для функции «скорость-погрешность» в схеме кодирования Q ' ^ Q с погрешностью в метрике Хемминга, когда средняя погрешность не превосходит s - s M ’_min [5].

Теорема 2 . Функция R_M ( s ), определенная в (16), имеет монотонно убывающую нижнюю границу

R m ( s ) = I ( Q ; X ^M ) - h ( s-s M ’min ) - ( s-s M кЖ c - 1) (33) на отрезке s M ’_mm M ’_max , где I ( Q ; X ^M ) - средняя взаимная информация между множествами Q и X M , h ( z )=- z ln z -(1- z )ln(1- z ), R m ( s M ГО) = I ( Q ; X ^M ) и R M ( s M ’max ) = 0.

откуда следует e ^{- s} = ^{( s-s} M ’min ’/⁽ c ^{- 1)} ( 1 ^{- ( s-s} M ’min ’ ) ,

Q Q s Q ' ( го _у -| го k ) =

1 - (s-sM’min’, j = k, (s-sM’min)/(c - 1), j * k, и условная энтропия

H s (QIQ ' ) = h (s - s M ’min ) + (s - s M ’min ) ln( c - 1) . (37)

Последующие замены условной и безусловной энтропии в (34) правыми частями соотношений (36) и (37) завершают доказательство теоремы 2.

В общем случае область определения границы (33) задается минимальной sM’min > 0 и максималь ной sM’max = (c- 1)minP(го,-) вероятностями ошибки. i=1

При этом, как и в схеме кодирования (4), минимальная вероятность ошибки в схеме классификации (13)

должна уменьшаться с ростом средней взаимной информации между входом и выходом канала наблюдения. Для демонстрации этого эффекта полезно привести асимптотические оценки минимальной вероятности ошибки.

Применяя технику, аналогичную используемой для вычисления асимптотики минимальной вероятности ошибки в модели кодирования, для малых значений e M m, получаем асимптотическую оценку

( c ) M min

_ _с ( С )            ( С )              2 I ^{(1 £} M max ) | ,

-£Mmax(1 eMmax) Xl ln I (c 1)    (c)

\ \         e M max

H ( Q | X ^M )

1/2

+ 2

(c)( e M max(   e M max)

-e MM UI-e M Lj ln l ( c - 1)

^{(1 - e} M max

)

( c )

^e M max

которая при равновероятных классах принимает вид

( c )

M min c -1 ( 2 H (Q | XM) c ^ c -1

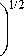
Оценки (38) и (39) демонстрируют уменьшение минимальной вероятности ошибки e M mn с уменьшением условной энтропии H ( Q \ X ^M ) и, следовательно, с увеличением средней взаимной информации I ( Q ; X ^M )= H ( Q )- H ( Q \ X ^M ). Уменьшение энтропии H ( Q | X ^M ) и, соответственно, минимальной вероятности ошибки e M mn может быть достигнуто путем увеличения числа M источников в ансамбле.

При нулевом значении условной энтропии H ( Q | X M ) = 0, которое дает наибольшую среднюю взаимную информацию I ( Q ; X ^M )= H ( Q ), граница (33) совпадает с нижней границей Шеннона для функции «скорость-погрешность» в схеме кодирования независимых дискретных сообщений с допустимой средней погрешностью в метрике Хемминга [1]. В этом случае e M m, - 0 и R m ( e M mn ) - H ( Q ). Следует отметить, что граница Шеннона соответствует модели классификации, в которой каждый объект априори принадлежит одному классу [8]. Формально это означает, что апостериорные вероятности классов по каждому объекту (простому или составному) принимают значения 1 или 0, обеспечивая H ( Q | X ^M ) = 0.

Рис. 2 иллюстрирует множество классов Q , ансамбль X 1 X 2 и поведение функции R_M ( e ) при M =1 и M >1 (сплошные кривые) и границы Шеннона (пунктирная кривая). Множество Q представлено круговой областью, множества X 1 и X 2 – эллиптическими областями. Из рисунка следует, что с увеличением M средняя взаимная информация I ( Q ; X ^M ) увеличивается как мера пересечения Q A X ^M (серая область), а условная энтропия H ( Q | X ^M ) уменьшается как мера разности Q \ X ^M (темная область), что приводит к уменьшению минимальной вероятности ошибки e M m_in ■

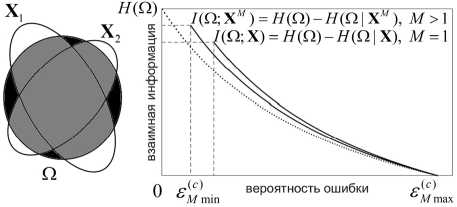
Рис. 2. Интерпретация средней взаимной информации

I (Д' X ^м) и поведение функции R_M ( e )

Практическая значимость границы R_M ( e ) состоит в возможности использования обратной функции для вычисления избыточности

_ _ Г E ^{( c} ) - R -1 ( H ^{( c} ) ) , H ^{( c} ) <  I ( Q ; X ^м ), r ( E ^{( c} ) | H ^{( c} ) ) -^         ^{м (} ) ,           ^{( ;} ),

[E(c) -eMU , H(c) > I(Q;XM), вероятности ошибки E(c) любого решающего алгоритма относительно потенциально возможного значения при заданной энтропии H(c) решений о классах предъявляемых объектов. Избыточность r (E(c)|H(c)) может быть вычислена для классификаторов с различными разделяющими функциями и, в частности, для многоклассовых SVM классификаторов с разделяющими функциями сигмоидного типа [9]. Кроме того, теоретико-информационный критерий минимизации вероятности ошибки при фиксированных значениях средней взаимной информации между обучающим множеством данных и множеством решений об их классах может найти применение в процедурах оптимизации отбора признаков [10] и, в частности, при обучении нейронных сетей [11].

• 3.    Примеры нижних границ

Схема кодирования независимых равновероятных сообщений с двумя каналами наблюдения

Рассмотрим вычисление границы R_M ( e ) вида (21) для схемы, в которой составной канал наблюдения задан M >1 независимыми каналами. Значение M =1 соответствует схеме с одиночным каналом наблюдения. Множества переходных вероятностей P V m | U , m =1,..., M , таких каналов порождают на ансамбле V^M множество условных распределений

Г

PVM U — 1 PVMU (v 1 u) -П PVm U (vm 1 u )[■

I

С учетом распределений (40) средняя взаимная информация I (U; V^M ) в (21) согласно [1] выражается через соответствующие энтропии в форме

M

I ( U ; V^м ) - H (V^м ) - £ H (V m \U ),            (41)

m -1

где

H(V^м ) - - £ P v m ( v^M ) In P v m ( v^M ),

V ^M

H (V m | U) = - X P u ( u ) £ P U ( V m I u ) In P v m U ( V m । U ), UV m

P v m ( V^M ) = X P u ( U ) P v m U ( V^M Iu ).

U

В случае M =1 формула (41) дает значение средней взаимной информации между входом и выходом одиночного канала наблюдения.

В приведенном ниже примере используется алфавит источника U размера q >  2 с одинаковыми вероятностями P U ( u ) =1/ q и составной канал наблюдения, который содержит M =2 симметричных канала с выходными алфавитами V m = U , m =1,2. При вероятности 0< 3 _m <1 ошибочной передачи символа источника такие каналы имеют условные вероятности выходов

^P V m | U ⁽ v m ^{1 U} ) =

1 -3 m , V m = U , 3 m /( q — 1), V m * U .

Вычисление энтропий в (41) при значении M =2 дает среднюю взаимную информацию

I(U ; V v 2 ) = ln q - h ( 3 1 ) -3 ! ln( q - 1) +

+ h ( 3 1 +3 ₂ -3 1 3 2 q /( q - 1) ) -                      (42)

- h ( 3 2 ) + ( 3 1 -3 1 3 2 q /( q - 1) ) ln( q - 1) .

Правая часть в (42) представлена суммой средней взаимной информации

I(U ; V ) = ln q - h ( 3 1 ) -3 1 ln( q - 1)

и условной средней взаимной информации

I(U ; V 2 1 V 1 ) = h ( 3 1 +3 2 -3 1 3 2 q /( q - 1) ) -

- h ( 3 2 ) + ( 3 1 -3 1 3 2 q /( q - 1) ) ln( q - 1) .

В случае 3 _m >0, m = 1,2, полученные средние взаимные информации строго положительны и, следовательно, I ( U ; V 1 V 2 ) >  I ( U ; V 1 ). Поэтому наличие второго канала наблюдения обеспечивает уменьшение условной энтропии в формуле (28) и, следовательно, приводит к уменьшению минимальной вероятности ошибки s M min . В частном случае, когда 3 1 = 0 или 3 2 = 0, имеем I ( U ; V 1 V 2 )= H ( U )=ln q , s M mi n = 0, и нижняя граница (21) совпадает с границей Шеннона. В этом случае M = 1 и канал наблюдения задается одним бесшумным каналом с параметром 3 = 0.

Схема классификации составных объектов, заданных изображениями лиц и подписей

Рассматривается вычисление границы R M ( s ) вида (33) для схемы, содержащей M независимых каналов наблюдения с множествами переходных вероятностей P x _m p, m =1,..., M . Такие каналы образуют составной канал с множеством

P X ^М |Н

.1 c

^P X M p ^{( x} M | «Э = П P X m p ^{( x} m | ^ ) [ ^m =1                       J i =1

условных по классам вероятностей на ансамбле X ^M . Вероятности вида (43) совместно с априорными вероятностями классов, заданными в (9), позволяют вычислить среднюю взаимную информацию I ( Q ; X ^M ) в форме, аналогичной (41):

M

I ( Q ; X ^M ) = H ( X ^M ) - X H ( X m | Q ).           (44)

m =1

Численные реализации границы R_M ( s ) получены для множества Q , содержащего c = 25 классов и ансамбля X 1 X 2 , заданного множествами изображений лиц X 1 и подписей X 2 от 25 персон, по 40 изображений от каждой персоны. Априорные вероятности классов считались одинаковыми. Для описания информативных объектов (лица или подписи) использовались их древовидные представления наборами эллиптических примитивов [12]. Представления получены на основе дихотомического разбиения объектов на непересекающиеся сегменты и аппроксимации сегментов эллиптическими примитивами, которым присвоены средние яркости пикселей соответствующих сегментов. Центры и радиусы примитивов вычислены с использованием центральных и осевых моментов инерции аппроксимируемых сегментов. Структура таких представлений схожа с иерархической структурой, предложенной в [13]. Различие объектов на множестве их древовидных представлений измерялось расстоянием, введенным в [14].

Примеры древовидных представлений лица и подписи, заданных полутоновыми изображениями размера 256×256 с 256 уровнями яркости, даны на рис. 3. В приведенных примерах показаны многоуровневые представления, которые содержат по 2 ^l эллиптических примитивов на уровнях l =0,1, . , 8. В таких представлениях примитивы соответствуют вершинам l -го уровня в бинарном дереве. Параметры примитива нулевого уровня используются для нормировки параметров примитивов последующих уровней. Эллиптические примитивы всех уровней строятся в собственных координатных осях представляемого объекта, а их параметры нормируются относительно параметров примитива нулевого уровня. Указанные операции обеспечивают инвариантность таких представлений к сдвигу, повороту, масштабу и яркости объектов. Для кодирования параметров примитивов (координат центров, радиусов и уровней яркости) использован 8-разрядный двоичный код.

На множествах лиц и подписей X m , m = 1,2, введены условные по классам вероятности

P x m p ( x m | ГО ) =

exp ( -v m D ²( x m , x m ) ) /-----------------------?, . = 1,

X exp ( -v m D ²( x m , x m ) )

x m eXm c, (45)

которые соответствуют переходным вероятностям независимых каналов наблюдения в (43). Здесь D2(xm, x m) – квадрат расстояния между предъявля- емым объектом xm∈Xm и «центральным» представителем»

x im = arg min ∑     D ²( x m , x ˆ m )

xm∈Xim xm∈Xim подмножества Xim ⊂ Xm i-го класса, а vim > 0 – свободный параметр. В общем случае расстояния D (xm, xim) вычисляются в выбранном пространстве представлений объектов. Для древовидных представлений множества лиц X1 и множества подписей X2 использовались расстояния с квадратичным ядром, значения которых заданы матрицами смежности, размещенными на ресурсах [15] и [16].

Условные по классам вероятности вида (45) порождают на ансамбле X 1 X 2 условные вероятности

P X ₁ X ₂ | _Ω ( x 1 , x 2 | ω i ) = P X ₁ | _Ω ( x 1 | ω i ) P X ₂ | _Ω ( x 2 | ω i )

и безусловные вероятности

P X ₁ X ₂ ( x 1 , x 2 ) = ( 1 c ) ∑ ^c P X ₁ X ₂ |Ω ( x 1 , x 2 | ω i )

i =1

для любой пары объектов x 1 ∈ X 1 и x 2 ∈ X 2 . Указанные вероятности дают энтропии

H ( X ₁ X ₂ ) =- ∑∑ P _{X 1 X 2} ( x ₁ , x ₂ )ln P _{X 1 X 2} ( x ₁ , x ₂ ),

X 1 X 2

c

H(Xm|Ω)=-(1c)∑∑PXm|Ω(xm|ωi)lnPXm|Ω(xm|ωi) i=1 Xm для вычисления средней взаимной информации (44) при M = 1 и M =2. Параметры vim >0, i =1,…, c, в распределениях (45) на множествах Xm, m =1,2, выбраны из условия R(ε(mсa)x) =0 в точке ε(mca)x =(c-1)c, когда M = 1. В случае M ≥ 1 средней взаимной информации I (Ω; XM) соответствует минимальная вероятность ошибки (39), вычисляемая при значениях условной энтропии H (Ω | XM) =ln c – I (Ω; XM).

Численные реализации границы R M ( ε ) вида (33) на множествах X 1 , X 2 и на ансамбле X 1 X 2 представлены сплошными кривыми на рис. 4. Полученные границы демонстрируют уменьшение потенциально возможной вероятности ошибки классификации на ансамбле по сравнению с аналогичными значениями вероятности ошибки для объектов одной модальности. Для сравнения пунктиром дана реализация нижней границы Шеннона.

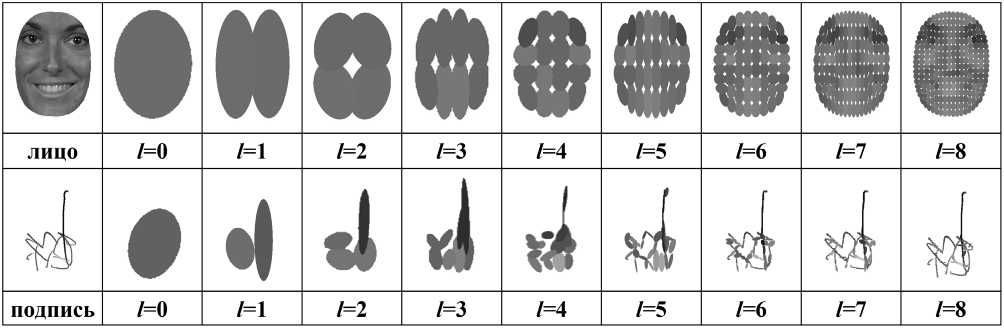
Рис. 3. Примеры представлений лица и подписи бинарными деревьями эллиптических примитивов

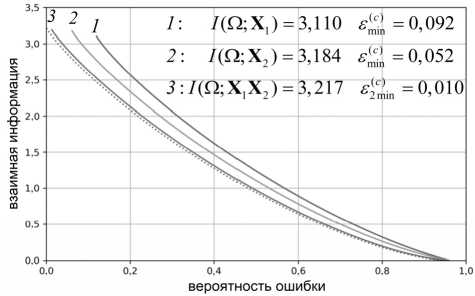
Рис. 4. Реализации границы RM(ε) на множествах лиц (1), подписей (2) и на ансамбле (3)

Следует отметить, что параметры эллиптических примитивов входят в расстояния, которые используются в распределениях вида (45). Поэтому значения средней взаимной информации и минимальной веро- ятности ошибки в границе (33) зависят от длины кодовых описаний указанных параметров.

Предложенный подход позволяет получить реализации функции R M ( ε ) на множествах объектов в виде сигналов или изображений, для которых используются различные представления с известными метриками. Допускается объединение в ансамбль размера M ≥ 2 множеств объектов с различными представлениями. Для выбранного пространства представлений обратная функция от R M ( ε ) дает нижнюю границу вероятности ошибки распознавания образов, порождаемых отдельными источниками ( M =1) или ансамблем источников ( M >1), при фиксированном количестве анализируемой информации.

Заключение

Для модели кодирования дискретных сообщений, переданных по составному каналу с шумом, и модели распознавания образов, заданных наборами объектов различной модальности, получены зависимости наименьшей средней взаимной информации между предъявляемыми данными и возможными решениями от заданной допустимой вероятности ошибки. Найденные зависимости сформулированы в форме монотонно убывающих функций «взаимная информация-вероятность ошибки», которые являются обобщениями известной в теории информации функции «скорость-погрешность» (rate distortion function), когда погрешность измеряется в метрике Хемминга.

Приведенные соотношения получены для схем с составными каналами наблюдения, выходные данные которых образуют ансамбли. Для рассмотренных моделей кодирования и классификации продемонстрировано уменьшение минимальной вероятности ошибки с ростом средней взаимной информации между входом и выходом канала наблюдения при увеличении размера ансамбля предъявляемых данных. Этот результат проиллюстрирован примерами функции «взаимная информация-вероятность ошибки» для схемы кодирования независимых равновероятных сообщений, в которой составной канал наблюдения задан парой симметричных каналов без памяти. Аналогичный эффект продемонстрировали численные реализации функции «взаимная информация-вероятность ошибки» для схемы распознавания изображений лиц и подписей в пространствах их древовидных представлений и на ансамбле таких представлений. Необходимо отметить, что предложенный подход допускает вычисление теоретикоинформационных нижних границ вероятности ошибки классификации в пространстве векторных представлений предъявляемых данных, которые применяются в нейронных сетях.

Независимость полученных соотношений от решающих алгоритмов позволяет использовать их для анализа эффективности алгоритмов кодирования и классификации в терминах избыточности вероятности ошибки алгоритма относительно граничных значений при фиксированных значениях скорости кода или энтропии оценок классов. Планируется исследовать избыточность вероятности ошибки для алгоритмов кодирования дискретных источников и алгоритмов распознавания образов с разделяющими функциями различного вида.

Работа выполнена при поддержке Министерства науки и высшего образования в рамках выполнения работ по Государственному заданию Федерального исследовательского центра «Информатика и управление» РАН.