Теоретико-экспериментальные исследования прототипа резонаторного сверхвысокочастотного ионного двигателя для космических аппаратов

В настоящее время, в связи с широким применением беспилотных космических аппаратов микро- и нанокласса, актуальной проблемой является создание эффективных двигательных систем для данной категории аппаратов. Ключевым параметром таких двигательных установок является возможность работы при низком уровне потребляемой электрической мощности. Авторами данной работы была предложена концепция ускорительного сверхвысокочастотного (СВЧ) ионного двигателя (ИД) с суммарным энергопотреблением не более 10 Вт. Основными особенностями концепции являются:

• •    ускорение ионов осуществляется не постоянным, а переменным высокочастотным (ВЧ) или СВЧ-полем;

• •    источником ВЧ/СВЧ-поля является автогенератор на основе твердотельных СВЧ-элементов;

• •    источником ионов является высокочастотный ёмкостный разряд, а их ускорителем — избыточная электромагнитная энергия, не поглощённая высокочастотным ёмкостным разрядом;

• •    пространственное разделение избыточной электромагнитной энергии на электрическую и магнитную составляющие осуществляется посредством тороидального резонатора (ТР) (по типу клистрона);

• •    повышение электрической напряжённости ВЧ/СВЧ-поля осуществляется за счёт приближения резонансной частоты ТР к основной частоте автогенератора (в этом случае увеличивается добротность колебательного контура);

• •    ускорение переменным электрическим полем предполагает отсутствие нейтрализатора положительного заряда, так как в процессе работы из сечения

двигателя попеременно выбрасываются положительные и отрицательные компоненты плазмы.

На материально-технической базе научно-исследовательской лаборатории «Двигательные установки микротяги малых космических аппаратов» ОмГТУ был разработан и изготовлен первый прототип ускорительного ВЧ/СВЧ ИД с комбинированной последовательной схемой ускорения ионов: после разрядной камеры была установлена классическая ионно-оптическая система (ИОС) с постоянной разностью потенциалов, после неё — ускоряющий зазор тороидального резонатора. Суммарное энергопотребление прототипа составляет 8 Вт. Изначально предполагалось, что для входа ионов в ускоряющий зазор с ВЧ/СВЧ-полем необходимо предварительное ускорение в постоянном электрическом поле. Наличие ИОС с постоянной разностью потенциалов должно было обеспечить такое время прохождения пучка ионов, которое соответствовало бы ускоряющему периоду синусоидального переменного напряжения. В дальнейшей работе авторов было определено, что наличие классической ИОС в конструкции не требуется. В настоящее время авторами разработаны безэлект-родные (ИОС в классическом исполнении отсутствует) прототипы ускорительных ВЧ/СВЧ ИД.

Для подтверждения работоспособности концепции ускорения ионов в зазоре ТР требовался экспериментальный метод определения скорости ионов в струе.

В мировой практике экспериментального определения скорости и энергии заряженных частиц находит применение времяпролётный метод. В англоязычной литературе данный метод известен как TOF (Time-of-flight). Авторы работы [1] применяют данный метод для оценки эмиссии электронов, индуцированных импульсными ионными пучками. Конструкция времяпролётной установки представляла собой трёхэлектродную систему, где средний электрод выполняет функцию фильтра ионно-индуцированных вторичных электронов, а третий электрод является позиционно-чувствительной микроканальной пластиной — детектором для одновременного обнаружения фотонов, электронов и ионов. В работе [2] время-пролётный метод положен в основу миниатюрного массового спектрометра для анализа источника ионного пучка. Рабочая полость установки состоит из удвоенной области импульсного ускорения, области бесполевого дрейфа, отражателя и детектора ионов. Ионы, находящиеся в зарядовом состоянии, имеют одинаковую кинетическую энергию в ортогональном направлении. При этом тяжёлый ион имеет меньшую скорость, чем лёгкий. Авторами работы [3] данный метод применялся для оценки производительности ионного электрораспылительного двигателя.

С целью определения выходных характеристик прототипа ВЧ/СВЧ ИД коллективом авторов были применены методы измерения скорости, энергии и т. д. [4–6].

В рамках времяпролётного метода осуществлялось измерение величины скорости ионизированного газа, истекающего из рабочей полости прототипа ИД. Экспериментальные исследования показали нетипичные значения для однозарядного режима генерации ионов скорости между датчиками времяпролётного канала [4].

Для понимания нетипичных значений скоростей ионов для однозарядного режима генерации было сделано предположение, что в результате включения ИОС образуются многозарядные ионы за счёт появления электронной лавины. Разброс времени пролёта ионизированного газа можно объяснить действием переменного уско-ряющего-замедляющего напряжения в зазоре ТР [4].

Целью данной работы является исследование работы прототипа резонаторного ВЧ/СВЧ ИД в части определения скорости ионизированного потока рабочего тела и анализа ускоряющей системы на основе теории многоэлектродных вакуумных ламп с замещением электронного тока на ионный [7].

Постановка задачи исследования

Задачи теоретико-экспериментальных исследований резонаторного ВЧ/СВЧ ИД состоят из:

• •    разработки математической модели для исследования процессов подвода энергии частицам внутри прототипа ИД и потерь энергии частиц при взаимодействии их с газовой мишенью за пределами прототипа;

• •    проведения экспериментальных исследований в части определения величины тока ионного пучка и скорости ионизированного газа;

• •    анализа численных и экспериментальных результатов исследований.

Теория

Объектом исследования является прототип резонаторного СВЧ ИД (рис. 1), состоящий из двух соосно расположенных цилиндрических резонаторов 1 и 2 , которые образуют ТР ИД диаметром 140 мм и длиной 70 мм. Принцип ускорения рабочего тела — ступенчатый: первая ступень — ускорение в постоянном электрическом поле; вторая ступень — дальнейшее ускорение в переменном электрическом поле. Во внутреннем цилиндрическом резонаторе расположены сетчатый ёмкостный генератор плазмы (сетка № 1) и две перфорированные пластины (сетки № 2 и 3) ИОС. На сетки № 2 и 3 подаётся постоянное напряжение. Перед генератором плазмы расположена пластина-анод, на которую подаётся низкий положительный потенциал. Во внутреннем цилиндрическом резонаторе в торцевой стенке установлена сетка № 4. В наружном цилиндрическом резонаторе установлена сетка-катод.

ВЧ/СВЧ-энергия подводится к генератору плазмы через двухпроводную линию, проходящую через полость ТР. При генерации плазмы происходит возбуждение ТР. Согласно теории возбуждения объёмных резонаторов, в ТР происходит пространственное разделение электрического поля, которое концентрируется в зазоре между торцевыми крышками резонатора, а магнитное поле вытесняется в пространство между цилиндрическими оболочками. Переменное электрическое поле между сеткой № 4 и катодом оказывает ускоряющее воздействие на заряженную частицу, попавшую в зазор. Для вытягивания ионов ВЧ/СВЧ-плазмы в ускоряющий зазор установлены анод, сетки № 1–4 и катод. Таким образом, источник плазмы одновременно является и её ускорителем. Постоянные источники напряжения U1 и U2 соединены согласно рис. 1. Для реализации время-пролётного метода определения скорости ионов в схему прототипа введён ключ к1, позволяющий отключать ИОС постоянной разности потенциалов. Принцип работы датчиков ионов времяпро-лётного стенда основан на подаче сигнала при появлении на чувствительном элементе датчика положительного заряда. Так как в прототипе — две независимые системы ускорения, то запуск одновременно двух систем проблематичен. Поэтому измерение скорости ионов осуществлялось при работающей ВЧ-системе

Приведённая на рис. 1 схема рассматривалась как шестиэлектродная лампа [8].

Определение ионного тока много электродной лампы сводится к приве

дению её к эквивалентному

I = GU ^{2 ,} A        д1

диоду:

-

-

где в

U д1

действующее

плоскости сетки

9 ^£ 0

2 q e S A

m   d _a ² _C1

i

№

напряжение

1 (рис. 1);

первеанс диода;

ε ₀ q_e

электрическая

постоянная; m_i ,

масса иона и элементарный заряд

соответственно;

ного электрода, сетки № 1; d _аС1 до сетки № 1.

S A

площадь сплош-

эквивалентная

расстояние

площади от анода

путём однократного включения ИОС постоянной разности потенциалов замыканием ключа к1 . Чтобы избежать срабатывания датчиков при работе только ВЧ-систе-мы, первый датчик располагался на расстоянии 5 см от выходного сечения двигателя. В этом случае фоновое давление тормозило истекающие ионы.

При разработке математической модели процессов, происходящих в газоразрядной камере прототипа резонаторного ВЧ/СВЧ ИД, использовалась теория многоэлектродных ламп.

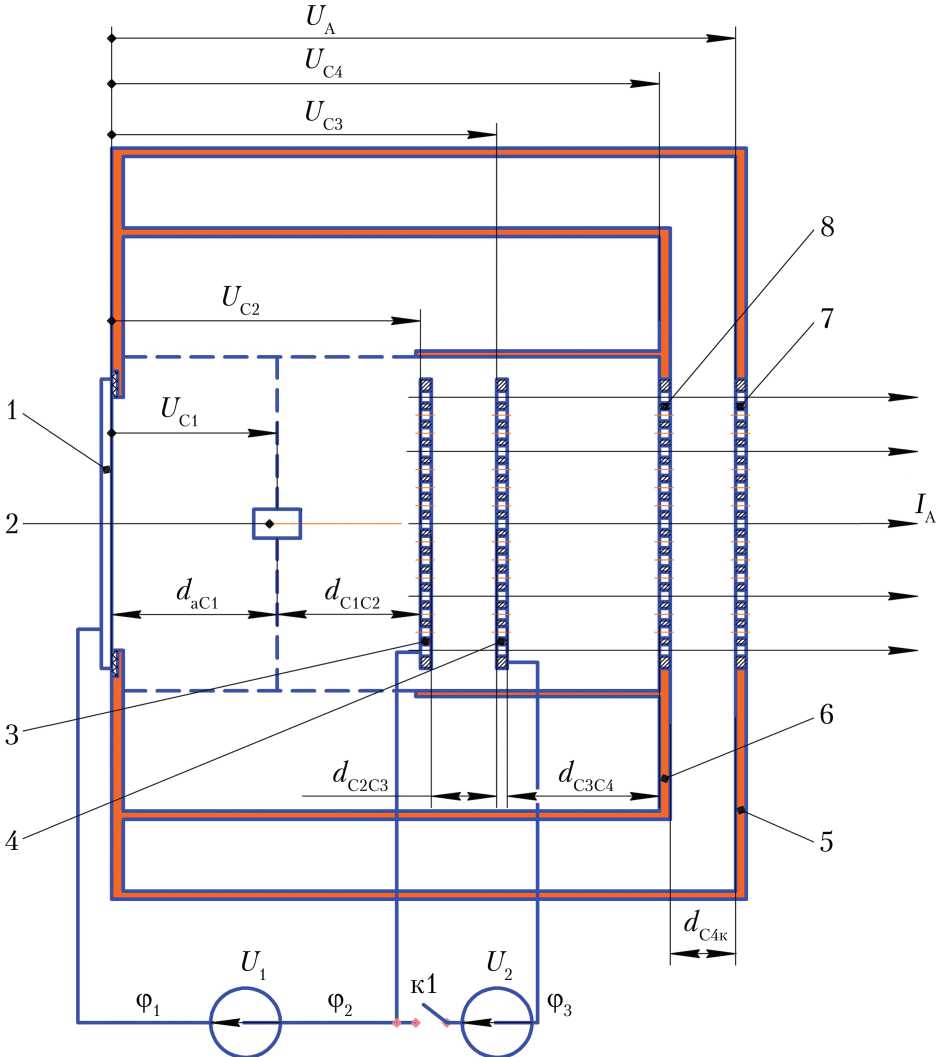
Рис. 1. Принципиальная схема прототипа резонаторного высокочастотного-сверхвысокочастотного ионного двигателя: 1 — анод; 2 — сетка № 1 (генератор плазмы); 3 — сетка № 2; 4 — сетка № 3; 5 — наружный резонатор; 6 — внутренний резонатор; 7 — катод; 8 — сетка № 4; U ₁ и U ₂ — напряжения на источниках питания; к1 — ключ; ϕ₁ , ϕ₂ и ϕ₃ — потенциалы на электродах ИОС; U _C1 , U _C2 , U _C3 , U _C4 и U _А — напряжения на электродах; d _аC1 , d _C1C2 , d _C2C3 , d _C3C4 и d _C4к — зазоры между электродами; I _А — ток ионного пучка (рисунок создан авторами)

Для определения ионного тока I _А , напряжения на сетках U _{C i} определяются относительно анода (для электронного тока — относительно катода).

Действующее напряжение в плоскости i -ой сетки можно определить по выражению (при приведении к эквивалентному аноду):

U д i = σ i ( D i U д ( i –1) + U C i + D i ′ U д ( i +1) ), (2)

где U _{C i} — напряжение i -й сетки; U _{д ( i –1)} , U _{д ( i +1)} — действующие напряжения в плоскости соседних сеток; D_i , D_i ′ — прямая и обратная проницаемости i -й сетки в предположении, что ( i + 1)-я и ( i – 1)-я сетки заменены сплошными проводящими поверхностями;

n _i = i ₊ d ₊ d, - острота управления.

Прямая проницаемость показывает, насколько слабее электростатическое воздействие на поле перед катодом потенциала анода, по сравнению с воздействием потенциала сетки.

Обратная проницаемость показывает, насколько слабее электростатическое воздействие на поле перед анодом потенциала катода, по сравнению с воздействием потенциала сетки [8].

Тогда можно получить систему уравнений для определения действующего напряжения на сетке № 1 из выражения (1) (при приведении к эквивалентному катоду):

U _Д1 = ^( U C! ⁺ D 1 U д2 );

U д2 = " ₂ ( D 2 U д! ⁺ U C2 ^{+ D} 2 ^U^

^U д3 = * 3 ( D 3 ^U д2 ^{+ U} C3 ⁺ D 3 ^U д4 );

^U д4 = ^C D 4 ^U д3 ^{+ U} C4 ⁺ D 4 ^U A )'

В общем случае прямую и обратную проницаемости можно определить, зная параметры сетки — p (шаг плетения сетки) и с (радиус проволоки сетки):

-Wna,,) p

D' =----,

2 л d_r Cк

2 с где a C — параметр сетки, a C = -^—; d _aC — расстояние от анода до сетки; d _Cк — расстояние от сетки до катода.

К перфорированным пластинам электродов ИОС и торцевых стенок резонаторов был применён метод определения проницаемостей на основе плетёных сеток. Все электроды выполнены с одинаковыми апертурами.

Напряжения относительно анода равны:

UC1 = ϕ1 – ϕВЧ/СВЧ, где ϕВЧ/СВЧ = 2 EВЧ/СВЧ . s, где EВЧ/СВЧ — напряжённость поля в высокочастотном зазоре; s — длина зазора, s = 0,001 м; UC2 = ϕ1 – ϕ2; UC3 = ϕ1 – ϕ3 = ϕ1 + U2

( U _C3 — величина, переменная при подъёме напряжения на источнике U ₂ );

U _C4 = ϕ ₁ – ϕ _ВЧ/СВЧ ;

UА = ϕ1 – ϕВЧ/СВЧ = ϕ1 ± 2 , где U — величина напряжения переменного поля зазора ТР.

С использованием выражений (4) и (5) определялись проницаемости сеток. Проницаемости сеток являются малыми величинами из-за большого расстояния между ними.

Решая систему уравнений (3) последовательным раскрытием скобок, можно отбросить величины с третьим порядком малости (компоненты, содержащие произведение трёх величин проницаемостей).

Тогда величину действующего напряжения в плоскости сетки № 1 можно определить по следующей зависимости:

U д1

_{g l} ( U ci + | D J U _C2 a ₂ )

1 - a 1 o ₂ D 1 D ₂

Для сравнения полученного ионного тока с максимальным выводимым из плазмы током можно воспользоваться выражением из работы [6]:

^T e – ¹

I = qNS k e ² , A max е i A m

i

D =

-1п( ла _с ) p

2 л d „ aC

где N_i — концентрация ионов (из результатов зондовых исследований);

k — постоянная Больцмана; T_e — электронная температура (из результатов зондовых исследований); m_i — масса иона (для случая азотной плазмы — половина массы молекулы).

Ионный ток диода определяется следующим выражением:

от катода ИОС до датчиков Д1 и Д2 соответственно.

В свою очередь, энергия частицы равна

m .9 2

E = ₂ ⁱ ,

¹A 0    9 S

² q e S ^i ^- ^): m_i ( d _aC1 + d _C1C2 ) ^{2 ,}

где ϑ — скорость частицы на выходе из ТР.

Скорость частицы на выходе из ТР есть величина непостоянная и зависящая от фазы переменного поля в момент входа частицы в этот зазор:

где S _пов — площадь электрода ИОС (см. рис. 1, поз. 3 ).

При разработке математической модели по определению скорости ионизированного газа между произвольно выбранными реперными точками использовалась теория электромагнитного взаимодействия заряженной частицы с веществом.

Скорость, регистрируемая между реперными точками (датчиками), есть следующее отношение из работы [4]:

э

L _Д

Д

t ₂ – t ₁ ^,

где L _Д — расстояние между датчиками; t ₁ и t ₂ — время между моментом выхода ионизированной частицы из ТР и достижения ей первого датчика, расположенного на расстоянии L _Д1 от резонатора, и моментом выхода

и достижения второго датчика, расположенного на расстоянии L _Д2 от ^L Д1               ^L Д2

резонатора, 1 1 = "^— и 1 2 = -^— ; З Д1

и ϑ _Д2 — скорости частиц у датчиков Д1 и Д2 соответственно.

Из выражения кинетической энергии частицы можно следующим образом выразить скорости частиц:

W-^)

^Д ¹    V         m.       ’

i

$ = $ _вх ⁺

2 qzU sin( ^T + ф )

m i

где z — величина многозарядности иона; U — величина напряжения переменного поля зазора ТР; τ — пролётный параметр (количество циклов смены направления поля в зазоре длиной d _С4к при прохождении его частицей со

C4kVTOp скоростью Звх), т - ——---; vmop — частота вх поля в ТР; ϕ — фаза поля в момент входа частицы в высокочастотный зазор.

Скорость входа частицы в высокочастотный зазор обусловлена энергией Т , переданной ей постоянным полем в зазорах d _aC1 + d _C1C2 и d _C2C3 и потерями энергии в зазоре d _C3C4 , который является металлической пролётной втулкой, лишённой переменного и постоянного полей. Другими словами, между пространством ускорения постоянным электрическим полем (зазоры d _aC1 + d _C1C2 и d _C2C3 ) и пространством ускорения переменным электрическим полем (зазор d _С4к ) присутствует участок, где частицы не испытывают воздействий, кроме торможения в газовой мишени зазора d _C3C4 . Тогда

вх

2( Т — A E , S 3 )

m i

$ Д2

² ( ^E — A ^E _{Е Д2} )

m i

где E — энергия частицы при выходе из ТР; Δ E _{∑ Д1} и Δ E _{∑ Д2} — суммарные потери энергии частиц при движении через остаточный нейтральный газ в вакуумной камере на расстоянии

где Δ E _{∑ S 3} — суммарные потери энергии частицы в зазоре d _C3C4 .

Энергия частицы при входе в зазор d _C3C4 равна сумме энергий, приобретённых частицей от поля зазора d _aC1 + d _C1C2 и поля зазора d _C2C3 :

T = T U 1 + T U 2 ,                          (15)

где T_{U 1} — энергия поля зазора d _aC1 + d _C1C2 , приходящаяся на одну частицу,

U 1

T =    ; ω — плотность энергии

U 1                    U 1

между электродами с потенциалами ϕ ₁

и    ϕ ₂    при закрытом ключе к1 ,

® u 1

i_ _s Г ф i ^{- ф} '

2      ^d aC1 + ^d C1C2

концентрация

ионов; T_{U 2} — максимальная энергия частицы в поле с напряжением между электродами U _ИОС (в зазоре d _C2C3 ), T U 2 = zq e U 2 .

Частицы двигаются в зазоре d _C2C3

со

скоростью

» 0 =

2T

U 1

m i

и пересекают

^d C2C3

зазор за время t ₀ =      . Количество

^ 0

частиц, одномоментно находящихся в зазоре, можно определить по следующему выражению:

n

^I A0 ^t 0

i заз

q e V заз

T заз – T U 2 – q e

z

^ I > 0, i = 2

где I_i — потенциал ионизации атома рабочего газа. Предполагается, что в зазоре воздействию ударной ионизации подвергаются однократно ионизированные в высокочастотном ёмкостном разряде атомы ( z = 1).

Выражение (17) показывает, что энергии поля должно хватить на создание многозарядного иона и ускорение его вдоль зазора. По данному выражению для каждого напряжения U _ИОС определяется значение z .

С целью определения удельных потерь энергии на взаимодействие заряженной частицы с нейтральным газом (газовая мишень) расчитывается течение ускоренного ионизированного газа за ИОС. Расчёт удельных потерь энергии проводился для движения частиц в зазоре d _C3C4 и на выходе из ТР до датчиков Д1 и Д2.

где V _заз — объём зазора.

Таким образом, в момент замыкания ключа к1 и перехода диодного режима работы прототипа ИД к многоэлектродному режиму в зазоре d _C2C3 концентрация ионов составляет величину n_{i заз} .

В многоэлектродном режиме работы прототипа ИД энергия поля, приходящаяся на одну частицу, равна

T

заз

• ^{1    b} 0 ^U 2

.

• 2    n ci

n i заз     C2C3

Часть данной энер-

Процессы взаимодействия ионизированных частиц с газовой мишенью носят электромагнитный характер. Их можно классифицировать с точки зрения классической физики на основе представления о параметре удара (прицельном параметре или параметре соударения) b , т. е. расстоянии наибольшего сближения частиц [9, 10].

При взаимодействии частиц с атомами среды, через которую они летят, сопоставляется величина параметра удара b с размером атомов a . В зависимости от того, как соотносятся между собой величины b и a , происходит тот или иной процесс взаимодействия [9, 10]. В случае b ~ a сильны явления упругого рассеяния, поляризации нейтрального газа по пути движения ионов и ионная перезарядка [11].

Потери энергии на упругое взаимодействие ионов с газом в зазоре d _C3C4 можно определить по следующему выражению [10]:

гии идёт на ускорение заряженной частицы вдоль зазора и резистивное тепловыделение. Остальная часть в результате электронного удара при замыкании ключа к1 может привести к возникновению многозарядных ионов на входе в зазор d _C3C4 . Оценить степень многозарядности при различных значениях U _ИОС можно по следующему соотношению:

A e „ = A В nt In упр. S 3            S 3 ат

2a 2 b bS3

^d C3C4^,

где ab  — параметр экранирования, a0

a_b =         ; Z — заряд ядра мишени;

z ^{2 3} + Z ^{2 3}

a ₀ — радиус первой боровской орбиты,

^S 0 h²

a ₀ =      ₂ ; m_e — масса покоя электрона;

^meqe h — постоянная Планка; bS3 — расстояние наибольшего сближения налетающей частицы и ядра атома (молекулы), zZqe2

b_{S 3} =      ; N _ат — концентрация нейт-

4 Л T S o

^P заз ральных частиц в зазоре, N _ат = N _{A RT} ; газ

N _А — число Авогадро; P _заз — давление газа в зазоре d _C3C4 ; R — универсальная газовая постоянная; Т _газ — температура нейтрального газа; Т — энергия ионизированной частицы.

Потери энергии на ионную перезарядку можно определить по следующему выражению [12, 13]:

^E nep S = ^F q ^N аХот ⁺ ^

( m 3 <2 e S 3

^{+ q} e ^{I d} C3C4^{, (19)}

где   Fq   — равновесные зарядовые фракции; σпот, σзахв — сечения потери и захвата одного электрона соответственно; 9 23 — квадрат скорости входа иона в газовую мишень (скорость 2T на выходе из зазора d„„ „,), 92, = ——;

C2C3       S 3     m

i

I — средний потенциал ионизации атома газовой мишени, I = 13,5 Z .

Зарядовые фракции описывают распределение ускоренных ионов и соответствуют относительному количеству ионов с зарядом q [14]. В простом случае F_q можно выразить безразмерную ширину зарядового пределения в ионном пучке d _расп :

d ²

распр

^{Fq =} ( z – q ср ) ^{2 .}

через рас-

Здесь ширина зарядового распределения равна [15]

распр

q ⁵³ q ср          ср

Z      4 ^.

В формулах (20) и (21) средний заряд ускоренного иона для газа можно найти по следующему выражению из работы [16]:

q ср

376 X + X ⁶

1428 + 1206 X ² + 690 X + X ⁶

где X =

_Z 0,03 – 0,17 Y _Y

1+ Z-

; Y =

Z ^-0^ S 33

, здесь

V ₀

V ₀ — атомная единица скорости (скорость орбитального электрона в атоме водорода), V ₀ = 2,188·10⁶ м/с.

Для скоростей частиц, меньше значений ZV ₀ , сечения потери и захвата электрона можно вычислить по следующим полуэмпирическим выражениям [17]:

а _пот = л а

₀ 2 Z 2 Z _я 4

2 19 р S 3 У

45 ZV 0

;

<5

захв

= л а 2 Z ²

^ 5 3

ZV 0

,

где Z _я — заряд ядра бомбардирующего иона.

Потери энергии на поляризацию атомов/молекул нейтрального фонового газа можно определить по следующему выражению:

ΔE пол.S3

^{= σ} пол ^N ат ^Td C3C4^,

где σпол — сечение поляризации для среднего

заряда иона,

₌ / «О Р

^ р 2ns ₀ Т ’

здесь α — поляризуемость разреженного газа.

Поляризуемость разреженного газа можно определить по выражению Клау-зиуса–Моссотти через относительную диэлектрическую проницаемость газа:

а =

I s — 1

к ^s + 2 j

4 л N _ат '

Диэлектрическую проницаемость разреженного газа ε можно определить через диэлектрическую восприимчивость χ :

ε = 1 + 4 π N _ат χ .

Диэлектрическую восприимчивость газа в выражении (27) можно получить, используя диэлектрическую проницаемость газа при другой концентрации.

Суммарные энергетические потери в зазоре d _C3C4 равны

Δ E _{∑ S 3} = Δ E _{упр. S 3} + Δ E _{пер. S 3} + Δ E _{пол. S 3} . (28)

Суммарные потери энергии на выходе из ТР Δ E _{∑ Д1} и Δ E _{∑ Д2} определяются аналогично потерям энергии в зазоре d _C3C4 по выражениям (19) – (28) со следующими небольшими изменениями:

• •    в расчёте удельная энергия потерь умножается на расстояния до датчиков L _Д1 и L _Д2 вместо d _C3C4 ;

• •    вместо значения энергии Т в выражение (25) подставляется значение энергии Е из выражения (12). Если энергия Т зависит только от величины постоянного ускоряющего напряжения между электродами ИОС, то энергия Е меняется ещё и от sin(π τ + ϕ );

• •    давление в вакуумном пространстве может отличаться от давления в зазоре d _C3C4 , поэтому требуется корректировка концентрации атомов газовой мишени;

• •    скорость ϑ _{S 3} заменяется на скорость ϑ из выражения (13), которая также зависит от sin( πτ + ϕ ).

Результаты и обсуждения

При достижении низкого давления в вакуумной камере при подаче рабочего тела устанавливалось напряжение на источники U1 и U2 при условии открытого ключа к1 (см. рис. 1). Напряжение на источнике U1 имело постоянную величину и составляло в номинальном режиме 80 В. Напряжение на источнике U2 в процессе эксперимента ступенчато поднималось с шагом 10 В от 100 до 1 200 В. При открытом ключе к1 поджигался ВЧ/СВЧ-разряд. Далее однократным нажатием ключа к1 прототип ВЧ/СВЧ ИД переходил из режима диода в режим шестиэлектродной вакуумной лампы. На расстоянии LД1 = 0,05 м от среза катода ИОС располагался первый датчик ионов Д1, на расстоянии LД2 = 0,15 м от катода ИОС — второй датчик Д2. По разности времени срабатывания датчиков определялась скорость потока ионизированного газа при каждом напряжении источника U2 [1]. При закрытом ключе к1 потенциалы на электродах были распределены следующим образом: ϕ1 = +80 В; ϕ2 = 0 В; ϕ3 = –U2 В (U2 = 100, 110, …, 1 200 В). В качестве рабочего тела использовался азот.

Подставляя значения напряжений и проницаемостей в выражение (6), получим U _д1 = 80,143 В. По выражению (1) ионный ток I_A = 2,324 мкА. Данное значение соответствует значению ионного тока, определённому с помощью цилиндра Фарадея. По результатам замеров ток с цилиндра Фарадея составлял 2…4 мкА при напряжениях U ₁ = 80…200 В. При этом уровень тока никак не менялся при изменении значений напряжения U ₂ .

Процесс ускорения частиц представляется следующим образом. До замыкания ключа к1 плазма, генерируемая на сетках ёмкостного зазора, находится под действием поля источника U1. Концентрация ионов в пространстве зазора daC1 + dC1C2 составляет величину порядка 1016 частиц/м3 [3]. При этом плотность энергии поля невелика, так как расстояние между электродами (daC1 + dC1C2) большое, а номинальное напряжение источника U1 всегда 80 В. При этом установившееся напряжение составляет 4…12 В в зависимости от мощности ВЧ/СВЧ-разряда. До замыкания ключа к1 прототип работает в режиме диода с потенциа- лами электродов, и ϕ2 = – 21 = –40 В.

равными ϕ1 = 21 = 40 В Через ненагруженные электроды ИОС течёт ионный ток величиной IA0, определяемый по выражению (8), его величина составила 4,413 мкА. После замыкания ключа к1 диодный режим работы прототипа переходит в шестиэлектродный режим, ионный ток падает, электронным ударом в пространстве между электродами ИОС постоянной разности потенциалов рождаются многозарядные ионы. В этом случае многозарядные ионы последовательно ускоряются постоянным и переменным напряжением, чем обусловлена аномально высокая скорость ионов, зарегистрированная датчиками времяпролётного стенда. Действием переменного напряжения на ускоренные постоянным напряжением ионы объясняется пилообразный характер экспериментальной и теоретической диаграмм роста скорости ионов при повышении постоянного напряжения на электродах ИОС. То есть, в зависимости от фазы ВЧ/СВЧ-поля при входе иона в ВЧ/СВЧ-зазор может произойти торможение или ускорение частицы.

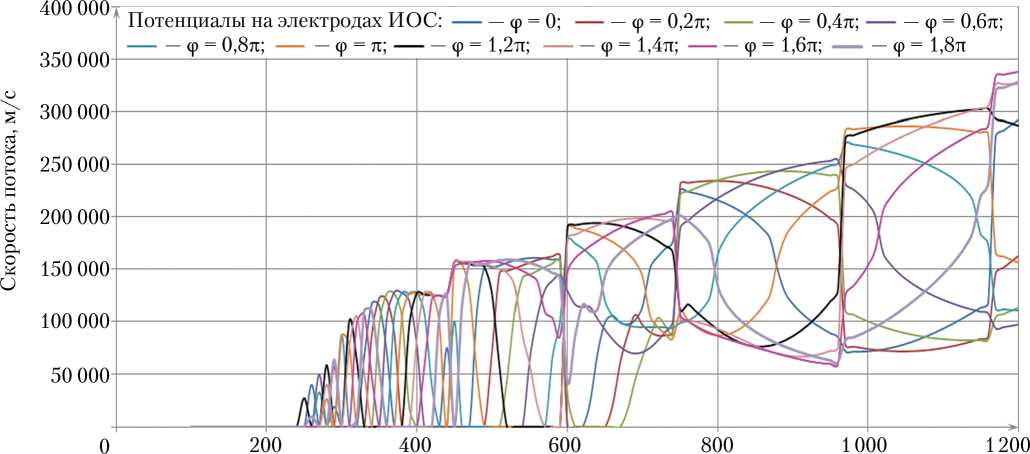
С помощью численных решений уравнений (19) – (28) были получены скорости ионов между реперными точками (датчиками) Д1 и Д2 в зависимости от фазы входа ионов в ускоряющий зазор. Расчёт проводился для следующих значений: ϕ = 0; 0,2 π ; 0,4 π ; 0,6 π ; 0,8 π ; π ; 1,2 π ; 1,4 π ; 1,6 π ; 1,8 π . Результаты численных решений приведены на рис. 2.

Из анализа данных, приведенных на рис. 2, виден разброс скорости ионов, обусловленный разностью фаз входа и выхода частиц в высокочастотный зазор. Диапазон разброса скоростей при максимальном напряжении ИОС 1 200 В составил 100…340 км/с. При напряжении в диапазоне 100…250 В происходит торможение ионов в газовой мишени, и они не достигают чувствительных элементов датчиков. Ступенчатые подъёмы скоростей обусловлены ростом многозарядности ионов по мере увеличения плотности энергии в зазоре d _С2С3 между электродами ИОС.

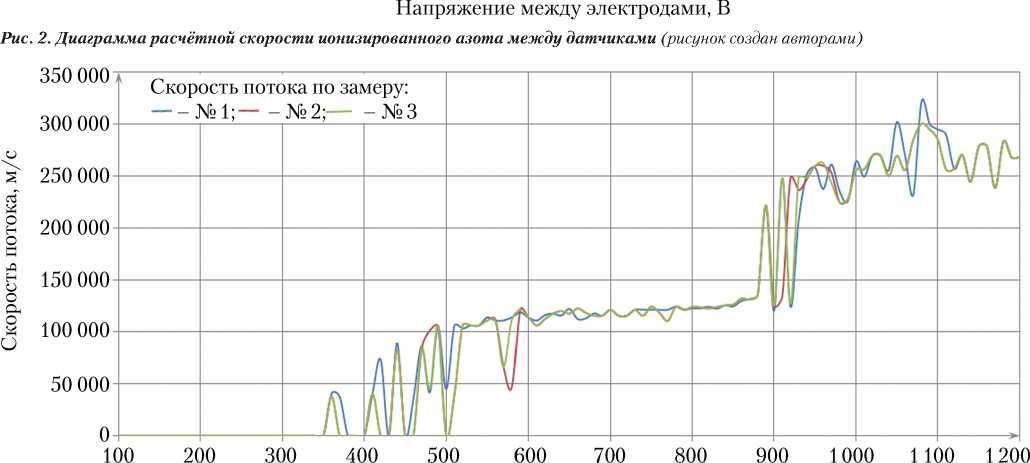
Экспериментальные значения скорости ионизированного азота приведены на рис. 3.

Напряжение между электродами, В

Рис. 3. Диаграмма измеренной скорости ионизированного азота, ускоренного прототипом ИД (рисунок создан авторами)

На рис. 3 видно, что рост скорости начинается с напряжения 350 В. Величина скорости находится в диапазоне 120…130 км/с, и при значениях напряжения от 900 В происходит скачок скорости до 250–320 км/с. В отличие от экспериментальных данных, теоретическая скорость (см. рис. 2) начинает расти с 250 В и ступенчато поднимается до 300–340 км/с при напряжении 1 200 В. Разброс экспериментальных скоростей не так заметен, как разброс теоретических скоростей, так как датчики фиксируют только максимальную скорость. Представленная математическая модель даёт представление о вероятном механизме возникновения аномально высоких значений скоростей ионов при истечении из прототипа ускорительного ВЧ/СВЧ ИД. Показано, что причиной несрабатывания датчиков времяпролётного стенда на напряжениях в ИОС менее 300 В являются потери энергии ионов в фоновом газе. Математическая модель даёт близкие к экспериментальным данным значения максимальной скорости ионов, объясняет причину расхождения значений скорости при нескольких замерах на одном и том же напряжении в ИОС. Приведённая модель не даёт ответ на причину практически прямолинейного участка экспериментальных скоростей в диапазоне напряжений 600…900 В (см. рис. 3). В экспериментальных данных скорость ионов на этом участке соответствует трёхкратной ионизации ионов азота. В то же время, теоретическая кривая на этом участке монотонно возрастает. Возможная причина кроется в одновременном существовании в пространстве между электродами ИОС ионов различной степени многозарядности. Тогда возможны явления ионной перезарядки, когда более многозарядный ион забирает внешние электроны с орбиталей иона с меньшей степенью много-зарядности. При этом происходит усреднение зарядов ионов в струе. При высоких плотностях энергии в зазоре ИОС большинство ионов имеют высокую степень много-зарядности.

Математическая модель ускорительного ВЧ/СВЧ ИД на основе многоэлектродных вакуумных ламп связывает геометрические размеры электродов ИОС и их пространственное расположение с извлекаемым ионным током. Модель показала значение теоретического ионного тока 2,324 мкА, экспериментальные значения по цилиндру Фарадея составили 2…4 мкА.

Выводы

Были проведены теоретико-экспериментальные исследования работы резонаторного ВЧ/СВЧ ИД. Экспериментальные исследования показали, что скорость частицы при одном и том же напряжении в ИОС непостоянна, что указывает на ускоряюще-замедляющее действие переменного электрического поля ускоряющего зазора. Высокие скорости частиц обусловлены рождением между электродами ИОС многозарядных ионов, что и подтверждается математической моделью.

Исследование выполнено за счёт гранта Российского научного фонда № 19-79-10038,