Теоретико-множественный анализ алгебраических систем в задачах распознавания групп по их спектру

Группы, заданные порождающими элементами и определяющими соотношениями, возникают естественным образом во многих областях математики и связанных с нею дисциплин, особенно в некоторых разделах геометрии и топологии.

Комбинаторную теорию групп можно охарактеризовать как теорию групп, которые описываются порождающими и определяющими соотношениями, где в качестве модели используется модель, известная как «комбинаторика слов». Как самостоятельная наука со своей проблематикой она оформилась по существу только после того, как в 1911 г. М. Дэн сформулировал основные алгоритмические проблемы теории групп: проблему распознавания равенства, известную в литературе также под названием «проблема тождества», проблему сопряженности и проблему изоморфизма.

Пусть

G = ( ^ 1 , x 2 ,..., X m I v = e , v 2 = e ,..., V k = e)

– периодическая группа, т. е. группа у которой все элементы имеют конечный порядок, с множеством свободных порождающих { x ₁, x ₂,..., x_m } и { v ₁, v ₂,..., v_k } – определяющими соотношениями в G ; e – единица группы (пустое слово).

В работах [1; 2] был предложен алгоритм, который позволяет моделировать произвольную периодическую группу G, заданную порождающими элементами и определяющими соотношениями посредством последовательности специальных объектов Ks = {Ps, As, Cs, Ts}, каждый их которых представляет собой множество всех слов Ps группы G, не превосходящих по длине s, с заданной на этом множестве таблицей умножения Ts, обраба- тывая которую при помощи алгоритма As, мы получаем список соотношений Cs в группе G.

В результате работы алгоритма строится последовательность объектов

K ₁, K ₂,..., K_s ,...

В случае бесконечности группы G , число объектов K_s также можно построить бесконечное количество.

Если же группа G конечна, то на каком-то конечном шаге s будет иметь место следующее равенство:

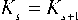
В этом случае последовательность P_s будет представлять элементы группы G , C_s – список определяющих соотношений, а T_s – таблицу умножения в указанной группе.

Теорема 1. Пусть s _e N и s наименьшее со свойством K s = K s + i ,тогда | G | < | P s | [2].

Обозначим через ω( G ) спектр группы G , т. е. множество порядков элементов из G . Например, ю( L 2 (7) = {1, 2, 3, 4, 7} [2]. Группа G из класса X называ-ется распознаваемой в X по спектруω( G ), если любая группа H e X , для которой ю( H ) = ю( G ), изоморфна G .

В «Коуровской тетради» В. Д. Мазуров поместил следующий вопрос [3]: «Распознаваема ли группа L ₂(7) по спектру в классе всех групп?»

В работе [4] был получено положительное решение данной проблемы.

Теорема 2. Если спектр группы G равен {1, 2, 3, 4, 7}, то G = L 2 (7) [4].

В процессе доказательства теоремы 2 требовалось установить конечность ряда групп, заданных порождающими элементами и определяющими соотношениями. В работе [4] указывалось, что конечность рассматриваемых групп была получена в результате компьютерного моделирования, основанного на представленном выше алгоритме, однако сами расчеты не приводились. В настоящей работе данный пробел восполнен и ниже приведен расчет группы, найденные свойства которой были необходимы для доказательства теоремы 2.

Рассмотрим пример моделирования группы.

Теорема3. Пусть G = <  x 1 , x ₂, x ₃ | x 1 ² = x ₂ ² = x ₃ ² = e >  -группа, порожденная тремя инволюциями x 1 , x ₂, x ₃ и

• 1)    ®( G ) с ®( L 2 (7) = {1, 2, 3, 4, 7};

• 2)    произведение любых двух инволюций из G есть 2-элемент, т. е. V v , w е G | vw | = {1, 2, 4}, если | v | = | w | = 2.

Тогда | G | <  2¹⁰ и ю( G ) = {1, 2, 4}.

Доказательство. Построим группу G при помощи алгоритма из работы [1]. Обозначим образующие группы x 1 = 0, x ₂ = 1 и x ₃ = 2 .

1. Строим объект K 1 = { A 1 , P 1 , T , C 1 }. Здесь A 1 - алгоритм поиска и замены соотношений из C 1 ; P 1 = { e , 0,1, 2} -образующие группы. В последовательности P ₁ введем отнош ение порядка, полагая по определению e <  0 <  1 <  2 . Таблица умножения T 1 приведена в табл. 1. C 1 = {0² = e , 1² = e , 2² = e } - список соотношений.

Таблица умножения T ₁

	e	0	1	2
e	e	0	1	2
0	0	00 = e	01	02
1	1	10	11 = e	12
2	2	20	21	22 = e

Таким образом, G - элементарная абелева группа порядка 4. Противоречие с предположением о том, что |210| = 3. К аналогичному результату приводят предположения о том, что |120| = 3 или |201| = 3. Поэтому |120| ■ 3 и |201| ■ 3.

Таблица 2

Таблица умножения T ₇

	e	0	1	2
e	e	0	1	2
0	0	e	2	1
1	1	2	e	0
2	2	1	0	e

Рассмотрим следующий случай. Так как элементы 0, 1,2, 010,020,101,121,202 и 212 являются инволюциями, то, составив из них таблицу умножения, мы получим элементы, порядки которых равны 1, 2 или 4 по условию теоремы. Все различные элементы из таблицы умножения данных инволюций приведены в табл. 3.

Таблица 3

Элементы, порядки которых равны 1, 2 или 4, как результат перемножения двух инволюций

Таблица 1

(10)4 = e	(1021)4 = e	(021010)4 = e
(20)4 = e	(1201)4 = e	(101020) 4 = e
(01)4= e	(1202)4 = e	(101021)4= e
(21) 4 = e	(1210)4 = e	(101202) 4 = e
(02)4 = e	(2010)4 = e	(102121)4 = e
(12)4 = e	(2012)4 = e	(121010)4 = e
(0102)4= e	(2020)4 = e	(121020) 4 = e
(0120) 4 = e	(2021)4 = e	(202010) 4 = e
(0121)4 = e	(2101)4 = e	(202012) 4 = e
(0201) 4 = e	(2102) 4 = e	(202101)4 = e
(0210)4 = e	(2120)4 = e	(202121)4 = e
(0212) 4 = e	(2121) 4 = e	(212010) 4 = e
(1010)4= e	(010212) 4 = e	(212020)4 = e
(1012)4= e	(012020) 4 = e	(212101) 4 = e
(1020)4 = e	(020121)4 = e	(212102)4 = e

Дополним список C ₃ соотношениями из табл. 3. Пусть теперь |210| = 7, тогда в список соотношений C ₃ добавится новое соотношение (210)⁷ = e . Продолжая расчет, получим, что в объекте K ₁₁ последовательность Р_хх = P 1 = { e , 0,1, 2}. При этом таблица умножения T 11 будет такая же, как и табл. 2.

И снова приходим к противоречию с предположением о том, что |210| = 7. К аналогичному результату приводят предположения, что |120| = 7 или |201| = 7. Поэтому |120| ■ 7 и |201| ■ 7.

Рассмотренный анализ доказывает, что слова 210,012, 120,021,201 и 102 не могут иметь порядок 3 и 7. Следовательно, данные слова должны иметь порядок 1, 2 или 4. Это означает справедливость следующих соотношений: (210)⁴= e , (012)⁴= e , (120)⁴= e , (021)⁴= e , (201)⁴ - e и (102)⁴= e . Добавим эти соотношения в C ₃.

• 4.    Переходим к построению K ₄ и последующих объектов K s c учетом соотношений из табл. 3. В конечном итоге получим, что K ₁₃ = K ₁₄, | P₁₃ | = | р ₄ | = 2¹⁰. Затем, используя компьютерные вычисления, проверим, что таблица умножения T удовлетворяет всем групповым свой-

• ствам. Таким образом, последовательность P14 с таблицей умножения T14 образует группу, изоморфную G. Непосредственной пров еркой находим, что ω(G) = {1, 2, 4} . Группа G, порядок которой равен 210, является максимальной группой, удовлетворяющей условиям теоремы. Теорема доказана.

Следствие 1. Пусть (10)²= e , (20)²= e , (21)²= e . Тогда получим, что | G | = 8.

Следствие 2. Пусть (10)²= e , (210)²= e . Тогда получим, что | G | = 16 .

Следствие 3. Пусть (210)²= e . Тогда получим, что | G | = 32. Следствие 4 . Пусть (10)²= e . Тогда получим, что | G | = 64.

Таким образом, проиллюстрированный в статье пример показывает эффективность моделирования периодических групп при помощи указанного выше алгоритма в задачах распознавания групп по их спектру.