Теоретико-сетевой подход при автоматизированном проетировании электронных систем

Существует проблема реальности и ее отражения человеком для анализа, исследования и, в конечном счете, развития жизни. Для этого вводят системы отсчета, координат, в которых числа отражают математическую «тень» реальности. При изменении координат меняются числа (компоненты, проекции), но не сама реальность. Хотя сама независимость объекта наблюдения от наблюдателя является одной из проблем измерений.

В математике ввели цилиндрические, сферические, криволинейные системы координат, в которых один объект имеет разные компоненты. Выбираемые контуры и пары узлов представляют электрические процессы в цепях. Вращающиеся системы координат связаны с ротором электрической машины. В экономике реальные потоки продуктов и денежных средств отражают в разных системах отчетности (планы счетов, вводимые международные стандарты финансовой отчетности, МСФО и т.д.). Понятию реального, измеримого объекта в математике соответствует понятие тензора.

Начиная с середины XIX века, тензоры стали использовать в механике при описании упругих деформаций. Первоначально тензорный анализ называли «абсолютное исчисление». Г. Риччи и Т. Леви-Чивита рассматривали тензорное исчисление как составную часть дифференциальной геометрии. Термин «тензор» ввел В. Фойгт в 1898 г., хотя некоторые приписывают это А. Эйнштейну. Тензоры в электротехнике начал применять Г. Крон.

Суть тензорного метода состоит в признании инвариантности объекта в пространстве (вектора, многомерного объема в геометрии; измеримой величины в физике, технике или экономике). Реальный объект существует независимо от субъективных систем координат наблюдателя, в которых объект представлен компонентами (измерен). Если компоненты при изменении координат преобразуются по линейным законам (матрицей преобразования базиса), то это признак измеримости объекта, который является тензором. Если тензор имеет ненулевые компоненты в одной системе координат, то он имеет ненулевые компоненты в любой системе координат. И, наоборот, если тензор имеет нулевые компоненты в одной системе координат, то он имеет нулевые компоненты в любой системе координат. Т.е., реальный объект не исчезает при изменении координат, и не возникает из ничего.

Обобщением понятия тензора является абстрактная система для процессов и структуры одного типа, а конкретные системы рассматриваются как ее «проекции» в координаты, заданные структурой связей. Это позволяет создать математические сетевые модели в разных предметных областях.

Применение тензорного метода к исследованию сложных систем началось с электрических машин, которые считались столь сложными системами, что для каждого типа создавалась своя теория (а порой и несколько). «Основателем обобщенной теории электрических машин является Г. Крон, который в 30-х годах предложил уравнения обобщенной машины. В последние десятилетия благодаря применению ЭВМ усилиями многих ученых-электромехаников обобщенная теория электрических машин получила дальнейшее развитие. …Большинство успехов в теории и практике электромашиностроения связано с математической теорией электрических машин» [2] ( Копылов , 2000, с. 41).

Обобщенная электрическая машина Крона в минимальной форме реализует процесс электромеханического преобразования потока энергии. Другие электрические машины отличаются от обобщенной машины количеством элементов, осуществляющих этот процесс, и количеством связей между ними. Переход от одной машины к другой задает матрица преобразования, которая показывает, как отличаются структуры соединения машин.

В работе «Единая теория электрических машин» [7] (Kron, 1930) все электрические машины, которые до этого считались несопоставимыми, исследованы с единой точки зрения построения диаграмм, которые показывают величину и направление потоков энергии между различными частями сложной машины. Для этого было применено понятие «свободная энергия» из термодинамики.

Основы тензорной теории электрических машин представлены в статье «Нериманова динамика вращающихся электрических машин» [8] ( Kron , 1934). В 60-тых годах в трудах Японской ассоциации прикладной геометрии данная статья охарактеризована как «сделавшая эпоху». Было введено понятие простейшей (обобщенной) электрической машины из двух элементов – обмоток. Уравнения поведения обобщенной машины Крон получил из уравнений Лагранжа. Тогда уравнения любой машины с другим числом и соединением элементов получаются умножением величин в уравнениях простейшей системы координат (обобщенной машины) на матрицу преобразования C , которая показывает, как соединены обмотки в исследуемой машине. Оказалось, что уравнения электрических машин при стационарном режиме имеют такой же вид, как для неподвижных сетей, при условии, что обычное дифференцирование в уравнении

β ^{d ϕ}α                                                      (1)

ea Rав + dt заменяется ковариантным дифференцированием, δ/dt, при котором учитывается изменение вектора при его параллельном переносе вдоль кривой в римановом пространстве:

β δϕ α ,                                             (2)

e a       ae i dt где e – напряжение, R – сопротивление (резистанс), i – ток, ϕ – магнитный поток, t – время, а δϕα/dt – ковариантная производная, учитывающая изменение вектора при параллельном переносе в криволинейном римановом пространстве. При малых колебаниях около стационарного вращения – качаниях, это уравнение принимает вид:

5 e _a = R a_P 5 i ^e + L ae ‘"di ) + K _SYea i ⁵ i ^e dx + R _aPY i ^в dx ^Y , (3)

где R αβγ – тензор третьего ранга, определяемый сопротивлениями, а K δγβα – тензор кривизны Римана – Кристоффеля, наличие которого показывает, что поведение вращающейся электрической машины в режиме качания описывается как движение представляющей точки в неримановом пространстве с асимметричной связью (с кручением).

Форма уравнений для стационарного режима, ускорения и качаний остается одна и та же , но само пространство усложняется за счет все большего искривления. Искривление пространства, представляющего поведение машины, подобно искривлению физического пространства вблизи тяготеющей массы, которое отклоняет луч света (поток фотонов) проходящий мимо поля солнечного тяготения. А. Эйнштейн считал, что Крон распространил в область техники идеи общей теории относительности. Н. Винер отметил, что Крон ввел новый язык, который позволяет не только поставить задачи расчета машин единым образом, но и дать новые методы решения таких задач [11] ( Wiener , 1936).

Крон исследовал преобразования токов и напряжений при изменении соединения ветвей в цепи (circuit, этот термин Крон использовал наряду с термином «сеть» – network). Для этого он ввел понятие простейшей (из отдельных ветвей) сети. Другие сети из данных ветвей – это варианты соединений ветвей простейшей сети [4] ( Крон , 1978). Для получения уравнений соединенной сети из уравнений простейшей сети использовались матрицы преобразования, которые связывают токи в контурах простейшей сети с токами в контурах соединенной сети (или напряжения на свободных ветвях с напряжениями в разомкнутых путях связанной сети). Они представляют матричную запись законов Кирхгофа.

Крон утверждал, что при соединении ветвей рассеиваемая мощность в электрической цепи не меняется – поскольку остаются прежними источники тока и напряжения, которые задают в сети поток энергии. Постулат об инварианте мощности позволял получить тензорную формулу преобразования напряжения – важнейший пункт тензорного анализа сетей. Однако известно, что мощность меняется при изменении связей . Доказано, что для заданной цепи, состоящей из резисторов и источников, величина напряжения на всех резисторах не выше суммы величин напряжений на источниках. Это следует из теоремы Волавера в теории графов о неусилении мощности в резистивной сети. Суть доказательства в том, что в ориентированном графе каждое ребро находится либо в ориентированном цикле, либо в ориентированном сечении, либо отсутствует в обоих.

Под расчетом цепи понимается вычисление электрических величин или их отношений при заданных схеме и параметрах цепи. В частности, задача состоит в определении откликов в соединенных ветвях при заданных воздействиях в отдельных ветвях. При этом должны выполняться законы Кирхгофа о равенстве нулю суммы токов в каждом узле и равенстве нулю суммы напряжений в каждом контуре.

Суть тензорного метода Крона в электротехнике в том, что к уравнениям процесса прохождения электрического тока добавлено описание структуры связей с помощью матриц преобразования. Токи i ^α и напряжения e α на n ветвях связаны законом Ома: e α = z αβ i ^β , где z αβ – матрица комплексных сопротивлений, которая при индуктивном взаимодействии ветвей может и не быть диагональной ( α , β = 1,…, n ).

Контурный метод и узловой метод расчета цепи Крон представил как преобразования тензоров в пространстве сети, где сопротивление – метрический тензор, а ток и напряжение – контравариантные и ковариантные векторы. Коэффициенты выражения токов в n свободных ветвях i ^α через токи в m контурах связанной сети i ^α ` составят матрицу преобразования <sup>m</sup>C <sup>α</sup>α ` (порядка m x n ):

i

α

^mC^a_a- i " .

Строки матрицы показывают, в какие контуры входит данная ветвь, а столбцы – из каких ветвей состоит контур. Рассеиваемая мощность P равна сумме мощностей на ветвях, т.е. произведений напряжения и тока в каждой свободной ветви: P = ea ia (a = 1..... п). Аналогично для напряжений и токов в контурах связанной сети: P' = ea- ia' (a = 1, .„, m), где предполагается сумма по одинаковым верхним и нижним индексам. Если постулировать, что мощность при изменении соединений не меняется, и подставить (4), то получим закон преобразования для напряжения, ea- ia' = ea ia = ea C"a- ia', откуда:

e a- = e a ^mC ^aa - = ^mC"_a-_t e a ,

где индекс t означает транспонирование матрицы. Чтобы получить формулу преобразования zae, подставим (4) и (5) в закон Ома в матричной форме:

e a = Z ae i ^e = Z ae " C i^e' ,                                      (6)

но для этого надо в (5) сделать обратное преобразование e_a = (ⁿC^a_a-_t)"¹ e_a- . Это возможно когда сеть состоит из одних контуров (m = п) ; в этом случае матрица C ^a _a- квадратная, и может иметь обратную матрицу. В общем случае, когда контуров меньше чем ветвей, это невозможно, поскольку матрица ^mC ^a _a - прямоугольная, для нее не существует обратной матрицы. Однако если формально подставить в (6), то:

ea = (”Caa-t)-* ea- = Zae "C- ■ °',(7)

а затем умножить обе части уравнения на матрицу ( " C ",- ) , то получим:

(”Caa-)t ("C-a-,)-' ea- = ((*C‘a-)t Zae "C",)"' "■ = <",(8)

откуда, используя постулат о том, что вид уравнений поведения не меняется при соединениях [4] ( Крон , 1978), получим формулу преобразования сопротивления:

Za-в' = ("Caa-)t Zae "C -(9)

В (9) нет обратных матриц преобразования, а значит и не надо «обращать» прямоугольные матрицы. Далее расчет производится контурным методом. Если подставить все формулы преобразования в выражение токов в ветвях связанной сети, то получим:

icв = Vv ("C-, . Zae "C",)"' "C",; ea = "Yc ea(10)

Матрица метрического тензора связанной сети, ^mY_c , выражает токи в ветвях связанной сети через заданные источники ЭДС; назовем ее «матрицей решения».

Делая двойственные замены величин, получим формулы расчета цепи узловым методом, при этом матрица C заменяется на ортогональную матрицу А = C '_t . Крон полагал, что матрица А не имеет такого структурного смысла, как матрица С . Оказалось, что матрица А имеет такой же смысл, но как матрица С = А в двойственной цепи (сети).

Обосновать постулат об инварианте мощности пытались физики, например, Б. Гофман, и математики, Дж. Рот. Дискуссия по применению тензоров в технике растянулась на десятки лет, в том числе на страницах журнала «Электричество», и носила острый характер, порой выходя за рамки научной терминологии [5]. Одни применяли тензорный метод в различных областях физики и техники. Другие отвергали его за прямоугольные матрицы, которые не образуют группу. Несмотря на проблемы, «эти работы, несомненно, оказали глубокое влияние на развитие многих областей знания и способствовали прогрессу в разработке методов решения системных задач с помощью цифровых вычислительных машин» [1] ( Веников, 1985). Крон писал, что чем дальше он уходил от электротехники, к сетевым моделям в физике, технике, тем более точно пришлось определять основные понятия в самой электротехнике. Теперь ясно, что это общие законы структуры, которые присущи всем неживым и живым системам, от микромира до космических масштабов.

Таким образом, реально постулат Крона об инварианте мощности не выполняется, поскольку мощность при изменении связей меняется, а вывод формул тензорного анализа сетей содержит недопустимое обращение прямоугольной матрицы. Однако его метод расчета цепей и машин дает правильные результаты. Получается диалектическое противоречие. Автор провел ряд расчетов цепей при изменении структуры, пытаясь найти закономерность изменения мощности. Оказалось, что решение, в согласии с законами диалектики, лежит в другой «плоскости». Рассеиваемая мощность меняется в одной цепи при изменении связей, но постоянна в сумме цепи и цепи с двойственной структурой.

В основе постоянства мощности в физических цепях с двойственной структурой лежат абстрактные, математические свойства структуры связей. Существует фундаментальный закон двойственности структуры. Он выражается инвариантом, который связывает метрические матрицы (матрицы решения) абстрактных двойственных сетей.

В сети двойственными являются замкнутые и разомкнутые пути, воздействия и отклики, внешние и внутренние воздействия, сеть и двойственная к ней сеть (ее величины обозначим подчеркиванием). Если, например, соединить две ветви, то два узла сливаются (уменьшается число узлов). Возникает новый независимый контур, растет размерность подпространства замкнутых путей. При этом исчезает разомкнутый путь, уменьшается размерность базиса разомкнутых путей. Общая размерность пространства путей в сети не меняется, она постоянна и равна количеству элементов - ветвей, т.е. n = m + j.

В двойственных сетях (пример дан на рисунке 1) постоянны размерности подпространств замкнутых и разомкнутых путей. Замкнутому пути в сети соответствует разомкнутый путь в двойственной сети, и наоборот: n = n, m + m = n, j + j = n. Слиянию двух узлов в сети соответствует разделение узла на два в двойственной сети, и наоборот. Таким образом, при изменении структуры двойственных сетей общая размерность подпространств замкнутых путей остается постоянная; общая размерность подпространств разомкнутых путей постоянная. Сумма метрических тензоров постоянна.

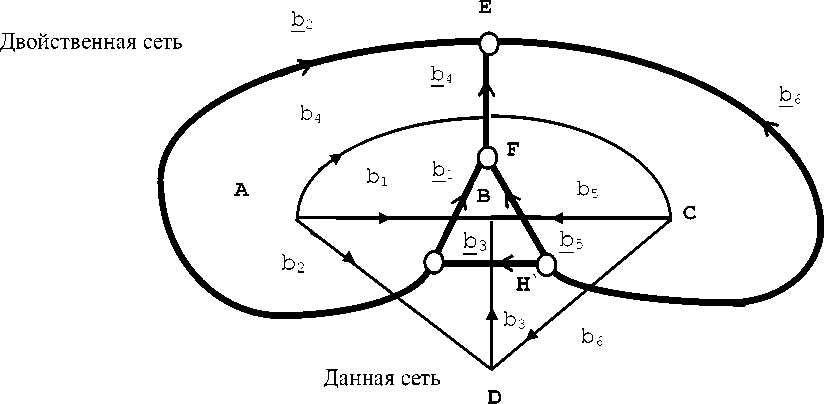
Рис. 1. Пример ориентации ветвей в двойственных сетях из 6 ветвей

Если сопротивления ветвей равны единицам ( Z = Y = I) , то инвариант двойственности связывает матрицу решения сети и матрицу решения двойственной сети:

m C ( m C t ^mC) -1 ^mC_t + j A (A t j A))^{-1 j}A_t = ^mC ( m C t ^mC)^{-1 m}C_t + m C ( m C t ^mQ^{-1 m}C_t = I (11)

В (11) m C = j A - матрица преобразования замкнутых путей сети, или разомкнутых путей двойственной сети, а j A = ^mC - матрица преобразования разомкнутых путей сети, или замкнутых путей двойственной сети, I - единичная матрица. Это закон структуры, не связанный с материей. Сюда входят только матрицы преобразования путей.

Закон структуры проявляется в физических цепях. Если ветви сети имеют веса-сопротивления (собственные и взаимные), с матрицей сопротивлений (метрический тензор) Z ФI , ( Z = Y¹ ), то инвариант двойственных сетей для замкнутых путей примет вид:

m C ( m C t Z^mC)^{-1 m}C_t + Y m C ( m C t Y m C)"^{1 m}C Y= Y = ( Z) ^-1 ,                            (12)

Для разомкнутых путей инвариант имеет двойственный вид, с заменой С на А, Z на Y. Инвариант связывает метрические тензоры (матрицы решения) двойственных сетей (цепей). Компоненты потока энергии расположены в базисе замкнутых (внутреннее воздействие) или разомкнутых (внешнее воздействие) путей. В данном случае инвариант - это постоянство квадрата величины вектора (потока энергии): часть его расположена в сети, часть в двойственной сети, а сумма постоянна для любых соединений.

В двойственных сетях сумма токов в каждой ветви и сумма напряжений на каждой ветви постоянная. Сумма мощностей, рассеиваемых в двойственных сетях постоянная. Сеть и двойственная сеть дополняют друг друга, обладая полнотой единого объекта. По своей сути инвариант двойственности есть проявление закона сохранения потока энергии . Этот закон сохранения, следующий по физической размерности после закона сохранения энергии, является физико-структурным законом. Из него следует существование двойственных структур, расположенных в двойственном пространстве.

Крон был прав в том, что изменение соединений ветвей не меняет мощность источников. Однако мощность, рассеиваемая в цепи от этих источников, делится, «расщепляется» между данной и двойственной структурами. В каждой из цепей мощность меняется при изменении соединений, в том числе, при соединении ветвей в цепь. Поэтому постулат об инвариантности мощности, как сформулировал его Крон, не выполняется.

Расчет сетей при изменении структуры. Изменения структуры меняют метрические свойства сети в соответствии с инвариантом двойственных сетей. Изменения структуры состоят в изменении числа узлов. Разъединение увеличивает число узлов, Δ J > 0, а соединение уменьшает число узлов, Δ J < 0. При этом взаимно меняется число контуров и разомкнутых путей в двойственных сетях. Уменьшение числа узлов увеличивает число замкнутых путей (контуров), уменьшает число разомкнутых путей. Увеличение числа узлов увеличивает число разомкнутых путей, уменьшает число замкнутых путей (контуров).

Это дает две основные формулы расчета сети для наложения связей:

Y²⁺ c = Y¹ c + Δ Y c = Y¹ c + (I – Y¹ c Z) Δ C t [ Δ C Z (I – Y¹ c Z) Δ C t ]^–1 Δ C (I – Z Y¹ c ) , (13)

Zc2+ = Zc1 – ΔZc = Zc1 – Zc1 ΔCt (ΔC Zc1 ΔCt)–1 ΔC Zc1 = Zc1 – Z ΔYc Z(14)

Здесь матрицы изменения решения:

ΔYc = (I – Y1c Z) ΔCt [ΔC Z (I – Y1c Z) ΔCt]–1 ΔC (I – Z Y1c),(15)

ΔZc = Zc1 ΔСt [ΔC Zc1 ΔCt]–1 ΔC Zc1,(16)

где: Y¹ c = ^mC 1t (^mC 1 Z ^mC 1t )^{–1 m}C 1 – матрица решения сети со старой структурой (замкнутые пути, внутренние источники); Z c ¹ = ^jA 1t (^jA 1 Y ^jA 1t )^{–1 j}A 1 – матрица решения сети со старой структурой (разомкнутые пути, внешние источники); Δ C – матрица преобразования путей, которые меняются (замыкаются или размыкаются) при изменении структуры сети.

Варианты расчета двойственных сетей при изменении структуры представлены в таблице. Контуры представляют базис в замкнутой сети, а разомкнутые пути – базис в открытой сети. Возможен расчет сети при уменьшении числа узлов (наложение связей) и при увеличении числа узлов (разрывание связей).

Таблица Расчет двойственных сетей при изменении структуры

Двойственность изменяемых путей Δ m = Δ j = Δ m = Δ j
Данная сеть		Двойственная сеть
Уменьшение числа узлов		Увеличение числа узлов
m – контуры j – разомкнутые пути	Y 2+c = Y 1c + Δ Y c Z c2+ = Z c1 – Δ Z c	j – разомкнутые пути m – контуры	Y 2–c = Y 1c – Δ Z c Z c2– = Z c1 + Δ Y c
Увеличение числа узлов		Уменьшение числа узлов
m – контуры j – разомкнутые пути	Y 2–c = Y 1c – Δ Z c Z c2– = Z c1 + Δ Y c	j – разомкнутые пути m – контуры	Y 2+c = Y 1c + Δ Y c Z c2+ = Z c1 – Δ Z c

В таблице представлена обобщенная диакоптика (метод расчета по частям), где, в отличие от известной работы Крона [3], даны все виды расчета при изменении структуры, а не только разделение на части «пуассоновского» и «диффузионного» типов. Алгоритмы расчета процессов при изменении структуры сетей и сетевых моделей сложных систем основаны на инварианте двойственности, и могут применяться для решения задач электротехники. Например, для определения влияния отключения подсистем в электрических сетях в результате аварий или катастроф, или подключения подсистем, при введении новых мощностей, и т.д.

Поток энергии, численно равный мощности, рассеиваемой в сети, можно наглядно представить круговой диаграммой как красно-синий «мячик», до половины погруженный в «воду». Двойственная сеть располагается в двойственном, «параллельном» пространстве.

Площадь темной (красной) половины такого мячика соответствует мощности (или квадрату величины вектора) в замкнутых путях данной и двойственной сети, а площадь светлой (синей) половины – мощности в разомкнутых путях. При изменении структуры мощность в двойственных цепях меняется, что отражает изменение площадей разных цветов при вращении двухцветного мячика, в «воде», где:

• •    «воздушная» среда представляет наблюдаемое пространство,

• •    «водная» среда представляет двойственное пространство.

Вращение «мячика» наглядно представляет изменения мощности при изменении структуры, меняя доли красного и синего цвета над (и под) поверхностью раздела двух сред. Сумма площади красного цвета (мощность внутренних источников, т.е. источников напряжения, ЭДС) над и под поверхностью (в данной и двойственной цепи) постоянна.

Сумма площади синего цвета (мощность внешних источников, т.е. тока) над и под поверхностью постоянна. Сумма площади красного и синего цвета над поверхностью, а также сумма площади красного и синего цвета под поверхностью, постоянны. При изменении структуры рассеиваемая мощность меняется, но согласованно, так, что остаются постоянными четыре суммы в базисах замкнутых путей и разомкнутых путей.

Постоянство суммарной рассеиваемой мощности при изменении структуры двух двойственных цепей представляет закон сохранения потока энергии. Полная диаграмма изменения мощности при изменении структуры данной и двойственной сетей, в которых заданы источники энергии двух типов, представлена на рисунке 2.

Фундаментальное значение инварианта постоянства мощности в том, что он показывает: распространение потока энергии в любых структурах (не только электрических, но и других технических, экономических, биологических) с необходимостью сопровождается потоком в двойственной структуре. Можно предположить, что такая структура расположена в ненаблюдаемом в настоящее время двойственном пространстве. Двойственные пространства в совокупности составляют единое пространство с не менее чем удвоенным числом измерений.

Двойственное пространство располагается везде, и должно контактировать с объектами в наблюдаемом пространстве, при распространении потоков энергии, проявляя себя при изменении структуры систем, по которым энергия распространяется. Это расширяет представление о физическом мире. К осознанию фундаментальной роли структурных связей движется физика, где предлагаются теория струн и другие гипотезы многомерного мира, параллельных пространств и других Вселенных. Постоянство потока энергии в двойственных структурах электрических цепях дополняет теорию об электромагнитной Вселенной И.П. Копылова.

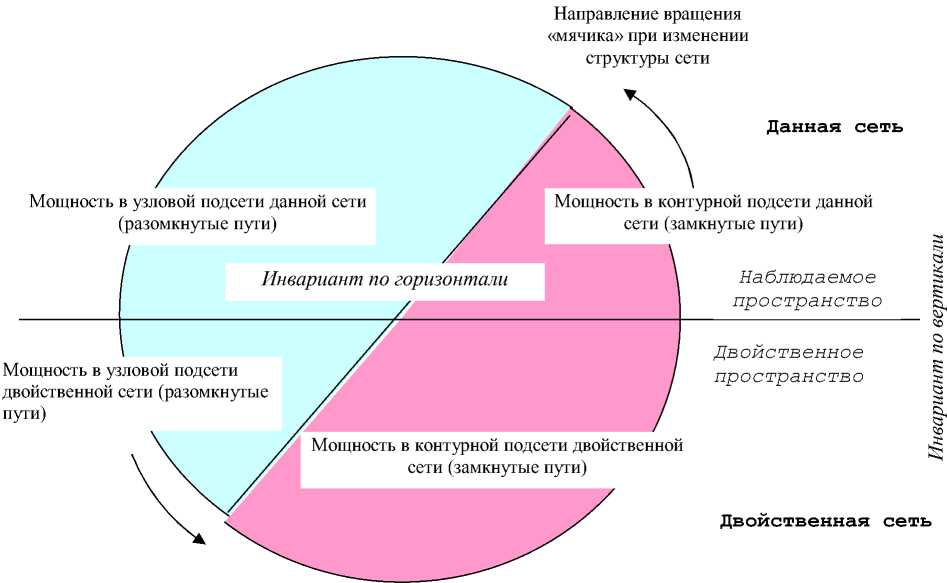
Рис. 2. Диаграмма изменения мощности в двойственных цепях при изменении структуры

В 40–70-тые годы Крон использовал эквивалентные электрические цепи в качестве эталонной системы для моделирования физических, технических и экономических систем, используя аналогии процессов и структуры. Были построены модели в виде эквивалентных электрических цепей для уравнений поля Максвелла (1944), Шредингера (1945), Навье-Стокса, модели упругих систем (строительные конструкции, разрезные диафрагмы турбин), модели электронных ламп, электрических машин, сетей передачи электроэнергии, ядерного реактора, транспортной задачи и другие [3]. Эти модели применялись для расчета сложных систем по частям. Теперь для моделирования можно применять аппарат двойственных сетей.

Представляют интерес работы Крона по многомерным (полиэдральным) сетям. Полиэдральные сети в работах 1958-1968 гг., состоят не только из одномерных ветвей, но также из плоскостей, точек, объемов, многомерных элементов и проводят не только электрический ток, но и потоки энергии других видов. Например, магнитные и диэлектрические силовые линии определяются через поверхностные интегралы по плоскостям графа, ограниченным контурами. Магнитный поток распространяется через двумерные поверхности (представленные обмотками в электрических машинах). Электромеханические преобразователи (электрические машины) являются простейшим примером полиэдральных сетей, в данном случае двумерных сетей.

Процессы наука изучает давно, однако свойства структуры до сих пор изучены недостаточно. Существенную роль структуры играют в экономике. Известно, что наибольший вклад в падение производства после гражданской войны внесло разрушение хозяйственных связей. После распада СССР на 15 независимых частей также была нарушена структура хозяйственных связей при сохранении природного, промышленного, человеческого потенциала. В результате, по данным ЦЭК при Правительстве РФ, индекс интенсивности промышленного производства со 100% в январе 1990 г. снизился до 38% в августе 1998 года, т.е. в 2,5 раза.

Для анализа влияния структуры связей на производство автор разработал сетевую модель межотраслевого баланса, используя аналогии с электрической цепью [5, 6]. По физическому смыслу модель применима для анализа хозяйственных связей на уровне предприятий, отраслей, регионов, государств, и обеспечивает расчет производства продуктов и потребления ресурсов для вариантов управления развитием, структурных реформ, последствий разделения экономической системы на части или создании союзов, и т.д.

Токи представляют потоки продуктов, а напряжения моделируют финансовые воздействия (потоки денежных средств). Это первая сетевая модель, когда живая (экономическая) система представлена неживой (технической) системой за счет применения тензорных величин, связи процессов и структуры, инвариантов двойственности.

Отрасли (производства) выпускают продукты для удовлетворения спроса (плана) и межотраслевых поставок; потребляют ресурсы и продукцию друг друга. Задача состоит в расчете объема производства (валового выпуска) отраслей и ресурсов, обеспечивающих спрос и поставки. Это определяет система уравнений:

X а = £ Х ав + У а .      Х а = Z Х а» + У а .             (17)

а = 1

где валовые выпуски отраслей X ^α ( α = 1,..., n ) обеспечивают план y α и поставки x αβ . Межотраслевые поставки задают коэффициенты прямых затрат a ^αβ (количество продукта одной отрасли для производства единицы продукта другой отрасли): x αβ = a αβ X β . Потребление ресурсов определяют коэффициенты b _Y » , - количество ресурса у для производства единицы продукта отрасли β : r γβ = b γβ X β .

Решение сводится к обращению экономической матрицы Леонтьева, (I – A). Для реальных задач порядок этой матрицы может составлять тысячи строк и столбцов, в итоге время решения превышает период планирования. Это затрудняет управление экономикой.

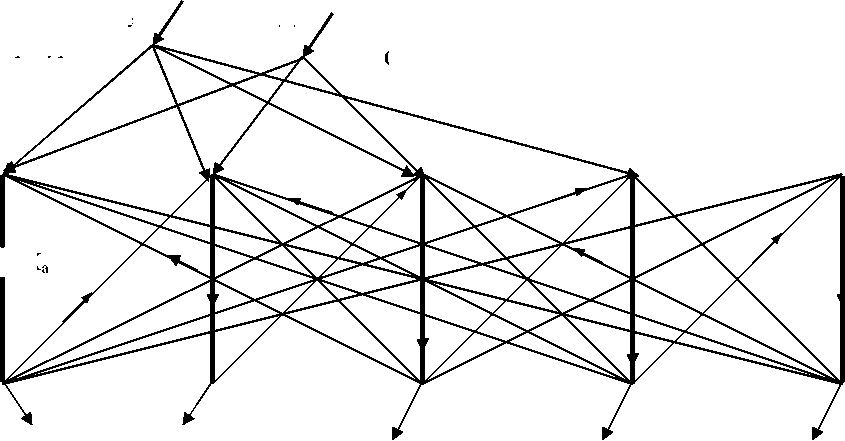
Сетевая модель межотраслевого баланса включает все соотношения между потоками в системе. Уравнения системы приводятся к тензорному виду, т.е. при изменении координат (структуры спроса, хозяйственных связей), все величины преобразуются линейно. На рисунке 3 показан пример пяти отраслей, связанных поставками (наклонные линии), сверху поступают ресурсы, стрелки внизу показывают спроса (план).

ПРИРОДА

Сырьевые ресурсы

Энергетические ресурсы

X

Xb

Розничная торговля

Сельское хозяйство

Промышленность

Строитель-     Транспорт ство

Спрос (план) на произведенные продукты

Рис. 3. Структура сети потоков продуктов в отраслях

Модель открытая, в том смысле, что любую отрасль можно перевести в разряд ресурсов (и наоборот). Можно добавить или исключить отрасли; соответственно изменится состав поставок и потребление ресурсов. Например, для расчета агрегированной модели региона можно ввести отрасль «прочие производства», и сохранить полноту модели.

Связь потоков продуктов в (17) записана как закон сохранения потоков в узлах на выходе отраслей, аналогично первому закону Кирхгофа. Формулы для коэффициентов прямых затрат и ресурсов аналогичны законам Ома. На рисунке 3 можно видеть, что также есть связь потоков в узлах входов отраслей:

X ^α = Σ x ^αβ + Σ r ^γβ = Σ a ^αβ X β + Σ b ^αβ X β = ( Σ a ^αβ + Σ b ^αβ ) X β .            (18)

Потребление ресурсов r ^γβ и поставок x ^αβ определяется, следовательно, величиной валового выпуска X α . В (18) слева и справа стоит численно один и тот же вектор, поэтому:

Σ a ^αβ + Σ b ^αβ = 1 .                                        (19)

Физически это означает: для выпуска продукта нужны все необходимые поставки и ресурсы – условие очевидное, а потому обычно не используемое. Однако это обеспечивает полноту описания потоков в сети и позволяет привести уравнения к тензорному виду.

Если в каждой отрасли выпуск на выходе X ^α равен выпуску на входе X α , то система отраслей работает в стационарном режиме. То есть потоки финишного продукта, поставок, ресурсов определены и постоянны. Тогда метрический тензор единичный, g ^βα = δ ^βα = 1 , что в геометрии соответствует декартовым координатам.

Когда происходят изменения структуры связей, спроса, ресурсных возможностей, и т.д., то система отраслей работает в переходном режиме, и тогда X β ≠ X ^α . Тогда метрический тензор усложняется, а системы координат становятся криволинейными. За счет искривления пространства система настраивается на стационарный режим. На каждом этапе вычислений X β ^m ≠ X ^α m . Это выражает степенной ряд обращения матрицы Леонтьева:

X β = δ βα y ^α + a βα y ^α + (a βα y ^α )² + (a βα y ^α )³ + ... = X ^β 0 + X ^β 1 + X ^β 2 + X ^β 3 +...

Если первоначально предприятия стоят, а затем начинается выпуск продуктов в объеме спроса, то: X α 0 = δ αα y ^α = y ^α . Для этого нужны поставки в количестве x ^βα 0 = a ^βα X β 0 = a ^βα y ^α . Тогда выпуск продукта возрастет до:

X ^β 1 = y ^α + a ^βα y ^α = ( δ ^βα + a ^βα ) y ^α .                       (20)

При вычислении (m + 1) члена ряда X ^β (m+1) на выходе отрасли уже возрастет до величины:

X ^β (m+1) = X ^β m + (a ^βα )^(m+1) y ^α ,                                (21)

где матрица a ^βα возводится в степень (m + 1) , а поток продукта на входе, X β m = a ^βα X ^β m , еще прежний (следующий член ряда еще не вычислен). Записывая X β m через сумму предыдущих m членов ряда, выразим последующий член ряда X ^β (m+1) через предыдущий X ^β m :

/ ^ав m m + 1

х а + , = ( +         )-----) X в m                    (22)

Z ( a * ) p p = 0

В скобках – метрический тензор g ^βα ; он связывает ковариантные и контравариантные компоненты вектора потока продуктов в отраслях – ветвях данной сети. Поскольку a ^βα < 1 , то при стремлении числа членов ряда m к бесконечности дробное выражение стремится к нулю и тогда g ^βα = δ ^βα . Итак, на каждом шаге вычислений g ^βα переходит от сложной кривизны, к нулевой кривизне декартова пространства.

В (22) отличны от нуля те компоненты тензора gβα, которые соответствуют поставкам, связывающим отрасли, т.е. aβα ≠ 0. Они заданы структурой хозяйства. Их отличие от нуля показывает, что процесс установления потоков продуктов происходит в пространстве с кривизной.  В  [8]  показано  (Kron,  1934),  что  подобные  геометрические  аналогии соответствуют переходным процессам в электрических машинах. Изменение кривизны показывает переходные процессы, в частности, при изменении структуры связей, разделении на независимые подсистемы, при внедрении инноваций.

Соответствие между продуктами и сетью обеспечивают двойственные источники в замкнутых путях; для этого введены источники ЭДС в ветвях поставок. Величина источников напряжения определяется итерациями при переходе к связанным отраслям, которые обмениваются своими продуктами. Применение двойственности позволяет представить процессы в живой системе экономики комбинацией двойственных величин в сети – неживой электрической цепи. Двойственные отклики замкнутых и разомкнутых путей в совокупности представляют сумму компонент – потоков продуктов в отраслях:

ЧёР       ч = p " i

X " = 1 П + S i^ = S ( а «в ) ⁴ У ^в = У " + а «в У ^в + ( a =e ) 2 У ^в + ■■■ + ( a =e ) p - У ^{в , (23)}

4 =1

поставок между отраслями:

ч = p

X * p = Im +S im, = (a„, ) p-1 y e

4 = 1

ресурсов, потребляемых отраслями:

,=p                      , =p-i rp" = im + X im, = ь „ ( у ° +X (a„,)" у e)

, =1

Эти суммы независимых, двойственных контурных и узловых токов, численно равны потокам продуктов в отраслях, поставках и ресурсах, получаемым при вычислении p членов степенного ряда (при обращении экономической матрицы). Для расчета по частям сетевая модель делится на подсистемы, решения которых затем алгоритмически соединяют в решение всей системы. Показано, что такой алгоритм обеспечивает многократное снижение объема вычислений, ускоряя плановые расчеты [5, 6].

Именно для этих целей модель первоначально и разрабатывалась. Однако сетевая модель генерирует также ковариантные компоненты вектора потока энергии (напряжения на ветвях сети). Они представляют пропорции денежных средств (например, оборотные средства), которые должны распределяться в системе производства для обеспечения заданного выпуска. Пропорции, поскольку денежные потоки измеряются с точностью до стоимости денежной единицы (в энергетическом эквиваленте), точно так, как потенциал измеряется не абсолютно, а относительно нулевого узла (заземления).

В каждой ветви этой сетевой модели представлены как воздействия (источники тока и напряжения), так и отклики (напряжения и токи). Потоки продуктов представлены только токами (отклики на источники двух видов). Напряжения (ковариантные компоненты вектора) не используются. В классической задаче баланса нет величин, которым соответствуют напряжения. Таким образом, сетевая модель сама генерирует величины, которые дают новое знание о системе. Это дает подход к решению задачи объединенного материально-финансового баланса, которая не решена и в настоящее время.

Для моделирования инновационной экономики, когда постоянно происходит структурная перестройка, возникают новые отрасли, в условиях изменения структуры цен, нужно развитие этой модели. Такая модель должна отражать изменения в потоках продуктов при изменении цен, а также изменения в ценах при изменении потоков продуктов; обеспечить расчет состояния и перспектив таких изменений. Например, влияние снижения производства нефти на динамику мировых цен, или снижение цен на компьютеры в условиях насыщения рынка. Или изменение стоимости в долларах: нефти, золота, серебра, евро, иены – при уменьшении стоимости валюты США, что наблюдается в последние годы.

В этой связи возникает вопрос о существе метрических характеристик в экономической системе. Их роль могут играть не только коэффициенты прямых затрат, которые устанавливают меру отношений между отраслями. Это могут быть также энергетические эквиваленты между спросом и производством, предложением. В сети денежных потоков, которая является двойственной сетью по отношению к сети продуктов, роль метрики играют ставки процентов за привлечение и размещение денежных средств.

Данная модель обеспечивает расчеты вариантов развития производственнофинансовых систем в интересах управления устойчивым развитием. Для современной экономики, с рынками капитала, многократно превосходящими выпуск реального продукта, необходима модель более высокого уровня. Математический метод, который связывает изменения физических величин – это уравнения Максвелла. Они были получены на основе сетевой модели, которая сложилась в результате анализа опытов Фарадея. В работе Максвелла «О физических силовых линиях», опубликованной в 1861 году приводится наглядная картина электромагнитных процессов, которая представлена здесь на рисунке 4

слева.

Электронное научное издание «Устойчивое инновационное развитие: проектирование и управление»

Промышленность

Торговля

Добыча природных ресурсов

Банки

Ток

Население

Ток

«Вихри» магнитного потока

Рис. 4. Аналогии сетевой модели электромагнитного поля Максвелла (слева) и сетевой модели товарно-денежного оборота в экономике (справа)

Слева маленькие кружки представляют поток электрического тока, который поступает в среду и покидает ее по направлению стрелок. Воздействием является электродвижущая сила, изменение которой приводит в движение потоки энергии. Шестиугольники представляют вихри (магнитного потока), которые постепенно передают энергию вращения соседним вихрям. А те, своим вращением, заставляют двигаться другие носители электрического тока. При снятии нагрузки вихри своей инерцией поддерживают ток, сопротивляясь его мгновенному затуханию.

Если воздействием является изменение (возрастание или убывание) магнитного поля, то откликом является поток электрической энергии, ток. Переходный процесс постепенно распространяется в среде. При снятии нагрузки ток, в виде движения зарядов, поддерживает магнитное поле, сопротивляется его мгновенному затуханию.

Потоки денежных средств обозначены шестиугольниками, пунктиром. Этот процесс показан схематично на рис. 4 справа, где кружки представляют движение продуктов между хозяйствующими субъектами, а шестиугольники представляют оборот кредитно-денежных средств через расчетные, депозитные или кредитные счета в банках.

Исследования по сетевому моделированию экономических систем проведены при поддержке РФФИ, проект 07-06-00209.