Теории пластичности при сложном нагружении по плоским траекториям деформаций

ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2021PNRPU MECHANICS BULLETIN

Развитие теории пластичности и разработка определяющих уравнений описания процессов сложного нагружения идет двумя основными направлениями. К первому направлению относятся различные варианты [1–12] теории упругопластических процессов, базирующиеся на общей математической теории пластичности А.А. Ильюшина [1]. Ко второму направлению относятся различные варианты [13–41] теории пластического течения при комбинированном упрочнении, базирующиеся на концепции микронапряжений, выдвинутой В.В. Новожиловым [16, 19].

В практических расчетах конструкций широкое применение в настоящее время нашли варианты теории пластического течения при комбинированном упрочнении. Они имеют обобщение на неизотермические процессы нагружения, а также процессы накопления повреждений, т.е. позволяют определять ресурс.

Практически ни в одной работе, предлагающей вариант теории, не приводится сравнение с уже имеющимися вариантами и не определяются преимущества того или иного варианта. В настоящей работе предлагается провести сравнительный анализ вариантов теории пластического течения при комбинированном упрочнении, наиболее применяемых в программных комплексах расчета конструкций. Для начала будут рассматриваться процессы сложного нагружения по плоским траекто- риям деформаций, охватывая весь спектр траекторий от многозвенных ломаных до криволинейных траекторий постоянной и переменной кривизны как средней, так и большой кривизны. Анализ результатов исследований проводится в векторном пространстве А.А. Ильюшина [1, 2].

Рассматриваются варианты теории: модель изотропного упрочнения, модель Ишлинского–Прагера– Кадашевича–Новожилова [13–16] (линейное кинематическое упрочнение + изотропное упрочнение); модель Оно–Ванга [33, 34]; модель Армстронга–Фредерика– Кадашевича [17, 20] (на основе этой модели строится модель Коротких); модель Шабоша [23–25] с тремя эволюционными уравнениями Армстронга–Фредерика– Кадашевича; модель Темиса [35], построенная на основе инвариантной теории пластичности [32]; модель Бондаря [26–31] с трехчленной структурой эволюционного уравнения для кинематического упрочнения.

Получены и приводятся материальные параметры (функции), замыкающие каждый вариант теории пластичности. Исследования процессов сложного нагружения проводятся по плоским траекториям деформаций в виде квадрата, трех окружностей разного радиуса, проходящих через начало координат, а также траектории в виде астроиды. Результаты расчетов сопоставляются с результатами экспериментальных исследований [7–9] тверской научной школы под руководством В.Г. Зубчанинова. Сопоставление результатов расчетов по различным вариантам теории и экспериментов проводится по ответным траекториям напряжений, скалярным и векторным свойствам. В следующих работах предполагается рассмотреть сложные процессы нагружения по пространственным траекториям деформаций, а также процессы нагружения по траекториям напряжений.

1. Варианты теории пластичности

Для определения скоростей пластической деформации используется ассоциированный с уравнением (3) градиентальный закон течения:

°

p =^ f Х= 3

9а«   2

*

^i L₆ P

* ° u * .

° u

Рассматриваются конструкционные стали, однородные и начально изотропные. В процессе упругопластического деформирования в материале может возникать только пластическая деформационная анизотропия. Рассматриваются малые деформации при температурах, когда нет фазовых превращений, и скоростях деформаций, когда динамическими и реологическими эффектами можно пренебречь.

Рассматриваются наиболее применяемые в практических расчетах варианты теории пластического течения при изотропном, кинематическом (анизотропном) и комбинированном (изотропном и кинематическом) упрочнениях.

Для всех вариантов теорий тензор скоростей деформации °_у представляется в виде суммы тензоров скоростей упругой ° e и пластической ° p деформаций:

° ^ = ° j + ° Р. (1)

Упругие деформации при изменении напряжений следуют обобщенному закону Гука:

° « = 1 [^ « ^{-v ( 3} ° о ⁵ «- ^ « ) ] , (2)

жений;

p

° u *

где E, v - соответственно модуль Юнга и коэффициент

Пуассона; с у - тензор напряжений; а₀ = 1 и.. - среднее

напряжение.

Для всех рассматриваемых вариантов теорий принимается поверхность напряжения, разделяющая области упругого и упругопластического состояний. Поверхность нагружения изотропно расширяется или сужается и смещается в процессе нагружения. Уравнение поверхности нагружения принимается в следующем виде:

f Ы= 3 ⁽ s j ^- a y ⁾⁽ s j ^{- a} «)^- C = 0.       ⁽³⁾

Здесь s _z* = s_y - a.. - девиатор активных [15] напряжений; s – девиатор напряжений; a – девиатор микронапряжений (добавочных напряжений, остаточных микронапряжений [16, 18, 19]) характеризует смещение поверхности нагружения, т.е. направленное (анизотропное) упрочнение. Скаляр C_p ( ° p ) , зависящий от накопленной пластической деформации, отвечает размеру (радиусу) поверхности нагружения и характеризует изотропное упрочнение.

ij

. f 3 . . *             *   *

Здесь G „ =1 - S j S j

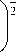
– интенсивность активных напря-

² ° ^p ° p I

3 ij j J

– скорость накопленной пла-

стической деформации.

Для всех рассматриваемых вариантов теории изо-

тропное упрочнение определяется зависимостью радиуса поверхности нагружения от накопленной пластической деформации:

C p = C p ( ° p * ) .

Следует отметить, что для каждого варианта зависимость (5) определяется функцией, соответствующей рассматриваемому варианту.

Рассматриваемые варианты отличаются только эволюционными уравнениями для смещения центра поверхности нагружения. Ниже приводятся эволюционные уравнения для каждого варианта и соответствующие материальные функции конструкционных сталей 9Х2 и 40Х16Н9Г2С, на образцах из которых проводились испытания на сложное нагружение.

Материальные функции для всех представленных моделей определялись с использованием участка диаграммы статического растяжения до деформации 0,1 и диаграммы растяжения после предварительного сжатия до деформации 0,02.

Модель изотропного упрочнения ay = 0.                        (6)

Данную модель замыкают следующие материальные параметры (функции):

E , v , C p ( ° p * ) .                      (7)

Материальные функции конструкционной стали 40Х16Н9Г2С (табл. 1)

E = 2-10 5 МПа,  v = 0,3.

Таблица 1

Функция изотропного упрочнения.

Ст. 40Х16Н9Г2С

Table 1

Isotropic hardening function. St. 40Х16Н9Г2С

p ° и *	0	0,00016	0,00061	0,0011	0,0021	0,0048	0,0071	0,01	0,1
C p , МПa	62	144	204	228	256	295	335	350	800

Материальные функции конструкционной стали 9Х2 (табл. 2)

E = 2.3-10 5 МПа,  v = 0,3.

Таблица 2

Функция изотропного упрочнения. Ст. 9Х2

Table 2

Isotropic hardening function. St. 9Х2

p e и * .	0	0,00025	0,00075	0,0015	0,002	0,0055	0,0079	0,01	0,1
C , МПa	209	240	270	300	310	370	395	440	940

Модель    Ишлинского–Прагера–Кадашевича–

Новожилова [13–16]

a j = з g e P .                      (8)

Данную модель замыкают следующие материальные параметры (функции):

E , v , g , C_p ( e p * ) .                     (9)

Материальные функции конструкционной стали 40Х16Н9Г2С (табл. 3)

E = 2 -10 5 МПа,  v = 0,3, g = 3350 МПа.

Таблица 3

Функции изотропного упрочнения.

Ст. 40Х16Н9Г2С

Table 3

Isotropic hardening function. St. 40Х16Н9Г2С

p e ll *	0	0,00023	0,0004	0,0008	0,0025	0,008	0,01	0,024	0,086
C , МПa	63	151	173	208	247	287	297	324	414

Материальные функции конструкционной стали 9Х2 (табл. 4)

E = 2.3-10 5 МПа,  v = 0 , 3 , g = 5000МПа.

Таблица 4

Функция изотропного упрочнения. Ст. 9Х2

Table 4

Isotropic hardening function. St. 9Х2

p e u *	0	0,0003	0,0006	0,0013	0,0026	0,0055	0,0084	0,018	0,21
C , МПa	209	241	263	282	299	345	357	408	468

Модель Оно–Ванга [33, 34]

M a   X aj), aj ) = 2 g(m) ep,(10)

m=1

f p ^m ) o <^m ) ;

0mmm

, если a ' ⁷ > o ' ) П а ' ) s „ >  0;

u    a   jj

^{( m} ) I 3   ^{( m} )

a u     v 2 a ^zj

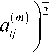
Данную модель замыкают следующие материальные параметры (функции):

E , v, P ^{( l )} , o*,..., p ^{( M} ) , o <^M ) , C p ( e p . ) .        (12)

Здесь в расчетах принимается M = 10 .

Материальные функции конструкционной стали 40Х16Н9Г2С (табл. 5)

E = 2-10 5 МПa,  v = 0,3;

в^{( 1 )} = 10000, p^{( 2 )} = 3400, в^{( 3 )} = 2000, p * ^{4 )} = 1400, в^{( 5 )} = 1050;

в^{( 6 )} = 700, в^{( 7 )} = 450, в^{( 8 )} = 2801, в^{( 9 )} = 161, в^{( 10 )} = 90;

Q¹ = 1,5 МПa, Q^{2 )} = 5МПa, о (, ^{3 )} = 7,5МПa,o<^{4 )} = 9МПa;

Q⁵ ) = 15МПa, Q * ⁶ ) = 26МПa, ct⁽J ) = 33,5МПa;

о ( 8 ) = 29 МПa, q ⁽9 ¹ = 11,5 МПa, q' P" = 41 МПз.

Таблица 5

Функции изотропного упрочнения.

Ст. 40Х16Н9Г2С

Table 5

Isotropic hardening function. St. 40Х16Н9Г2С

p e u *	0	0,0002	0,0004	0,008	0,0025	0,008	0,01	0,024	0,086
C , МПa	62	125	131	137	124	147	157	224	534

Материальные функции конструкционной стали 9Х2 (табл. 6)

E = 2,3-10⁵ МПa,   v = 0,3;

в^{( 1 )} = 8870,   в^{( 2 )} = 1811, в^{( 3 )} = 985, p^{( 4 )} = 666,   p^{( 5 )} = 499,

P^{( 6 )}= 358,   p * ^{7 )}= 240,   p^{( 8 )}= 142,   p^{( 9 )} = 114,   p^{( 10 )} = 82;

0* 1 ) = 1,2 МПa, o*^{2 )} = 8МПa, o * ^{3 )} = 12МПa, q< ^{4 )} = 15 МПa, o*^{5 )} = 19МПa, o * ^{6 )} = 28МПц, o *, ⁷ ) = 36МПa, o ' / ) = 24МПa, o * ⁹ ) = 8МПa, o * ¹⁰ ) = 87МПa.

Таблица 6

Функция изотропного упрочнения. Ст. 9Х2

Table 6

Isotropic hardening function. St. 9Х2

p e u *	0	0,0003	0,0006	0,0013	0,0026	0,0055	0,0084	0,018	0,21
C p , МПa	209	229	233	232	211	187	188	255	1120

Модель Армстронга–Фредерика–Кадашевича [17, 20]

a ij = gg ^e p + g a^a,j S U . .                ⁽¹³⁾

Данную модель замыкают следующие материальные параметры (функции):

E , v , g , g a , C p ( e p . ) .                 (14)

Следует отметить, что эволюционное уравнение (13) используется в модели Коротких [21], ниже приведены материальные функции, полученные для модели Коротких [21, 22].

Материальные функции конструкционной стали 40Х16Н9Г2С (табл. 7)

E = 2-10 5 МПа,  v = 0,3, g = 38250 МПа, g„ =-300.

Таблица 7

Функции изотропного упрочнения.

Ст. 40Х16Н9Г2С

Table 7

Isotropic hardening function. St. 40Х16Н9Г2С

p e u *	0	0,0002	0,0004	0,0008	0,0025	0,008	0,01	0,024	0,086
C , МПa	64	143	160	185	190	201	213	281	586

Материальные функции конструкционной стали 9Х2 (табл. 8)

E = 2.3-10⁵МПа,  v = 0,3, g = 33750 МПа, g„ =-250.

Таблица 8

Функция изотропного упрочнения. Ст. 9Х2

Table 8

Isotropic hardening function. St. 9Х2

p e u * .	0	0,0003	0,0006	0,0013	0,0026	0,0055	0,0084	0,018	0,21
C , МПa	209	235	239	252	253	261	305	356	1300

Модель Шабоша [23–25]

m  2mmm aj - gg) <+ + ga W;

M ay = £ aj).

m = 1

Здесь будет использоваться модель, состоящая из трех эволюционных уравнений, т.е. M = 3 . Данную модель замыкают следующие материальные параметры (функции):

^E , ^v , g ^{( 1 )} , g ^{( 2 )} , g ^{( 3 )} ,

, g a ^{2 )} , g^ , C p ( e *. ) .                 (⁷⁾

Материальные функции конструкционной стали 40Х16Н9Г2С (табл. 9)

E = 2 - 10⁵ МПa,   v = 0,3;

g ^{( 1 )} = 16150 МПa, g ( 1 ) = - 147, g ^{( 2 )} = 126300 МПa;

g < ^{2 )} =- 1570, g ^{( 3 )} = 768650 МПa, g ( ^{3 )} =- 14730.

Таблица 9

Функции изотропного упрочнения.

Ст. 40Х16Н9Г2С

Table 9

Isotropic hardening function. St. 40Х16Н9Г2С

p e u *	0	0,0002	0,0004	0,0008	0,0025	0,008	0,01	0,024	0,086
C p , МПa	91	91,5	92	93	95	112	122	166	477

Материальные функции конструкционной стали 9Х2 (табл. 10)

E = 2,3 - 10⁵ МПa, v = 0,3;

g ^{( 1 )} = 9200 МПa, g ( 1 ) = - 10,   g ^{( 2 )} = 63 960МПa;

g < ² ) = - 1000, g <³⁾ = 14130МПa, g *^{3 )} = - 100 000.

Таблица 10

Функция изотропного упрочнения. Ст. 9Х2

Table 10

Isotropic hardening function. St. 9Х2

p e u *	0	0,0003	0,0006	0,0013	0,0026	0,0055	0,0084	0,018	0,21
C , МПa	209	228	227	237	240	259	285	266	301

Модель Бондаря [26–31]

2    .2

aij = -g eP +^-g6sp + gaaij jep.;(18)

g = ^E a +P" a , g e = ^E a P , g a = -P-

Данную модель замыкают следующие материальные параметры (функции):

E, v, Ea, a a, p, Cp (ep.).(19)

Материальные функции конструкционной стали 40Х16Н9Г2С (табл. 11)

E = 2 - 10⁵ МПа,   v = 0,3,

E_a = 3550МПa , o_a = 140МПa, в = 445.

Материальные функции конструкционной стали 9Х2 (табл. 12)

E = 2,3 - 10⁵ МПa, v = 0,3;

E„ = 4770 МПa, a_a = 160МПa, в = 265.

Таблица 11

Функции изотропного упрочнения.

Ст. 40Х16Н9Г2С

Э = ^

I ^э '|

Э

Э з

Э 4

Table 11

Isotropic hardening function. St. 40Х16Н9Г2С

p е и *	0	0,0002	0,0004	0,0008	0,0025	0,008	0,01	0,024	0,086
C , МПa	64	137	150	166	153	151	159	190	274

IЭ5 J

³ ₂ ^e 11

^ (e22 + eH/2)

2 e ₁₂

2 e ₁₃

2 e 14

eij = еij -5ij ео, е0 = ^£п ,

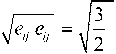
Длина дуги траектории деформаций определяется

выражением

Таблица 12

Функция изотропного упрочнения. Ст. 9Х2

⁵ ч Э dt = J ⁽ e j e j ) ² dt ,

Table 12

Isotropic hardening function. St. 9Х2

p е и *	0	0,0003	0,0006	0,0013	0,0026	0,0055	0,0084	0,018	0,021
C p , МПa	227	246	249	248	230	220	230	246	320

Модель Темиса [32, 35]

aj = a, (еP*H + a2 (=*;(20)

Ij = K(ou,ep.)ep .(21)

Данную модель замыкают следующие материальные функции:

• E, v, a, (sp.) , a2 (sp*), K(o„,ep*), Cp (ep*).(22)

• 2.    Векторное представление напряжений и деформаций

Материальные функции конструкционных сталей 40Х16Н9Г2С и 9Х2 приведены в работе [35, 42], расчеты по модели Темиса проводились А.Д. Худяковой [42].

Для проверки полученных материальных параметров (функций) сталей 9Х2 и 40Х16Н9Г2С были проведены расчеты одноосного растяжения до деформации 10 % для всех вариантов теории и сопоставлены с результатами экспериментов [9]. Получено надежное соответствие расчетов и экспериментов.

Для удобства сопоставления расчетных и экспериментальных результатов рассматривается векторное представление процессов нагружения и деформирования [1, 2]. Компоненты векторов напряжений S и деформаций Э связаны с компонентами тензоров напряжений o_y и деформаций e_v формулами [1, 2]

I у 1 л- 1 5 . = о„ - 5„ on, S = . S2г Sз S4 > = < V2 ( 522 + 511 /2 ) ^ 5,2 22 51 з .     22 5,4 *, j  jj 1 О0 =-°И , 2 (23) . S5 , S = SlJ 5j = ^з  0 и =o; где Э – вектор скоростей деформаций; e – девиатор скоростей деформаций.Векторные и скалярные свойства являются основными характеристиками, изучаемыми при экспериментально-теоретических исследованиях процессов упругопластического деформирования материалов при сложном нагружении. В качестве векторных свойств при сложном нагружении по плоским траекториям деформаций рассматривается отклонение вектора напряжений от касательной к траектории деформаций. Характеристика ориентации определяется углом сближения 9,

(S ■ Э)

9 = arccos -— vry

SЭ

В качестве скалярных свойств рассматривается изменение модуля вектора напряжений по длине дуги траектории деформаций:

О = o(5) .

• 3.    Многозвенная ломаная траектория деформаций

Сравнение вариантов теории проводится на многозвенной ломаной траектории деформаций в виде квадрата (рис. 1) со стороной 0,01 на плоскости ( Э , Э ₃) вектора деформаций Э .

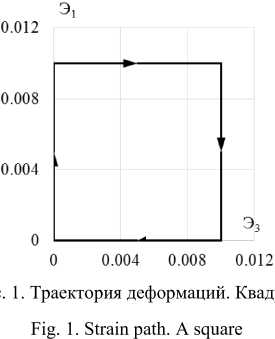
Исследования проводятся на образцах из конструкционной стали 40Х16Н9Г2С. Осуществляются один и одна четвертая часть цикла нагружения по этой траектории. Экспериментальные результаты [9] на всех рисунках показаны светлыми кружками. Расчетные результаты показаны сплошными, штриховыми и пунктирными кривыми. Ответные траектории напряжений показаны на рис. 2, а, 3, а, 4, а. Скалярные и векторные свойства – изменение модуля вектора напряжений σ и угла сближения ϑ по траектории деформаций приведены на рис. 2, б, 3, б, 4, б и 2, в, 3, в, 4, в соответственно.

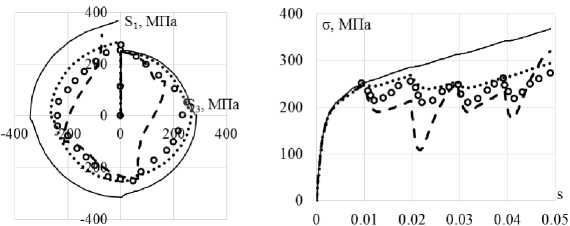
б

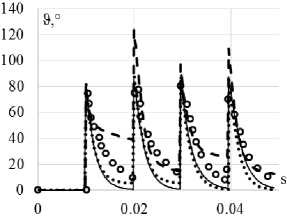
а

в

Рис. 2. Траектория напряжений ( а ); скалярные свойства ( б ); векторные свойства ( в ): кружки – эксперимент; сплошная кривая – теория течения при изотропном упрочнении; пунктирная кривая (точки) – модель Ишлинского–Прагера–Кадашевича–Новожилова; штриховая кривая – модель Оно–Ванга

Fig. 2. Stress path ( а ); scalar properties ( b ); vector properties ( c ): circles show the experiment, a solid curve shows the isotropic hardening of the plastic-flow theory, the dotted curve (points) show Ishlinskii-Prager-Kadashevich model, the dashed curve – shows the Ohno-Wang model

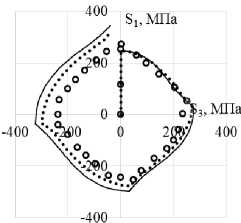
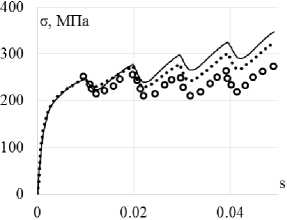
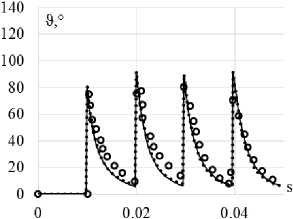
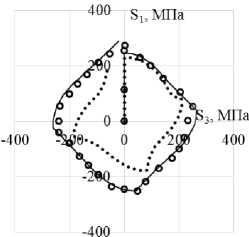
Рис. 3. Траектория напряжений ( а ); скалярные свойства ( б ); векторные свойства ( в ): кружки – эксперимент; сплошная кривая – модель Коротких; пунктирная кривая (точки) – модель Шабоша

а

Fig. 3. Stress path ( а ); scalar properties ( b ); vector properties ( c ): circles show the experiment, the solid curve is Korotkih model, the dotted curve (points) is the Chaboche model

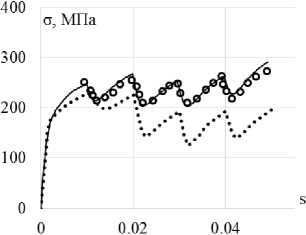
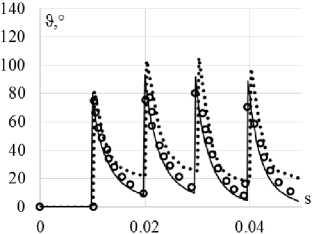
Рис. 4. Траектория напряжений ( а ); скалярные свойства ( б ); векторные свойства ( в ): кружки – эксперимент; сплошная кривая – модель Бондаря; пунктирная кривая (точки) – модельТемиса

Fig. 4. Stress path ( а ); scalar properties ( b ); vector properties ( c ): circles show the experiment, the solid curve shows Bondar model, the dotted curve (points) is Temis model

Сравнительный анализ результатов расчетов по различным вариантам теории и эксперимента показывает:

– по ответной траектории напряжений худшие результаты получены на основе моделей изотропного упрочнения, Оно–Ванга и Темиса; удовлетворительные – на основе моделей Ишлинского–Прагера–Кадашевича– Новожилова, Коротких и Шабоша; наилучшее соответствие эксперименту достигается на основе модели Бондаря;

– по скалярным свойствам худшие результаты получены на основе моделей изотропного упрочнения, Оно–Ванга и Темиса; удовлетворительные – на основе моделей Ишлинского–Прагера–Кадашевича–Новожи-лова, Коротких и Шабоша; наилучшее соответствие эксперименту достигается на основе модели Бондаря;

– по векторным свойствам худшие результаты получены на основе модели Оно–Ванга; удовлетворительные – на основе моделей изотропного упрочнения, Иш-линского–Прагера–Кадашевича–Новожилова, Темиса; наилучшее соответствие эксперименту достигается на основе моделей Коротких, Шабоша и Бондаря.

• 4.    Криволинейная траектория деформаций кусочно-постоянной кривизны

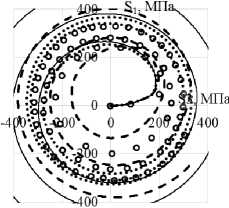
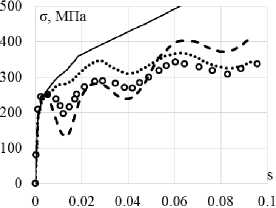
Сравнительный анализ вариантов теорий при сложном нагружении по плоской траектории деформаций кусочно-постоянной кривизны проводится на траекто- рии деформаций (рис. 5) представляющей собой три окружности с радиусами кривизны 0,0025, 0,005, 0,0075, проходящие через начало координат. Эти окружности относятся к траекториям деформаций большой и средней кривизны. Материал, на котором проводится исследование – конструкционная сталь 9Х2. Экспериментальные результаты [9] на всех рисунках показаны светлыми кружками. Расчетные результаты показаны сплошными, штриховыми и пунктирными кривыми. Ответные траектории напряжений показаны на рис. 6, а, 7, а, 8, а. Скалярные и векторные свойства – изменение модуля вектора напряжений σ и угла сближения ϑ по траектории деформаций приведены на рис. 6, б, 7, б, 8, б и 6, в, 7, в, 8, в соответственно.

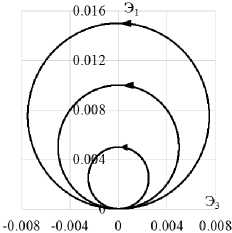
Рис. 5. Траектория деформаций. Окружности

Fig. 5. Strain path. Circles

а

б

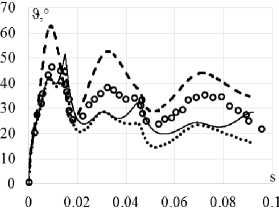
Рис. 6. Траектория напряжений ( а ); скалярные свойства ( б ); векторные свойства ( в ): кружки – эксперимент; сплошная кривая – теория течения при изотропном упрочнении; пунктирная кривая (точки) – модель Ишлинского–Прагера– Кадашевича–Новожилова; штриховая кривая – модель Оно–Ванга

Fig. 6. Stress path ( а ); scalar properties ( b ); vector properties ( c ): circles show the experiment, the solid curve is isotropic hardening of the plastic-flow theory, the dotted curve (points) is Ishlinskii-Prager-Kadashevich model, the dashed curve is Ohno-Wang model

б

в

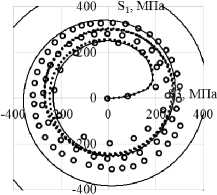
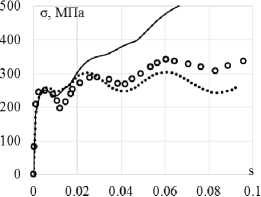
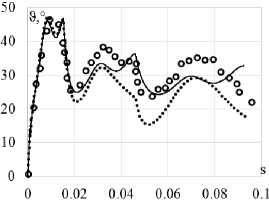
Рис. 7. Траектория напряжений ( а ); скалярные свойства ( б ); векторные свойства ( в ): кружки – эксперимент; сплошная кривая – модель Коротких; пунктирная кривая (точки) – модель Шабоша

Fig. 7. Stress path ( а ); scalar properties ( b ); vector properties ( c ): circles show the experiment, the solid curve is Korotkih model, the dotted curve (points) is Chaboche model

а

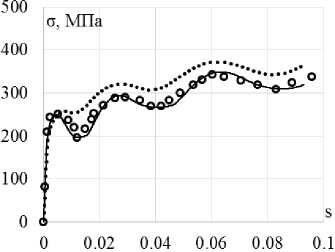
б

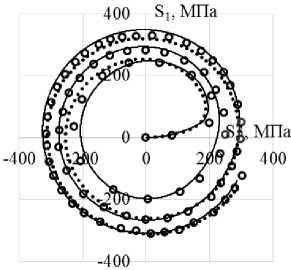
Рис. 8. Траектория напряжений ( а ); скалярные свойства ( б ); векторные свойства ( в ): кружки – эксперимент; сплошная кривая – модель Бондаря; пунктирная кривая (точки) – модельТемиса

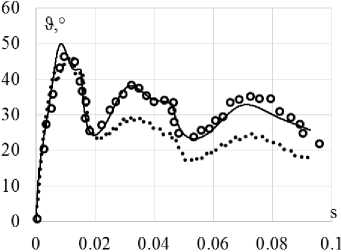
Fig. 8. Stress path ( а ); scalar properties ( b ); vector properties ( c ): circles show the experiment, the solid curve is Bondar model, the dotted curve (points) is Temis model

Сравнительный анализ результатов расчетов по различным вариантам теории и эксперимента показывают:

– по ответным траекториям напряжений худшие результаты получены на основе моделей изотропного упрочнения, Оно–Ванга, Коротких; удовлетворительные – на основе моделей Ищлинского–Прагера– Кадашевича–Новожилова, Шабоша, Темиса; наилучшее соответствие эксперименту достигается на основе модели Бондаря;

– по скалярным свойствам худшие результаты получены на основе моделей изотропного упрочнения, Коротких; удовлетворительные – на основе моделей Оно–Ванга, Ишлинского–Прагера–Кадашевича–Ново-жилова, Шабоша, Темиса; наилучшее соответствие эксперименту достигается на основе модели Бондаря;

– по векторным свойствам удовлетворительные результаты получены на основе моделей изотропного упрочнения, Оно–Ванга, Ишлинского–Прагера–Кадаше-вича–Новожилова, Коротких, Шабоша, Темиса; наилучшее соответствие эксперименту достигается на основе модели Бондаря.

• 5.    Криволинейная траектория деформаций переменной кривизны

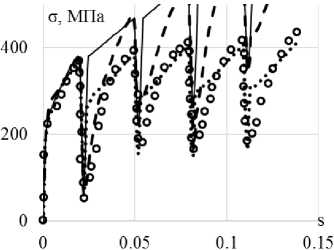
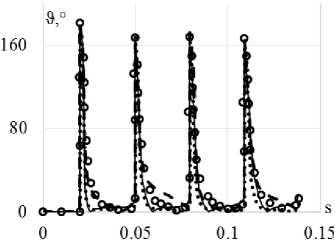
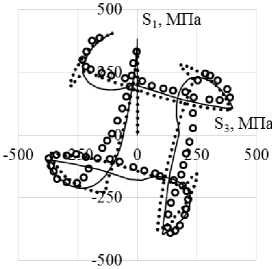
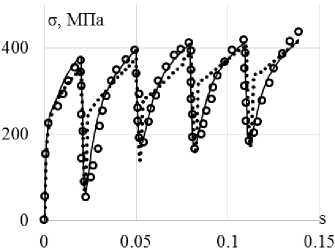
Сравнение вариантов теорий проводится на траектории деформаций переменной кривизны в виде астроиды (рис. 9). Материал, на котором проводятся исследования – конструкционная сталь 9Х2. Экспериментальные результаты [9] на всех рисунках показаны светлыми кружками. Расчетные результаты показаны сплошными, штриховыми и пунктирными кривыми. Ответные траектории напряжений показаны на рис. 10, а , 11, а , 12, а . Скалярные и векторные свойства приведены на рис. 10, б , 11, б , 12, б и 10, в , 11, в , 12, в соответственно.

Сравнительный анализ результатов расчетов по различным вариантам теорий и эксперимента показывают:

• –    по ответным траекториями напряжений худшие результаты получены на основе моделей изотропного упрочнения, Оно–Ванга, Коротких; удовлетворительные – на основе моделей Ишлинского–Прагера–Када-шевича–Новожилова, Шабоша, Темиса; наилучшее соответствие эксперименту достигается на основе модели Бондаря;

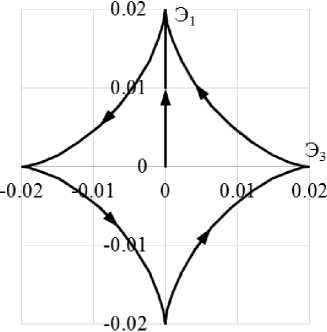
Рис. 9. Траектория деформаций. Астроида

Fig. 9. Strain path. Astroid

• –    по скалярным свойствам худшие результаты получены на основе моделей изотропного упрочнения, Оно–Ванга, Коротких; удовлетворительные – на основе моделей Ишлинского–Прагера–Кадашевича–Новожи-лова, Шабоша, Темиса; наилучшее соответствие эксперименту достигается на основе модели Бондаря;

• –    по векторным свойствам удовлетворительные результаты получены на основе всех вариантов теорий при лучшем соответствии эксперименту модели Бондаря.

  

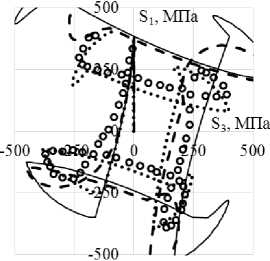
  а

  
  
  
  
  
  
  
  

  б                                         в

  
  

Рис. 10. Траектория напряжений ( а ); скалярные свойства ( б ); векторные свойства ( в ): кружки – эксперимент; сплошная кривая – теория течения при изотропном упрочнении; пунктирная кривая (точки) – модель Ишлинского–Прагера–Кадашевича–Новожилова; штриховая кривая – модель Оно–Ванга

Fig. 10. Stress path ( а ); scalar properties ( b ); vector properties ( c ): circles – experiment, solid curve – isotropic hardening plastic-flow theory, dotted curve (points) – Ishlinskii–Prager–Kadashevich model, dashed curve – Ohno–Wang model

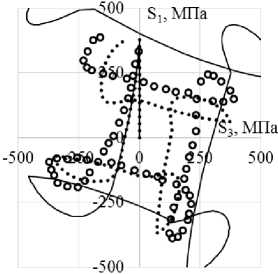
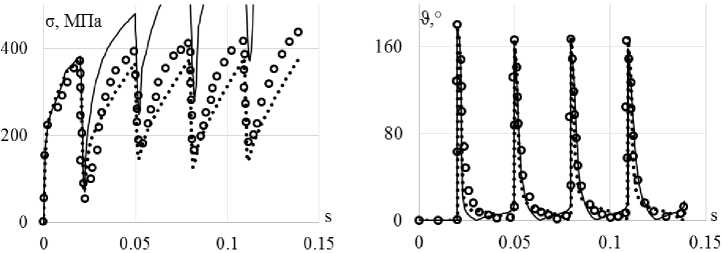
б

в

Рис. 11. Траектория напряжений ( а ); скалярные свойства ( б ); векторные свойства ( в ): кружки – эксперимент; сплошная кривая – модель Коротких; пунктирная кривая (точки) – модель Шабоша

Fig. 11. Stress path ( а ); scalar properties ( b ); vector properties ( c ): circles – experiment, solid curve – Korotkih model, dotted curve (points) – Chaboche model

а

б

Рис. 12. Траектория напряжений ( а ); скалярные свойства ( б ); векторные свойства ( в ): кружки – эксперимент; сплошная кривая – модель Бондаря; пунктирная кривая (точки) – модельТемиса

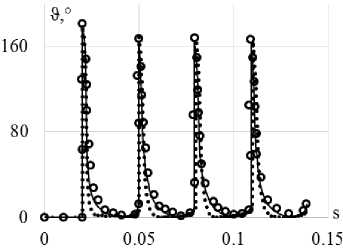
Fig. 12. Stress path ( а ); scalar properties ( b ); vector properties ( c ): circles – experiment, solid curve – Bondar model, dotted curve (points) – Temis model

Заключение

Проведены сравнительные исследования различных вариантов теории пластического течения при комбинированном упрочнении, наиболее используемых в практических расчетах. Рассмотрены три основных класса плоских траекторий деформаций – многозвенные ломаные, криволинейные траектории постоянной и переменной кривизны. Криволинейные траектории являлись траекториями деформаций большой и средней кривизны.

Удовлетворительное соответствие эксперименту по всем траекториям достигается при расчетах на основе моделей Ишлинского–Прагера–Кадашевича–Новожи-лова, Шабоша и Темиса – отличие результатов расчетов