Теории пластичности при сложном нагружении по пространственным траекториям деформаций

ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2021PNRPU MECHANICS BULLETIN

Построение вариантов теорий пластичности, адекватно описывающих процессы сложного нагружения, имеет два основных направления: варианты теории упругопластических процессов [1–8] и варианты теории пластического течения при комбинированном упрочнении [9–25]. Варианты второго направления широко применяются в практических расчетах, так как достаточно просты, имеют обобщения на неизотермические процессы нагружения и позволяют оценивать ресурс.

Оценка работоспособности вариантов теорий пластического течения при комбинированном упрочнении, наиболее применяемых в программных комплексах расчета конструкций, при сложном нагружении является весьма актуальной задачей. В предыдущей работе такая оценка была проведена на плоских траекториях деформаций следующих вариантов теорий: модель изотропного упрочнения, модель Ишлинского – Прагера – Кадашевича – Новожилова [8–10], модель Оно – Ванга [22], модель Армстронга – Фредерика – Кадашевича [11, 13], модель Шабоша [15, 16], модель Темиса [21, 23], модель Бондаря [17–20]. Удовлетворительное соответствие экспериментам [26] достигается при расчетах на основе моделей Ишлинского – Прагера – Кадашеви-ча – Новожилова, Шабоша и Темиса – отличие результатов расчетов и экспериментов не превышает 30 %.

Наилучшее соответствие эксперименту [26] достигается на основе модели Бондаря – отличие результатов и экспериментов не превышает 10 %.

В настоящей работе сравнительный анализ вариантов теорий, удовлетворительно описывающий процессы сложного нагружения по плоским траекториям деформаций, проводится при сложном нагружении по пространственным траекториям деформаций в виде винтовых траекторий постоянной и переменной кривизны и кручения. Результаты расчетов сопоставляются с результатами экспериментов [27, 28].

1.    Варианты теорий пластичности

Рассматриваются конструкционные стали и сплавы однородные и начально изотропные. В процессе деформирования в материале может возникать только пластическая деформационная анизотропия. Рассматриваются малые деформации в условиях отсутствия фазовых превращений, динамических и реологических явлений. Для всех вариантов теории пластического течения при комбинированном упрочнении тензор скоростей деформации 8 у представляется в виде суммы тензоров скоростей упругой s e и пластической s p деформаций:

S j =S ej +s P. (1)

Упругие деформации следуют обобщенному закону Гука:

Таблица 1

Функция изотропного упрочнения. Ст. 45

^s j = E ^[а j ^-v ( ³⁶ о 8 j -a j ) ^] ,            (2)

где E, v - соответственно модуль Юнга и коэффициент Пуассона. „тензор напряжений; „о = 3а,- среднее напряжение.

Принимается поверхность нагружения, разделяющая области упругого и упругопластического состояний. Уравнение поверхности нагружения принимается в следующем виде:

f ( „ j ) = 2 ( s j - ^aj )( s j - ^а иУ C P = 0.         ⁽³⁾

Isotropic hardening function. St. 45

Table 1

p s и *	0	0,0003	0,0006	0,0026	0,0055	0,018	0,027	0,047	0,1
с p , МПа	287	324	341	365	374	405	416	425	432

Здесь s* j = s ij - a ij - девиатор активных [12] напряжений; s_ij – девиатор напряжений; a_ij – девиатор смещения поверхности нагружения, характеризует направленное (анизотропное) упрочнение (девиатор микронапряжений [12]). Скаляр C p ( s Up * ) зависит от накопленной пластической деформации s UP , и отвечает размеру (радиусу) поверхности нагружений, а также характеризует изотропное упрочнение.

Для определения скоростей пластической деформации используется ассоциированный с формулой (3) гра-диентальный закон течения:

Модель Шабоша [15, 16]

M aij =^ajm, aT') = 3gm)si + g^'ar')s .    (7)

m = 1

Здесь, как и ранее, используется модель, состоящая из трех эволюционных уравнений, т.е. M = 3.

Материальные функции стали 45 (табл. 2)

E = 2,1 - 10 5 МПа, v = 0,3,

g(1) = 7070 МПа, g(2) = 5991 МПа, g(3) = 160375 МПа, gW=-0,37, ga2)=-91, ga3)=-2622.

Таблица 2

Функция изотропного упрочнения. Ст. 45

*

Isotropic hardening function. St. 45

s P = d f к = 3 sij s P i,   да ij      „   .  u u

2 а и

.

Здесь „ U

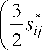
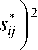
интенсивность активных на-

Table 2

p s и *	0	0,0003	0,0006	0,0026	0,0055	0,018	0,027	0,047	0,1
с p , МПа	287	289	289	289	286	286	289	288	288

.     . p Г 2 . p.p ) 2

ряжений sp*=l 3 sp sp \ скорость накопленной

пластической деформации.

Для всех рассматриваемых вариантов теорий изотропное упрочнение определяется следующей зависи- мостью:

p

p

Рассматриваются следующие варианты, отличающиеся эволюционными уравнениями для смещения центра поверхности нагружения.

Модель Ишлинского – Прагера – Кадашевича – Новожилова [8–10]

a ij = 3 g ^s p .                          ⁽⁶⁾

Материальные функции стали 45 (табл. 1)

E = 2,1 - 10 5 МПа, v = 0,3, g = 6670МПа

Модель Бондаря [17–20]

2 .p Г 2 p Y p aij = 3 g sp +1 3 g sSip + gaaij Is Up* ,          (8)

g = ^Ea ^+в„ a , g s = ^Ea P , g a =^-P .

Материальные функции стали 45 (табл. 3)

E = 2,1 - 10 5 МПа, v = 0,3,

E_a = 6770 МПа , a_a = 140 МПа, в = 265.

Таблица 3

Функции изотропного упрочнения. Ст. 45

Table 3

Isotropic hardening function. St. 45

p s и *	0	0,0003	0,0006	0,0026	0,0055	0,018	0,027	0,047	0,1
с p , МПа	287	314	321	295	266	266	276	285	292

Модель Темиса [21, 23]

a ij = a l ( ^e u * ) ^e ij + a 2 ( ^e u * ) § ij ,                (9)

§ j = K ( a „ , e „p * ) e p .                 (10)

Материальные функции стали 45 получены А.Д. Худяковой и ею проведены расчеты.

Для удобства сопоставления расчетных и экспериментальных результатов рассматривается векторное представление процессов нагружения и деформирования [1]. Расчеты на основе вариантов теорий проводятся на пространственных винтовых траекториях деформаций в пространстве (Э1, Э2, Э3) вектора деформаций Э . Сравнение результатов расчетов и экспериментов [27, 28] осуществляется на компонентах S1, S2, S3 вектора напряжений S вдоль траектории деформаций. Анализируются скалярные свойства – изменение модуля вектора напряжений вдоль траектории деформаций a = a(5).

2.    Винтовая траектория деформаций постоянной кривизны и кручения

Сравнение вариантов теории при сложном нагружении проводится на пространственной траектории деформаций в виде винтовой линии (рис. 1) постоянной кривизны и кручения. В экспериментальных исследованиях [27, 28] реализуются траектории с кривизной от 100 до 333 и круткой от 10 до 666, относящиеся к траекториям от средней до большой кривизны и от малого до большого кручения. Здесь рассматривается винтовая траектория с кривизной и круткой, равными 200. Такую траекторию можно отнести к траектории большой кривизны и большого кручения (50–100 траектории среднего кручения и средней крутки). Экспериментальные исследования [27, 28] проводятся на тонкостенных цилиндрических образцах из стали 45 под действием осевой силы, крутящего момента и внутреннего давления

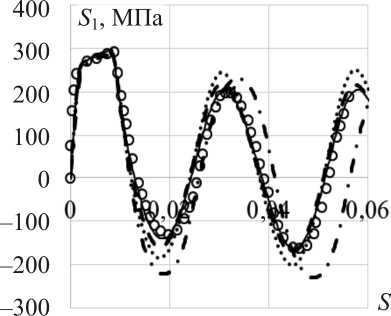
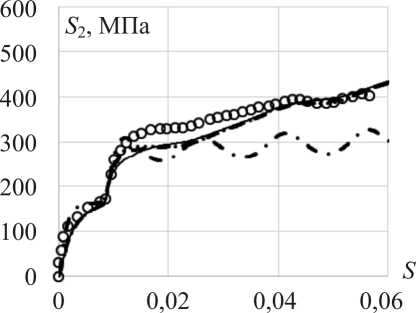
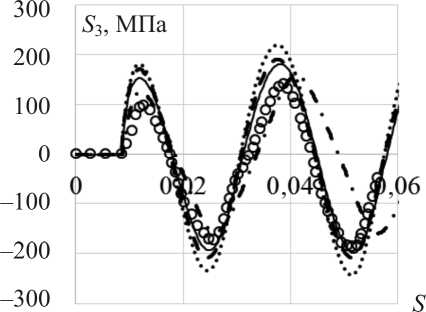
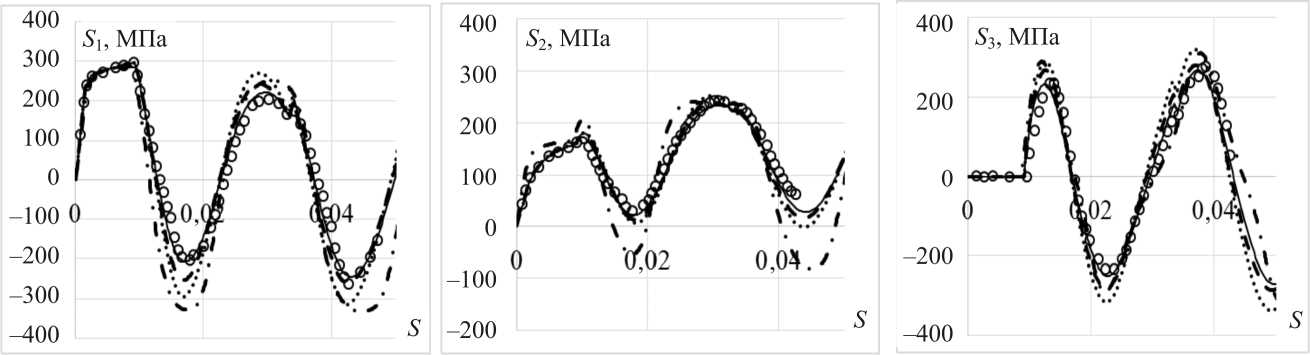
( P , M , q - опыты ) . Экспериментальные результаты [27, 28] на всех рисунках показаны светлыми кружками, а расчетные – сплошными, штрихпунктирными, штриховыми и пунктирными (точками) кривыми. Изменения компонент вектора напряжений S 1 , S ₂, S ₃ вдоль траектории деформаций, т.е. как функции длины дуги траектории деформаций s , показаны соответственно на рис. 2 ( а–в ). Скалярные свойства – изменение модуля вектора напряжений a вдоль траектории деформаций приведены на рис. 3.

Сравнительный анализ результатов расчетов по различным вариантам теорий и эксперимента [27, 28] показывает:

– по компонентам вектора напряжений худшие результаты получены на основе модели Темиса; удовлетворительные – на основе модели Ишлинского – Прагера – Кадашевича – Новожилова; наилучшее соответствие эксперименту достигается на основе моделей Шабоша и Бондаря при лучшем соответствии эксперименту модели Бондаря;

– по скалярным свойствам худший результат получен на основе модели Темиса; наилучшее соответствие эксперименту достигается на основе моделей Ишлин-ского – Прагера – Кадашевича – Новожилова, Шабоша и Бондаря.

а                                       б                                          в

Рис. 2. Изменение компоненты: а – S ₁ вектора напряжений вдоль траектории деформаций; б – S ₂ вектора напряжений вдоль траектории деформаций; в – S ₃ вектора напряжений вдоль траектории деформаций

Fig. 2. Change in the component: а – S ₁ of the stress vector along the deformation trajectory; б – S ₂ of the stress vector along the deformation trajectory; в – S ₃ of the stress vector along the deformation trajectory

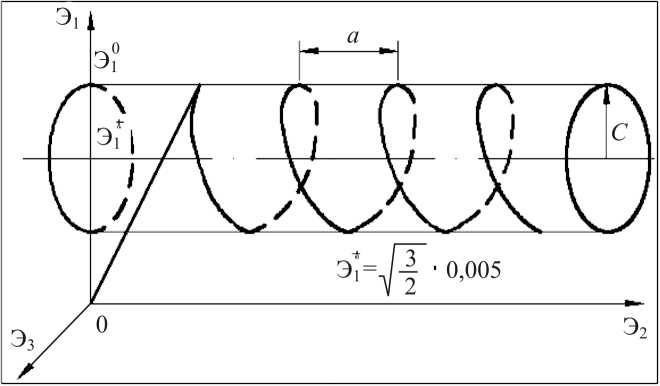
Рис. 1. Траектория деформаций

Fig. 1. Deformation trajectory

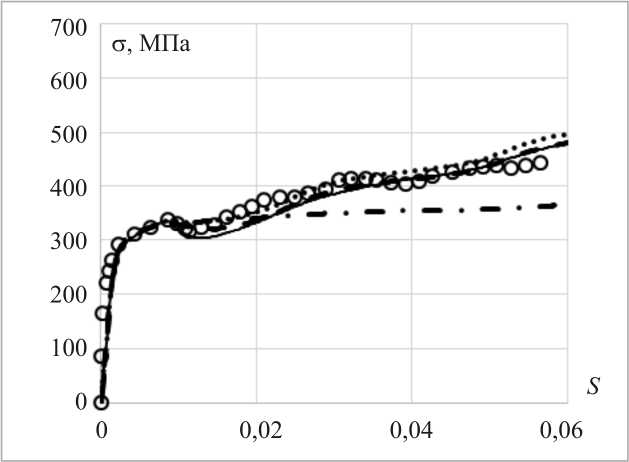
Рис. 3. Скалярные свойства (кружки – эксперимент, сплошная кривая – модель Бондаря, пунктирная кривая (точки) – модель Ишлинского – Прагера – Кадашевича –

Новожилова, штриховая кривая – модель Шабоша, штрихпунктирная кривая – модель Темиса)

Fig. 3. Scalar properties (circles – experiment, solid curve –

Bondar model, dashed curve (points) – Ishlinskii – Prager – Kadashevich model, dotted curve – Chaboche model, dashpoint curve – Temis model)

3.    Винтовая траектория деформаций переменной кривизны и кручения

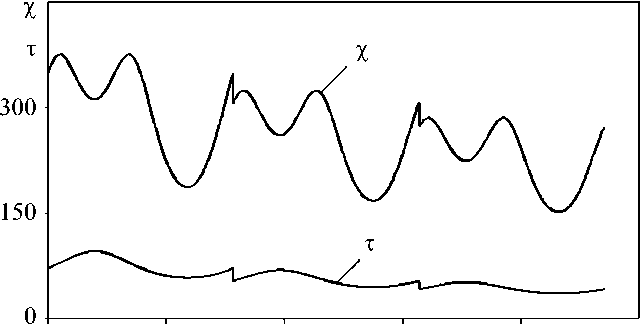
Сравнительный анализ вариантов теорий проводится при сложном нагружении по пространственной траектории деформаций в виде винтовой линии с переменной кривизной и кручением. Экспериментальные исследования [27, 28] проводятся на трубчатых образцах из стали 45. На рис. 4 показаны изменения кривизны и крутки вдоль траектории деформаций. Здесь кривизна меняется от 150 до 370, а крутка – от 50 до 100. Таким образом, рассматриваемую траекторию можно отнести к траектории большой кривизны и среднего кручения. На всех рисунках экспериментальные результаты пока- заны светлыми кружками, а расчетные – сплошными, штрихпунктирными, штриховыми и пунктирными (точками) кривыми. Изменения компонент вектора напряжений S1, S2, S3 вдоль траектории деформаций показаны соответственно на рис. 5 (а–в). Скалярные свойства – изменение модуля вектора напряжений σ вдоль траектории деформаций приведено на рис. 6.

Сравнительный анализ результатов расчетов по различным вариантам теорий и эксперимента [27, 28] показывает:

• –    по компонентам вектора напряжений худшие результаты получены на основе моделей Темиса и Иш-линского – Прагера – Кадашевича – Новожилова; удовлетворительный – на основе модели Шабоша; наилучшее соответствие эксперименту достигается на основе модели Бондаря;

• –    по скалярным свойствам худшие результаты получены на основе моделей Темиса и Ишлинского – Прагера – Кадашевича – Новожилова; удовлетворительный – на основе модели Шабоша; наилучшее соответствие эксперименту достигается на основе модели Бондаря.

0       0,01        0,02       0,03       0,04       5

Рис. 4. Изменение кривизны χ и крутки τ вдоль траектории деформации

Fig. 4. Change in curvature χ and twist τ along the deformation trajectory

а                                       б                                       в

Рис. 5. Изменение компоненты: а – S ₁ вектора напряжений вдоль траектории деформаций; б – S ₂ вектора напряжений вдоль траектории деформаций; в – S ₃ вектора напряжений вдоль траектории деформаций

Fig. 5. Change in the component: а – S ₁ of the stress vector along the deformation trajectory; б – S ₂ of the stress vector along the deformation trajectory; в – S ₃ of the stress vector along the deformation trajectory

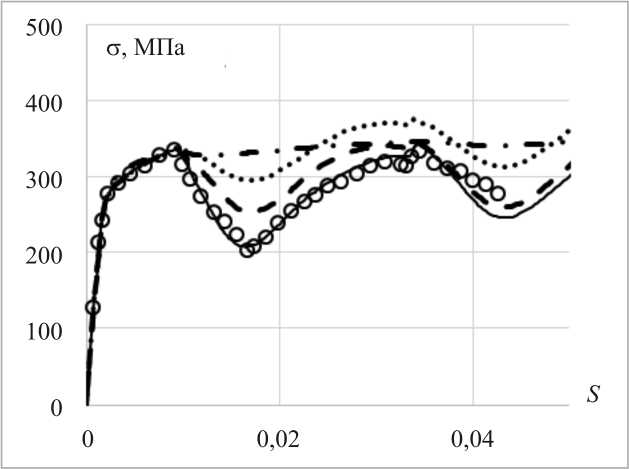
Рис. 6. Скалярные свойства (кружки – эксперимент, сплошная кривая – модель Бондаря, пунктирная кривая – модель Ишлинского – Прагера – Кадашевича – Новожилова, штриховая кривая – модель Шабоша, штрихпунктирная кривая – модель Темиса)

Figure 6. Scalar properties (circles – experiment, solid curve – Bondar model, dashed curve (points) – Ishlinskii – Prager – Kadashevich model, dotted curve – Chaboche model, dashpoint curve – Temis model)

Заключение

Проведены сравнения различных вариантов теории пластического течения при комбинированном упрочнении наиболее используемых в практических расчетах и показавших себя при сравнительных исследованиях при сложном нагружении по плоским траекториям деформаций. Рассмотрена пространственная траектория деформаций в виде винтовой линии постоянной кривизны и кручения (кривизна 200, крутка 200), которая относится к траектории большой кривизны и большого кручения. Рассмотрена также пространственная траектория деформаций в виде винтовой линии переменной кривизны и кручения (кривизна меняется от 150 до 370, а крутка – от 50 до 100), которую можно отнести к траектории большой кривизны и среднего кручения.