Теория делимости и простые числа
Автор: Елизаров Е.Б.
Журнал: Теория и практика современной науки @modern-j
Статья в выпуске: 6-1 (12), 2016 года.
Бесплатный доступ
Статья является продолжением темы «Последняя теорема Ферма и тройки Пифагора» в №5(11)2016г.е-журнала «Теория и практика современной науки» и посвящена Теории делимости, определенной еще Пифагором, а также Простым числам, играющим важную роль в Теории чисел. В данной статье рассматриваются элементарные построения Теории делимости, а также определения и нахождения Простых чисел.
Тройки пифагора, теория делимости, простые числа
Короткий адрес: https://sciup.org/140269168
IDR: 140269168
Текст научной статьи Теория делимости и простые числа
1. История вопроса.
-
[1] Главным достижением школы Пифагора было построение «Теории делимости». Они разбивали все натуральные числа на четные и нечетные, простые и составные. Пифагор говорил: «Все есть число!».
-
[2] Мне хотелось бы рассказать вам сегодня о предмете, которым я сам хотя и не занимался, но который всегда чрезвычайно привлекал меня и который пленяет математиков, начиная с незапамятных времен вплоть до настоящего времени, а именно, о вопросе распределения простых чисел.
Вы, безусловно, все знаете, что простым числом является всякое натуральное число, большее чем 1, которое не делится ни на одно из натуральных чисел, кроме 1. По крайней мере такое определение дают специалисты в области теории чисел;
Распределение простых чисел характеризуется двумя особенностями, о которых я предполагаю рассказать настолько убедительно, что вы постоянно будете помнить о них.
Во-первых, несмотря на простое определение простых чисел и скромную роль «кирпичиков» для построения натуральных чисел, простые числа принадлежат к в высшей степени случайным пренебрегающим всеми правилами объектам, изучаемым математиками: они подобно сорной траве появляются среди натуральных чисел, не подчиняясь, кажется, никаким законам, только случаю, и никто не может заранее предсказать, где даст росток следующее простое число.
Вторая особенность еще более удивительна, поскольку здесь имеет место совсем противоположный факт, а именно, простые числа проявляют ошеломляющую регулярность, существуют законы, определяющие их поведение, и подчиняются они этим законам почти с воинской дисциплинированностью.
Я думаю, вы согласитесь, что явных объяснений, почему одно число является простым, а другое нет, не существует. Даже, наоборот, глядя на эти числа, возникает такое чувство, что перед тобой одна из необъяснимых тайн мироздания. Тот факт, что даже математикам не удается постичь эту тайну, возможно наиболее убедительно доказывается тем рвением, с которым они отыскивают все большие и большие простые числа, оперируя с регулярно возрастающими числами, подобно квадратам или степеням двух. Никто и никогда не станет утруждать себя поисками и регистрацией результатов, превосходящих уже известные, но, когда речь заходит о простых числах, люди, доставляя себе массу трудностей, поступают именно таким образом.
X р(х)~----- log x
Это соотношение (получившее доказательство лишь в 1896 г.) известно как асимптотический закон распределения простых чисел . Гаусс, величайший математик мира, открыл его в пятнадцатилетнем возрасте, изучая таблицы простых чисел, помещенные в подаренной ему годом раньше книге логарифмов. В течение всей своей жизни Гаусс увлеченно занимался изучением вопроса распределения простых чисел, в связи с чем ему пришлось выполнить массу вычислений. В одном из писем к Энке он пишет, как он «довольно часто, имея свободными минут пятнадцать, занимался просчитыванием очередной тысячи (т. е. интервала в 1000 чисел)», пока, наконец, не перечислил все простые числа вплоть до 3 000 000 (!) и не сравнил их распределение с результатами, полученными с помощью выведенной им формулы.
2. Правила делимости.
При составлении таблицы 1. Тройки Пифагора (до 1000) - видно, что появились новые свойства, в частности для Y:
-
2.1. Приведенные уравнения для нечетных чисел характеризуются
-
2.2. В общем виде, если
-
2.2.1. Далее много интересных соотношений:
m = 1N из формул Евклида Y = M2 –N2 , тогда Y = (N×1 + 1)2 – N2= N2 + 2N + 12 - N2 = (2N + 1), т.е. в приведенных уравнениях вида Y= 2N+1 – результатом являются все нечетные числа натурального ряда.
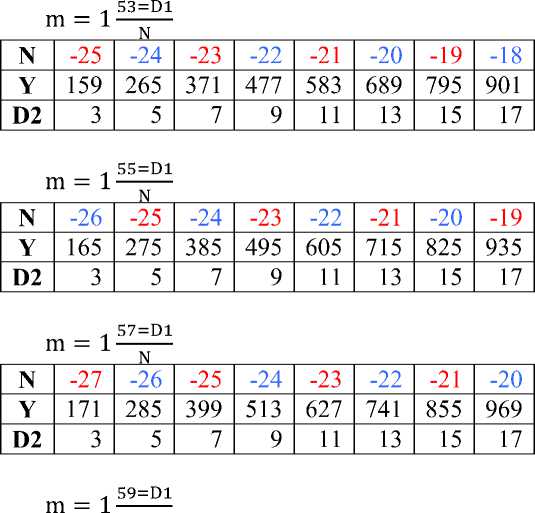
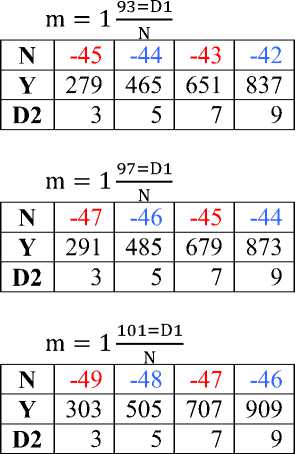
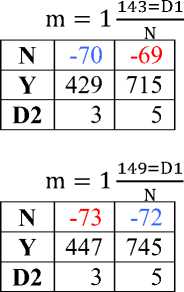
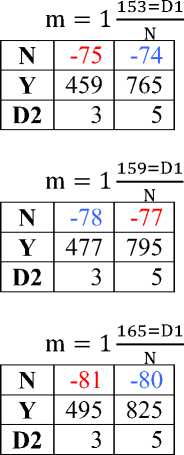
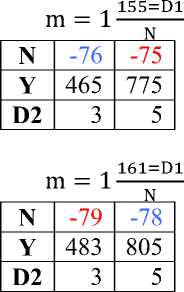
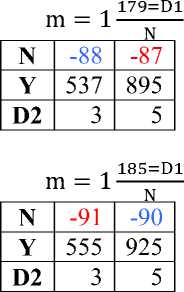
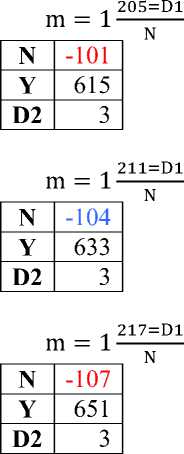
D m = 1N из формул Евклида Y = M2 –N2, тогда Y = (N×1 + D)2 – N2= N2 + 2ND + D2 - N2= D (D+2 N), т.е. все уравнения вида Y= D (D+2N) - делятся на D, следовательно, все нечетные целые числа натурального ряда, которые имеют делители, имеют эту форму и на основании этого свойства строится Таблица 2. Правила делимости (до 1000).
Уравнение Y= D (D+2N) можно записать по другому: D2 + 2ND - Y = 0 (18)
Корни этого урав нения
D1.2 = -N ± √N2 + Y, т.е. всегда два корня (два делителя).
Если
D1
m=1N1
то D1 при N1, аналогично D2 при N2 - возможны даже (-N2) – на противоположных концах таблицы - но тогда значения (+N1) и (-N2) - равны по абсолютной величине, а D1 и D2 меняются своими числовыми значениями по концам таблицы 2.
Далее, в корнях уравнении (18) дискриминант √N2 + Y = N + D1
всегда имеет точное решение, которое можно проверить.
3.Простые числа.
При рассмотрении правил делимости - появился логичный вывод, если какое-то значение Y фигурирует в тройках Пифагора несколько раз, то разумеется - оно составное, тогда:
-
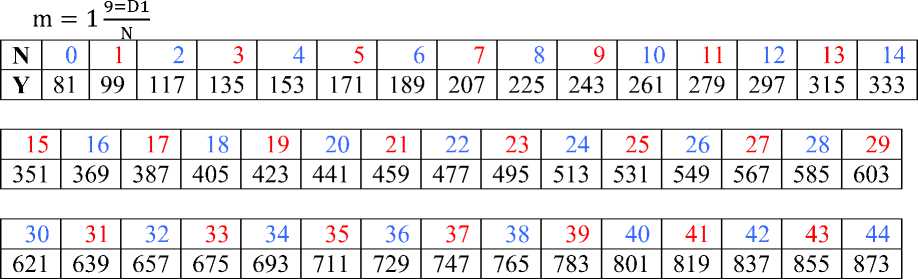
- простые числа – это оставшиеся нечетные числа натурального ряда Y= 2N+1 отсеянные от всех чисел вида Y= D (D+2N), т.е. за минусом арифметических прогрессий (32 + 2N×3), (52 + 2N×5), (72 + 2N×7) и т.д. - в итоге получается Таблица 3.Нахождение простых чисел (до 1000).
Далее из этой таблицы берем часть для m = 1 1 , т.е. натуральный ряд нечетных чисел (с затушеванными составными числами и «цвет»-простыми числами), и видоизменяем форму таблицы, введя параметры: столбцы ∑=1, ∑=3, ∑=5, ∑=7, ∑=9, ∑=2, ∑=4, ∑=6, ∑=8 – в результате получится Таблица 3.1.Сводная таблица из Таблицы 3.
Далее: исключив за ненадобностью столбцы ∑=3, ∑=6, ∑=9)– в результате получится Таблица 3.2.Правленая сводная таблица из Таблицы 3.1.
Далее: очистив Таблицу 3.2. от вспомогательных пометок, добавляем следующие параметры: код строки (составляется из последних цифр чисел), № дома (формируется цикличностью кодов строк) – получаем Таблицу 3.3. Простые и некоторые составные числа (до 1000).
Примечательно, что все простые числа обрели прописку: № дома (пять строк), код каждой строки. Данную таблицу можно строить до любого предела, проверять количество простых чисел в определенных пределах – это основное достижение этой работы.
ЗАКЛЮЧЕНИЕ:
-
1. Формулы для построения Таблицы 1.Тройки Пифагора (до 1000), в частности для Y, дали интересные соотношения, которые были использованы для построения Таблицы 2. Правила делимости (до 1000)
-
- в данном случае для нечетных чисел, и методом отсеивания получена Таблица 3. Нахождения простых чисел (до 1000). В окончании с новыми преобразованиями была построена Таблица 3.3. Простые и некоторые составные числа (до1000) - можно оставить в ней только простые числа.
-
2. Проверка чисел: простые или со ставны е производится по формуле √N2 + Y
-
3. Мы стремились решить задачу, выстраивая цепочку логических аргументов, приводящую к правильному заключению. Истинность математической теории, проявляется в глубине открытия знаний и логичности математической конструкции.
Если единственное решение – число простое, если несколько решений – число составное.
Таблица 2. Правила делимости (до 1000).
N
3=D1 m=1
|
N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
Y |
9 |
15 |
21 |
27 |
33 |
39 |
45 |
51 |
57 |
63 |
69 |
75 |
81 |
87 |
93 |
99 |
105 |
111 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
31 |
33 |
35 |
37 |
|
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
|
117 |
123 |
129 |
135 |
141 |
147 |
153 |
159 |
165 |
171 |
177 |
183 |
189 |
195 |
201 |
|
39 |
41 |
43 |
45 |
47 |
49 |
51 |
53 |
55 |
57 |
59 |
61 |
63 |
65 |
67 |
|
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
|
207 |
213 |
219 |
225 |
231 |
237 |
243 |
249 |
255 |
261 |
267 |
273 |
279 |
285 |
291 |
|
69 |
71 |
73 |
75 |
77 |
79 |
81 |
83 |
85 |
87 |
89 |
91 |
93 |
95 |
97 |
|
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
60 |
61 |
62 |
|
297 |
303 |
309 |
315 |
321 |
327 |
333 |
339 |
345 |
351 |
357 |
363 |
369 |
375 |
381 |
|
99 |
101 |
103 |
105 |
107 |
109 |
111 |
113 |
115 |
117 |
119 |
121 |
123 |
125 |
127 |
|
63 |
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
72 |
73 |
74 |
75 |
76 |
77 |
|
387 |
393 |
399 |
405 |
411 |
417 |
423 |
429 |
435 |
441 |
447 |
453 |
459 |
465 |
471 |
|
129 |
131 |
133 |
135 |
137 |
139 |
141 |
143 |
145 |
147 |
149 |
151 |
153 |
155 |
157 |
|
78 |
79 |
80 |
81 |
82 |
83 |
84 |
85 |
86 |
87 |
88 |
89 |
90 |
91 |
92 |
|
477 |
483 |
489 |
495 |
501 |
507 |
513 |
519 |
525 |
531 |
537 |
543 |
549 |
555 |
561 |
|
159 |
161 |
163 |
165 |
167 |
169 |
171 |
173 |
175 |
177 |
179 |
181 |
183 |
185 |
187 |
|
93 |
94 |
95 |
96 |
97 |
98 |
99 |
100 |
101 |
102 |
103 |
104 |
105 |
106 |
107 |
|
567 |
573 |
579 |
585 |
591 |
597 |
603 |
609 |
615 |
621 |
627 |
633 |
639 |
645 |
651 |
|
189 |
191 |
193 |
195 |
197 |
199 |
201 |
203 |
205 |
207 |
209 |
211 |
213 |
215 |
217 |
|
108 |
109 |
110 |
111 |
112 |
113 |
114 |
115 |
116 |
117 |
118 |
119 |
120 |
121 |
122 |
|
657 |
663 |
669 |
675 |
681 |
687 |
693 |
699 |
705 |
711 |
717 |
723 |
729 |
735 |
741 |
|
219 |
221 |
223 |
225 |
227 |
229 |
231 |
233 |
235 |
237 |
239 |
241 |
243 |
245 |
247 |
|
123 |
124 |
125 |
126 |
127 |
128 |
129 |
130 |
131 |
132 |
133 |
134 |
135 |
136 |
137 |
|
747 |
753 |
759 |
765 |
771 |
777 |
783 |
789 |
795 |
801 |
807 |
813 |
819 |
825 |
831 |
|
249 |
251 |
253 |
255 |
257 |
259 |
261 |
263 |
265 |
267 |
269 |
271 |
273 |
275 |
277 |
|
138 |
139 |
140 |
141 |
142 |
143 |
144 |
145 |
146 |
147 |
148 |
149 |
150 |
151 |
152 |
|
837 |
843 |
849 |
855 |
861 |
867 |
873 |
879 |
885 |
891 |
897 |
903 |
909 |
915 |
921 |
|
279 |
281 |
283 |
285 |
287 |
289 |
291 |
293 |
295 |
297 |
299 |
301 |
303 |
305 |
307 |
|
153 |
154 |
155 |
156 |
157 |
158 |
159 |
160 |
161 |
162 |
163 |
164 |
165 |
|
927 |
933 |
939 |
945 |
951 |
957 |
963 |
969 |
975 |
981 |
987 |
993 |
999 |
|
309 |
311 |
313 |
315 |
317 |
319 |
321 |
323 |
325 |
327 |
329 |
331 |
333 |
|
5=D1 m=1 N |
||||||||||||||||
|
N |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
Y |
15 |
25 |
35 |
45 |
55 |
65 |
75 |
85 |
95 |
105 |
115 |
125 |
135 |
145 |
155 |
165 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
31 |
33 |
|
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
|
175 |
185 |
195 |
205 |
215 |
225 |
235 |
245 |
255 |
265 |
275 |
285 |
295 |
305 |
315 |
|
35 |
37 |
39 |
41 |
43 |
45 |
47 |
49 |
51 |
53 |
55 |
57 |
59 |
61 |
63 |
|
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
|
325 |
335 |
345 |
355 |
365 |
375 |
385 |
395 |
405 |
415 |
425 |
435 |
445 |
455 |
465 |
|
65 |
67 |
69 |
71 |
73 |
75 |
77 |
79 |
81 |
83 |
85 |
87 |
89 |
91 |
93 |
|
45 |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
|
475 |
485 |
495 |
505 |
515 |
525 |
535 |
545 |
555 |
565 |
575 |
585 |
595 |
605 |
615 |
|
95 |
97 |
99 |
101 |
103 |
105 |
107 |
109 |
111 |
113 |
115 |
117 |
119 |
121 |
123 |
|
60 |
61 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
72 |
73 |
74 |
|
625 |
635 |
645 |
655 |
665 |
675 |
685 |
695 |
705 |
715 |
725 |
735 |
745 |
755 |
765 |
|
125 |
127 |
129 |
131 |
133 |
135 |
137 |
139 |
141 |
143 |
145 |
147 |
149 |
151 |
153 |
|
75 |
76 |
77 |
78 |
79 |
80 |
81 |
82 |
83 |
84 |
85 |
86 |
87 |
88 |
89 |
|
775 |
785 |
795 |
805 |
815 |
825 |
835 |
845 |
855 |
865 |
875 |
885 |
895 |
905 |
915 |
|
155 |
157 |
159 |
161 |
163 |
165 |
167 |
169 |
171 |
173 |
175 |
177 |
179 |
181 |
183 |
|
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
|
925 |
935 |
945 |
955 |
965 |
975 |
985 |
995 |
|
185 |
187 |
189 |
191 |
193 |
195 |
197 |
199 |
|
7=D1 m=1 N |
|||||||||||||||
|
N |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Y |
21 |
35 |
49 |
63 |
77 |
91 |
105 |
119 |
133 |
147 |
161 |
175 |
189 |
203 |
217 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
31 |
|
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
|
231 |
245 |
259 |
273 |
287 |
301 |
315 |
329 |
343 |
357 |
371 |
385 |
399 |
413 |
427 |
|
33 |
35 |
37 |
39 |
41 |
43 |
45 |
47 |
49 |
51 |
53 |
55 |
57 |
59 |
61 |
|
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
|
441 |
455 |
469 |
483 |
497 |
511 |
525 |
539 |
553 |
567 |
581 |
595 |
606 |
623 |
637 |
|
63 |
65 |
67 |
69 |
71 |
73 |
75 |
77 |
79 |
81 |
83 |
85 |
87 |
89 |
91 |
|
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
57 |
|
651 |
665 |
679 |
693 |
707 |
721 |
735 |
749 |
763 |
777 |
791 |
805 |
819 |
833 |
847 |
|
93 |
95 |
97 |
99 |
101 |
103 |
105 |
107 |
109 |
111 |
113 |
115 |
117 |
119 |
121 |
|
58 |
59 |
60 |
61 |
62 |
63 |
64 |
65 |
66 |
67 |
|
861 |
875 |
889 |
903 |
917 |
931 |
945 |
959 |
973 |
987 |
|
123 |
125 |
127 |
129 |
131 |
133 |
135 |
137 |
139 |
141 |
|
9=D1 m=1 N |
|||||||||||||||
|
N |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Y |
27 |
45 |
63 |
81 |
99 |
117 |
135 |
153 |
171 |
189 |
207 |
225 |
243 |
261 |
279 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
31 |
|
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
|
297 |
315 |
333 |
351 |
369 |
387 |
405 |
423 |
441 |
459 |
477 |
495 |
513 |
531 |
549 |
|
33 |
35 |
37 |
39 |
41 |
43 |
45 |
47 |
49 |
51 |
53 |
55 |
57 |
59 |
61 |
|
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
|
567 |
585 |
603 |
621 |
639 |
657 |
675 |
693 |
711 |
729 |
747 |
765 |
783 |
801 |
819 |
|
63 |
65 |
67 |
69 |
71 |
73 |
75 |
77 |
79 |
81 |
83 |
85 |
87 |
89 |
91 |
11=D1 N
|
N |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Y |
33 |
55 |
77 |
99 |
121 |
143 |
165 |
187 |
209 |
231 |
253 |
275 |
297 |
319 |
341 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
31 |
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
363 |
385 |
407 |
429 |
451 |
473 |
495 |
517 |
539 |
561 |
583 |
605 |
627 |
649 |
671 |
|
33 |
35 |
37 |
39 |
41 |
43 |
45 |
47 |
49 |
51 |
53 |
55 |
57 |
59 |
61 |
|
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
|
693 |
715 |
737 |
759 |
781 |
803 |
825 |
847 |
869 |
891 |
913 |
935 |
957 |
979 |
|
63 |
65 |
67 |
69 |
71 |
73 |
75 |
77 |
79 |
81 |
83 |
85 |
87 |
89 |
13=D1 m=1
N
|
N |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Y |
39 |
65 |
91 |
117 |
143 |
169 |
195 |
221 |
247 |
273 |
299 |
325 |
351 |
377 |
403 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
31 |
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
429 |
455 |
481 |
507 |
533 |
559 |
585 |
611 |
637 |
663 |
689 |
715 |
741 |
767 |
793 |
|
33 |
35 |
37 |
39 |
41 |
43 |
45 |
47 |
49 |
51 |
53 |
55 |
57 |
59 |
61 |
|
25 |
26 |
27 |
28 |
29 |
30 |
31 |
|
819 |
845 |
871 |
897 |
923 |
949 |
975 |
|
63 |
65 |
67 |
69 |
71 |
73 |
75 |
15=D1 m=1
|
N |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Y |
45 |
75 |
105 |
135 |
165 |
195 |
225 |
255 |
285 |
315 |
345 |
375 |
405 |
435 |
465 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
31 |
|
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
495 |
525 |
555 |
585 |
615 |
645 |
675 |
705 |
735 |
765 |
795 |
825 |
855 |
885 |
915 |
|
33 |
35 |
37 |
39 |
41 |
43 |
45 |
47 |
49 |
51 |
53 |
55 |
57 |
59 |
61 |
|
24 |
25 |
|
945 |
975 |
|
63 |
65 |
17=D1 m = 1 17=D1 N
|
N |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Y |
51 |
85 |
119 |
153 |
187 |
221 |
255 |
289 |
323 |
357 |
391 |
425 |
459 |
493 |
527 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
31 |
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
561 |
595 |
629 |
663 |
697 |
731 |
765 |
799 |
833 |
867 |
901 |
935 |
969 |
|
33 |
35 |
37 |
39 |
41 |
43 |
45 |
47 |
49 |
51 |
53 |
55 |
57 |
19=D1 m = 1 19=D1 N
|
N |
-8 |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Y |
57 |
95 |
133 |
171 |
209 |
247 |
285 |
323 |
361 |
399 |
437 |
475 |
513 |
551 |
589 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
31 |
|
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
627 |
665 |
703 |
741 |
779 |
817 |
855 |
893 |
931 |
969 |
|
33 |
35 |
37 |
39 |
41 |
43 |
45 |
47 |
49 |
51 |
21=D1 m = 1 21=D1 N
|
N |
-9 |
-8 |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
Y |
63 |
105 |
147 |
189 |
231 |
273 |
315 |
357 |
399 |
441 |
483 |
525 |
567 |
609 |
651 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
31 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
693 |
735 |
777 |
819 |
861 |
903 |
945 |
987 |
|
33 |
35 |
37 |
39 |
41 |
43 |
45 |
47 |
23=D1 m=1
N
|
N |
-10 |
-9 |
-8 |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
Y |
69 |
115 |
161 |
207 |
253 |
299 |
345 |
391 |
437 |
483 |
529 |
575 |
621 |
667 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
713 |
759 |
805 |
851 |
897 |
943 |
989 |
|
31 |
33 |
35 |
37 |
39 |
41 |
43 |
|
25=D1 m=1 N |
||||||||||||||
|
N |
-11 |
-10 |
-9 |
-8 |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
|
Y |
75 |
125 |
175 |
225 |
275 |
325 |
375 |
425 |
475 |
525 |
575 |
625 |
675 |
725 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
|
3 |
4 |
5 |
6 |
7 |
||||||||||
|
775 |
825 |
875 |
925 |
975 |
||||||||||
|
31 |
33 |
37 |
39 |
41 |
||||||||||
|
27=D1 m = 1 27=D1 N |
||||||||||||||
|
N |
-12 |
-11 |
-10 |
-9 |
-8 |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
|
Y |
81 |
135 |
189 |
243 |
297 |
351 |
405 |
459 |
513 |
567 |
621 |
675 |
729 |
783 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
|
2 |
3 |
4 |
5 |
|||||||||||
|
837 |
891 |
945 |
999 |
|||||||||||
|
31 |
33 |
37 |
39 |
|||||||||||
|
29=D1 m=1 N |
||||||||||||||
|
N |
-13 |
-12 |
-11 |
-10 |
-9 |
-8 |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
|
Y |
87 |
145 |
203 |
261 |
319 |
377 |
435 |
493 |
551 |
609 |
667 |
725 |
783 |
841 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
|
1 |
2 |
|||||||||||||
|
899 |
957 |
|||||||||||||
|
31 |
33 |
|||||||||||||
|
31=D1 m=1 N |
||||||||||||||
|
N |
-14 |
-13 |
-12 |
-11 |
-10 |
-9 |
-8 |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
|
Y |
93 |
155 |
217 |
279 |
341 |
403 |
465 |
527 |
589 |
651 |
713 |
775 |
837 |
899 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
33=D1 m=1
N
|
N |
-15 |
-14 |
-13 |
-12 |
-11 |
-10 |
-9 |
-8 |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
|
Y |
99 |
165 |
231 |
297 |
363 |
429 |
495 |
561 |
627 |
693 |
759 |
825 |
891 |
957 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
35=D1 m=1
N
|
N |
-16 |
-15 |
-14 |
-13 |
-12 |
-11 |
-10 |
-9 |
-8 |
-7 |
-6 |
-5 |
-4 |
|
Y |
105 |
175 |
245 |
315 |
385 |
455 |
525 |
595 |
665 |
735 |
805 |
875 |
945 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
37=D1 m=1
N
|
N |
-17 |
-16 |
-15 |
-14 |
-13 |
-12 |
-11 |
-10 |
-9 |
-8 |
-7 |
-6 |
-5 |
|
Y |
111 |
185 |
259 |
333 |
407 |
481 |
555 |
629 |
703 |
777 |
851 |
925 |
999 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
39=D1 m=1
N
|
N |
-18 |
-17 |
-16 |
-15 |
-14 |
-13 |
-12 |
-11 |
-10 |
-9 |
-8 |
-7 |
|
Y |
117 |
195 |
273 |
351 |
429 |
507 |
585 |
663 |
741 |
819 |
897 |
975 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
41=D1 m = 1 41=D1 N
|
N |
-19 |
-18 |
-17 |
-16 |
-15 |
-14 |
-13 |
-12 |
-11 |
-10 |
-9 |
|
Y |
123 |
205 |
287 |
369 |
451 |
533 |
615 |
697 |
779 |
861 |
943 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
43=D1 m=1
N
|
N |
-20 |
-19 |
-18 |
-17 |
-16 |
-15 |
-14 |
-13 |
-12 |
-11 |
-10 |
|
Y |
129 |
215 |
301 |
387 |
473 |
559 |
645 |
731 |
817 |
903 |
989 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
45=D1 m=1
N
|
N |
-21 |
-20 |
-19 |
-18 |
-17 |
-16 |
-15 |
-14 |
-13 |
-12 |
|
Y |
135 |
225 |
315 |
405 |
495 |
585 |
675 |
765 |
855 |
945 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
47=D1 m=1
|
N |
-22 |
-21 |
-20 |
-19 |
-18 |
-17 |
-16 |
-15 |
-14 |
-13 |
|
Y |
141 |
235 |
329 |
423 |
517 |
611 |
705 |
799 |
893 |
987 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
49=D1 m = 1 49=D1 N
|
N |
-23 |
-22 |
-21 |
-20 |
-19 |
-18 |
-17 |
-16 |
-15 |
|
Y |
147 |
245 |
343 |
441 |
539 |
637 |
735 |
833 |
931 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
51=D1 m=1
N
|
N |
-24 |
-23 |
-22 |
-21 |
-20 |
-19 |
-18 |
-17 |
-16 |
|
Y |
153 |
255 |
357 |
459 |
561 |
663 |
765 |
867 |
969 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
N
|
N |
-28 |
-27 |
-26 |
-25 |
-24 |
-23 |
-22 |
|
Y |
177 |
295 |
413 |
531 |
649 |
767 |
885 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
61=D1 m=1
N
|
N |
-29 |
-28 |
-27 |
-26 |
-25 |
-24 |
-23 |
|
Y |
183 |
305 |
427 |
549 |
671 |
793 |
915 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
63=D1 m=1
N
|
N |
-30 |
-29 |
-28 |
-27 |
-26 |
-25 |
-24 |
|
Y |
189 |
315 |
441 |
567 |
693 |
819 |
945 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
65=D1 m=1
N
|
N |
-31 |
-30 |
-29 |
-28 |
-27 |
-26 |
-25 |
|
Y |
195 |
325 |
455 |
585 |
715 |
845 |
975 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
m=1
67=D1
N
|
N |
-32 |
-31 |
-30 |
-29 |
-28 |
-27 |
|
Y |
201 |
335 |
469 |
603 |
737 |
871 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
71=D1 m=1
N
|
N |
-34 |
-33 |
-32 |
-31 |
-30 |
-29 |
|
Y |
213 |
355 |
497 |
639 |
781 |
923 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
75=D1 m=1
|
N |
-36 |
-35 |
-34 |
-33 |
-32 |
-31 |
|
Y |
225 |
375 |
525 |
675 |
825 |
975 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
13 |
|
79=D1 m=1 N |
|||||
|
N |
-38 |
-37 |
-36 |
-35 |
-34 |
|
Y |
237 |
395 |
553 |
711 |
869 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
|
83=D1 m=1 N |
|||||
|
N |
-40 |
-39 |
-38 |
-37 |
-36 |
|
Y |
249 |
415 |
581 |
747 |
913 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
|
87=D1 m=1 N |
|||||
|
N |
-42 |
-41 |
-40 |
-39 |
-38 |
|
Y |
261 |
435 |
609 |
783 |
957 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
|
91=D1 m=1 |
|||||
N
81=D1
N
|
N |
-39 |
-38 |
-37 |
-36 |
-35 |
|
Y |
243 |
405 |
567 |
729 |
891 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
m = 1
85=D1 N
|
N |
-41 |
-40 |
-39 |
-38 |
-37 |
|
Y |
255 |
425 |
595 |
765 |
935 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
89=D1 m = 1 N
|
N |
-43 |
-42 |
-41 |
-40 |
-39 |
|
Y |
267 |
445 |
623 |
801 |
979 |
|
D2 |
3 |
5 |
7 |
9 |
11 |
|
N |
-44 |
-43 |
-42 |
-41 |
|
Y |
273 |
455 |
637 |
819 |
|
D2 |
3 |
5 |
7 |
9 |
95=D1 m=1
N
|
N |
-46 |
-45 |
-44 |
-43 |
|
Y |
285 |
475 |
665 |
855 |
|
D2 |
3 |
5 |
7 |
9 |
N
99=D1 m=1
|
N |
-48 |
-47 |
-46 |
-45 |
|
Y |
297 |
495 |
693 |
891 |
|
D2 |
3 |
5 |
7 |
9 |
|
103=D1 m=1 N |
||||
|
N |
-50 |
-49 |
-48 |
-47 |
|
Y |
309 |
515 |
721 |
927 |
|
D2 |
3 |
5 |
7 |
9 |
|
107=D1 m = 1 107=D1 N |
||||
|
N |
-52 |
-51 |
-50 |
-49 |
|
Y |
321 |
535 |
749 |
963 |
|
D2 |
3 |
5 |
7 |
9 |
|
111=D1 m = 1 111=D1 N |
||||
|
N |
-54 |
-53 |
-52 |
-51 |
|
Y |
333 |
555 |
777 |
999 |
|
D2 |
3 |
5 |
7 |
9 |
|
115=D1 m=1 N |
||||
|
N |
-56 |
-55 |
-54 |
|
|
Y |
345 |
575 |
805 |
|
|
D2 |
3 |
5 |
7 |
|
|
121=D1 m=1 N |
||||
|
N |
-59 |
-58 |
-57 |
|
|
Y |
363 |
605 |
847 |
|
|
D2 |
3 |
5 |
7 |
|
|
127=D1 m=1 N |
||||
|
N |
-62 |
-61 |
-60 |
|
|
Y |
381 |
635 |
889 |
|
|
D2 |
3 |
5 |
7 |
|
|
133=D1 m=1 N |
||||
|
N |
-65 |
-64 |
-63 |
|
|
Y |
399 |
665 |
931 |
|
|
D2 |
3 |
5 |
7 |
|
|
139=D1 m=1 N |
||||
|
N |
-68 |
-67 |
-66 |
|
|
Y |
417 |
695 |
973 |
|
|
D2 |
3 |
5 |
7 |
|
|
145=D1 m=1 N |
||||
|
N |
-71 |
-70 |
||
|
Y |
435 |
725 |
||
|
D2 |
3 |
5 |
||
|
N |
-51 |
-50 |
-49 |
-48 |
|
Y |
315 |
525 |
735 |
945 |
|
D2 |
3 |
5 |
7 |
9 |
|
m = 1 |
109=D1 N |
|||
|
N |
-53 |
-52 |
-51 |
-50 |
|
Y |
327 |
545 |
763 |
981 |
|
D2 |
3 |
5 |
7 |
9 |
|
m = 1 |
113=D1 N |
|||
|
N |
-55 |
-54 |
-53 |
|
|
Y |
339 |
565 |
791 |
|
|
D2 |
3 |
5 |
7 |
|
117=D1 m = 1
N
|
N |
-57 |
-56 |
-55 |
|
Y |
351 |
585 |
819 |
|
D2 |
3 |
5 |
7 |
123=D1 m = 1
N
|
N |
-60 |
-59 |
-58 |
|
Y |
369 |
615 |
861 |
|
D2 |
3 |
5 |
7 |
129=D1 m = 1 N
|
N |
-63 |
-62 |
-61 |
|
Y |
387 |
645 |
903 |
|
D2 |
3 |
5 |
7 |
135=D1 m = 1
N
|
N |
-66 |
-65 |
-64 |
|
Y |
405 |
675 |
945 |
|
D2 |
3 |
5 |
7 |
141=D1 m = 1
N
|
N |
-69 |
-68 |
-67 |
|
Y |
423 |
705 |
987 |
|
D2 |
3 |
5 |
7 |
147=D1 m = 1
N
|
N |
-72 |
-71 |
|
Y |
441 |
735 |
|
D2 |
3 |
5 |
119=D1 m = 1
N
|
N |
-58 |
-57 |
-56 |
|
Y |
357 |
595 |
833 |
|
D2 |
3 |
5 |
7 |
125=D1 m = 1
N
|
N |
-61 |
-60 |
-59 |
|
Y |
375 |
625 |
875 |
|
D2 |
3 |
5 |
7 |
131=D1 m = 1 N
|
N |
-64 |
-63 |
-62 |
|
Y |
393 |
655 |
917 |
|
D2 |
3 |
5 |
7 |
137=D1 m = 1 137=D1 N
|
N |
-67 |
-66 |
-65 |
|
Y |
411 |
685 |
959 |
|
D2 |
3 |
5 |
7 |
151=D1 m=1
N
|
N |
-74 |
-73 |
|
Y |
453 |
755 |
|
D2 |
3 |
5 |
157=D1 m=1
N
|
N |
-77 |
-76 |
|
Y |
471 |
785 |
|
D2 |
3 |
5 |
163=D1 m=1
N
|
N |
-80 |
-77 |
|
Y |
489 |
815 |
|
D2 |
3 |
5 |
167=D1 m = 1 167=D1 N
|
N |
-82 |
-81 |
|
Y |
501 |
835 |
|
D2 |
3 |
5 |
169=D1 m=1
N
|
N |
-83 |
-82 |
|
Y |
507 |
845 |
|
D2 |
3 |
5 |
175=D1 m = 1 175=D1 N
|
N |
-86 |
-85 |
|
Y |
525 |
875 |
|
D2 |
3 |
5 |
181=D1 m=1 N
|
N |
-89 |
-88 |
|
Y |
543 |
905 |
|
D2 |
3 |
5 |
187=D1 m=1
N
|
N |
-92 |
-91 |
|
Y |
561 |
935 |
|
D2 |
3 |
5 |
193=D1 m=1
N
|
N |
-95 |
-94 |
|
Y |
579 |
965 |
|
D2 |
3 |
5 |
199=D1 m = 1 199=D1 N
|
N |
-98 |
-97 |
|
Y |
597 |
995 |
|
D2 |
3 |
5 |
|
171=D1 m = 1 N |
||
|
N |
-84 |
-83 |
|
Y |
513 |
855 |
|
D2 |
3 |
5 |
|
177=D1 m = 1 177=D1 N |
||
|
N |
-87 |
-86 |
|
Y |
531 |
885 |
|
D2 |
3 |
5 |
|
183=D1 m = 1 N |
||
|
N |
-90 |
-89 |
|
Y |
549 |
915 |
|
D2 |
3 |
5 |
|
189=D1 m = 1 N |
||
|
N |
-93 |
-92 |
|
Y |
567 |
945 |
|
D2 |
3 |
5 |
|
195=D1 m = 1 N |
||
|
N |
-96 |
-95 |
|
Y |
585 |
975 |
|
D2 |
3 |
5 |
|
m = 1 |
201=D1 N |
|
|
N |
-99 |
|
|
Y |
603 |
|
|
D2 |
3 |
|
m = 1
173=D1
N
|
N |
-85 |
-84 |
|
Y |
519 |
865 |
|
D2 |
3 |
5 |
191=D1 N
m = 1
|
N |
-94 |
-93 |
|
Y |
573 |
955 |
|
D2 |
3 |
5 |
m = 1
197=D1
N
|
N |
-97 |
-96 |
|
Y |
591 |
985 |
|
D2 |
3 |
5 |
203=D1
N
m = 1
|
N |
-100 |
|
Y |
609 |
|
D2 |
3 |
223=D1 m=1
N
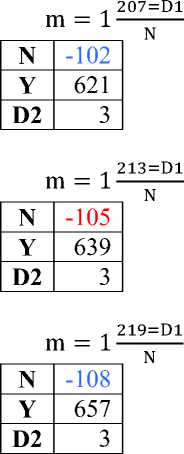
225=D1 m = 1
N
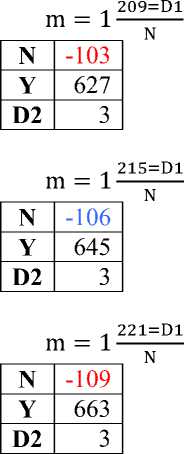
227=D1 m = 1
N
|
N |
-110 |
|
Y |
669 |
|
D2 |
3 |
|
N |
-111 |
|
Y |
675 |
|
D2 |
3 |
|
N |
-112 |
|
Y |
681 |
|
D2 |
3 |
229=D1 m=1
N
|
N |
-113 |
|
Y |
687 |
|
D2 |
3 |

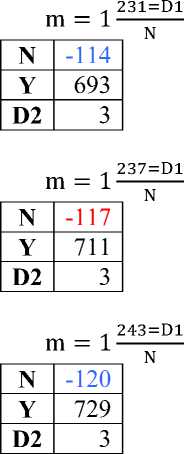
249=D1 m = 1
N
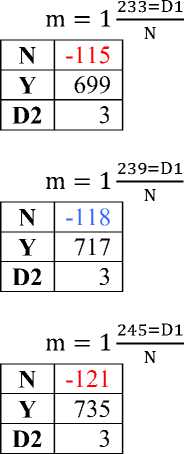

|
N |
-123 |
|
Y |
747 |
|
D2 |
3 |
255=D1 m = 1
N
|
N |
-126 |
|
Y |
765 |
|
D2 |
3 |

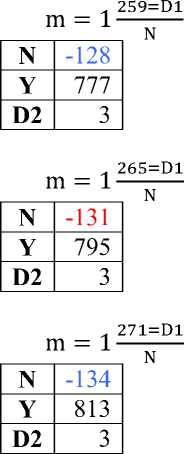
277=D1 m=1
N
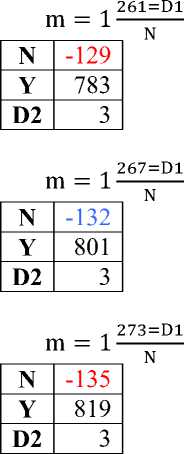
279=D1 m = 1
N
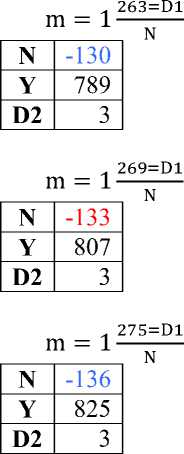
281=D1 m = 1
N
|
N |
-137 |
|
Y |
831 |
|
D2 |
3 |
|
N |
-138 |
|
Y |
837 |
|
D2 |
3 |
|
N |
-139 |
|
Y |
843 |
|
D2 |
3 |
283=D1 m=1
N
|
N |
-140 |
|
Y |
849 |
|
D2 |
3 |

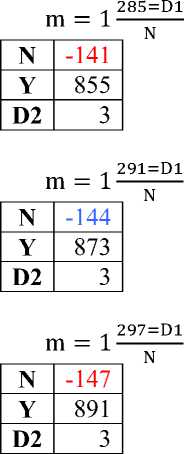
303=D1 m = 1
N
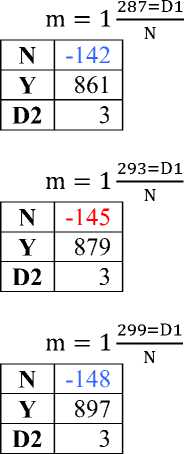
305=D1 m = 1
N

|
N |
-150 |
|
Y |
909 |
|
D2 |
3 |
|
N |
-151 |
|
Y |
915 |
|
D2 |
3 |
309=D1 m = 1
N
|
N |
-153 |
|
Y |
927 |
|
D2 |
3 |
m = 1
|
N |
-154 |
|
Y |
933 |
|
D2 |
3 |
311=D1 N
|
313=D1 m=1 N |
m = 1 3 |
15=D1 N |
m = 1 3 |
17=D1 N |
|||||||||||||||||||
|
N |
-155 |
N |
-156 |
N |
-157 |
||||||||||||||||||
|
Y |
939 |
Y |
945 |
Y |
951 |
||||||||||||||||||
|
D2 |
3 |
D2 |
3 |
D2 |
3 |
||||||||||||||||||
|
m=1 |
19=D1 N |
m = 1 3 |
21=D1 N |
323=D1 m = 1 N |
|||||||||||||||||||
|
N |
-158 |
N |
-159 |
N |
-160 |
||||||||||||||||||
|
Y |
957 |
Y |
963 |
Y |
969 |
||||||||||||||||||
|
D2 |
3 |
D2 |
3 |
D2 |
3 |
||||||||||||||||||
|
325=D1 m=1 N |
327=D1 m = 1 327=D1 N |
m = 1 3 |
29=D1 N |
||||||||||||||||||||
|
N |
-161 |
N |
-162 |
N |
-163 |
||||||||||||||||||
|
Y |
975 |
Y |
981 |
Y |
987 |
||||||||||||||||||
|
D2 |
3 |
D2 |
3 |
D2 |
3 |
||||||||||||||||||
|
331=D1 m=1 N |
m = 1 3 |
33=D1 N |
|||||||||||||||||||||
|
N |
-164 |
N |
-165 |
||||||||||||||||||||
|
Y |
993 |
Y |
999 |
||||||||||||||||||||
|
D2 |
3 |
D2 |
3 |
||||||||||||||||||||
|
m=11= |
Таблица 3. Нахождение простых чисел (до 1000). D1 N |
||||||||||||||||||||||
|
N |
1 |
2 |
3 4 5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|||||
|
Y |
3 |
5 |
7 9 11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
31 |
33 |
35 |
37 |
39 |
41 |
|||||
|
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
||||||||
|
43 |
45 |
47 |
49 |
51 |
53 |
55 |
57 |
59 |
61 |
63 |
65 |
67 |
69 |
71 |
73 |
75 |
77 |
79 |
||||||||
|
40 |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
|
81 |
83 |
85 |
87 |
89 |
91 |
93 |
95 |
97 |
99 |
101 |
103 |
105 |
107 |
109 |
111 |
113 |
|
57 |
58 59 |
60 |
61 62 63 |
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
|||||
115 117 119 121 123 125 127 129 131 133 135 137 139 141 143
|
72 |
73 |
74 |
75 |
76 |
77 |
78 |
79 |
80 |
81 |
82 |
83 |
84 |
85 |
86 |
|||||||||||||||
|
145 |
147 |
149 |
151 |
153 |
155 |
157 |
159 |
161 |
163 |
165 |
167 |
169 |
171 |
173 |
|||||||||||||||
|
87 |
88 |
89 |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
100 |
101 |
||||||||||||
|
175 |
177 |
179 |
181 |
183 |
185 |
187 |
189 |
191 |
193 |
195 |
197 |
199 |
201 |
203 |
||||||||||||
|
102 |
103 |
104 |
105 |
106 |
107 |
108 |
109 |
110 |
111 |
112 |
113 |
114 |
115 |
116 |
||||
|
205 |
207 |
209 |
211 |
213 |
215 |
217 |
219 |
221 |
223 |
225 |
227 |
229 |
231 |
233 |
||||
|
117 |
118 |
119 |
120 |
121 |
122 |
123 |
124 |
125 |
126 |
127 |
128 |
129 |
130 |
131 |
|||||
|
235 |
237 |
239 |
241 |
243 |
245 |
247 |
249 |
251 |
253 |
255 |
257 |
259 |
261 |
263 |
|||||
|
132 |
133 |
134 |
135 |
136 |
137 |
138 |
139 |
140 |
141 |
142 |
143 |
144 |
145 |
146 |
||||
|
265 |
267 |
269 |
271 |
273 |
275 |
277 |
279 |
281 |
283 |
285 |
287 |
289 |
291 |
293 |
||||
|
147 |
148 |
149 |
150 |
151 |
152 |
153 |
154 |
155 |
156 |
157 |
158 |
159 |
160 |
161 |
||||
|
295 |
297 |
299 |
301 |
303 |
305 |
307 |
309 |
311 |
313 |
315 |
317 |
319 |
321 |
323 |
||||
|
162 |
163 |
164 |
165 |
166 |
167 |
168 |
169 |
170 |
171 |
172 |
173 |
174 |
175 |
176 |
|
325 |
327 |
329 |
331 |
333 |
335 |
337 |
339 |
341 |
343 |
345 |
347 |
349 |
351 |
353 |
|
177 |
178 |
179 |
180 |
181 |
182 |
183 |
184 |
185 |
186 |
187 |
188 |
189 |
190 |
191 |
|
355 |
357 |
359 |
361 |
363 |
365 |
367 |
369 |
371 |
373 |
375 |
377 |
379 |
381 |
383 |
|
192 |
193 |
194 |
195 |
196 |
197 |
198 |
199 |
200 |
201 |
202 |
203 |
204 |
205 |
206 |
|
385 |
387 |
389 |
391 |
393 |
395 |
397 |
399 |
401 |
403 |
405 |
407 |
409 |
411 |
413 |
|
207 |
208 |
209 |
210 |
211 |
212 |
213 |
214 |
215 |
216 |
217 |
218 |
219 |
220 |
221 |
|
415 |
417 |
419 |
421 |
423 |
425 |
427 |
429 |
431 |
433 |
435 |
437 |
439 |
441 |
443 |
|
222 |
223 |
224 |
225 |
226 |
227 |
228 |
229 |
230 |
231 |
232 |
233 |
234 |
235 |
236 |
|
445 |
447 |
449 |
451 |
453 |
455 |
457 |
459 |
461 |
463 |
465 |
467 |
469 |
471 |
473 |
|
237 |
238 |
239 |
240 |
241 |
242 |
243 |
244 |
245 |
246 |
247 |
248 |
249 |
250 |
251 |
|||||
|
475 |
477 |
479 |
481 |
483 |
485 |
487 |
489 |
491 |
493 |
495 |
497 |
499 |
501 |
503 |
|||||
|
252 |
253 |
254 |
255 |
256 |
257 |
258 |
259 |
260 |
261 |
262 |
263 |
264 |
265 |
266 |
||||
|
505 |
507 |
509 |
511 |
513 |
515 |
517 |
519 |
521 |
523 |
525 |
527 |
529 |
531 |
533 |
||||
|
267 |
268 |
269 |
270 |
271 |
272 |
273 |
274 |
275 |
276 |
277 |
278 |
279 |
280 |
281 |
||||||
|
535 |
537 |
539 |
541 |
543 |
545 |
547 |
549 |
551 |
553 |
555 |
557 |
559 |
561 |
563 |
||||||
|
282 |
283 |
284 |
285 |
286 |
287 |
288 |
289 |
290 |
291 |
292 |
293 |
294 |
295 |
296 |
||||||
|
565 |
567 |
569 |
571 |
573 |
575 |
577 |
579 |
581 |
583 |
585 |
587 |
589 |
591 |
593 |
||||||
|
297 |
298 |
299 |
300 |
301 |
302 |
303 |
304 |
305 |
306 |
307 |
308 |
309 |
310 |
311 |
||||
|
595 |
597 |
599 |
601 |
603 |
605 |
607 |
609 |
611 |
613 |
615 |
617 |
619 |
621 |
623 |
||||
|
312 |
313 |
314 |
315 |
316 |
317 |
318 |
319 |
320 |
321 |
322 |
323 |
324 |
325 |
326 |
||||
|
625 |
627 |
629 |
631 |
633 |
635 |
637 |
639 |
641 |
643 |
645 |
647 |
649 |
651 |
653 |
||||
|
327 |
328 |
329 |
330 |
331 |
332 |
333 |
334 |
335 |
336 |
337 |
338 |
339 |
340 |
341 |
|
655 |
657 |
659 |
661 |
663 |
665 |
667 |
669 |
671 |
673 |
675 |
677 |
679 |
681 |
683 |
|
342 |
343 |
344 |
345 |
346 |
347 |
348 |
349 |
350 |
351 |
352 |
353 |
354 |
355 |
356 |
|
685 |
687 |
689 |
691 |
693 |
695 |
697 |
699 |
701 |
703 |
705 |
707 |
709 |
711 |
713 |
|
357 |
358 |
359 |
360 |
361 |
362 |
363 |
364 |
365 |
366 |
367 |
368 |
369 |
370 |
371 |
|
715 |
717 |
719 |
721 |
723 |
725 |
727 |
729 |
731 |
733 |
735 |
737 |
739 |
741 |
743 |
|
372 |
373 |
374 |
375 |
376 |
377 |
378 |
379 |
380 |
381 |
382 |
383 |
384 |
385 |
386 |
||||||||
|
745 |
747 |
749 |
751 |
753 |
755 |
757 |
759 |
761 |
763 |
765 |
767 |
769 |
771 |
773 |
||||||||
|
387 |
388 |
389 |
390 |
391 |
392 |
393 |
394 |
395 |
396 |
397 |
398 |
399 |
400 |
401 |
|||||
|
775 |
777 |
779 |
781 |
783 |
785 |
787 |
789 |
791 |
793 |
795 |
797 |
799 |
801 |
803 |
|||||
|
402 |
403 |
404 |
405 |
406 |
407 |
408 |
409 |
410 |
411 |
412 |
413 |
414 |
415 |
416 |
|
805 |
807 |
809 |
811 |
813 |
815 |
817 |
819 |
821 |
823 |
825 |
827 |
829 |
831 |
833 |
|
417 |
418 |
419 |
420 |
421 |
422 |
423 |
424 |
425 |
426 |
427 |
428 |
429 |
430 |
431 |
|
835 |
837 |
839 |
841 |
843 |
845 |
847 |
849 |
851 |
853 |
855 |
857 |
859 |
861 |
863 |
|
432 |
433 |
434 |
435 |
436 |
437 |
438 |
439 |
440 |
441 |
442 |
443 |
444 |
445 |
446 |
|
865 |
867 |
869 |
871 |
873 |
875 |
877 |
879 |
881 |
883 |
885 |
887 |
889 |
891 |
893 |
|
447 |
448 |
449 |
450 |
451 |
452 |
453 |
454 |
455 |
456 |
457 |
458 |
459 |
460 |
461 |
|
895 |
897 |
899 |
901 |
903 |
905 |
907 |
909 |
911 |
913 |
915 |
917 |
919 |
921 |
923 |
|
462 |
463 |
464 |
465 |
466 |
467 |
468 |
469 |
470 |
471 |
472 |
473 |
474 |
475 |
476 |
|
925 |
927 |
929 |
931 |
933 |
935 |
937 |
939 |
941 |
943 |
945 |
947 |
949 |
951 |
953 |
|
477 |
478 |
479 |
480 |
481 |
482 |
483 |
484 |
485 |
486 |
487 |
488 |
489 |
490 |
491 |
|||||
|
955 |
957 |
959 |
961 |
963 |
965 |
967 |
969 |
971 |
973 |
975 |
977 |
979 |
981 |
983 |
|||||
|
492 |
493 |
494 |
495 |
496 |
497 |
498 |
499 |
||
|
985 |
987 |
989 |
991 |
993 |
995 |
997 |
999 |
||
3=D1
m=
N
|
N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
||||||||||
|
Y |
9 |
15 |
21 |
27 |
33 |
39 |
45 |
51 |
57 |
63 |
69 |
75 |
81 |
87 |
93 |
99 |
105 |
111 |
||||||||||
|
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
||||||||||||||||||||
|
117 |
123 |
129 |
135 |
141 |
147 |
153 |
159 |
165 |
171 |
177 |
183 |
189 |
195 |
201 |
||||||||||||||||||||
|
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
||||||
|
207 |
213 |
219 |
225 |
231 |
237 |
243 |
249 |
255 |
261 |
267 |
273 |
279 |
285 |
291 |
||||||
|
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
60 |
61 |
62 |
|||||||
|
297 |
303 |
309 |
315 |
321 |
327 |
333 |
339 |
345 |
351 |
357 |
363 |
369 |
375 |
381 |
|||||||
|
63 |
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
72 |
73 |
74 |
75 |
76 |
77 |
||||||
|
387 |
393 |
399 |
405 |
411 |
417 |
423 |
429 |
435 |
441 |
447 |
453 |
459 |
465 |
471 |
||||||
|
78 |
79 |
80 |
81 |
82 |
83 |
84 |
85 |
86 |
87 |
88 |
89 |
90 |
91 |
92 |
||||||
|
477 |
483 |
489 |
495 |
501 |
507 |
513 |
519 |
525 |
531 |
537 |
543 |
549 |
555 |
561 |
||||||
|
93 |
94 |
95 |
96 |
97 |
98 |
99 |
100 |
101 |
102 |
103 |
104 |
105 |
106 |
107 |
||||||
|
567 |
573 |
579 |
585 |
591 |
597 |
603 |
609 |
615 |
621 |
627 |
633 |
639 |
645 |
651 |
||||||
|
108 |
109 |
110 |
111 |
112 |
113 |
114 |
115 |
116 |
117 |
118 |
119 |
120 |
121 |
122 |
|
657 |
663 |
669 |
675 |
681 |
687 |
693 |
699 |
705 |
711 |
717 |
723 |
729 |
735 |
741 |
|
123 |
124 |
125 |
126 |
127 |
128 |
129 |
130 |
131 |
132 |
133 |
134 |
135 |
136 |
137 |
|
747 |
753 |
759 |
765 |
771 |
777 |
783 |
789 |
795 |
801 |
807 |
813 |
819 |
825 |
831 |
|
138 |
139 |
140 |
141 |
142 |
143 |
144 |
145 |
146 |
147 |
148 |
149 |
150 |
151 |
152 |
|
837 |
843 |
849 |
855 |
861 |
867 |
873 |
879 |
885 |
891 |
897 |
903 |
909 |
915 |
921 |
|
153 |
154 |
155 |
156 |
157 |
158 |
159 |
160 |
161 |
162 |
163 |
164 |
165 |
||||||
|
927 |
933 |
939 |
945 |
951 |
957 |
963 |
969 |
975 |
981 |
987 |
993 |
999 |
||||||
|
5=D1 m=1 N |
||||||||||||||||||
|
N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
||
|
Y |
25 |
35 |
45 |
55 |
65 |
75 |
85 |
95 |
105 |
115 |
125 |
135 |
145 |
155 |
165 |
175 |
||
|
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
||||
|
185 |
195 |
205 |
215 |
225 |
235 |
245 |
255 |
265 |
275 |
285 |
295 |
305 |
315 |
325 |
||||
|
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
||||
|
335 |
345 |
355 |
365 |
375 |
385 |
395 |
405 |
415 |
425 |
435 |
445 |
455 |
465 |
475 |
||||
|
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
60 |
||||
|
485 |
495 |
505 |
515 |
525 |
535 |
545 |
555 |
565 |
575 |
585 |
595 |
605 |
615 |
625 |
||||
|
61 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
72 |
73 |
74 |
75 |
||||
|
635 |
645 |
655 |
665 |
675 |
685 |
695 |
705 |
715 |
725 |
735 |
745 |
755 |
765 |
775 |
||||
|
76 |
77 |
78 |
79 |
80 |
81 |
82 |
83 |
84 |
85 |
86 |
87 |
88 |
89 |
90 |
||||
|
785 |
795 |
805 |
815 |
825 |
835 |
845 |
855 |
865 |
875 |
885 |
895 |
905 |
915 |
925 |
||||
|
91 |
92 |
93 |
94 |
95 |
96 |
97 |
||||||||||||
|
935 |
945 |
955 |
965 |
975 |
985 |
995 |
||||||||||||
|
7=D1 m = 1 7=D1 N |
||||||||||||||||||
|
N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|||
|
Y |
49 |
63 |
77 |
91 |
105 |
119 |
133 |
147 |
161 |
175 |
189 |
203 |
217 |
231 |
245 |
|||
|
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
||||
|
259 |
273 |
287 |
301 |
315 |
329 |
343 |
357 |
371 |
385 |
399 |
413 |
427 |
441 |
455 |
||||
|
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
||||
|
469 |
483 |
497 |
511 |
525 |
539 |
553 |
567 |
581 |
595 |
609 |
623 |
637 |
651 |
665 |
||||
|
45 |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
||||
|
679 |
693 |
707 |
721 |
735 |
749 |
763 |
777 |
791 |
805 |
819 |
833 |
847 |
861 |
875 |
||||
|
60 |
61 |
62 |
63 |
64 |
65 |
66 |
67 |
||
|
889 |
903 |
917 |
931 |
945 |
959 |
973 |
987 |
||
891 909 927 945 963 981 999
11=D1 m=1
N
N
Y 121
143 165 187 209 231 253 275 297 319 341 363 385 407 429
|
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
|
451 |
473 |
495 |
517 |
539 |
561 |
583 |
605 |
627 |
649 |
671 |
693 |
715 |
737 |
759 |
|
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
|
781 |
803 |
825 |
847 |
869 |
891 |
913 |
935 |
957 |
979 |
13=D1 m=1
N
|
N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
Y |
169 |
195 |
221 |
247 |
273 |
299 |
325 |
351 |
377 |
403 |
429 |
455 |
481 |
507 |
533 |
|
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
|
559 |
585 |
611 |
637 |
663 |
689 |
715 |
741 |
767 |
793 |
819 |
845 |
871 |
897 |
923 |
|
30 |
31 |
|
949 |
975 |
15=D1 m=1
N
|
N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
Y |
225 |
255 |
285 |
315 |
345 |
375 |
405 |
435 |
465 |
495 |
525 |
555 |
585 |
615 |
645 |
|
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
675 |
705 |
735 |
765 |
795 |
825 |
855 |
885 |
915 |
945 |
975 |
17=D1 m=1
N
|
N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
Y |
289 |
323 |
357 |
391 |
425 |
459 |
493 |
527 |
561 |
595 |
629 |
663 |
697 |
731 |
765 |
|
15 |
16 |
17 |
18 |
19 |
20 |
|
|
799 |
833 |
867 |
901 |
935 |
969 |
|
19=D1 m=1
N
N
Y 361 399 437 475 513 551 589 627 665 703 741 779 817 855
|
14 |
15 |
16 |
|
893 |
931 |
969 |
21=D1 m = 1 21=D1 N
|
N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
Y |
441 |
483 |
525 |
567 |
609 |
651 |
693 |
735 |
777 |
819 |
861 |
903 |
945 |
987 |
23=D1 m=1
N
|
N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Y |
529 |
575 |
621 |
667 |
713 |
759 |
805 |
851 |
897 |
943 |
989 |
25=D1 m=1
N
|
N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Y |
625 |
675 |
725 |
775 |
825 |
875 |
925 |
975 |
27=D1 m=1
N
|
N |
0 |
1 |
2 |
3 |
4 |
5 |
|
Y |
729 |
783 |
837 |
891 |
945 |
999 |
29=D1 m=1
N
|
N |
0 |
1 |
2 |
|
Y |
841 |
899 |
957 |
|
m=1 |
31=D1 N |
||
|
N |
0 |
||
|
Y |
961 |
||
Таблица 3.1. Сводная таблица из Таблицы 3.
|
данные из Таблицы 3: N / Y \ D1, для проверки √N 2 + Y = N + D1 |
||||||||
|
∑ = 1 |
∑ = 3 |
∑ = 5 |
∑ = 7 |
∑ = 9 |
∑ = 2 |
∑ = 4 |
∑ = 6 |
∑ = 8 |
|
0/ 1 \1 |
-1/3\3 |
2/ 5 \1 |
3/ 7 \1 |
0/9\3 |
5/ 11 \1 |
6/ 13 \1 |
1/15\3 |
8/ 17 \1 |
|
9/ 19 \1 |
2/21\3 |
11/ 23 \1 |
0/25 \5 |
3/27\3 |
14/ 29 \1 |
15/ 31 \1 |
4/33\3 |
1/35 \5 |
|
18/ 37 \1 |
5/39\3 |
20/ 41 \1 |
21/ 43 \1 |
6/45\3 |
23/ 47 \1 |
0/49 \7 |
7/51\3 |
26/ 53\1 |
|
3/55 \5 |
8/57\3 |
29 /59\ 1 |
30/ 61 \1 |
9/63\3 |
4/65 \5 |
33/ 67 \1 |
10/69\3 |
35/ 71 \1 |
|
36/ 73 \1 |
11/75\3 |
2/77 \7 |
39/ 79 \1 |
12/81\3 |
41/ 83 \1 |
6/85 \5 |
13/87\3 |
44/ 89 \1 |
|
3/91 \7 |
14/93\3 |
7/95 \5 |
48/ 97 \1 |
15/99\3 |
50/ 101 \1 |
51/ 103 \1 |
16/105\3 |
53/ 107 \1 |
|
54/ 109 \1 |
17/111\3 |
56/ 113 \1 |
9/115 \5 |
18/117\3 |
5/119 \7 |
0/121 \11 |
19/123\3 |
10/125\5 |
|
63/ 127 \1 |
20/129\3 |
65/ 131 \1 |
6/133 \7 |
21/135\3 |
68/ 137 \1 |
69/ 139 \1 |
22/141\3 |
1/143 \11 |
|
12/145\5 |
23/147\3 |
74/ 149 \1 |
75/ 151 \1 |
24/153\3 |
13/155\5 |
78/ 157 \1 |
25/159\3 |
8/161 \7 |
|
81/ 163 \1 |
26/165\3 |
83/ 167 \1 |
0/169 \13 |
27/171\3 |
86/ 173 \1 |
15/175\5 |
28/177\3 |
89/ 179 \1 |
|
90/ 181 \1 |
29/183\3 |
16/185\5 |
3/187 \11 |
30/189\3 |
95/ 191 \1 |
96/ 193 \1 |
31/195\3 |
98/ 197 \1 |
|
99/ 199 \1 |
32/201\3 |
11/203 \7 |
18/205\5 |
33/207\3 |
4/209 \11 |
105/ 211 \1 |
34/213\3 |
19/215\5 |
|
12/217 \7 |
35/219\3 |
2/221 \13 |
111/ 223 \1 |
36/225\3 |
113/ 227 \1 |
114/ 229 \1 |
37/231\3 |
116/ 233 \1 |
|
21/235\5 |
38/237\3 |
119/239\1 |
120/241\1 |
39/243\3 |
22/245\5 |
3/247 \13 |
40/249\3 |
125/251\1 |
|
6/253 \11 |
41/255\3 |
128/257\1 |
15/259 \7 |
42/261\3 |
131/263\1 |
24/265\5 |
43/267\3 |
134/269\1 |
|
135/271\1 |
44/273\3 |
25/275\5 |
138/277\1 |
45/279\3 |
140/281\1 |
141/283\1 |
46/285\3 |
17/287 \7 |
|
0/289 \17 |
47/291\3 |
146/293\1 |
27/295\5 |
48/297\3 |
5/299 \13 |
18/301 \7 |
49/303\3 |
28/305\5 |
|
153/307\1 |
50/309\3 |
155/311\1 |
156/313\1 |
51/315\3 |
158/317\1 |
9/319 \11 |
52/321\3 |
1/323 \17 |
|
30/325\5 |
53/327\3 |
20/329 \7 |
165/331\1 |
54/333\3 |
31/335\5 |
168/3371 |
55/339\3 |
10/341\1 |
|
21/343 \7 |
56/345\3 |
173/347\1 |
174/349\1 |
57/351\3 |
176/353\1 |
33/355\5 |
58/357\3 |
179/359\1 |
|
0/361 \19 |
59/363\3 |
34/365\5 |
183/367\1 |
60/369\3 |
23/371 \7 |
186/373\1 |
61/375\3 |
8/377 \13 |
|
189/379\1 |
62/381\3 |
191/383\1 |
36/385\5 |
63/387\3 |
194/ 389 \1 |
3/391 \17 |
64/393\3 |
37/395 \5 |
|
198/ 397 \1 |
65/399\3 |
200/ 401 \1 |
9/403 \13 |
66/405\3 |
13/407\11 |
204/ 409 \1 |
67/411\3 |
26/413 \7 |
|
39/415 \5 |
68/417\3 |
209/ 419 \1 |
210/ 421 \1 |
69/423\3 |
40/425 \5 |
27/427 \7 |
70/429\3 |
215/ 431 \1 |
|
216/ 433 \1 |
71/435\3 |
2/437 \19 |
219/ 439 \1 |
72/441\3 |
221/ 443 \1 |
42/445 \5 |
73/447\3 |
224/ 449 \1 |
|
15/451\11 |
74/453\3 |
43/455 \5 |
228/ 457 \1 |
75/459\3 |
230/ 461 \1 |
231/ 463 \1 |
76/465\3 |
233/ 467 \1 |
|
30/469 \7 |
77/471\3 |
16/473\11 |
45/475 \5 |
78/477\3 |
239/ 479 \1 |
12/481\13 |
79/483\3 |
46/485 \5 |
|
243/ 487 \1 |
80/489\3 |
245/ 491 \1 |
6/493 \17 |
81/495\3 |
32/497 \7 |
249/ 499 \1 |
82/501\3 |
251/ 503 \1 |
|
48/505 \5 |
83/507\3 |
254/ 509 \1 |
33/511 \7 |
84/513\3 |
49/515 \5 |
18/517\11 |
85/519\3 |
260/ 521 \1 |
|
261/ 523 \1 |
86/525\3 |
7/527 \17 |
0/529 \23 |
87/531\3 |
14/533\13 |
51/535 \5 |
88/537\3 |
35/539 \7 |
|
270/ 541 \1 |
89/543\3 |
52/545 \5 |
273/ 547 \1 |
90/549\3 |
5/551 \19 |
14/553\13 |
91/555\3 |
278/ 557 \1 |
|
15/559\13 |
92/561\3 |
281/ 563 \1 |
54/565 \5 |
93/567\3 |
284/ 569 \1 |
285/ 571 \1 |
94/573\3 |
55/575 \5 |
|
288/ 577 \1 |
95/579\3 |
38/581 \7 |
21/583\11 |
96/585\3 |
293/ 587 \1 |
6/589 \19 |
97/591\3 |
296/ 593 \1 |
|
57/595 \5 |
98/597\3 |
299/ 599 \1 |
300/ 601 \1 |
99/603\3 |
58/605 \5 |
303/ 607 \1 |
100/609\3 |
17/611\13 |
|
306/ 613 \1 |
101/615\3 |
308/ 617 \1 |
309/ 619 \1 |
102/621\3 |
41/623 \7 |
60/625 \5 |
103/627\3 |
10/629\17 |
|
315/ 631 \1 |
104/633\3 |
61/635 \5 |
18/637\13 |
105/639\3 |
320/ 641 \1 |
321/ 643 \1 |
106/645\3 |
323/ 647 \1 |
|
24/649\11 |
107/651\3 |
326/ 653 \1 |
63/655 \5 |
108/657\3 |
329/ 659 \1 |
330/ 661 \1 |
109/663\3 |
64/665 \5 |
|
3/667 \23 |
110/669\3 |
25/671\11 |
336/ 673 \1 |
111/675\3 |
338/ 677 \1 |
45/679 \7 |
112/681\3 |
341/ 683 \1 |
|
66/685 \5 |
113/687\3 |
20/689\13 |
345/ 691 \1 |
114/693\3 |
67/695 \5 |
12/697\17 |
115/699\3 |
350/ 701 \1 |
|
9/703 \19 |
116/705\3 |
47/707 \7 |
354/ 709 \1 |
117/711\3 |
4/713\23 |
69/715 \5 |
118/717\3 |
359/ 719 \1 |
|
48/721 \7 |
119/723\3 |
70/725 \5 |
363/ 727 \1 |
120/729\3 |
13/731\17 |
366/ 733 \1 |
121/735\3 |
28/737\11 |
|
369/ 739 \1 |
122/741\3 |
371/ 743 \1 |
72/745 \5 |
123/747\3 |
50/749 \7 |
375/ 751 \1 |
124/753\3 |
73/755 \5 |
|
378/ 757 \1 |
125/759\3 |
380/ 761 \1 |
51/763 \7 |
126/765\3 |
23/767\13 |
384/ 769 \1 |
127/771\3 |
386/ 773 \1 |
|
75/775 \5 |
128/777\3 |
11/779\19 |
30/781\11 |
129/783\3 |
76/785 \5 |
393/ 787 \1 |
130/799\3 |
53/791 \7 |
|
24/793\13 |
131/795\3 |
398/ 797 \1 |
15/799\17 |
132/801\3 |
31/803\11 |
78/805 \5 |
133/807\3 |
404/ 809 \1 |
|
405/ 811 \1 |
134/813\3 |
79/815 \5 |
12/817\19 |
135/819\3 |
410/ 821 \1 |
411/ 823 \1 |
136/825\3 |
413/ 827 \1 |
|
414/ 829 \1 |
137/831\3 |
56/833 \7 |
81/835 \5 |
138/837\3 |
419/ 839 \1 |
0/841 \29 |
139/843\3 |
82/845 \5 |
|
57/847 \7 |
140/849\3 |
7/851 \23 |
426/ 853 \1 |
141/855\3 |
428/ 857 \1 |
429/ 859 \1 |
142/861\3 |
431/ 863 \1 |
|
84/865 \5 |
143/867\3 |
34/869\11 |
27/871\13 |
144/873\3 |
85/875 \5 |
438/ 877 \1 |
145/879\3 |
440/ 881 \1 |
|
441/ 883 \1 |
146/885\3 |
443/ 887 \1 |
60/889 \7 |
147/891\3 |
14/893\19 |
87/895 \5 |
148/897\3 |
1/899 \29 |
|
18/901\17 |
149/903\3 |
88/905 \5 |
453/ 907 \1 |
150/909\3 |
455/ 911 \1 |
36/913\11 |
151/915\3 |
62/917 \7 |
|
459/ 919 \1 |
152/921\3 |
29/923\13 |
90/925 \5 |
153/927\3 |
464/ 929 \1 |
63/931 \7 |
154/933\3 |
91/935 \5 |
|
468/ 937 \1 |
155/939\3 |
470/ 941 \1 |
9/943 \23 |
156/945\3 |
473/ 947 \1 |
30/949\13 |
157/951\3 |
476/ 953 \1 |
|
93/955 \5 |
158/957\3 |
65/959 \7 |
0/961 \31 |
159/963\3 |
94/965 \5 |
483/ 967 \1 |
160/969\3 |
485/ 971 \1 |
|
66/973 \7 |
161/975\3 |
488/ 977 \1 |
39/979\11 |
162/981\3 |
491/ 983 \1 |
96/985 \5 |
163/987\3 |
10/989\23 |
|
495/ 991 \1 |
164/993\3 |
97/995 \5 |
498/ 997 \1 |
165/999\3 |
Таблица 3.2. Правленая сводная таблица из Таблицы 3.1.
|
данные из Таблицы 3: N / Y \ D1, для проверки √ N2 + Y = N + D1 |
|||||
|
∑ = 1 |
∑ = 5 |
∑ = 7 |
∑ = 2 |
∑ = 4 |
∑ = 8 |
|
0/ 1 \1 |
2/ 5 \1 |
3/ 7 \1 |
5/ 11 \1 |
6/ 13 \1 |
8/ 17 \1 |
|
9/ 19 \1 |
11/ 23 \1 |
0/25 \5 |
14/ 29 \1 |
15/ 31 \1 |
1/35 \5 |
|
18/ 37 \1 |
20/ 41 \1 |
21/ 43 \1 |
23/ 47 \1 |
0/49 \7 |
26/ 53\1 |
|
3/55 \5 |
29 /59\ 1 |
30/ 61 \1 |
4/65 \5 |
33/ 67 \1 |
35/ 71 \1 |
|
36/ 73 \1 |
2/77 \7 |
39/ 79 \1 |
41/ 83 \1 |
6/85 \5 |
44/ 89 \1 |
|
3/91 \7 |
7/95 \5 |
48/ 97 \1 |
50/ 101 \1 |
51/ 103 \1 |
53/ 107 \1 |
|
54/ 109 \1 |
56/ 113 \1 |
9/115 \5 |
5/119 \7 |
0/121 \11 |
10/125 \5 |
|
63/ 127 \1 |
65/ 131 \1 |
6/133 \7 |
68/ 137 \1 |
69/ 139 \1 |
1/143 \11 |
|
12/145 \5 |
74/ 149 \1 |
75/ 151 \1 |
13/155 \5 |
78/ 157 \1 |
8/161 \7 |
|
81/ 163 \1 |
83/ 167 \1 |
0/169 \13 |
86/ 173 \1 |
15/175 \5 |
89/ 179 \1 |
|
90/ 181 \1 |
16/185 \5 |
3/187 \11 |
95/ 191 \1 |
96/ 193 \1 |
98/ 197 \1 |
|
99/ 199 \1 |
11/203 \7 |
18/205 \5 |
4/209 \11 |
105/ 211 \1 |
19/215 \5 |
|
12/217 \7 |
2/221 \13 |
111/ 223 \1 |
113/ 227 \1 |
114/ 229 \1 |
116/ 233 \1 |
|
21/235 \5 |
119/ 239 \1 |
120/ 241 \1 |
22/245 \5 |
3/247 \13 |
125/ 251 \1 |
|
6/253 \11 |
128/ 257 \1 |
15/259 \7 |
131/ 263 \1 |
24/265 \5 |
134/ 269 \1 |
|
135/ 271 \1 |
25/275 \5 |
138/ 277 \1 |
140/ 281 \1 |
141/ 283 \1 |
17/287 \7 |
|
0/289 \17 |
146/ 293 \1 |
27/295 \5 |
5/299 \13 |
18/301 \7 |
28/305 \5 |
|
153/ 307 \1 |
155/ 311 \1 |
156/ 313 \1 |
158/ 317 \1 |
9/319 \11 |
1/323 \17 |
|
30/325 \5 |
20/329 \7 |
165/ 331 \1 |
31/335 \5 |
168/ 337 \1 |
10/341\11 |
|
21/343 \7 |
173/ 347 \1 |
174/ 349 \1 |
176/ 353 \1 |
33/355 \5 |
179/ 359 \1 |
|
0/361 \19 |
34/365 \5 |
183/ 367 \1 |
23/371 \7 |
186/ 373 \1 |
8/377 \13 |
|
189/ 379 \1 |
191/ 383 \1 |
36/385 \5 |
194/ 389 \1 |
3/391 \17 |
37/395 \5 |
|
198/ 397 \1 |
200/ 401 \1 |
9/403 \13 |
13/407\11 |
204/ 409 \1 |
26/413 \7 |
|
39/415 \5 |
209/ 419 \1 |
210/ 421 \1 |
40/425 \5 |
27/427 \7 |
215/ 431 \1 |
|
216/ 433 \1 |
2/437 \19 |
219/ 439 \1 |
221/ 443 \1 |
42/445 \5 |
224/ 449 \1 |
|
15/451\11 |
43/455 \5 |
228/ 457 \1 |
230/ 461 \1 |
231/ 463 \1 |
233/ 467 \1 |
|
30/469 \7 |
16/473\11 |
45/475 \5 |
239/ 479 \1 |
12/481\13 |
46/485 \5 |
|
243/ 487 \1 |
245/ 491 \1 |
6/493 \17 |
32/497 \7 |
249/ 499 \1 |
251/ 503 \1 |
|
48/505 \5 |
254/ 509 \1 |
33/511 \7 |
49/515 \5 |
18/517\11 |
260/ 521 \1 |
|
261/ 523 \1 |
7/527 \17 |
0/529 \23 |
14/533\13 |
51/535 \5 |
35/539 \7 |
|
270/ 541 \1 |
52/545 \5 |
273/ 547 \1 |
5/551 \19 |
14/553\13 |
278/ 557 \1 |
|
15/559\13 |
281/ 563 \1 |
54/565 \5 |
284/ 569 \1 |
285/ 571 \1 |
55/575 \5 |
|
288/ 577 \1 |
38/581 \7 |
21/583\11 |
293/ 587 \1 |
6/589 \19 |
296/ 593 \1 |
|
57/595 \5 |
299/ 599 \1 |
300/ 601 \1 |
58/605 \5 |
303/ 607 \1 |
17/611\13 |
|
306/ 613 \1 |
308/ 617 \1 |
309/ 619 \1 |
41/623 \7 |
60/625 \5 |
10/629\17 |
|
315/ 631 \1 |
61/635 \5 |
18/637\13 |
320/ 641 \1 |
321/ 643 \1 |
323/ 647 \1 |
|
24/649\11 |
326/ 653 \1 |
63/655 \5 |
329/ 659 \1 |
330/ 661 \1 |
64/665 \5 |
|
3/667 \23 |
25/671\11 |
336/ 673 \1 |
338/ 677 \1 |
45/679 \7 |
341/ 683 \1 |
|
66/685 \5 |
20/689\13 |
345/ 691 \1 |
67/695 \5 |
12/697\17 |
350/ 701 \1 |
|
9/703 \19 |
47/707 \7 |
354/ 709 \1 |
4/713\23 |
69/715 \5 |
359/ 719 \1 |
|
48/721 \7 |
70/725 \5 |
363/ 727 \1 |
13/731\17 |
366/ 733 \1 |
28/737\11 |
|
369/ 739 \1 |
371/ 743 \1 |
72/745 \5 |
50/749 \7 |
375/ 751 \1 |
73/755 \5 |
|
378/ 757 \1 |
380/ 761 \1 |
51/763 \7 |
23/767\13 |
384/ 769 \1 |
386/ 773 \1 |
|
75/775 \5 |
11/779\19 |
30/781\11 |
76/785 \5 |
393/ 787 \1 |
53/791 \7 |
|
24/793\13 |
398/ 797 \1 |
15/799\17 |
31/803\11 |
78/805 \5 |
404/ 809 \1 |
|
405/ 811 \1 |
79/815 \5 |
12/817\19 |
410/ 821 \1 |
411/ 823 \1 |
413/ 827 \1 |
|
414/ 829 \1 |
56/833 \7 |
81/835 \5 |
419/ 839 \1 |
0/841 \29 |
82/845 \5 |
|
57/847 \7 |
7/851 \23 |
426/ 853 \1 |
428/ 857 \1 |
429/ 859 \1 |
431/ 863 \1 |
|
84/865 \5 |
34/869\11 |
27/871\13 |
85/875 \5 |
438/ 877 \1 |
440/ 881 \1 |
|
441/ 883 \1 |
443/ 887 \1 |
60/889 \7 |
14/893\19 |
87/895 \5 |
1/899 \29 |
|
18/901\17 |
88/905 \5 |
453/ 907 \1 |
455/ 911 \1 |
36/913\11 |
62/917 \7 |
|
459/ 919 \1 |
29/923\13 |
90/925 \5 |
464/ 929 \1 |
63/931 \7 |
91/935 \5 |
|
468/ 937 \1 |
470/ 941 \1 |
9/943 \23 |
473/ 947 \1 |
30/949\13 |
476/ 953 \1 |
|
93/955 \5 |
65/959 \7 |
0/961 \31 |
94/965 \5 |
483/ 967 \1 |
485/ 971 \1 |
|
66/973 \7 |
488/ 977 \1 |
39/979\11 |
491/ 983 \1 |
96/985 \5 |
10/989\23 |
|
495/ 991 \1 |
97/995 \5 |
498/ 997 \1 |
|||
Таблица 3.3. Простые и некоторые составные числа (до 1000).
|
∑ = 1 |
∑ = |
5 |
∑ = |
7 |
∑ = 2 |
∑ = |
4 |
∑ = |
8 |
Код строки |
№ дома |
|
1 |
5 |
7 |
11 |
13 |
17 |
1 5 7 1 3 7 |
|||||
|
19 |
23 |
25 |
29 |
31 |
35 |
9 3 5 9 1 5 |
|||||
|
37 |
41 |
43 |
47 |
49 |
53 |
7 1 3 7 9 3 |
1 |
||||
|
55 |
59 |
61 |
65 |
67 |
71 |
5 9 1 5 7 1 |
|||||
|
73 |
77 |
79 |
83 |
85 |
89 |
3 7 9 3 5 9 |
|||||
|
91 |
95 |
97 |
101 |
103 |
107 |
1 5 7 1 3 7 |
|||||
|
109 |
113 |
115 |
119 |
121 |
125 |
9 3 5 9 1 5 |
|||||
|
127 |
131 |
133 |
137 |
139 |
143 |
7 1 3 7 9 3 |
2 |
||||
|
145 |
149 |
151 |
155 |
157 |
161 |
5 9 1 5 7 1 |
|||||
|
163 |
167 |
169 |
173 |
175 |
179 |
3 7 9 3 5 9 |
|||||
|
181 |
185 |
187 |
191 |
193 |
197 |
1 5 7 1 3 7 |
|||||
|
199 |
203 |
205 |
209 |
211 |
215 |
9 3 5 9 1 5 |
|||||
|
217 |
221 |
223 |
227 |
229 |
233 |
7 1 3 7 9 3 |
3 |
||||
|
235 |
239 |
241 |
245 |
247 |
251 |
5 9 1 5 7 1 |
|||||
|
253 |
257 |
259 |
263 |
265 |
269 |
3 7 9 3 5 9 |
|||||
|
271 |
275 |
277 |
281 |
283 |
287 |
1 5 7 1 3 7 |
|||||
|
289 |
293 |
295 |
299 |
301 |
305 |
9 3 5 9 1 5 |
|||||
|
307 |
311 |
313 |
317 |
319 |
323 |
7 1 3 7 9 3 |
4 |
||||
|
325 |
329 |
331 |
335 |
337 |
341 |
5 9 1 5 7 1 |
|||||
|
343 |
347 |
349 |
353 |
355 |
359 |
3 7 9 3 5 9 |
|||||
|
361 |
365 |
367 |
371 |
373 |
377 |
1 5 7 1 3 7 |
|||||
|
379 |
383 |
385 |
389 |
391 |
395 |
9 3 5 9 1 5 |
|||||
|
397 |
401 |
403 |
407 |
409 |
413 |
7 1 3 7 9 3 |
5 |
||||
|
415 |
419 |
421 |
425 |
427 |
431 |
5 9 1 5 7 1 |
|||||
|
433 |
437 |
439 |
443 |
445 |
449 |
3 7 9 3 5 9 |
|||||
|
451 |
455 |
457 |
461 |
463 |
467 |
1 5 7 1 3 7 |
|||||
|
469 |
473 |
475 |
479 |
481 |
485 |
9 3 5 9 1 5 |
|||||
|
487 |
491 |
493 |
497 |
499 |
503 |
7 1 3 7 9 3 |
6 |
||||
|
505 |
509 |
511 |
515 |
517 |
521 |
5 9 1 5 7 1 |
|||||
|
523 |
527 |
529 |
533 |
535 |
539 |
3 7 9 3 5 9 |
|||||
|
541 |
545 |
547 |
551 |
553 |
557 |
1 5 7 1 3 7 |
|||||
|
559 |
563 |
565 |
569 |
571 |
575 |
9 3 5 9 1 5 |
|||||
|
577 |
581 |
583 |
587 |
589 |
593 |
7 1 3 7 9 3 |
7 |
||||
|
595 |
599 |
601 |
605 |
607 |
611 |
5 9 1 5 7 1 |
|||||
|
613 |
617 |
619 |
623 |
625 |
629 |
3 7 9 3 5 9 |
|||||
|
631 |
635 |
637 |
641 |
643 |
647 |
1 5 7 1 3 7 |
|||||
|
649 |
653 |
655 |
659 |
661 |
665 |
9 3 5 9 1 5 |
|||||
|
667 |
671 |
673 |
677 |
679 |
683 |
7 1 3 7 9 3 |
8 |
||||||
|
685 |
689 |
691 |
695 |
697 |
701 |
5 9 1 5 7 1 |
|||||||
|
703 |
707 |
709 |
713 |
715 |
719 |
3 7 9 3 5 9 |
|||||||
|
721 |
725 |
727 |
731 |
733 |
737 |
1 5 7 1 3 7 |
9 |
||||||
|
739 |
743 |
745 |
749 |
751 |
755 |
9 3 5 9 1 5 |
|||||||
|
757 |
761 |
763 |
767 |
769 |
773 |
7 1 3 7 9 3 |
|||||||
|
775 |
779 |
781 |
785 |
787 |
791 |
5 9 1 5 7 1 |
|||||||
|
793 |
797 |
799 |
803 |
805 |
809 |
3 7 9 3 5 9 |
|||||||
|
811 |
815 |
817 |
821 |
823 |
827 |
1 5 7 1 3 7 |
10 |
||||||
|
829 |
833 |
835 |
839 |
841 |
845 |
9 3 5 9 1 5 |
|||||||
|
847 |
851 |
853 |
857 |
859 |
863 |
7 1 3 7 9 3 |
|||||||
|
865 |
869 |
871 |
875 |
877 |
881 |
5 9 1 5 7 1 |
|||||||
|
883 |
887 |
889 |
893 |
895 |
899 |
3 7 9 3 5 9 |
|||||||
|
901 |
905 |
907 |
911 |
913 |
917 |
1 5 7 1 3 7 |
11 |
||||||
|
919 |
923 |
925 |
929 |
931 |
935 |
9 3 5 9 1 5 |
|||||||
|
937 |
941 |
943 |
947 |
949 |
953 |
7 1 3 7 9 3 |
|||||||
|
955 |
959 |
961 |
965 |
967 |
971 |
5 9 1 5 7 1 |
|||||||
|
973 |
977 |
979 |
983 |
985 |
989 |
3 7 9 3 5 9 |
|||||||
|
991 |
995 |
997 |
1 5 7 1 3 7 |
12 |
|||||||||
Список литературы Теория делимости и простые числа
- Дорофеева А.В. Страницы истории на уроках математики.- Квантор.1991
- Дон Цагер. Первые 50 миллионов простых чисел.- У.М.Н. 1984 г. ноябрь - декабрь.т. 39, вып. 6(240)
- Грибанов В.У., Титов П.И. Сборник упражнений по теории чисел. Просвещение.1964


