Теория движения Луны (Лунные циклы)

Попытки создания теории движения Луны не прекращаются со времён И. Ньютона. Теория движения Луны, учитывающая влияние Земли, Солнца и других планет оказалась одной из самых сложных задач астрономии. В статье представлена физическая модель движения Луны, построенная на положениях «Полного закона движения объектов в составе систем планетарного типа» [4].

Показано, что движение Луны формируется сложным сочетанием действия гравитационных составляющих притяжения Земли и Солнца, действующих на Луну в направлении движения планетарной системы. Выполнен расчёт движения Луны в соответствии с представленной физической моделью. Результаты расчёта движения Луны при взаимодействии Земли, Солнца и Луны, согласуются с наблюдаемым движением и подтверждают представленную теорию движения Луны . В расчёт может быть включено любое количество объектов (планет), оказывающих влияние на движение Луны. Результаты расчёта верифицируют «Полный закон движения объектов в составе систем планетарного типа» [4].

Оглавление

Вступление (современные представления) Теория движения Луны Вывод

Литература

Вступление (современные представления)

Движение Луны вокруг Земли представляется сегодня как сочетание нескольких движений:

• -    обращение вокруг Земли по эллиптической орбите,

• -    поворот плоскости лунной орбиты, её узлы смещаются на запад, делая полный оборот за 18,6 лет,

• -    поворот большой оси лунной орбиты с периодом 8,8 лет, (происходит в противоположном направлении, чем движение узлов),

• -    периодические изменения наклона лунной орбиты по отношению к эклиптике от 9 ⁰ 59’ до 5 ⁰ 19’,

• -    периодическое изменение размеров лунной орбиты: перигея от 356,41 до 369,96 тыс. км, апогея от 404,18 до 406,74 тыс. км,

• -    постепенное движение Луны от Земли вследствие приливного ускорения (примерно 4 см в год).

Некоторые исследователи добавляют в этот список ещё ряд движений.

Вследствие того, что каждый элемент орбиты испытывает множество возмущений с разными периодами и амплитудами, действительное движение Луны необычайно сложно, и его исследование составляет одну из самых сложных задач небесной механики [1].

В расчётах движения Луны используются выражения с десятками тысяч членов (коэффициентов и аргументов при тригонометрических функциях) и не существует предела их количеству, если требуется ещё более высокая точность.

Теория движения Луны

Перечисленные выше движения Луны не являются самостоятельными движениями, сочетания которых определяет (формирует) итоговое движение Луны. Эти движения сами являются результатом действия скрытых, сегодня не познанных взаимодействий.

В предыдущей статье - «Полный закон движения объектов в составе систем планетарного типа» [2] дано описание ранее не известных физических взаимодействий, которые формируют наблюдаемые орбиты движения планет и позволяют объяснить сложный характер движения Луны.

Согласно «Полному закону движения объектов в составе систем планетарного типа» [4], Луна относительно Земли (как и Земля, относительно Солнца), совершает движение в двух плоскостях – вращение вокруг Земли в плоскости экватора и, в виде периодических колебаний, в направлении движения планетарной системы Земля – Луна – см. фиг. 9.

В то же время, Луна вместе с Землёй совершает относительно Солнца, так же, движение в двух плоскостях – вращение в плоскости небесного экватора и, в виде периодических колебаний, в направление движения солнечной системы – см. фиг. 9.

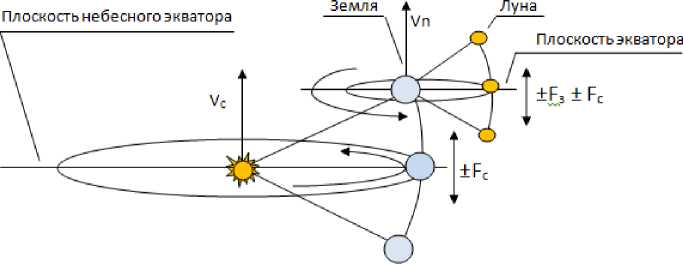
Фигура 9 . Физическая модель движения планет. Земля относительно Солнца и Луна относительно Земли условно показаны с одной стороны.

Сочетания этих движений и формирует наблюдаемую орбиту планет.

С уверенностью можно принять, что вращение планет в плоскости экватора является равномерным.

Как было показано в [2], основную роль в формировании наблюдаемой орбиты играют циклические колебания планет в направлении движения планетарной системы, происходящие под воздействием гравитационной составляющей F притяжения центрального тела.

Расчёт этого движения даёт представление о склонении в каждый момент времени, динамике изменения склонения и угле наклона плоскости вращения планеты. Так же даёт представление о продолжительности планетарных циклов и скорости движении планеты в направлении движения планетарной системы.

Суперпозиция циклических колебаний планеты в направлении движения планетарной системы и равномерного движения планеты в плоскости экватора позволяют построить наблюдаемую орбиту планеты, определить орбитальную скорость движения планеты по наблюдаемой орбите в каждый момент времени, и динамику изменения скорости её движения.

Расчёт колебательного движения Луны в направлении движения планетарной системы, необходимо выполнять, учитывая, одновременно, колебательные движения Земли относительно Солнца, колебательные движения Луны относительно Солнца и колебательные движения Луны относительно Земли.

Расчёт колебательного движения Луны в направлении движения планетарной системы и формируемого этим движением склонения Луны, выполняется по той же методике, что и расчёт склонения Земли (см. [4])

Итоговое ускорение Луны (для системы Солнце, Земля и Луна) складывается из ускорения, возникающего под воздействием гравитационной составляющей F _З притяжения Земли, и гравитационной составляющей F С притяжения Солнца, действующих в направлении движения планетарной системы – см. фиг. 10.

При этом векторы действия этих сил периодически как совпадают, так и направлены в противоположные стороны. В определённые моменты одна или обе указанные силы могут быть равны нулю.

Сложное сочетание действия этих сил, постоянно изменяющихся как по величине, так и по направлению, определяет сложный характер движения Луны.

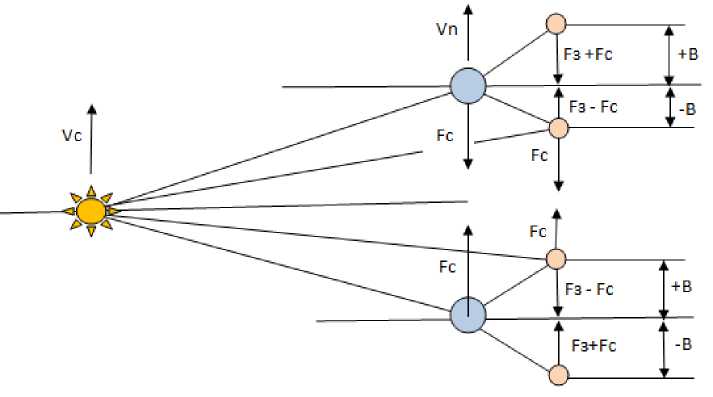
Фигура 10. Сложное сочетание действия гравитационных составляющих на Луну.

В таблице представлен фрагмент расчёта склонения (движения), Луны, происходящего под воздействием 114

Доклады независимых авторов 2016 выпуск 38 гравитационных составляющих F С и F З притяжения Солнца и Земли.

Расчёт выполнен с дискретностью 3600 сек. В интервале этого времени физические параметры, формирующие движение Луны, приняты не изменяющимися .

(Все представленные расчёты не являются окончательными, являются оценочными и требуют уточнения с учётом изменения расстояния планет от центрального тела, уточнения гравитационного взаимодействия при пересечении планетами экваториальных плоскостей, учётом ускорения Земли под воздействием гравитационной составляющей притяжения Луны, учётом гравитационного взаимодействия с другими планетами и ряда других возмущений…).

Таблица. Фрагмент расчёта склонения (движения), Луны, происходящего под воздействием гравитационных составляющих F _С и F _З притяжения Солнца и Земли. Для данного расчёта ускорение Луны, под воздействием гравитационной составляющей F С Солнца, принято равным ускорению Земли. Ускорения ΔV _З берутся из таблицы расчёта циклических колебаний Земли, выполняемого параллельно.

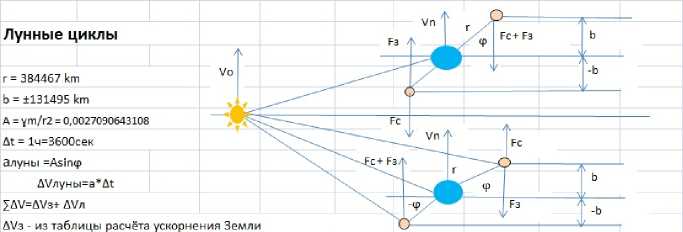
\/п=\/(п-1)-Д\/луны bn=b(n-l)-ASn

Элуны ДУлуны ^ДУ Vn S луны ASn км bn 5тф Склонение, 6 Источник* 219,736                       -82012,376 -0,2133145      12,3166 12,3166

• - 0,00057788 -0,0020804 -0,0105 219,7255 791011,699 957,8894 -81054,487   -0,210823 12,17058656

• - 0,00057113 -0,0020561 -0,0105  219,715 790973,885 965,2912 -80089,196  -0,2083123 12,02346557

• - 0,00056433 -0,0020316 -0,0105 219,7045   790936,16  972,605 -79116,591  -0,2057825 11,87531122

• - 0,00055748 -0,0020069 -0,0105  219,694 790898,523 979,8299 -78136,761   -0,203234 11,72613773

• - 0,00055057 -0,0019821 -0,0104 219,6836 790860,976 986,9653 -77149,795  -0,2006669 11,57595936

• - 0,00054362  -0,001957 -0,0104 219,6732 790823,519 994,0106 -76155,785  -0,1980815 11,42479041

• - 0,00053662 -0,0019318 -0,0104 219,6628 790786,153 1000,965 -75154,819  -0,1954779 11,27264522

• •    См. [3]

На графике 1 представлены результаты расчёта склонения (движения) Луны, формируемого циклическими колебаниями Луны в направлении движения планетарной системы, происходящими (колебаниями) под воздействием только гравитационных составляющих FС и FЗ притяжения Солнца и Земли – ряд 1.

На этот график наложены данные склонения (движения) Луны из публикуемых источников [3] - ряд 2 .

График 1. Циклы Луны под воздействием гравитационных составляющих   FС и FЗ притяжения Солнца и Земли, действующих в направлении движения планетарной системы.

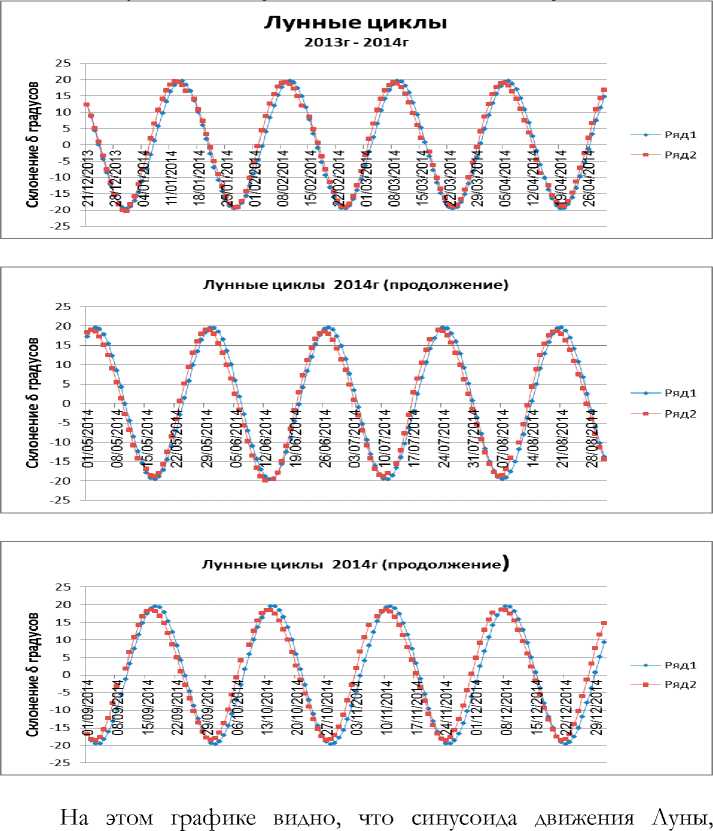
построенная на основании «Теории движения Луны» повторяет синусоиду, построенную на основании данных из публикуемых источников.

Результаты расчётов демонстрируют и подтверждают, что движение Луны и наблюдаемую орбиту формируют циклические колебания Луны, происходящие в направлении движения планетарной системы под воздействием гравитационных составляющих притяжения Солнца и Земли.

Во вступлении было отмечено, что в современных расчётах движения Луны используются десятки тысяч членов (коэффициентов и аргументов при тригонометрических функциях). Представленный расчёт выполнен с использованием, фактически, двух переменных – гравитационных составляющих F С и F З притяжений Солнца и Земли, действующих на Луну в направлении движения планетарной системы.

Полученные расчётом склонение Луны, динамика его изменения и продолжительность лунных циклов, формируемые колебательным движением Луны в направлении движения планетарной системы, согласуются с наблюдаемыми значениями и данными из публикуемых источников.

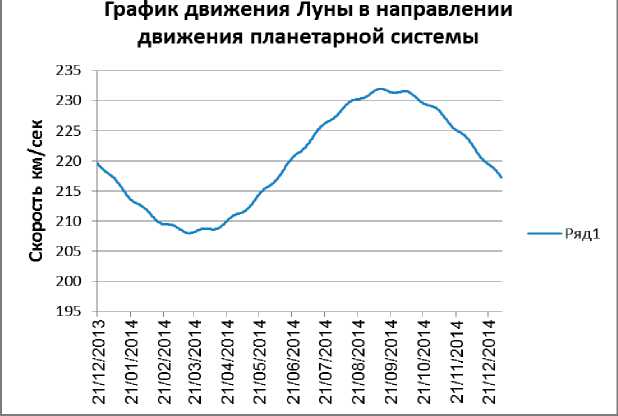
На графике 2 представлена диаграмма изменения скорости V _n движения Луны в направлении движения солнечной системы.

График 2. График отображает неравномерный характер движения

Луны в направлении движения планетарной системы. Это движение формирует неравномерное движение Луны по наблюдаемой орбите.

Вывод

Результаты расчёта циклов Луны подтверждают представленную «Теорию движения Луны» и верифицируют «Полный закон движения объектов в составе систем планетарного типа» [4].

Теория движения Луны и используемая методика расчёта позволяют учитывать влияние любого количества объектов на характер её движения.