Теория катастроф и каустики радиально-симметричных пучков

В классической геометрической оптике предполагается, что свет распространяется вдоль световых лучей. В однородной среде лучи представляют собой прямые линии. Одно из удивительных явлений в геометрической оптике – это образование каустик. Каустика представляет собой огибающую оптических лучей. Самые известные в природе каустики – обычная радуга и яркая линия, которая возникает после отражения света в обычной чашке с чаем. Мелкодисперсная среда рассеивает излучение во все стороны и визуализирует каустику. Каустики можно наблюдать в ясный солнечный день на дне прозрачного водоёма. Они образуются после преломления на криволинейной поверхности воды, созданной мелкими волнами. Геометрическую оптику [1, 2] можно рассматривать как коротковолновый предел классической оптики, которая, в свою очередь, основана на асимптотической аппроксимации системы уравнений Максвелла [2]. В основе коротковолновых асимптотик лежит факт, что поле описывается интегралами. Для того, чтобы вычислить интенсивность светового луча, необходимо вычислить интеграл. В рамках геометрической оптики обычно предполагается, что на интенсивность в данной точке оказывает влияние только небольшая область. На этом предположении строится вся геометрическая оптика. Можно показать, что во многих случаях увеличение области интегрирования не приводит к значительному изменению интенсивности в точке наблюдения. Математическим выражением этого факта является метод стационарной фазы [2]. Однако не всегда дифракционный интеграл можно вычислить с помощью метода стационарной фазы. В некоторых случаях использование этого метода приводит к появлению неустранимых особенностей. В этом случае интенсивность электромагнитного поля в точке стремится к бесконечности. Именно этот факт имеет место в окрестности геометрооптических каустик. Изучению каустик посвящено много работ. Классификация всех возможных каустик в общем случае была проведена В.И. Арнольдом [3]. Приложение теории катастроф к исследованию каустик изложено в [4, 5]. В работе [6] использован подход, альтернативный методу, основанному на интегральных представлениях от быстроосциллирующих функций. В работе уравнение Гельмгольца сводится к решению цепочки дифференциальных уравнений. Метод аналогичен сведению уравнения Гельмгольца к решению уравнения эйконала и переноса. Этот подход имеет некоторые преимущества, но позволяет найти поле только в окрестности неособой каустики. Различные асимптотические методы исследования уравнений и анализ поля вблизи особых точек изложены в работах [7–10].

В настоящей работе изучаются каустики осесимметричных пучков. В ряде работ анализ каустик проводится в параксиальном приближении. Однако следует отметить, что некоторые каустики при рассмотрении в рамках параксиального приближения исчезают. Примером может служить каустика параболического фронта. При рассмотрении в параксиальном приближении параболический фронт имеет только одну особую точку-фокус. В непараксиальном приближении появляется каустика, которая известна как ласточкин хвост. В данной работе каустики вихревых пучков исследуются в непараксиальном приближении. В работах, посвящённых теории катастроф, обычно не приводятся системы координат, в которых функции эйконала имеют канонический вид (обычно приводится только канонический вид). Это приводит к тому, что трудно использовать результаты этих работ для получения конкретных дифракционных картин в окрестности каустик. В работе построена удобная система координат, которая

. R 2 n

U ⁽ r , ^ф , z ) =-я /

^Л 0 0

позволяет в дальнейшем построить в явном виде асимптотики быстроосциллирующих интегралов.

1. Основные положения

Рассмотрим интеграл Кирхгофа в цилиндрической системе координат:

A ( p,9 ) exp ( ik ( ^ ( p, 9 ) + S ( p, 9, r , ф, z.

S ² ( p,9, r ,ф, z )

p d p d 9 ,

где в качестве эйкональной функции дифракционного оптического элемента (ДОЭ) рассмотрим радиальносимметричную функцию:

Другое решение, описывающее каустику, лежащую на оптической оси, имеет вид:

V ( p,9 ) = Ф ( p ) .

Тогда функция, стоящая в интеграле Кирхгофа под знаком экспоненты

Ф ( p,9, r ,ф, z ) = Ф ( p ) + S ( p,9, r ,ф, z ) ,            (3)

где S ( p,9, r ,ф, z ) = p ² + z ² + r ² - 2 r p cos ( 9-ф ) .

В приближении геометрической оптики интеграл Кирхгофа (1) можно вычислить с помощью метода стационарной фазы. Рассмотрим множество точек, для которых неприменим метод стационарной фазы. Это множество точек описывается системой уравнений:

^Ф PP ^Ф P9

^Ф p9 ^Ф 99

, Ф p = о , Ф 9 = 0.                 (4)

К этим уравнениям нужно добавить уравнение для стационарной точки функции эйконала:

Ф p ( p ) + S p = 0, S 9 = 0.

Решение системы уравнений (4) и (5) приводит к параметрическому уравнению поверхности особых точек

r ( 5 ) = ± ( S 0 ( 5 ) Ф 5 ( 5 ) + 5 ) ,

Ф = П + ( 1 + 1)|,

Z 0 (5) = V ^S0, UMS + r (4 ) 2 .

Параметрическое уравнение (6) аналогично полученным в работах [1, 11].

Функция S 0 удовлетворяет квадратному уравнению

a ( 5 ) S 0 ² ( 5 ) + b ( 5 ) S 0 ( 5 ) + c ( 5 ) = 0,                 (7)

где a (5) = 5^55 (5^5(5), b (5) = 53 {5Ф55 (5)+(1 -Ф52 (5)K (5)},          (8)

c ( 5 ) = 5 4 ( 1 -Ф 5 ( 5 ) ) .

Решение (7) имеет два корня. Один корень, соответствующий внеосевой каустике, имеет вид

^S 0 ( 5 ) =

Ф 5 ( 5 ) - 1 Ф 55 ( 5 )

S0 ^^W

Параметрическое уравнение каустики в декартовой системе координат имеет вид:

x = X0 (5, n) = r (5) cos ф(5,п), y = ^0 (5,n) = r (5)sinф(5,п),                    (11)

z = Z 0 ( 5 ) .

2. Криволинейная система координат

Метод стационарной фазы не применим для вычисления интеграла Кирхгофа в области каустики. Однако для вычисления поля в этой области можно использовать другие асимптотические методы, которые основаны на разложении функции под экспонентой в ряд Тейлора с точностью до членов выше второго порядка. Для вычисления интеграла Кирхгофа (1) в окрестности каустической поверхности введём криволинейную систему координат ( 5 , n , ^ )- Декарто-вые координаты связаны с введёнными криволинейными следующим образом:

x = X0 (5,n) + Nx (5,n)c, y = ^0 (5,n) + Ny (5,n)c,                        (12)

z = Z 0 ( 5 ) + N z ( 5,n ) c .

Величины N_x ( 5 , n ), N y ( 5 , n ), N z ( 5 , n ) представляют собой декартовые компоненты единичного вектора нормали, a - расстояние от каустической поверхности по нормали, при a = 0 точка лежит на каустической поверхности.

Для дальнейшего анализа рассмотрим квадрат расстояния между точкой на оптическом элементе с координатами ( p , 9 ) и точкой вблизи каустики с координатами ( 5 , n , a ),

S i ² = ( x - u ) ² + ( y - v ) 2 + z ². (13)

После подстановки выражений для криволинейных координат в окрестности каустики и на оптическом элементе получается выражение

S 1 ² ( p,9,5,n,a ) =

= S ² ( p,9,5,n ) + a ² + 2 f ( p,9,5,n ) a ,

где

s ² ( p,e,5,n ) = r ² ( 5 ) +p ² -

- 2 r ( ^ ) p cos ( n + ( 1 + 1 )( n /2 ) -e ) + Z 2 ( 5 ) , f ( p,e,5,n ) =

= r ( 5 ) a ( ^ ) + 2 Z 0 ( 5 ) b ( 5 ) -

- a ( 5 ) p cos ( n + ( 1 + 1 ) ( п / 2) -e ) .

где p выражено через x 1 , а e - через у 1 , J ( у 1 ) - якобиан преобразования:

^J ( у 1 ) =

4 R

V ( ² - ² у 2 )

Вычисление функций a ( 5 ) и b ( 5 ) приведено в Приложении.

Заметим, что интеграл (22) интересен в области малых значений y 1 , поэтому особенности в (23) не будет. А особенность при y 1 = 1 является устранимой.

Далее рассмотрим подэкспоненциальную функцию (17). С учётом (19) нам понадобится:

3. Вычисление в рамках теории катастроф

3.1. Внеосевая каустика

Теперь перейдём к постановке, характерной для теории катастроф. Рассмотрим функцию, которая в интеграле Кирхгофа находится под знаком экспоненты (подэкспоненциальная функция):

s ( p,e,5,n ) = V S 0 ² ( 5 ) + А ,                        (24)

где

А = R ( 2 5 + 2 r ( 5 ) ) x +

+ R ² x 2 ± 2 r ( 5 ) 5 у 2 ± 2 Rr ( 5 ) x 1 у 2 ,

F ( р,е,^,п,о ) = Ф ( р ) + S i ( p,e,^,n,o ) .         (17)

Для вычисления интеграла Кирхгофа (1) вблизи каустики в точке (5, n, °) учтём, что луч, приходящий

в рассматриваемую точку, исходит из точки

( p = 5 , е = n + (1 + 1) п /2) на апертуре. Далее вводим

следующие координаты:

x = p-5 ,

у = e-n + (1 + 1)п/ 2.

Диапазон изменения значений: x е [- 5 , R - 5 ], у е [- n + (1 + 1) п /2, 2 п - n +(1 + 1) п /2]. Учитывая радиальную симметрию, можно всегда положить n = 0. После некоторых преобразований можно записать расстояние от точки ( p , e ) на апертуре до точки вблизи каустики следующим образом:

s 1 ² ( p, e, 5, n, о ) = s ² ( p, e, 5, n ) + 2 f ( p, e, 5, n ) о , (19)

а расстояние от точки ( p , e ) на апертуре до точки непосредственно на каустике (при о = 0) будет:

S ² ( p,e,5,n ) = S 0 ( ^ ) + 2 ( 5 + r ( 5 ) ) x + + x ² ± 2 r ( 5 ) xC ( у ) ± 2 r ( 5 ) 5 C ( у ) ,

где C ( y ) = 1 –cos( y ).

Отметим, что C ( у ) е [0,2], т.е. принимает положительные значения, поэтому можем ввести новую переменную у 1 = ^C ( у ) / 2 . Для дальнейших рассуждений понадобится выражение старых координат через новые:

x = Rx1, у = arccos (1 - 2 у2),

где у 1 е [0,1].

Учтём описанные выше преобразования координат в интеграле Кирхгофа:

.      1 -5 / R 1

U ⁽^П, ^{о )} = ^-^ J J

^Л -5 / R 0

A ( p ) J ( у 1 ) s ² ( p,e,5,n,° )

X

^S 0 ( 5 ) =

ф5 -1 ф55(5)

Функцию Ф( p ), входящую в (17), разложим в ряд

Тейлора

да ф ( p ) = Z n = 0

1 dn Ф(^) n! d^ n

R n x ₁ n .

Функцию S ( p , e , ^ , n ) в (24) также разложим в ряд по степеням А .

Запишем выражение для подэкспоненциальной функции в виде:

F ( p,e,^,n,о ) = ф ( ^ ) + S 0 ( ^ )± ^ r ( l )^ у 1 ² + ^{s 0} ( 5 )

+ R ³

1d³ Ф ( ^ ) ф ^ ( 5 ) 1 Ф 1 ( 5 ) 3 ! d 5 ³ 2 S 0 ² ( 5 ) 8 S 0 ² ( 5 )

+2 R f + ^Ф' ' ) ± ^М( s „■ ( 5 )        s 0 ( 5 ) 1

₊ f ( p,e,5,n )

^{+   s} 0 ( 5 )    °

да

+Z

n = 4

1 - 2 ■ 3 ■ 5 a ⁴

+--- , / X +

2■4■6 ■ 8 sJ(5)

x 1 у ? +

1 d ⁿ Ф ( 5 ) n ! d 5 ⁿ

x 1 ³ +

Rⁿx n +

где f (p,e,5,n) =

= [ r ( 5 ) a ( 5 ) + 2 Z 0 ( 5 ) b ( 5 ) + a ( 5 ) 5] +            (27)

+ Ra ( 5 ) x 1 ± 2 a ( 5 ) 5 у 2 ± 2 Ra ( 5 ) x 1 у 2 .

X exp ( ikF ( p, e, 5, n, ° ) ) p d x 1 d у ,

Заметим, что выражение (26) в точке (0,0) будет иметь первую производную, равную нулю. Также гессиан в центральной точке (0,0) равен нулю. Это означает, что центральная точка является стационарной неморсовской точкой. Теория катастроф занимается анализом поведения функций именно в таких точках. При этом функции в этих точках с точностью до замены координат приводятся к некоторому набо-

ру канонических форм. Каждая из этих форм соответствует своему типу «катастрофы» [3 – 5].

Приведём (26) к каноническому виду. Тогда

где T n +1 – тейл («хвост») степени n + 1 и выше. Членами t n ₀ x n + T n _{+ i} пренебрегаем, и в результате получаем

функция F ( р , 9 , £ , п , ^ ) будет имеет вид

F ( р,9,^,п,с ) = F 0 ( ^,g ) + X 2 ( ^ ) y 2 + + t 30 ( ^ ) X 3 + t i2 ( ^ ) X i У 2 + P ,

где возмущение

P = Р 1 ( ^,c ) X i + p 02 ( ^,c ) y 2 + P 12 ( ^,c ) xy (.     (29)

Следует отметить, что на поверхности каустики функция возмущения (29) равна нулю.

Выражение (28) можно также представить в виде:

F ( р,еЛ,п,о ) = F ( ^,o ) + P i ( ^,o ) X + +^ 2 ( ^, о ) У 1 ² + 1 30 ( ^, o ) X 3 + t i2 ( ^, o ) X i y 2 .

В случае, если коэффициент при y ₁² не является малым, тогда с помощью осесохраняющего преобразования:

X i = X 2 ,

У 1 = У 2 + ( B 20 X 22 + B ii X 2 У 2 + B 02 У 22 )

уберём все члены третьего порядка, кроме x ₂³ :

F ( р,0Лп,о ) = ( p i X n + 1 30 x n } + X 2 y 2 +         (38)

Вернёмся к виду, полученному в (30), и подставим в интеграл Кирхгофа (22), выполнив замены переменных и расширив пределы интегрирования с учётом асимптотического характера интеграла:

U (^ n,o ) = - ( iz / X ) x

да да

x((

-да

A ( р ) J ( y i ( x 2 , y 2 ) )( i + ( B ii X 2 + 2 B 02 y 2 ) )

-да

S 2 ² ( x 2 , y 2 ,^,n,o )

x

x exp ( ik ( p _i x ₂ + 1 ₃₀ x 2 + X ₂ y 2 ) ) р d x ₂ d y ₂.

F ( р,9Лп,о ) = P i X 2 + X 2 y 22 + 1 30 x 2 ³ +

+ 1 40 X 24 + 1 3i X 23 У 2 + 1 22 X 22 У 22 + t i3 X 2 У 3 + 1 04 У 2 .

Якобиан преобразования (31) имеет вид:

d x _] d y_i d X ₂ d X ₂ d X ] d y_i d у 2 d у 2

i   ( 2 B 20 x 2 + B n x 2 y 2 )

^{0 i} + B ii ^X 2 + ² B 02 У 2

= ^{i +} ( B ii ^X 2 ^{+ 2 B} 02 ^y 2 ) .

Таким образом, в (32) остаются члены четвёртого порядка и выше. На этом можно остановиться, так как членами четвёртого порядка и выше можно пренебречь. В этом случае

F ( р, 9, £, n, o ) * p i x 2 + X 2 y 2 + 1 30 x 2 ³.

Если же продолжить процесс, то с помощью осесохраняющего преобразования:

У 2 = У 3 + ( B 30 X 3 ³ + B 2i X 3 ² У 3 + B i2 X 3 У 3 ² + B 03 У 3 ) ,

X 2 = X 3 ,

выбирая коэффициенты соответствующим образом, можно привести функцию (32) к виду:

F ( р,9Лг|,о ) = P i x 3 + X 2 y 3 ² + 1 30 x 3 ³ + 1 40 x 3 ⁴ + T 5 , (36) где функция T 5 содержит члены пятой степени и выше.

Дальнейшее продолжение аналогичного процесса приведёт к следующему результату:

F ( р,9Лп,о ) = p i X n +X 2 y 2 +

⁺ t 30 x n +... + t n 0 ^Xn ⁺ T n + i ,

В полученном выражении асимптотическая зависимость поля U ( ^ , n , о ) от о имеет вид функции Эйри [i].

3.2. Каустика вблизи оси

Рассмотрим оптический элемент, формирующий каустику вдоль оптической оси. В этом случае при вычислении интеграла Кирхгофа мы встречаемся с проблемой представления в канонической форме выражения, стоящего под знаком экспоненты

F(р,9,r,ф,z) = ф(р) + S(р,9,r,ф,z), где

S ( р,9, r ,Ф, z ) =

= ^р2 + z2 + r2 - 2rр cos (9 - ф)

Выражение для эйкональной функции для формирования осевой каустики имеет следующий вид [12]:

Ф ( р ) = -и=£^£_ , р ² + Z 0 ² ( р )

где Z ₀( р ) определяет распределение энергии вдоль каустики.

Будем искать поле в окрестности точки р = ^ , 9 = ф = n, z = Z о ( ^ ), для этого разложим функцию S ( р , 9 , r , ф , z ) в этой точке:

S ( р,9, r ,Ф, z ) =

р ² + z ² + r ² - 2 r р + 2 r р ( ] - cos ( 9-ф ) ) .

Перепишем в виде:

S ( р,9, r ,Ф, z ) =

= ( р- r ) 2 + z ² + 2 r р ( ] - cos ( 9-ф ) ) .

Обозначим у ² = (i - cos( 9 - ф )), тогда

S ( р,9, r ,ф, z ) =

= ^ ² + z ² + ( x ² + 2 ^ x ) + r ² + 2 r ( ^ y ² + xy ² - x - ^ )

или

где

S ( р,9, r ,ф, z ) = ^ ² + z ² +A ,                     (46)

А = 8о +81,

81 = r 8,

8 = - 2 к- r + x i -b y ² - x i y ² l 2

В окрестности каустики возмущение (52) имеет вид:

P 4 = P 1 ( b ) x 1 +^ 1 ( b ) x 2 +x 2 ( b ) y 2 + + 1 30 ( b ) x 3 + t 12 ( b ) x 1 y 2 + 1 22 ( b ) x 2 y 2 .

Разлагая S ( p , 9 , r , ф , z ) по степеням А в ряд Тейлора и эйкональную функцию в ряд Тейлора с точностью до членов второго порядка

Ф(p) = Ф(b)x -

( )      ( ) S0(b)

-

-

b2

А

21Sо (b) SО (b)

x2 +

получаем выражение для подэкспоненциальной функции в виде:

F (р,9, r ,ф, z ) = Ф(Ь) + S (b)--1кМ_ + ± 801 x4 +    84 + р (49)

8 S ³ ( b ) 16 S ⁵ ( b ) 8 S ³ ( b ) ^Щ S ⁷ ( b )     ’

где

_р _ 1 r 8 _ 1 r ² 8 ² + 2 r 8 0 8 +

= 2 S(b) 8    S3 (b)    +

1 r 3 8 3 + 3 r 88 0 + 3 r ² 8 о 8 ² _

⁺ 16          S ⁵ ( b )

- и 4

r ⁴ 8 ⁴ + 4 r 8 0 8 + 6 r ² 8 0 8 ² + 4 r ³ 8 ₀ 8 ³

S UJ

Далее удержим на поверхности каустики только члены, содержащие S ^–1, S ^–3 и линейные по r :

F (р,9, r ,ф, z ) = Ф(Ь) + S (b) +

+ 8 S3 (b/ x1

- 4 b x 3 >  jP 4 ,

где

р =f_81 808 '

4 lS(b) 2 S3 (b)?,

88 ₀ »- 4 c ² x 1 - 4 b x 2 - ( 2 x 1 ³ - 4 b ² x 1 y ² ) + 6 b x ² y 2 , (52)

8« 2 ( b + x i -b y 1 ² - x i y 1 ² ) .

На каустической поверхности возмущение в (51) будет равно нулю, т.е. rP 4 =0. В этом случае после подстановки выражения (51) в интеграл Кирхгофа мы получим выражение:

U ~ J A( x 1 ) exp <  ik

l x 4 - 4 b x 1 ³ ) 8 S ³ ( b )

• d x 1 .

После замены переменных x 1 = x ₂ + b интеграл сводится к интегралу:

f x 4 + ^ x 2 + t\xi 1

U ~ (A( x ₂ )exp j ik    —² 2 / ^{2 J} ^ d x ₂,

J 2           [ ^      8 S3 (b)      J 2,

который асимптотически сводится к интегралу Пирси [1].

Если бы коэффициент при y 1 имел большое значение, то переменная y ₁² была бы «хорошей» [5] и тогда с помощью осесохраняющего преобразования только «хороших» переменных можно было убрать перекрестные члены, содержащие «плохие» и «хорошие» переменные выше третьей степени, и функцию привести к виду

F (p,9, r ,ф, z ) = Ф(Ь) + S (b) +

⁺ 8 S 3 1 ( b )¹ x 2 ^{4 - 4 b} x 2 ^{3 1 + X} 2 ^{( b )} y 2 ².

Однако это не так. Это означает, что в этом случае невозможно представить выражение в виде канонического ростка и его возмущения. Это связано с тем, что в отсутствие возмущения все количество стационарных точек стремится к бесконечности.

Теорию катастроф целесообразно применять для анализа, когда имеется конечное число стационарных точек, которые сливаются. Возмущение приводит к тому, что вместо одной вырожденной неморсовской точки появляются несколько псевдоморсовских точек (происходит «морсификация»). В нашем случае ситуация иная и применять подход, основанный на анализе форм Тома, нецелесообразно. Подобный случай наблюдается вблизи фокальной точки, где росток катастрофы представляет собой константу и стационарные точки занимают всю плоскость.

4. Альтернативный подход

В предыдущих параграфах мы пытались свести подэкспоненциальную функцию к формам Тома. Этот процесс нелёгкий и приводит к громоздким выражениям. Для того, чтобы вычислить интеграл Кирхгофа вблизи оси, воспользуемся следующим представлением подэкспоненциальной функции:

F (p, 9, r ,ф, z ) = ф(р) + S (p, r, z )x

-

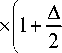
А ² А ³ --1---+ 816

1-2-3-5 1

^{1 2 3 5} А⁴ I ,

2-4-6-S у

где

S (p, r, z) = V (p- r )2 + z2,2 r p(1 - cos (9-ф))S2 (p, r, z)

Вблизи оптической оси используем только первый член разложения:

F (p,9, r ,ф, z ) = ф(p) +

Sorb)cos (9"ф) •

тогда интеграл Кирхгофа:

rpS (p, r, z)

+ S (p, r, z)-

U ( r ,ф, z ) = ikz J A ( p ) x 2 n

( (           r p exp ik Ф^p)^—?-----г

^PI ( ^(P) S ( p, r , z )

X

x exp

— ik

S ² ( p, r , z )

) '   cos ( 9 —ф ) p d p d 9 .

S ( p, r , z )              J

X

Интегрируем по углу

R

U ( r ,ф, z ) = ikz Jo ( ( ..

x exp ik Ф ( p ) +

A ^{( p )} _X

S ² ( p, r , z )

та⁺ S ⁽ p, r --*

X

X J 0

(    1

kr p

₄ S ( p, r , z ) _?

Р d p .

Заметим, что интеграл (61) отличается от непараксиальной аппроксимации интеграла Кирхгофа, рассмотренной в работах [13, 14].

Полученный асимптотический интеграл удобен для расчётов и в параксиальном приближении сводится к преобразованию Френеля – Ханкеля.

5. Результаты моделирования

В данном параграфе выполнено численное сравнение расчета поля для параболической и сферической линз в непараксиальном режиме с использованием трех типов операторов распространения: разложение по коническим волнам [15, 16], преобразование Френеля – Ханкеля и выражение (61).

На рис. 1 показаны результаты расчета для сферической линзы:

Ф ( p ) = — Vp ² + f ² .                           (62)

На рис. 2 показаны результаты расчета для параболической линзы:

Ф ( p ) = —p ²/2 f .                                (63)

Параметры расчета: радиус оптического элемента R = 126 X , фокусное расстояние f =50 X .

Как видно из результатов моделирования, представленных на рис. 1 и 2, полученный в работе асимптотический интеграл (61) позволяет получать корректные расчеты, очень близкие к результатам точного моделирования на основе разложения по коническим волнам.

Интересно также отметить различие, которое имеет место для сферической и параболической линз в непараксиальном случае.

Заключение

В работе рассмотрено вычисление поля вблизи каустики, формируемой с помощью радиально-симметричного ДОЭ.

в)

Рис. 1. Результаты расчёта (негатив) для сферической линзы (62) с использованием разложения по коническим волнам (а), асимптотического интеграла (б) и преобразования Френеля – Ханкеля (в): ход лучей (верхняя строка, z e [25 X ; 75 X ], y e [-5 X ; 5 X ]) и распределение

интенсивности в фокальной плоскости

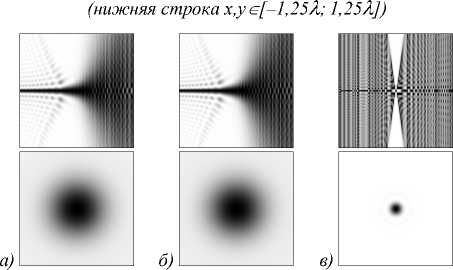
Рис. 2. Результаты расчёта (негатив) для параболической линзы (63) с использованием разложения по коническим волнам (а), асимптотического интеграла (б) и преобразования Френеля – Ханкеля (в): ход лучей (верхняя строка, z e [25 X ; 75 X ], y e [-5 X ; 5 X ]) и распределение интенсивности в фокальной плоскости (нижняя строка x,y e [-1,25 X ; 1,25 X ])

Получено представление интеграла Кирхгофа с использованием канонических форм, которые обычно применяются в теории катастроф. В отличие от других работ, интеграл Кирхгофа рассмотрен в цилиндрической системе координат. Результат представлен в криволинейной системе координат, согласованной с каустической поверхностью.

Полученное асимптотическое представление интеграла Кирхгофа вблизи оптической оси отличается от непараксиальной аппроксимации интеграла Кирхгофа, рассмотренной в других работах. Результаты моделирования на примере сферической и параболической линз показали корректность расчетов с использованием асимптотическго интеграла в непараксиальном случае.

Результаты, полученные в данной работе, можно обобщить для вихревых пучков.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант № 18-29-20045-мк) в части численного моделирования и Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фото-

ника» РАН (соглашение № 007-ГЗ/Ч3363/26) в части теоретических выкладок.