Теория когерентных фокусаторов

В последнее время для решения ряда технических и научных задач стали использоваться оптические приборы нового типа - фокусаторы, назначение которых - фокусировка излучения не в точку, а в линию. Теория фоку-саторов [1-4] ставит своей целью определить поверхности линз, зеркал, зонных пластинок и т.д., преобразующих заданное первичное поле Uo в поле U, фокусирующееся в требуемую фокальную линию F(o), вдоль которой задано распределение интенсивности поля I (о) . Естественно, что в силу эффектов дифракции ширина зоны фокусировки (диаметр трубки, ось которой - фокальная линия) конечна и определяется отношением поперечного размера фокусатора к длине волны.

Интенсивность поля на фокальной линии можно понимать двояко: или как интегральную величину - поток энергии на единицу ее длины по поперечному сечению зоны фокусировки (ширине фокального пятна), или как локальную величину - квадрат амплитуды поля на самой фокальной линии. Неоднозначность определения интенсивности, различие в конструктивных особенностях фокусаторов, а также ряд дополнительных обстоятельств приводят к различным вариантам формулировки теории фокусаторов.

В любом случае, если не учитывать дифракционные эффекты, связанные с концами фокальной линии, задача определения поверхности фокусатора, то есть функции двух переменных, может быть сведена к определению функции одной переменной - закона изменения эйконала s(о) вдоль самой фокальной линии (о - длина вдоль фокальной линии). Функции s(о) и Е(о) определяют лучевую структуру поля фокусировки.

Ниже на нескольких примерах показано, что во всех вариантах теории задача сводится к решению обыкновенного дифференциального уравнения относительно s(о). Различие в определении интенсивности и конструкции фокусатора приводит к отличию дифференциальных уравнений относительно S (о) .

Лучевая структура поля, Фокусируемого в фокальную линию

Через каждую точку фокальной линии проходит круговой конус лучей (рис. 1)*. Одна половина конуса соответствует лучам, приходящим к фокальной линии, другая - уходящим от нее. Ось конуса касательна к фокальной линии, угол раствора ш(о) определяется производной ds/do [5]: , . ds cosw(o) =                                                               (1)

Для последующих расчетов удобно использовать систему координат о, ф, р, связанную с лучевой структурой, в которой ф - угол, характеризующий луч в конусе о (далее ф - угол, отсчитываемый от соприкасающейся (с фокальной линией) плоскости А, р - расстояние вдоль луча от вершины конуса до рассматриваемой точки М(р>0 на конусе приходящих лучей и р<0 на конусе лучей, уходящих от фокальной линии).

Система координат о, ф, р не является лучевой, так как поверхности p=const отличны (см. формулу (5)) от поверхностей s=const.

Рис. 1

Координаты о, ф, р однозначно определяют положение точки М. Обратное утверждение в общем случае несправедливо. В многолучевых областях пространства, где через точку М проходит п лучей, каждой точке соответствует п наборов координат о, ф, р. В областях, где лучей нет, координаты о, ф, р комплексны.

Вектор М(о, ф, р) связан с вектором F(a) точки на фокальной линии и ортом q0(o, ф) луча в конусе соотношением:

М(о, ф, р) = F (о)+q (о, Ф)«р.                                        (-)

О

В соответствии с приведенными определениями о и ф q0(a, Ф) =т (a) «Созы (о) +n (a) -sinw (а) -созф+b (о) .sinco (о) • з!пф, (3) где т, n, b - орты касательной, нормали и бинормали к F(о).

Поскольку и ориентация оси конусов, и их угол раствора являются функциями о, семейство конусов по параметру о имеет огибающую - каустическую поверхность рассматриваемого лучевого поля*. Уравнение этой ПО-

Ф)

S'' (О)СО5ф       ~1                                      (4 j з1п2ш(о) е (о)‘sina)(a)

где

- расстояние от точки F(о) фокальной линии вдоль луча с, ф до каустической поверхности;

е(о) - радиус кривизны фокальной линии.

Значение эйконала S лучевого поля в точке о, ф, р: S (о, ф, р) = s (о) - р(о,ф).

Связь поля на поверхности фокусатора и интенсивности I(о)

На поверхности фокусатора S первичное поле U_Q преобразуется в поле U(о, ф, р) , фокусирующееся на линии F (о) . Будем считать известными поверхность фокусатора Е и распределение поля U на ней, а также F(o) и значение на ней эйконала s(о). В окрестности Е справедлива геометрическая оптика. Поэтому поле U на Е можно записать в геометрооптической форме*:

U = Ajo*, ф*)е1к si(o*' Ф*> •

Контур Г поверхности фокусатора будем считать заданным в форме (рис. 2):

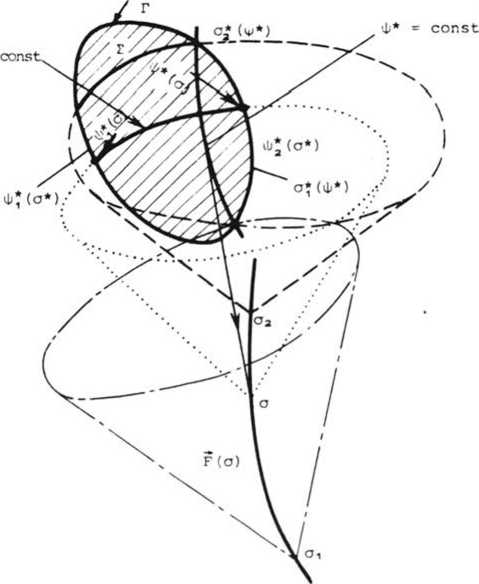
Рис. 2

то

о*(ф*) < а* <а*(ф*); (ф*. <ф*<ф*  ), а также ф*(о*) < ф < ф*(а*) 7 (omin-°*-amax)'

В окрестности фокальной линии, где геометрическая оптика неприменима, поле U(о, ф, р) будем определять, используя формулу Грина-Кирхгофа по полю U(о*, ф*) на Е. Будем считать, что функция s(о) такова, что через каждую точку Е проходит только один луч, то есть каустическая поверхность х(о, ф) не пересекает Е, что возможно, если х<0 (каустическая поверхность мнимая) или x>r (Е расположена до каустической поверхности).

Поле U(о), записанное с помощью формулы Грина-Кирхгофа в переменных интегрирования о*, ф* для точки наблюдения Г(о), расположенной на фокальной линии, имеет вид:

Ф*тах     о*(ф*)

U(o) = ^ / аФ* / А (о*, ф*) . cosa-Colt^-t-COs^to^o^k^Lx И Ф*^      о*(ф*) 12

min1 еik[S1(о*,ф*) + а(о,о*,ф*)]

х---- а(о*,ф*)ао*,(6)

d(а,о*,ф*)

где а - угол между лучом и нормалью к Е в точке о*, ф*;

Р - угол между той же нормалью к Е и вектором, соединяющим точку наблюдения Г (о) и точку интегрирования г(о*, ф*);

d - расстояние между точкой интегрирования и точкой наблюдения;

J - якобиан в координатах о*, ф* .

Используем для вычисления интеграла по о* метод стационарной фазы. Точкой стационарной фазы, в силу принципа Ферма, является точка о*=о, из которой в Г(о) приходит луч геометрической оптики (см. рис. 2). Вычисляя при о*=о величины a, Р, а, J,входящие в (6), и пренебрегая вкладом краевых (контурных) слагаемых, то есть заменяя конечные пределы интеграла по о* бесконечными, получим [б1:

Ф* (о)                 ,-------------------------------- и(о) =         J д (о               ф*) - г(о,_ф*)_1 х

2п ф*(О)   1                  |Х(О, ф*)| xeitMS^a, Ф*) + a(a, о*, Ф*) ) - sgn(s"(а))] х /г(Ог ф*)аф*.

В силу (2) , (3)

и = х (ф*, о, s 1 (о) , s" (о) ) , г = г(ф*, a, s1(о)).

Поскольку в точку F(o) приходит конус лучей, соответствующих линии стационарной фазы о*=о, то в соответствии с (5)

S₁(о, ф*) + d(o, а, ф*) = s (о) и, следовательно, ф* (_О)

и(о) . /Ц e^kslo) + s9n(stoll] , , д |а,ф.)/45ТТ7 . аф-. (7) ф* (о)

Поэтому искомая связь между интенсивностью 11 (о), понимаемой как локальная величина, то есть квадрат амплитуды поля на самой фокальной линии, выражается через интеграл на Е по линии о*=о

Ф*а ---------- la

1,(0) = IUI- - к-.

или, в симводической форме,

I^o) = нДо, s'(o), s" (о) , ф*(о, s'(o)) , ф*(о, s 1 (о) ) J.          (8')

Вычислим далее интенсивность 1а(о), используя другое, интегральное ее определение [1], то есть полагая ее равной потоку энергии, проходящей через площадку шириной, равной диаметру фокального пятна, и высотой do. В силу закона сохранения энергии этот поток равен потоку энергии через ленту на Е, края которой - линии о и o+do. При таком определении Ф* (а)

I (о) = У А2 (о, ф*) • J(o, ф*) • cosa(o, ф*)dф* = 2 ф* (а)

ф*(а)

= sinco(о) • У А2 у ।1 г • бф*,(9)

Ф*(о)

то есть I3(o) = Н2[о, s*(o), s" (а) , ф* (о) , ф*(о)].О')

Уравнение для Sja*, ф*)

В предыдущем разделе рассматривались прямые задачи, то есть функция s(о) на фокальной линии считалась заданной. Поэтому была известна и координатная сетка о*, ф* на поверхности Е, а также функции S1(a*, ф*), А1(о*, ф*), задающие поле U1 = А^ 1, прошедшее фокусатор. Интенсивность же, то есть функции I (о) или I (о), являлась искомой.

1                 2

Ниже решается обратная задача: задается I(о), а определить необходимо функцию S1(о*, ф*). Как следует из вышеизложенного, для этого достаточно определить функцию s(о). Функцию А1 на Е будем считать известной. Такой постановке обратной задачи соответствует фокусатор в виде тонкой (в том числе и зонированной) линзы, которую можно трактовать как фазовый трансформатор, преобразующий падающее на Е первичное поле ik S                  ik S

Uo=Aoe ° в поле U1=Aoe 1 без изменения амплитуды. Изменение эйконала при прохождении фазового трансформатора

<р (о*, ф*) = S^a*, ф*) - SQ(o*, ф*) и определяет структуру фокусатора, то есть зависимость его оптической толщины от координат.

Решение поставленной задачи сводится к решению уравнений (81) или (9*) (в зависимости от используемого определения интенсивности I (о) ) относительно функции s(о). Эти уравнения являются обыкновенными дифференциальными уравнениями (не разрешенными относительно старшей производной, то есть s" (о)). Поскольку ив (8*) , ив (9*) входят лишь s' ив", а сама функция в не входит, то относительно функции n(o)=s’(o) (8') и (9*) являются уравнениями первого порядка вида:

с1 • 11 (о) = Н1 (о, и, П*) ;                                               (Ю)

с2 • 12(о) = Н2(о, и, И1),                                         (Ю1)

в которых интенсивности 11 или I заданы с точностью до нормирующих множителей ciZ с2. Эти множители, а также начальные значения rimin определяются из граничных условий: конуса лучей, исходящие из двух концов фо кальной линии,

то есть о . ио min max

должны касаться (не пересекая)

кон

тура Г поверхности фокусатора S (рис. 3).

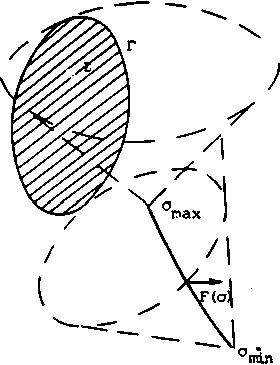
Рис. 3

Решение дифференциального уравнения (10 или 10') при указанных гра ничных условиях дает распределение эйконала s(о) вдоль фокальной линии*, что определяет лучевую структуру поля U. Это позволяет записать уравнение для поверхности 5 в форме г=г(о, ф) . Далее с помощью (5) рассчитывается 51(о*, ф*) , что достаточно для определения толщины тонкого зонированного фокусатора. Существенно, что физически реализуемы лишь те решения, в которых каждой точке Г соответствует лишь один луч. В случае, когда решение не обладает этим свойством, постановку задачи следует модифицировать - или изменить взаимное положение фокальной линии и фокусатора, или сделать на X дополнительный разрез, то есть модифицировать контур Г [7].

♦Решение в (о) должно быть однозначной функцией о, то есть через каждую точку о должен проходить лишь один конус лучей.

Решение уравнений (10) и (10') производится в общем случае численно. Для применения численных алгоритмов интегрирования дифференциальных уравнений необходимо на каждом шаге определять численное значение производной д', рассматривая (10) и (10*) как трансцендентные уравнения относительно нее.

Различие (10) и (10'), связанное с разной трактовкой интенсивности, приводит к различию решений для s'(о), а следовательно,к разным S^o*, ф*) . Иными словами, структуры фокусаторов при разном понимании интенсивности отличаются друг от друга. Проиллюстрируем различие решений на простейшем примере фокусатора, геометрия которого показана на рис. 4. Фокусатор - плоский, его контур Г - равнобедренная трапеция с основаниями 1; 0,1 и высотой 1. Фокальная линия - прямая, расположенная параллельно плоскости фокусатора симметрично относительно его боковых сторон. Расстояние f от фокальной линии до фокусатора 10 или 100. Ее длина 0,5 (о, = -0,25; о = 0,25). Распределение амплитуды по плоскости фокусатора А(у) = [ау + р]~а(а = 0,45; & = 0,275) соответствует (см. ниже) линейному закону отображения для интегрального определения интенсивности. Поскольку в примере f»l, то справедливо параксиальное приближение, то есть можно положить r=f; h=(s")~¹ и записать (9) в виде:

s" • f = ^ - 1.                                                       (11)

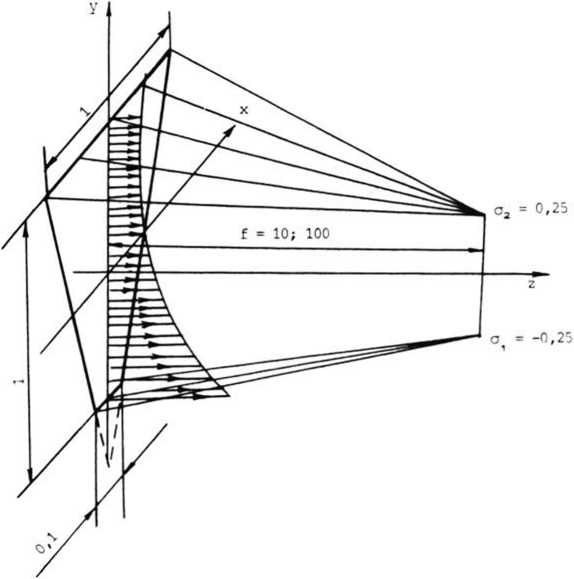
Рис. 4

Две константы, входящие в решение (11) (с и константа, возникающая .                                                          2                                  , при интегрировании), определяются из граничных условий: конуса, соответствующие концам фокальной линии, должны излучаться нижним и верхним основаниями трапеции.

Решение (11) является линейной функцией:

s' (о) = А2(о - oj + Вз,                                             (12)

где            р

₌    1         ^Уа~ °а _ У1 *        . _{в =} У_а "

°2~°1 / (У₃^_о₂)² + f²*  >/ (У,"®,) ² + f²_   ² V ^-а^² + f²'

Уравнение (8) , соответствующее другому - локальному-определению интенсивности 2 пс

(1 + f • s") • (о + f • s') = j^-,                                   (13)

дает решение s' = [А, • (O-Oj + Bj1/» - o/f,                                 (14)

отличное от (12).

Заметим, что в силу граничных условий решения (12) и (14) (рис. 5) совпадают в точках о = ±0,25, соответствующих концам фокальной линии. Наибольшее различие между (12) и (14) наблюдается в середине фокальной линии. Различие более существенно для короткофокусной системы (f = 10).

Отметим, что в параксиальном приближении функция s'(о) не зависит от формы поверхности Е, а зависит лишь от формы контура Г (точнее - его проекции на плоскость фронта первичной волны). Однако от формы поверхности зависит так же, как и от функции s'(о), фазовая структура фокуса-тора <р (о* , ф*) .

Синтез поверхности зеркального Фокусатора

В рассмотренной выше постановке задачи фокусатор предполагался тонким (например, зонированным), а его поверхность 5 - заданной. Это приводило к дифференциальным уравнениям для s(о), содержащим только производные s'(o) и s"(о). В случае, если глубина фокусатора велика, наряду с s' и s" в уравнение входит и сама функция s.

Покажем это на примере задачи синтеза зеркального фокусатора (рис. 6), в которой искомая функция R(o, ф) - поверхность зеркала, преобразующая первичную сферическую волну (центр волны - точка Q на рис. 6) в поле U, фокусирующееся в фокальную линию F (о) , вдоль которой задана интенсивность I(о). Первичное поле U - направленное. Оно отлично от О нуля в телесном угле, граница которого - конус 0 (эквивалент контура Г в предыдущей задаче), в котором оно характеризуется диаграммой Ф(0,ср) . Как и ранее, вначале решим прямую задачу, то есть интенсивность I(о) будем считать искомой, а функцию s(о) - заданной.

s 1 (о)

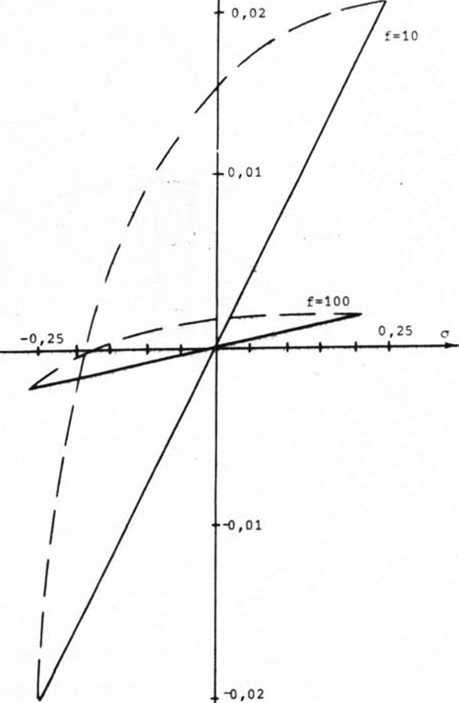
---- Для интегрального определения интенсивности

--- Для локального определения интенсивности

Рис. 5

Рассмотрим линию (полосу)X зеркала, преобразующую лучи первичной сферической волны в конус лучей, приходящих в точку на фокальной линии. Линия об образована пересечением этого конуса с эллипсоидом вращения Т(о) (рис. 6), фокусы которого расположены в точках Q и F(o). Длина оптического пути, то есть большая ось эллипсоида, равна сумме s(о) и произвольной константы h [8].

Положение одного фокуса, то есть F(o), и оптическая длина s(о)+h являются, таким образом, функциями о. Семейство (по параметру о) линий Хи образует поверхность зеркала.

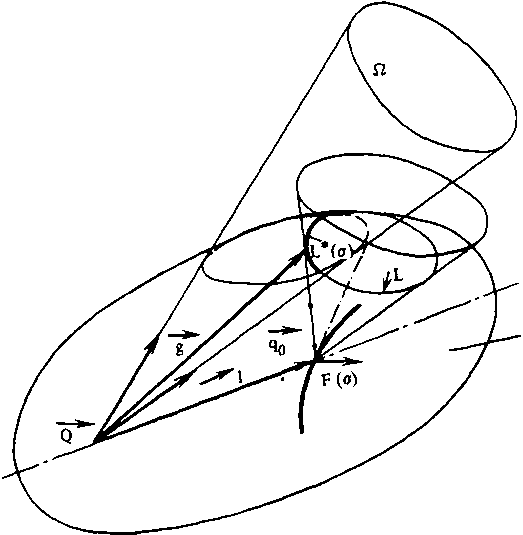
Т (о)

Рис. 6

Очевидно, что имеет смысл использовать для зеркала лишь участок ^ линии ^ , расположенный внутри конуса 0, где амплитуда первичного поля отлична от нуля.

Параметрическое представление поверхности зеркала в координатах о, ф имеет вид:

Н(о, ф, s(o), s'(о)) = ------------Е^2---------------,             (15)

1 - 6(a) • (То (о) . д0(о,ф))

где R(o, ф) - расстояние от точки Г (о) фокальной линии вдоль луча ф до зеркала;

р (о) = [ (s (о)+h) 2-1 (о) 2]/2 [s (о)+h] - фокальный параметр эллипсоида;

• 6 (а)* 11(о)I/[s(о)+h] - его эксцентриситет;

(Т(а)|=|Е(а) - QI - межфокусное расстояние эллипсоида;

Ч0(о, ф) - орт отраженного луча в конусе (3) ;

То(о) = ^(°)/11(о)1 - орт оси эллипсоида.

Проводя выкладки, аналогичные приведенным выше, запишем интенсивность I (о) на фокальной линии с помощью формулы Грина-Кирхгофа:

Ф* (а)

- 2п

ф* (а)

Ф[б(о,ф*),ф(а,ф*)] /

Is (Н)+Ь-К(о,ф*) | V К^»Ф )

к(а,ф*)

оф*

Угловые координаты 6, ср, в которых задана диаграмма, выражаются через координаты а, ф с помощью закона зеркального отражения (см. рис. 6): д(6, ср) = 1(a) - qo(a, ф) • R(a, ф) ,                                (17)

где д(6, ср) - вектор, проведенный из точки источника в точку зеркала. Таким образом, решение прямой задачи дается совокупностью формул (15), (16)*.

Перейдем к решению обратной задачи. Теперь 1(a) не искомая, а заданная функция. Используем для решения формулу (16), полагая в ней s(о) не известной, а искомой функцией. Ясно, что в этом случае (16) следует рассматривать как дифференциальное уравнение второго порядка относительно s(a), заданное в неявной форме:

с3 • Ко) = Нэ(о, s, s', s ") .                                         (18)

В отличие от (8'), (9'), оно содержит не только первую и вторую производные, но и само значение эйконала, то есть является дифференциальным уравнением второго порядка, не разрешенным относительно.старшей производной. Искомое решение s (а) должно удовлетворять граничным условиям - линии зеркала, соответствующие концам фокальной линии a=ai, o=a2, должны касаться граничного конуса Я первичного поля, не пересекая его. Это условие определяет значения s(a1), s'(ai) и s(o2), s'(a2). Константа сэ вычисляется через s(a2), s'(o2). При указанном выборе начальных условий для s(а) полученная поверхность фокусатора расположена внутри конуса Я, причем ее граничный контур Г лежит на самом конусе Я.

Для интегрального определения интенсивности задача синтеза зеркального фокусатора также сводится к дифференциальному уравнению второго порядка относительно s(a). Начальные условия и константа с3 определяются из условия равенства потоков энергии в конусе Я первичной волны и через фокальную линию.