Теория кругового термического ионизатора (1973, 1977 гг.)

Рассматривается теория кругового термического ионизатора. Несмотря на то что две работы с авторским участием Ю.К. Голикова, из которых скомпилирована данная статья, были впервые опубликованы достаточно давно, они по-прежнему сохраняют свое значение. В частности, следует отметить, что характеристики чувствительности термоионизационного источника ионов урана (ЖТФ. 1970. Т. 40, № 7. С. 1534–1536), который использует данную теорию, до сих пор остаются рекордными.

Кл. сл. : источник ионов, термоионизатор, эффективность ионизатора

ПРЕДИСЛОВИЕ

Две статьи, сведенные здесь воедино как разделы, были опубликованы в 1973 г. [1] и в 1977 г. [2]. Теория, которая рассматривается в этих работах, служит основой термоионизационного источника ионов урана, чьи характеристики по чувствительности и по настоящее время являются непревзойденными (см. [3]).

Основное достоинство термического ионизатора, рассмотренного в данных статьях, состоит в следующем. Ионизатор представляет собой трубку диаметром 3 и длиной 24 мм из вольфрамовой фольги толщиной 20 мкм, закрытую с одного торца заглушкой. Трубка нагревается до температур 2 500–2 700 °С постоянным током таким образом, что плюс напряжения накала приложен к заглушке. Это обеспечивает внутри трубки постоянное электрическое поле ~ 0.5 В/мм, направляющее ионы к открытому концу трубки. В трубку вблизи заглушки вставлен испаритель, на который наносится исследуемая проба урана. Нейтральные атомы урана, попадающие из испарителя в ионизатор, испытывают внутри трубки столкновения с ее поверхностью, приводящие к их ионизации в каждом столкновении с коэффициентом ~ 10–3. Однако из-за многократности столкновений со стенками общий коэффициент ионизации для урана приближается к величине 0.5, т. е. ионизуется каждый второй атом урана. Следует отметить удачное техническое решение по созданию вытягивающего электрического поля в [3]: оно создается "само собой" из-за градиента потенциала вдоль нагревателя, который обусловлен конечной проводимостью нагревательного элемента и свя- зан с протекающим по нагревательному элементу электрическим током. Полученный результат по эффективности ионизации и, следовательно, по чувствительности анализа загружаемой в ионизатор пробы является рекордным даже по меркам нашего сегодняшнего времени.

В статьях-разделах, следующих за этим предисловием, изложены теоретические подходы к анализу и оптимизации описанного выше устройства "Термический ионизатор, совмещающий в себе черты камеры Кнудсена с системой направленного вытягивания ионов, образовавшихся при термоионизации" [4]. Следует отметить, что определение равновесного самосогласованного распределения частиц в устройстве типа камеры Кнудсена представляет собой весьма нетривиальную математическую задачу и решается в указанных статьях с исключительной элегантностью, маскируемой внешней простотой и "очевидностью" выкладок. За исключением исправления немногочисленных опечаток, текст статей сохранен в неприкосновенности.

1. К ТЕОРИИ ТЕРМИЧЕСКОГО ИОНИЗАТОРА [1]

Под термическим анализатором мы понимаем металлическую поверхность (или систему металлических поверхностей), применяемую для эффективной ионизации потока нейтральных атомов [4]. Качество ионизатора определим отношением K = I_i I , где I_i — интенсивность выводимого наружу ионного потока, а I — интенсивность первичного нейтрального потока. Работает ионизатор следующим образом.

Первичные нейтральные атомы попадают на одну из горячих поверхностей и отражаются, частично ионизуясь с коэффициентом ионизации α . Отраженный поток вновь попадает уже на другие горячие поверхности, на которых нейтрали также ионизуются, а ионы рекомбинируют с тем же коэффициентом α , и т. д. В результате этих многократных отражений в системе, в конце концов, устанавливается равновесный поток нейтралей и ионов, проходящий сквозь ионизатор. Эффективность K ионизатора нарастает, если ионы удалять из системы вытягивающим электрическим полем раньше, чем они вновь попадут на горячую поверхность. Увеличивая вытягивающее поле, можно достичь режима полного отбора ионов. Соответствующая ему величина K характеризует степень оптимальности выбранной геометрии ионизатора.

Рассчитаем величину K при полном отборе для простейшей системы, состоящей из двух параллельных пластин A и B (рис. 1). Ионы вытягиваются полем вдоль оси x . Источник первичного потока интенсивности I представляет собой щель в точке O . Пусть угловая функция распределения первичных нейтралей есть p ( у ) , а вторичных нейтралей f ( у ) , где углы у и у отсчитываются от нормалей к стенкам (см. рис. 1). Условие нормировки p и f имеет вид

π2

J p(у)dy = J f (y)dY = 1,(1)

- П 2

где у = arctg x/h . y = arctg ( ^ - x )/ h .

Обозначим плотность выделения вторичных нейтралей с пластины A как n ( x ) , а с пластины B как n 2 ( x ) . Простое рассмотрение баланса частиц приводит к системе интегральных уравнений

П , ⁽ x Н^{1 - а} ) IP^у ) d x ■ Jn ( ^ ) f ⁽ Y ) d | d ^ ,

-а

П 2 ^{( x} М^{1 - а} ) J n , ' - ) f ⁽ Y ) d Y ^d ^ .

Сложив уравнения (2), получим одно уравнение относительно суммарной плотности Ц = П 1 + n 2 :

+

ц ( x ) = Q ( x ) + J F ( ^ - x ) ц ( ^ ) d ^ ,      (3)

-a где

Q = (1 - a) p (y) -TIhr? x +h а ψ и γ берутся из (1).

F = ( 1 - a )

h ²

( ^ - x ) 2 + h²

Решение (3) ищем в виде ряда Фурье to П i nx ц = ^ cnea , разложив при этом обе функции

-to

ππ i nx                          i nx

Q = \ gne a и F = / ,bne a в ряды Фурье. Под--to                          -to становка рядов в уравнение (3) и соответствующее приравнивание коэффициентов дает цепочку рекуррентных формул, из которых находятся все коэффициенты cn :

g 0

c 0    1 - 2 ab 0 ; c n

g _n

1 - 2 ab n

; n = ±1, -2. ^

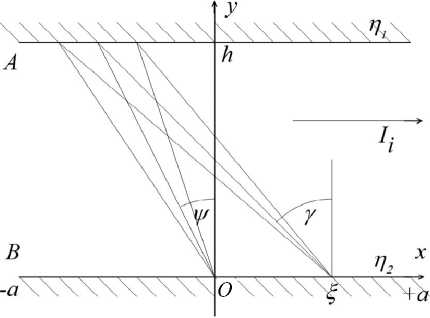
Рис. 1. Схема геометрии ионизатора

Для вычисления эффективности K нам достаточно знать c ₀ . Действительно, суммарная плотность выделения ионов связана с K очевидным соотношением

j = ац .           (4)

1 - a

Интегрируя (4) по длине ионизатора и учиты-+ a вая. что J цd^ = 2ac0. получим выражение для эффективности K в виде

K = ——2 a7g ---;.        (5)

I ( 1 - a )( 1 - 2 ab 0 )

1a1

гДе g о = 2 a j Q ( x ) d x ; b о = 2 a j F ( ⁵ ) d ^{5 .}

a

a

— I

— I

Пусть первичный источник нейтралей изотро-1           (1 — a) I пен, тогда p = — и g0 =  ----— arctg—. Вычис-

π         aπh лим K для трех случаев, характеризующих распределение по направлениям вторичных (отраженных) нейтралей, а именно: изотропного, косинусного и косинусквадратичного. Простые вычисления по формулам (5) дают:

• 1)    f = 1, K 1 = 2 a----- arctg к -----; п          п — 2 ( 1 — a ) arctg к

• 2)    f ( у ) = 2cos у , K ₂ = 2 a ------^-g ^k-

• п — п (1 — a) ,

v    71+к

• 3)    f ( Y ) =—cos² Y , π

• 2.    РАСЧЕТ ПОЛНОГО ТОКА КРУГОВОГО ТЕРМОИОНИЗАТОРА [2]

2 α arctg λ

X( к п — 2 (1 — a) ----+ arctg к

< 1 + к

Во всех случаях к = a)h .

Из сравнения случаев 1, 2 и 3 легко заключить, что K 1 <  K ₂<  K ₃. Какой из них ближе к реальности, можно установить только с помощью экспериментальных данных об угловом спектре вторичных нейтралей либо из достаточно надежной теории отражения.

Работа термоионизатора простейшей плоской конфигурации в режиме полного отбора ионов рассмотрена в разд. 1. Сохраняя общий подход к вопросу (плоские потоки, однородные по координате z ; интенсивности потоков, позволяющие пренебречь столкновениями частиц внутри ионизатора; терминология, введенная в разд. 1), рассмотрим круговой термоионизатор. Цель настоящего раздела — составление и решение уравнений, связывающих потоки частиц (нейтральных частиц — нейтралей и ионов), которыми обмениваются горячие стенки цилиндра радиуса R ; поток нейтралей выпускается в него через очень узкую щель q (см. рис. 2, а); поток ионов, а вместе с ним часть первичных и вторичных нейтралей выводится из цилиндра через щель 5 <  9 <  ^ (дуга AB ).

Пусть поток вводимых первичных нейтралей I имеет угловое распределение p (у), подчиняю-π щееся условию нормировки jp(у)dy = 1. Нейтрали, испарившиеся со стенок, будут иметь угловое распределение f (у) со своим условием нор-π2

мировки j f ( у ) d y = 1; у — угол, отсчитанный

— я / 2

от нормали к поверхности цилиндра (рис. 2, а); вращение против часовой стрелки дает положительный угол, а по стрелке — отрицательный; — п / 2 <  у <  п /2.

Выясним прежде всего характер функций Y ( ф , 9 ) и у ( 9 ) при изменении ф , 9 на отрезке [ 0,2 п ] . Очевидно (см. рис 2, б), что у = 9 /2, 0 <  9 < 2 п ; там же легко заметить, что у ( ф ) при фиксированном θ имеет существенно разрывный характер, что, вообще говоря, осложняет анализ работы ионизатора. Аналитическое представление функции у ( ф , 9 ) :

Y ( ф , 9 ) =

п — (9 — ф) „

Y 1 =----2-----, 0 <  ф <  9 ;

γ ₂

— , 9 <  ф < 2 п . 2

Функция у ( ф , 9 ) имеет непрерывную одностороннюю производную по обеим переменным.

Обозначим плотность выделения нейтралей в произвольной точке стенки Г цилиндра п ( 9 ) , введем также функцию отражения нейтралей:

|1 — a, 9 еГ — uAB, к =

[0, 9 eu AB .

Элементарный поток А Q _вх (входящий в элемент A S ) связан с выходящим потоком А Q _вых очевидным соотношением

А Q вых = к а Q вх . (8)

В свою очередь А Q _вх складывается из потока первичных нейтралей Ip ( у ) А у , пришедших в A S из источника q , и суммарного потока со стороны всей горячей поверхности Г , т. е.

A Q = вых

= к (9) Ip (у )Ау + R |Ау|-jn (ф) f (Y) dф .

Г

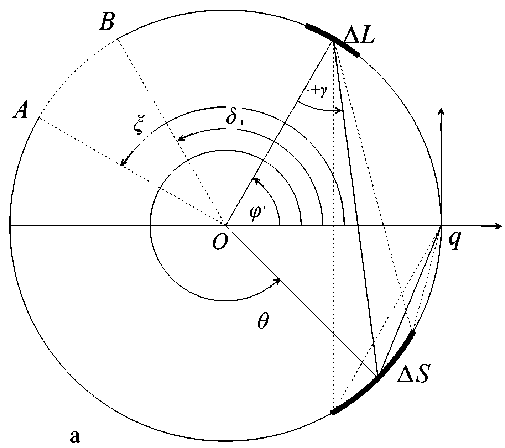
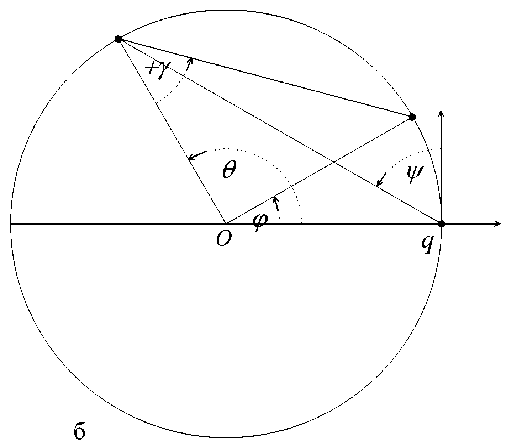
Рис. 2. К расчету потоков частиц в круговом термическом ионизаторе

Разделив (9) на A S¹ = RАб и пользуясь соотно-

шениями п ( в ) = ^d ^ ^вых, d ^ = d W = 1 d S   d θ d θ 2

в пределе

тивности ионизатора K через п ( б ) . Очевидно, что плотность выделения ионов

получим интегральное уравнение

п ( ^б ) = 4k^k( ^б ) Р ( ^ ) + k⁶ \ п ( ф ) f ( У ) ^d Ф . (10) 2 R             2 Г

j = - ^п ( б ) .               (12)

1 - а

Интегрируя (12) по S = 7б вдоль горячей поверхности и разделив на I , получим

В (10) интеграл правой части в силу разрывности функций у ( ф , б ) приходится разбивать на две части; воспользовавшись (6), приходим к основному интегральному уравнению кругового термоионизатора:

и    R Г² П . .       ^     .

^k = 1^' 7 j п ( ^б ) ^{d 6} —И) ^{d 6} .

0 δ

п(б ) =

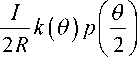
2.1. Случай I (изотропное распределение первичных и вторичных нейтралей)

Исходные данные:

+

^ |jn( ф) f(У1) dФ + j П(Ф) f(У 2) dФ> 2 л                     а

. 0

θ

, (11)

1        1       [1 - а , 0 <  б <  5 , ^ <  б < 2 п ,

—, Р = ~, к = п       п      [   0, 5 < б < ^.

где 0 <  б <  2 п .

Это уравнение принадлежит сложному типу; его удается свести к случаю уравнения Фредгольма с вполне непрерывным ядром в двух случаях: а) f = const; б) f ( п/ 2 + x ) = f ( —П 2 + x ) . Из-за трудности решения уравнения проанализируем два сильно отличающихся случая — изотропное и косинусоидальное распределения нейтралей f .

Предварительно выведем формулу для эффек-

Уравнение (11) принимает вид:

П (б ) =

I

2 πR

(1 - а)

+

+

1 - а 2 π

δ             2π jn(ф)dф+jп(ф)dф

0 δ

что возможно лишь при п = const. Получаем алгебраическое уравнение для η

п =

1 - a i 2 πR

-1

λ a + (1 - a ) п   ,

грал (18) будет

где X = ( ^ - 5 ) /2.

Согласно (13), эффективность изотропного ионизатора будет

ωθ ωθ Q

П = C jSin— + C ₂ cos— + —,      (19)

2        2 α

K = a

1 - X

π

λ, a + (1 - a)—

π

где < y = V a .

По соображениям

= 0, поэтому f = П

симметрии

задачи

d η d θ

• т. е. эффективность изотропного ионизатора не зависит от линейных размеров системы и от взаимного расположения источника q и выходной щели AB .

Численная оценка дает следующие величины:

• а)    y = 0.06 ( AB = 1.2 мм при R = 10 мм),

a = 0.01, K = 0.33;

• б)   y = 0.03 ( AB = 0.6 мм при R = 10 мм),

2.2. Случай II (изотропное распределение первичных и косинусоидальное распределение вторичных нейтралей) .

a = 0.01, K = 0.49.

C , = tg— C 2 .            (20)

Подставляя (20) в (19), находим

П = Q + C cos ^ ( f - n ) ,       (21)

где C =

C 2       _.

cos ( ®П 2 )

Для определения C подставим (21) в (17) и по-

сле интегрирования получим

C = - Q— α

sin—cos — ( n - X ) +

Исходные данные: p I —I — произвольная, дважды дифференцируемая функция; f = ( 1/2 ) cos Y . Для упрощения расчетов совместим выходную щель AB с точечным источником q (положив 5 = X , ^ = 2 п - X ).

Интегральное уравнение (11) принимает вид

λ

+ — cos—sin 2

— ( п - X )

Используя (21) и (22), определим по (13) эффективность

K = 1

λ

-

-

1 - a

•

λω tg^tgy (— - X)

π

π

п ( 9 ) = Q ( 9 ) +

λω

^— tg2 ^{+ a} tgy ( ^{n - X} )

. (23)

Г 9

⁺ P Н п ( ф )

. X

■ ⁹ - ^Ф А , Г \ " ^Ф - ⁹ А sin——d ^ ⁺ J п ( Ф )sin—— iM- (17) ²          2 п - X             ² J

где

Q =

1 - a

2 R

Ip ( ч }; ^P =

1 - a

Особые свойства ядра уравнения (17) позволяют [4] легко свести его к дифференциальному уравнению второго порядка относительно η

Численная оценка дает следующие величины:

• а)    X = 0.06, a = 0.01, K = 0.35;

• б)    X = 0.03, a = 0.01, K = 0.39.

Видим, что эффективность в случае II выше, чем в случае I, но с уменьшением выходной щели нарастает медленнее.

Если принять a = 0.25, то для X = 0.03 получим K I = 0.96 и K I = 0.97 , т. е. при больших коэффициентах ионизации эффективность практически не зависит от диаграммы направленности (функции распределения) испаряющихся нейтралей.

n f +a п = Q 9 +Q            (18)

решение которого всегда можно записать в квадратурах.

1- a

Пусть p = 1/ п , или Q =---- 1 = const; инте-

2 πR