Теория массового обслуживания как инструмент для поиска решений по снижению продолжительности отключений в сельских электрических сетях

Введение. Качественная организация электроснабжения в сельской местности обеспечивает непрерывность работы сельскохозяйственных предприятий, включая производственные процессы и хранение продукции. Перерывы в электроснабжении сельских потребителей могут привести к множеству негативных последствий, которые затрагивают как экономические, так и социальные ас- пекты жизни. Влияние перерывов электроснабжения и их последствий на деятельность сельскохозяйственных потребителей описаны в работах [1–5].

Учитывая значительный износ сельских электрических сетей [6, 7] и уровень аварийности [8–10], одним из путей сокращения количества и длительности перерывов в электроснабжении является грамотно организованная система эксплуатационного обслуживания сельских сетей, требующая комплексного подхода и предусматривающая регулярные проверки состояния оборудования, своевременное устранение аварий и профилактические мероприятия [11, 12].

Применение научных методов при организации системы эксплуатационного обслуживания сельских электрических сетей позволяет определять необходимое количество резервных элементов, исходя из требуемого уровня достаточности и с учетом существующей интенсивности отказов отдельных электросетевых элементов. Также важным аспектом является определение научнообоснованного количества ремонтных бригад, вызываемых из других регионов для оказания взаимопомощи при массовых повреждениях в сельских электрических сетях. Для решения этих задач может быть использован математический аппарат ТМО.

Материалы и методы исследования. Известно, что ТМО изучает системы, предназначенные для многоразового выполнения однотипных задач [13].

Рассматривая процесс использования запасных элементов из резервного фонда, можно считать, что система удовлетворения требований по замене отказавших элементов исправными является обслуживающей системой, а возникающий поток отказов является потоком требований на обслуживание. При этом требование на обслуживание получает отказ, если в резервном фонде отсутствует соответствующий запасной элемент.

Определить вероятность появления ровно m отказов элемента за время t можно по формуле Пуассона [14]:

P?M = (—)- e At,m = 1,2 ..., (1) m\ где Рm(t) – вероятность появления равна m отказов за время t;

m – количество отказов за время t ;

λ – интенсивность отказов.

Вероятность того, что число отказов не превысит количество элементов в резервном фонде, будет равна [14]:

Рт^ = ^=^е-1’   № где Рm≤k(t) – вероятность того, что количество отказов m элементов не превысит число запасных k элементов в резервном фонде за время t;

k – количество элементов в резервном фонде.

Вероятность того, что число отказов будет меньше, чем число резервных элементов, называется достаточностью резервного фонда, и, напротив, вероятность того, что число отказов превысит число запасных элементов, называется недостаточностью резервного фонда.

В такой постановке, задаваясь требуемым уровнем достаточности резервного фонда и зная интенсивность отказов отдельных элементов, можно рассчитать необходимое число запасных изделий. Данный методический подход к определению резервных элементов получил название аналитического метода.

Поскольку в сельских электрических сетях используется как ремонтируемое оборудование, так и неремонтируемое, то при использовании аналитического метода необходимо учитывать следующий нюанс.

Если элемент относится к категории неремонтируемого, то в случае отказа он заменяется на аналогичный элемент из резервного фонда, и в этом случае время t в формуле (2) будет соответствовать периоду пополнения резервного фонда запасными изделиями. Если элемент является ремонтируемым, то при отказе он ремонтируется и затем поступает в резервный фонд. В этом случае время t в формуле (2) будет соответствовать среднему времени ремонта. Очевидно, что чем больше будет интенсивность отказов λ и время t , тем большее количество запасных элементов необходимо иметь в резервном фонде.

На рисунке 1 приведена блок-схема алгоритма для расчета резервного запаса элементов при изменении уровня достаточности от 0,9 до 0,99 при известной величине интенсивности отказов λ и времени t .

Поясним кратко работу алгоритма. В качестве исходных данных в блок 2 вводится следующая информация:

– количество однотипных элементов, эксплуатируемых на объекте – n ;

– интенсивность отказов этих элементов – λ ;

– время – t (пояснение относительно времени, в зависимости от того для ремонтируемых или неремонтируемых элементов производится расчет, было дано ранее).

В блоке 3 рассчитывается математическое ожидание М числа элементов, требующих замены за время t. Поскольку программа позволяет рассчитывать количество резервных элементов при различных уровнях достаточности, то далее организован цикл (блоки 4–12). В 5 блоке вводится вспомогательная переменная S, позволяющая накапливать сумму в соответствии с формулой (2). Перемен- ная k, вводимая в блоке 6, соответствует числу элементов, из которых необходимо сформировать резервный фонд, чтобы расчетный уровень достаточности (в программе для этого используется переменная D) был не ниже заданного Р.

В общем случае разработанный алгоритм позволяет определить число резервных элементов для любого уровня достаточности. Для этого в блоке 4 достаточно изменить параметры цикла.

Математический аппарат ТМО также может быть применен и для расчета необходимого количества ремонтных бригад, которые требуется дополнительно привлечь для проведения аварийновосстановительных работ при массовых повреждениях в сельских электрических сетях с целью сокращения продолжительности отключений.

В этом случае ремонтные бригады можно рассматривать как каналы обслуживания. Повреждения, возникающие в электрических сетях в штатном режиме, устраняются либо силами оперативновыездной бригады, либо бригадой электромонтеров, закрепленной за соответствующим участком электрических сетей. Система функционирует в режиме, когда интенсивность потока заявок на обслуживание λ не превышает производительности каналов μ :

p=^<1 (3)

где ρ – интенсивность загрузки каналов;

λ – интенсивность потока заявок на обслуживание;

μ – средняя производительность каналов обслуживания.

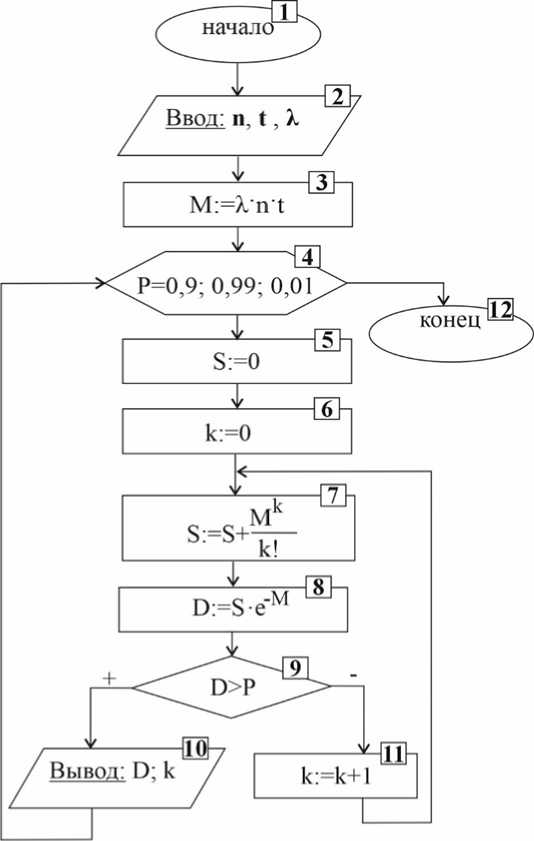
Рисунок 1 – Блок-схема алгоритма для расчета резервных элементов аналитическим методом Figure 1 – Block diagram of the algorithm for calculating reserve elements using the analytical method

При выполнении условия (3), как следует из положений ТМО [12, 13], очередь не растет до бесконечности, и система справляется с входящим потоком заявок на обслуживание.

При массовых повреждениях ВЛ, например, при повышенных гололедноветровых нагрузках, что является нередкостью для сельских электрических сетей, интенсивность потока заявок на обслуживание резко возрастает. Если условие (3) нарушается, то система перестает справляться с входящим потоком требований на обслуживание и вре- мя ожидания в очереди растет, то есть увеличивается продолжительность отключения потребителей. Для сокращения продолжительности отключений увеличивают количество каналов обслуживания – приглашают дополнительные бригады из других регионов для оказания взаимопомощи.

Очевидно, что чем больше каналов будет в системе, тем за более короткий период времени система вернется в установившийся режим, при котором будет выполняться условие (3). Однако, с другой стороны, с увеличением количе- ства каналов их загрузка будет снижаться. Поэтому возникает необходимость в определении такого числа дополнительно привлекаемых бригад, при котором время устранения повреждений будет не более заданного Т, при максимальной загрузке каналов обслуживания.

На рисунке 2 показан алгоритм, позволяющий производить такой расчет.

В качестве исходных данных в блок 2 должна быть введена следующая информация:

• -    число заявок при массовых повреждениях ВЛ – М ;

• -    среднее время обслуживания одной заявки - t_o6 ;

• -    время, за которое необходимо устранить все повреждения – Т .

Предлагаемый принцип расчета основывается на следующих рассуждениях. В общем случае число каналов обслуживания N может изменяться в интервале от 1 до М . При N =1 все заявки обслуживаются одним каналом. В таком случае вероятность выполнить все заявки за время не более заданного Т может быть найдена по выражению [16]:

'Г --=—

^Mto6 (4)

P(0 < t    , ⁽ )

где P (0< t < T ) – вероятность того, что время t не превысит заданное Т .

Очевидно, что коэффициент загрузки k(N) в этом случае будет равен единице. Бригада простаивать не будет.

Если число бригад будет соответствовать числу заявок N=М, то вероятность выполнить все заявки за время не более заданного Т следует определять, используя формулу умножения вероятностей из выражения [15]:

P(O-^06)^M. (5)

В таком случае каждая бригада будет занята обслуживанием одной заявки, а коэффициент загрузки бригад будет определяться как

k(N) = ^. (6)

Вероятность выполнить все заявки за время не более заданного Т , при количестве дополнительно привлекаемых каналов 1< N < M будет определяться на основании формул (4) и (5).

Решением задачи является такое число бригад, при котором вероятность выполнить все заявки за время не более заданного Т и коэффициент загрузки бригад будут иметь максимальные значения. Таким образом, поиск решения связан с необходимостью расчета вероятности выполнить все заявки за время не более заданного Т и коэффициента загрузки бригад для различных состояний системы при изменении числа каналов в диапазоне 1≤ N ≤ M .

Результаты исследований и их о б с уж д е н и е . На основании разработанных алгоритмов были созданы программные продукты [17, 18].

С помощью программного продукта [17] выполнен расчет запасных элементов для включения в резервный фонд для одного из производственных отделений (ПО) электросетевой компании ПАО «Россети». Известно, что на трассах воздушных линий в данном ПО установлено 50000 железобетонных опор, эксплуатируется 150000 изоляторов, 1306 разъединителей и ТП 10/0,4 кВ мощностью от 40 кВА до 250 кВА, на которых в общей

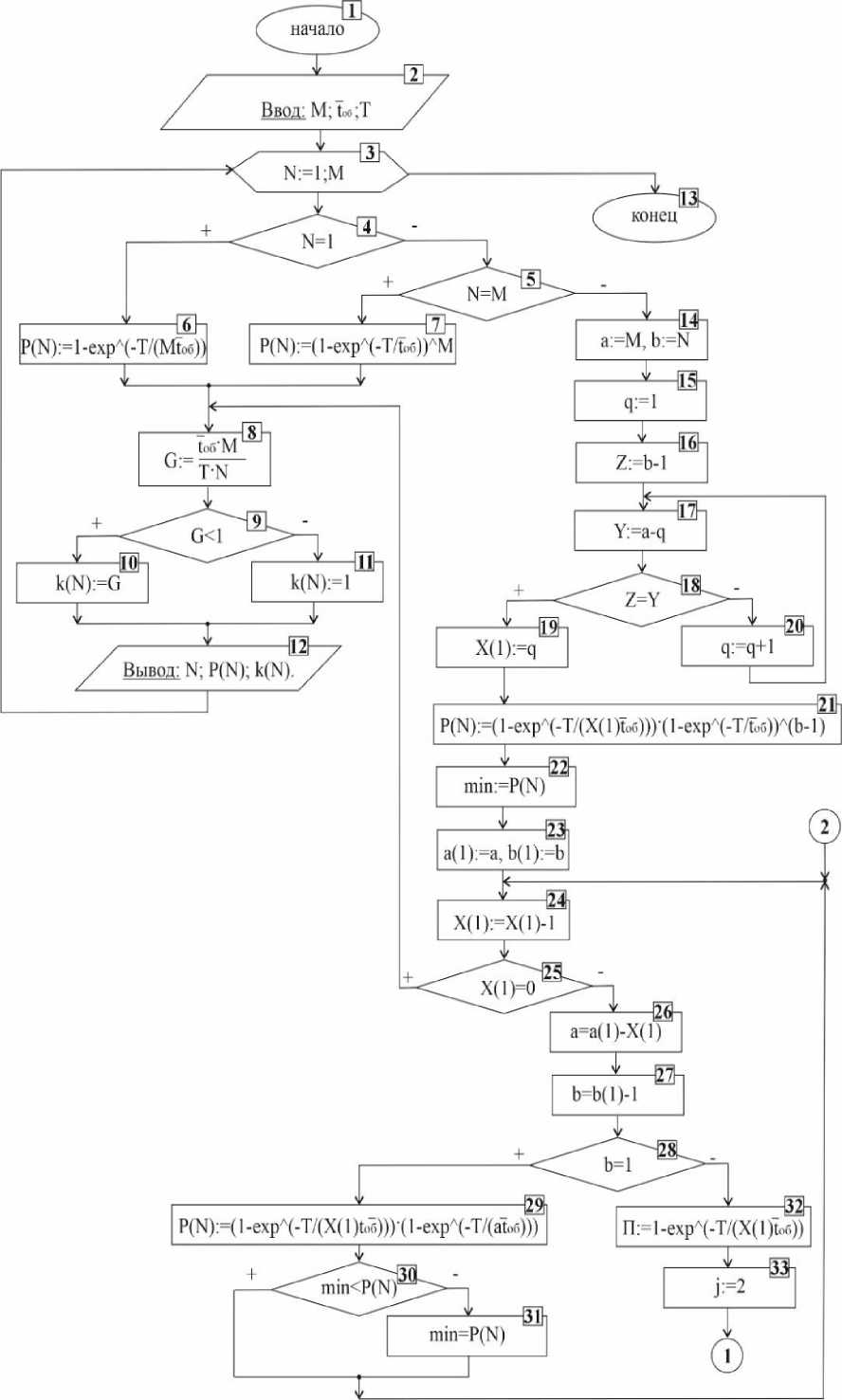
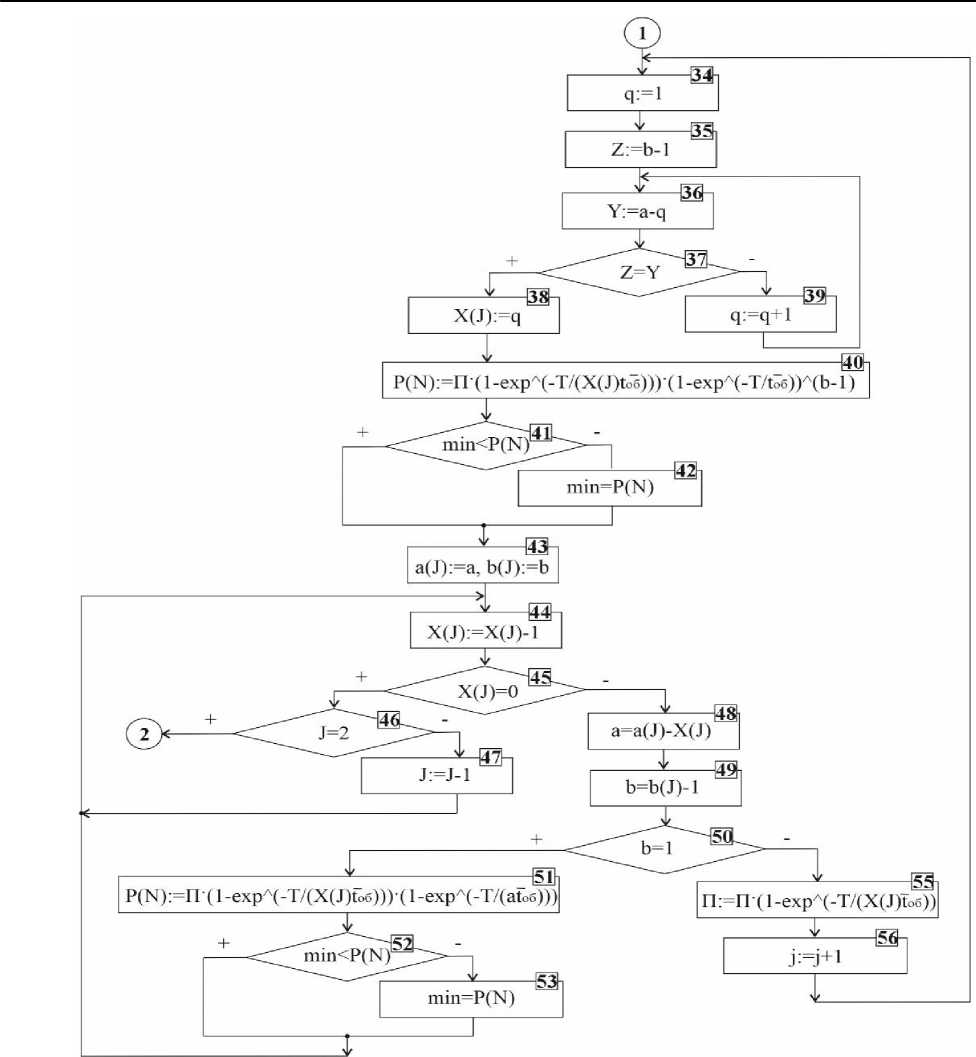
Рисунок 2 – Блок-схема алгоритма для расчета количества ремонтных бригад для проведения аварийно-восстановительных работ при массовых повреждениях в сельских электрических сетях

Figure 2 – Block diagram of the algorithm for calculating the number of repair teams to carry out first responding and restoration operations in the event of massive damage in rural electrical networks

сложности установлено 3915 высоковольтных предохранителей для защиты силовых трансформаторов 10/0,4 кВ, 1306 рубильников и 5220 автоматических выключателей.

Результаты расчета резервных элементов при изменении уровня достаточности резервного фонда от 0,9 до 0,99 представлены в таблице 1.

Таблица 1 – Результаты расчета резервного фонда аналитическим методом при различных уровнях достаточности

Table 1 – Results of calculating the reserve fund using the analytical method at different levels of sufficiency

Достаточность резервного фонда Sufficiency of the reserve fund	0,9	0,91	0,92	0,93	0,94	0,95	0,96	0,97	0,98	0,99
Опоры Pylons	5	5	5	5	5	6	6	6	7	7
Изоляторы Insulators	76	77	77	78	79	79	80	81	83	85
Разъединители Isolators	5	6	6	6	6	6	7	7	7	8
Трансформаторы 10/0,4кВ Transformers 10/0,4кВ	3	3	3	3	3	3	3	4	4	4
Предохранители Fuses	25	26	26	26	27	27	28	28	29	31
Рубильники Knife switches	5	5	5	5	6	6	6	6	7	7
Автоматические выключатели Circuit breakers	13	14	14	14	14	15	15	16	16	17

Для сравнения результатов также был выполнен расчет нормативным методом (таблица 2).

Таблица 2 – Результаты расчета резервного фонда нормативным методом Table 2 – Results of calculating the reserve fund using the standard method

Наименование элемента Element	Норма запаса, шт. Stock level, pcs.		Количество элементов в резервном фонде, шт. Number of elements in the reserve fund, pcs.
	на 100 км по трассе линии at 100 km along the line route	на 100 эксплуатируемых аппаратов КТП per 100 operated devices of package transformer substation
Опоры Pylons	0,25	-	10
Изоляторы Insulators	2	-	80
Разъединители Isolators	-	0,78	11
Предохранители Fuses	-	4,4	58
Рубильники Knife switches	-	0,68	9
Автоматические выключатели Circuit breakers	-	1,55	21

При сопоставлении результатов, полученных аналитическим и нормативным методом, следует отметить, что практически по всем позициям (за исключением изоляторов) при расчете аналитическим методом количество резервных элементов получается меньше, чем при расчете нормативным методом. Для оценки достоверности полученных результатов необходимо проведение дальнейших исследований, связанных со сбором статистического материала о количестве заменяемых электросетевых элементов в данном ПО.

Результаты расчета с использованием программного продукта [18], выполненные для случая, когда количество единовременно поступивших заявок в систему при массовых повреждениях составило М=10, а требуемое время их устранения не должно было превышать Т=24 часа, показаны в виде графических зависимостей на рисунке 3.

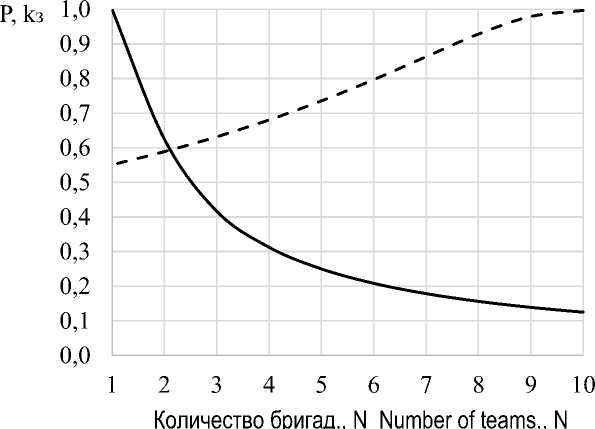
Рисунок 3 – Зависимость вероятности обслуживания и коэффициента занятости от числа ремонтных бригад при М=10

Figure 3 – Dependence of the probability of service and the occupancy rate on the number of repair teams at M=10

kЗ

Р

Из рисунка 3 видно, что при количестве дополнительно привлекаемых бригад N=10, вероятность выполнить все заявки за время не более заданного Т=24 ч достаточно высока (Р=0,997). Однако коэффициент занятости бригад в этом случае составляет 0,13. Это значит, что 87% времени бригады простаивают. Разница между показателями Р и kз составляет 0,867. Уменьшим количество дополнительно привлекаемых бригад до N=6. Разница между показателями уменьшилась, как следует из рисунка 3, в этом случае Р=0,797, а kз=0,21, разница в показателях составила 0,587. При этом коэффициент занятости увеличился почти в 2 раза при незначительном снижении вероятности обслуживания. При количестве бригад N=2 оба показателя од- новременно достигают своего максимального значения Р ≈ kз ≈ 0,6.

Таким образом, с помощью предложенного алгоритма можно подобрать необходимое количество ремонтных бригад и оценить как их загрузку, так и вероятность выполнить все заявки за установленное время.

Выводы. Предложены алгоритмы и программные продукты, позволяющие моделировать процессы формирования резервного фонда электросетевого оборудования и числа ремонтных бригад для проведения аварийно-восстановительных работ в сельских электрических сетях. При разработке алгоритмов использовались основные положения ТМО. Расчеты, проведенные с помощью разработанных программ для некоторых частных случаев, показали следующие результаты.

• 1.    При использовании аналитического метода число резервных элементов при изменении уровня достаточности от 0,9 до 0,99 в подавляющем большинстве случаев получается меньше, чем при использовании нормативного метода расчета.

• 2.    При выборе необходимого числа ремонтных бригад, привлекаемых для проведения аварийно-восстановительных работ при массовых повреждениях в сельских электрических сетях, необходимо учитывать два противоречивых показателя – вероятность выполнения всех заявок за заданное время и коэффициент загрузки бригад. Для рассматриваемого частного случая оптимальным является вариант привлечения двух бригад, при этом Р ≈ kз ≈ 0,6 одновременно достигают своих максимальных значений.