Теория метастабильной кристаллизации переохлажденного эвтектического расплава

Образование метастабильных фаз в сильно переохлажденных эвтектических системах многокомпонентных металлических расплавов вызывает возрастающий интерес в связи с разработкой и освоением промышленного производства аморфных и нанокристаллических металлов, в том числе на крупнейшем производителе таких металлов в России – Ашинском металлургическом заводе [1–3]. Такие металлы обладают уникальными механическими и физическими, в первую очередь магнитными, свойствами.

В традиционных теоретических моделях при описании кристаллизационных процессов в таких системах применяется допущение о локальном равновесии у поверхности растущего кристалла [4, 5]. Однако это допущение оправдано лишь тогда, когда рост кристалла лимитируется диффузионным подводом компонентов из исходного расплава. При этом для определения закономерностей протекания микропроцессов на границе расплав – кристалл используют равновесные диаграммы состояния, характеризующие рассматриваемую макросистему.

При кристаллизации сильно переохлажденных многокомпонентных металлических расплавов рост новой фазы в ряде случаев происходит со столь высокой скоростью, что фронт кристаллизации захватывает атомы компонентов расплава [4]. Поэтому скорости диффузионных потоков при этом не определяют закономерности перемещения фазовой границы. Возникают эффекты, которые не вписываются в обычное понимание закономерностей роста кристаллов. В частности, наблюдается отклонение от условий локального равновесия на границе кристалл – расплав [4–8]. К тому же указанные отклонения имеют нелинейный характер, и для описания системы становятся непригодными методы линейной неравновесной термодинамики. В этой связи в последнее время развиваются новые методы описания таких систем [4]. В качестве одного из направлений таких исследований можно отметить теорию фазового поля [4, 9–13]. Теория описывает переходный слой вблизи растущего зародыша вариационными методами и позволяет учитывать нелинейные эффекты, связанные с захватом примеси. Расчеты позволяют прогнозировать закономерности роста кристалла, а также определять форму растущего кристалла в динамике.

Ранее авторами разработан новый вариационный подход для описания роста кристалла [14, 15]. Преимущества этого подхода заключаются в комплексном описании взаимосвязанных тепловых и диффузионных процессов в системе растущий кристалл – расплав с учетом влияния нелинейных эффектов на границе раздела фаз. В данной работе разработанная теория использована для анализа кристаллизации двухкомпонентного эвтектического расплава при глубоком переохлаждении. Разработанная математическая модель применена к исследованию эвтектического сплава Fe-B, имеющего исключительно важное значение во многих отраслях промышленности. Проанализирован процесс взаимного влияния роста кристаллов зародышей нескольких, в том числе метастабильных, фаз. Построен метастабильный аналог диаграммы состояния системы FeB, позволяющий прогнозировать закономерности роста переохлажденного расплава. Выбор для исследования системы Fe-B обусловлен проблемами оптимизации режима разливки аморфизи-рующихся расплавов на основе железа при получении аморфной ленты в производственных условиях.

1.    Закономерности кристаллизации эвтектического расплава

Для описания роста кристаллов из переохлажденного расплава рассмотрим модельный случай кристаллизации двухкомпонентной эвтектической системы компонентов A и B. Для начала будем предполагать, что при росте кристаллов соблюдается условие локального равновесия. Считаем, что в нашей системе возможно выделение кристаллов чистого компонента A и химического соединения A _n B _n ( n _A и n – соответствующие стехиометрические коэффициенты), которое мы будем обозначать символом Z^E . Символ E будет указывать на соблюдение локального равновесия при росте кристаллов A _n B _n . Рост таких кристаллов лимитируется диффузионным подводом компонентов. На поверхности кристаллов устанавливаются условия, близкие к равновесию. Переход компонентов через границу раздела фаз можно рассматривать как химическую реакцию, скорость которой может быть описана уравнением [16]:

I k = LA ( T )/ T , (1) где I k – мольная скорость образования продукта k на единице площади поверхности раздела фаз кристалл – расплав, A_k – химическое сродство процесса перехода компонента k через границу раздела фаз, L_k – феноменологический коэффициент.

Процесс роста кристаллов A и Z^E при переохлаждении расплава можно продемонстрировать на основе диаграммы состояния рассматриваемой эвтектической системы. На рис. 1 изображен участок эвтектической диаграммы с эвтектической точкой O. Линии A_LO и Z_LO соответствуют равновесию между расплавом и компонентами A и Z^E соответственно. В качестве примера рассмотрим случай моментального переохлаждения расплава эвтектического состава до температуры T 1 . В результате переохлаждения в расплаве могут образовываться зародыши состава A и Z^E . В процессе роста зародыша, например зародыша A, происходит потребление компонента A из близлежащих объемов расплава, содержание компонента A в этих объемах убывает и, следовательно, возрастает доля второго компонента B. Поскольку в системе соблюдается условие локального равновесия, то у поверхности зародыша устанавливается некоторая концентрация c₂ компонента B, близкая к равновесной. Таким образом, линии равновесия могут быть продолжены в область низких температур. Примеры построения таких линий рассматривались вряде работ, например [5, 17]. В нашем случае линии OZ^E и OA являются продолжением линий Z_LO и A_LO и соответствуют значениям концентраций компонентов, которые устанавливаются у поверхности зародышей при локальном равновесии. Между тем, как было указано ранее, в некоторых случаях указанный механизм роста не соблюдается. Для ряда сплавов при их быстром переохлаждении могут образовываться метастабильные зародыши Z , более богатые компонентом A,

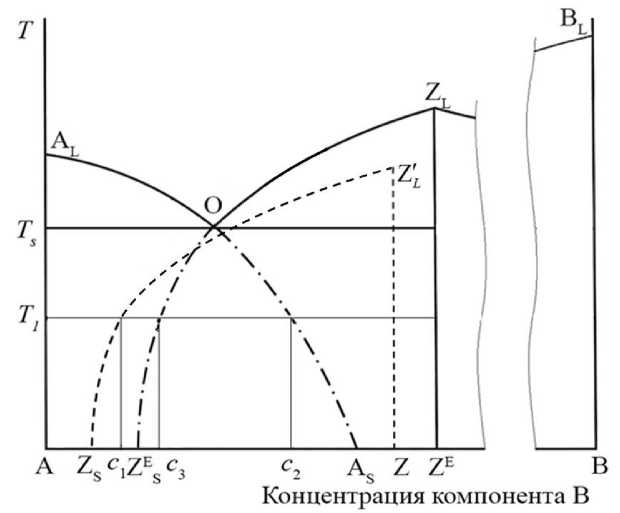
Рис. 1. Модельная диаграмма состояния: линии OZSE и OAS построены при условии локального равновесия между расплавом и фазами ZE и A соответственно; линия Z′LZS отражает изменение концентрации компонентов на поверхности метастабильных зародышей Z в зависимости от температуры T, символы L и S указывают на жидкое и твердое состояния; концентрации с1,c2,c3  соответствуют концентрации компонента B при температуре T1 для соответствующих продолжений линий равновесия следовательно, более бедные компонентом B, чем зародыши ZE . Особенностью таких зародышей является невозможность их образования при обычных условиях относительно медленного охлаждения. Кроме того, такие зародыши могут быть нестабильны при повторном нагреве. В качестве примера таких зародышей можно привести образование метастабильных зародышей Fe3B наряду с зародышами стабильных фаз Fe2B и Fe в быстро переохлажденном эвтектическом расплаве Fe-B [18, 19].

Поясним механизм образования метастабильных зародышей на основе гипотетической диаграммы состояния с эвтектикой, приведенной на рис. 1. Допустим, что при сильном переохлаждении расплава начали образовываться не обычные зародыши ZE , а более богатые компонентом А метастабильные зародыши Z. Если бы при росте у таких зародышей на поверхности соблюдалось условие локального равновесия, то, в соответствии с «равновесной» линией OZSE , на их поверхности образовалась бы избыточная концентрация компонента B. У поверхности зародыша создавался бы слой атомов B, ограничивающих диффузию компонента A к поверхности зародыша. В результате такой зародыш не смог бы расти [4], что и происходит при обычных режимах охлаждения эвтектических расплавов.

Рост метастабильного зародыша фазы Z становится возможным в случае, если концентрация компонента В в нем отклоняется от равновесных величин. Концентрация компонентов у поверхности зародыша соответствует некоторой линии Z ′ _L Z_S (см. рис. 1). Отклонение концентрации компонента В в зародыше может происходить при сильном переохлаждении расплава за счет высокой скорости роста зародыша, когда фронт кристаллизации захватывает исходную фазу и концентрация компонента B на поверхности кристалла снижается. При температуре T ₁ в результате захвата примеси образуется зародыш состава Z, а у его поверхности состав расплава соответствует концентрации примеси В в точке с ₁ [4].

Важно отметить, что в случае образования зародышей Z условие локального равновесия не выполняется, поэтому применение уравнений (1) и использование принципа Онсагера некорректно. В связи с этим в наших предыдущих работах [14, 15] предложена вариационная теория, применение которой к физико-химическому описанию системы зародыш – поверхность раздела фаз – исходный расплав позволяет получить уравнение скорости роста зародыша при отклонении от равновесия. Полученные уравнения могут быть легко преобразованы для случая роста заро- дыша в эвтектическом переохлажденном расплаве.

Для фазы Z выражение мольной скорости образования продукта на единице площади по-

верхности было получено [14,15] в виде

I Z =

( J J JА

I M A xA

J ^J  )d x J К n_A  n_B ) d х J   р^ф dx J / d х J

+

MBxв ) dr J х хJ  хJ J dr  Mz dt /d

BB        АB

где для компонентов A и В: JJ - диффузионный поток компонента на поверхность зародыша, xJ - мольная доля компонента у поверхности зародыша, M - молекулярная масса компонентов расплава и зародыша, r – расстояние от центра зародыша.

При получении уравнения (2) использовалось допущение о сферической симметрии системы зародыш (Ф) - расплав (J). Второе слагаемое в знаменателе отражает вклад нелинейных эффектов, связанных с отклонением от локального равновесия у поверхности растущего зародыша [14]. В случае, если условия у поверхности зародыша приближаются к локальному равновесию, второе слагаемое стремится к нулю. Соответственно, выражение (2) для таких условий запишет- ся в виде

I

E

Z

( Т ^{J      J} Вйх^ К и    и Jch^

А      B x А n А   n B х А

. M A^{x J M}B x B J 5 r Д ^ х ^в ) ^d r

Здесь I _Z^E – мольная скорость образования продукта Z при условиях, близких к равновесным на поверхности кристалла.

2.    Расчет метастабильной диаграммы состояния расплава Fe-B

Приведенное описание закономерностей роста кристаллов в эвтектической системе позволяет сделать расчеты аналогов линий равновесия OAS , OZSE , OZS в области низких температур [17, 18].

В качестве примера выберем диаграмму эвтектической системы Fe-B, являющейся основой для получения ряда аморфных сплавов на основе железа. Эта система на данный момент достаточно хорошо изучена [18, 19]. Расчеты проводили на базе диаграммы состояния, приведенной в работе [19] (рис. 2). При обычном охлаждении расплава эвтектического состава образуются фазы Fe и Fe2B. При скоростном охлаждении ниже температуры 1387 К наряду с этими фазами образуются и метастабильные кристаллы Fe3B.

Для оценки закономерностей протекания процессов в исследуемой системе используем упрощенный метод. Результаты расчетов могут быть далее уточнены, например, с использованием подхода CALPHAD [20] за счет использования дополнительных экспериментальных данных. Примем допущение, что для каждой из кристаллических фаз Fe, Fe 2 B и Fe 3 B изменение стандартной удельной энтропии A s 0 и энтальпии A h 0 при образовании кристаллов не зависит от температуры. Тогда для вычисления константы равновесия для каждой из фаз можно воспользоваться известным выражением [21]

A g ⁰ = Ah ⁰ - T A s ⁰ = RT In K ,                                                        (4)

где K - константа равновесия, A g ⁰ - изменение стандартной удельной свободной энергии Гиббса .

Зная значение константы равновесия K ( T e )_эв в эвтектической точке при температуре T e , найдем изменение удельной энтропии A s ⁰ = A h ⁰ ]Т_е - R ln ( K ( T e ) ) . Подставляя полученное выражение в (4), получим

<Л в ⁰ т-тЛ

K = K ( T _e)„„exp ^^ T e --- .                                                        (5)

V e Ээв       R  TT e J

Необходимые значения параметров для расчета по формуле (5) приведены в табл. 1.

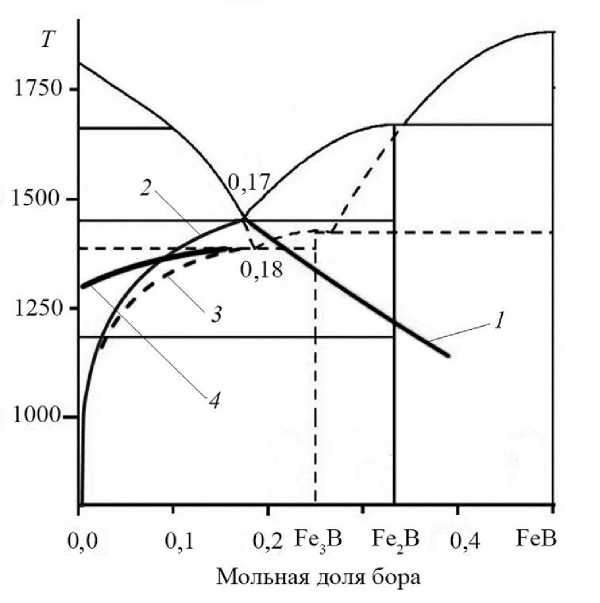
Рис. 2. Модельная диаграмма состояния системы Fe-B с учетом отклонения от локального равновесия на поверхности растущего зародыша. Продолжения линий равновесия в область низких температур: 1 – линия локального равновесия Fe – расплав, 2 – линия локального равновесия Fe 2 B – расплав, 3 – линия локального равновесия Fe 3 B – расплав, 4 – линия, учитывающая отклонение от равновесия для зародышей Fe 3 B

Таблица 1

Термодинамические параметры системы в эвтектической точке

Фаза	Мольная доля бора в расплаве	Температура, К	∆ hF 0 e , кДж/моль	Источник
Fe	0,17	1 452	–12 350	[22]
Fe 2 B	0,17	1 452	–54 470	[23]
Fe 3 B	0,18	1 387	–67 900	[22]

Как отмечалось ранее, для зародышей Fe и Fe2B можно принять условия локального равновесия, т. е. значение концентрации компонента у поверхности зародыша принять равной соответствующей концентрации на равновесной диаграмме состояния на основе формулы (5). Результаты вычислений приведены на диаграмме Fe-B. Расчетные линия 1 (Fe) и линия 2 (Fe2B) являются продолжением соответствующих линий равновесия в область низких температур на равновесной диаграмме состояния. На диаграмме видно, что линия 1 является не совсем гладким продолжением линии равновесия, что обусловлено упрощенным методом (5). Между тем такое упрощение незначительно влияет на результаты. Линия 1 характеризует резкое смещение линии равновесия в богатую бором область, что подтверждается дальнейшими расчетами и известными экспериментами.

Для зародышей Fe3B построим соответствующую «метастабильную» линию на диаграмме состояния, учитывающую отклонения от равновесия. Для таких построений воспользуемся разработанной ранее методикой [15]. При рассмотрении кристаллизации метастабильных сплавов наблюдается, как показали расчеты, незначительное отклонение от равновесия. Соответственно, мольная реальная концентрация бора состояния XB несущественно отличается от равновесной XBE . Поскольку эти концентрации соответствуют концентрациям у поверхности зародыша, то можно разложить мольную скорость образования продукта IZ для зародышей Fe3B вблизи рав- новесия как функцию концентрации компонента, соответствующей диаграмме состояния. Ограничимся членами первого порядка:

IFe3B(XB) = IFe3B +(XB -XB ) ^3  .(6)

Для преобразования полученного выражения нужно учитывать, что при условии локального равновесия на границе раздела фаз можно воспользоваться уравнением линейной неравновесной термодинамики (1). Подставляя (1) в (6), получим

IF BXXb) = Ipe s+(Xfi -XE L~ ^^^ •(7)

Fe B B    Fe B     B    B.

T  д X b

Для дальнейших выводов рассмотрим процесс перехода компонентов из расплава в зародыш как химическую реакцию. В общем виде будем говорить о переходе m исходных компонентов расплава в зародыш постоянного состава (продукт химической реакции). Сродство такой хими-m ческой реакции можно представить в виде A =^ niцJ -цф , где ц - химические потенциалы со-i=1

ответствующих компонентов, n i – стехиометрический коэффициент i -го компонента в реакции.

Далее воспользуемся теорией идеальных растворов, учитывающей влияние поверхностных эффектов на величину химического потенциала зародыша. Тогда можно записать [14]

A = R g T ln s m -v ( P ^ф- P ^J ) ,                                                       (8)

mn где sM = П(xiM) ' K — среднее пересыщение раствора по продукту реакции, xiJ - средняя i=1 Х          / доля i-го компонента в растворе, v - парциальный молекулярный объем зародыша.

Теперь рассмотрим случай равновесного роста. В этом случае у поверхности растущего зародыша устанавливается локальное равновесие. Следовательно, из (8) можно записать RTlns-v(Pф-PJ) = 0, где е - пересыщение раствора у поверхности зародыша при условии равновесия. Используя это соотношение в (8), получим выражение для условия равновесного роста

A = RT ( ln s _M

—

m lns) = RTIn П((xiM)'/(   ) I .

V i = 1 ^V                   ^7

Перепишем полученное выражения для случая роста зародышей Fe 3 B. Поскольку разница

TV ci - ciM для каждого из компонентов является малой величиной, получим

A

RT

( ^хвм

Tf 3"

^{Х в} ) rT.  1-rT,

V ^хв м   ^{1 х}в м 7

При локальном равновесии х J = X BE , можно переписать (7) с учетом (1) и (10)

I ^Fe3^в _ 1   ^XB  ^Xв

ТE   1   X^е - J

I Fe₃ B      X B  ^XB M

Теперь применим выражение мольной скорости IFe B для реального роста метастабильного зародыша Fe3B (2) и выражение мольной скорости IFEe B при равновесном росте. Подставляя уравнения (2) и (3) в (11), а также применяя уравнение Фика и стационарное выражение для градиента концентрации [14], можно окончательно записать

^XBE  ^XB = 2 ^vJ M B р Ф ⁿFe^XB ⁿB^XFe ¹

^XE ^{- x J} M     ^M К    M B X B ⁺ M Fe X Fe ^ F e M ^{- X}Fe

Полученное выражение позволило рассчитать продолжение линии равновесия в область низких температур при отклонении от равновесия. Расчеты продолжения линии равновесия Fe3B при условии отклонения от локального равновесия проводились методом Ньютона на основе уравнения (5).

Как видно из графика, «неравновесная» линия 4 Fe 3 B (см. рис. 2) существенно отклоняется от «равновесной». Эффект отклонения линии Fe 3 B от равновесных значений определяется повышенной скоростью роста кристаллов. Для роста зародышей Fe 3 B требуется в полтора раза больше железа, чем для зародышей Fe₂B, и не требуется большого количества бора. В исходном эвтектическом расплаве Fe 83 B 17 концентрация бора существенно меньше концентрации бора в зародыше Fe 2 B. Поэтому рост кристалла Fe 2 B лимитируется диффузией бора к поверхности зародыша.

Для атомов Fe 3 B, очевидно, наблюдается совершенно другой механизм роста. Концентрация бора в зародыше не столь существенно отличается от концентрации в расплаве по сравнению с предыдущим случаем. Кроме того, одновременно с ростом зародышей Fe 3 B происходит рост кристаллов Fe и Fe₂B, что способствует увеличению концентрации бора в расплаве. В результате в расплаве образуются зоны, в которых мольная доля бора достигает доли в зародыше Fe 3 B. Образование таких зон способствует росту зародыша со скоростью, превышающей диффузионный подвод компонентов из расплава в соответствии с эффектом бездиффузионного роста. Фронт кристаллизации захватывает атомы бора.

Такое понимание механизма роста зародышей Fe 3 B подтверждается экспериментальными исследованиями, которые показывают, что зоны метастабильных кристаллов Fe 3 B представляют собой вкрапления в формирующуюся эвтектическую структуру кристаллов Fe и Fe₂B [24].

3.    Моделирование кристаллизации переохлажденного расплава системы Fe-B

Разработанная метастабильная диаграмма позволила провести моделирование кристаллизации переохлажденного расплава Fe–B. Для построения модели использовали разработанную ранее методику [5]. Обобщенная модель оценивала вероятность зарождения кристаллов Fe, Fe 2 B и Fe 3 B. С учетом уравнения (2) и диаграммы состояния (см. рис. 2) рассчитывались скорости роста кристаллов для всех возможных размеров. Распределение кристаллов различных размеров рассчитывалось в реальном времени протекания процессов. Тем самым была реализована макромодель протекания процесса кристаллизации расплава в объеме. Одновременно модель позволяла проследить закономерности роста каждого отдельного кристалла.

Полученная математическая модель включала следующие основные уравнения:

• ■    уравнения интенсивности образования зародышей Fe, Fe 2 B и Fe 3 B [5]:

Ji = N о P i ( q KPi )_x G²- exp f^{- A} G i ( ^qKPi ) ^ ,                                                  (1³⁾

2n    ^     kT J где qКР – число молекул в критическом зародыше, k – постоянная Больцмана, T – температура, AG(q) - изменение энергии Гиббса при образовании зародыша из q молекул, G2 - вторая производная от AG (q) для критического зародыша, p - вероятность присоединения частицы к по- верхности критического зародыша, N0 – исходное число молекул в растворе.

• ■    уравнения распределения частиц для каждого типа зародышей Fe, Fe 2 B и Fe₃B [5]:

8-N +^'-0,(14)

d td bFe ( t, q ) = ^^RNADFT ( xFem - xFe ),

V x*

К G           DFe MBxB + MFexFe i yJ   yJ \/in bFe2B (t,q) = 4nRNA —  J  g—J   E J (xFe M  xFe) -

MBV   nFeXB - nBXFe bFeB (t, q )= 4nRNA-DF^ (MBxL+MFexFe}. (xFeM - xFe) + 8^rNa P^DFe,(17)

• 3              MB V    nFe хв - Пв XFe  X         ’

где N(t,q) – плотность распределения зародышей по размерам, v – удельный объем зародыша, D - коэффициент диффузии, N А - число Авогадро, x ^J - средняя доля компонента в растворе, е - пересыщение раствора по соответствующему компоненту, b - скорость роста частицы

(выражения b_Fe и b_{Fe B} получены в работе [5], скорость роста b_{Fe B} метастабильной частицы получена в работах [14, 15]).

• ■ уравнения баланса компонентов системы [5]:

^                   ^^

N Fe ( t ) = N исх ( 1 - с 0 ) - J N Fe ( t,q ) qdq - n Fe  J   N Fe 2 в ( t,q ) qdq - n Fe  J   N Fe 3 в ( t,q ) qdq , ⁽¹⁸⁾

q ГFe                          q ГFe ₂ B                            q ГFe ₃ B

^^

NB (t )=Nисхс0 - nB J NFe2в (t, q) qdq - ns J NFe3в (t, я) qdq, qГFe2В                          qГFe3В где Nисх – исходное количество молекул, NFl e и NВl – оставшееся их количество.

Расчеты проводили для расплава эвтектического состава Fe 83 B 17 . Уравнения математической модели решали с использованием разностных методов. Для решения уравнений разработан комплекс программ на языке С++. При проведении расчетов использовали следующие исходные данные [5]: энергия активации диффузии бора в расплаве Fe-B – 80 000 Дж/моль, межфазное натяжение (для зародышей железа в расплаве Fe-B) – 0,204 Дж/м², межфазное натяжение (для зародышей Fe 2 B и Fe 3 B в расплаве Fe-B) – 0,3 Дж/м².

На первом этапе расчетов вычисляли изменения критического размера и интенсивности зарождения зародышей. Расчет показал, что при охлаждении в интервале температур 1100–1200 К интенсивность зарождения зародышей фазы Fe₃B весьма низкая (рис. 3а). В этом температурном интервале преобладает образование и рост зародышей фаз Fe и Fe 2 B, что подтверждается результатами экспериментов [24]. Причина этого эффекта наглядно следует из построенной метаста-бильной диаграммы состояния (рис. 2). При небольшом переохлаждении ниже эвтектической точки 1 387 К для роста зародышей Fe 3 B недостаточно атомов бора. При дальнейшем переохлаждении «метастабильная» линия (линия 4) резко уходит в сторону уменьшения концентрации бора, что способствует увеличению интенсивности зарождения зародышей Fe₃B.

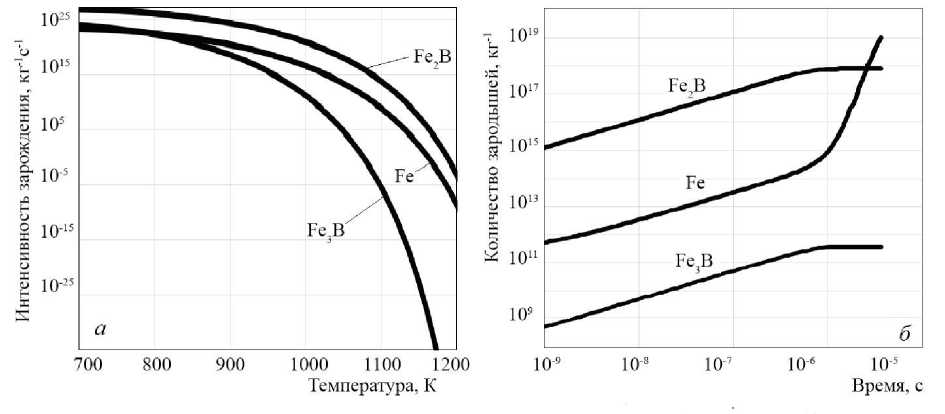
Рис. 3. Изменение интенсивности зарождения зародышей в зависимости от температуры (а); изменение количества зародышей в 1 кг расплава от времени протекания процесса при температуре 900 K (б)

При дальнейшем переохлаждении расплава в интервале температуры 1000–1100 К интенсивность зарождения кристаллов Fe₃B быстро растет. При более глубоких переохлаждениях интенсивность зарождения фазы состава Fe₃B приближается к интенсивности зарождения фазы Fe и Fe 2 B. На этом этапе наблюдается активный рост всех трех фаз. Между тем, несмотря на то, что интенсивность зарождения фазы Fe 3 B меньше, чем интенсивность зарождения фазы Fe 2 B, скорость роста зародышей фазы Fe 3 B существенно выше скорости роста зародышей Fe 2 B, что подтверждает сделанное выше предположение об особом механизме роста зародышей Fe 3 B. К примеру, дополнительный расчет при моментальном переохлаждении расплава до температуры 1000

К показал, что увеличение количества молекул в зародыше в секунду для околокритического зародыша составляет: b_Fe =1,07·10¹⁰, b_{Fe B} = 7,79·10¹⁰, b_{Fe B} = 4,01·10¹¹.

На втором этапе проводили расчет изменения количества зародышей в зависимости от времени при температуре 900 K. Расчет показал, что при таком переохлаждении наблюдается активный рост всех зародышей независимо от их состава, что также соответствует результатам экспериментов [24]. На последних этапах кристаллизации раствор обедняется бором, что приводит к более активному росту кристаллов железа.

Выводы

• 1.    Разработана новая вариационная теория кристаллизации переохлажденных эвтектических сплавов. Теория позволяет прогнозировать закономерности кристаллизации переохлажденных эвтектических сплавов при различных условиях, обеспечивая экономию затрат на проведение дорогостоящих экспериментальных исследований.

• 2.    Построена метастабильная диаграмма состояния расплава Fe-B. Изучено влияние метаста-бильных эффектов на рост кристаллов. Получены зависимости концентрации компонентов у поверхности кристаллов от температуры как для стабильных кристаллов Fe и Fe 2 B, у которых наблюдаются условия локального равновесия у поверхности растущего зародыша, так и для мета-стабильных кристаллов Fe₃B, рост которых обусловлен эффектом захвата примеси.

• 3.    Проведено математическое моделирование зарождения и роста кристаллов в переохлажденном эвтектическом расплаве Fe 83 B 17 . Показано, что в переохлажденном расплаве наблюдается одновременное зарождение и рост стабильных фаз Fe и Fe₂B с метастабильной фазой Fe₃B. Изучены закономерности зарождения и роста метастабильной фазы Fe 3 B. Показано, что механизм роста зародышей Fe 3 B принципиально отличается от роста зародышей Fe и Fe 2 B вследствие бездиффузионного захвата растущей поверхностью кристаллов Fe 3 B атомов бора, а скорость бездиффузионного роста околокритических зародышей фазы Fe₃B превышает скорость роста зародышей Fe и Fe₂B.

• 4.    Рассчитанная метастабильная диаграмма состояния системы Fe-B позволяет прогнозировать закономерности отвердевания и кристаллизации переохлажденных расплавов при получении аморфных металлов в производственных условиях.

Исследование выполнено при финансовой поддержке РФФИ и Челябинской области в рамках научного проекта № 20-48-740034.