Теория моделирования операционной последовательности сборки и монтажа объектов авиационного производства

Коптев Андрей Анатольевич, индустриальный директор ческой документации, то необходимо пооперационные этапы обеспечивать управляемыми процессами анализа ситуации, принятия решений и формирования команд в информационной системе для стабилизации устойчивости производства.

Распечатки карт технологических процессов являются исходной информацией в таких условиях, где непрерывный управляемый процесс представляется как дискретный по переходам и операциям. Проблема заключается в правильном выборе и постановке задачи оптимизации для обеспечения требуемого решения и его точности достаточной.

Так как общий граф сборочного пространства является его моделью, то в областях допустимых вариаций параметров топологических схем взаимосвязанных процессов применимо рекуррентное уравнение Беллмана:

F_t - i ( X - i ) = max { fi ( ^хи , X ( U j ) ) + F_t ( X ( U j ) ) } , i = 1,2...., n , (1) где F - функция качества перехода, и F_n ( x_n ) = 0

Для обеспечения процесса шаговой оптимизации ТП вводим ограничения на множество допустимых путей переходов состояний в виде дуг графа как множества решений соответствующих задач. Узлы, сгруппированные по уровням, соответствующим шагам переходов, образуют множества x ₀, x ₁,..., x_N , где x ₀ и x_N содержат по одному узлу. Параметры дуг рассчитываются по специальным алгоритмам для исследуемых множеств.

Такой подход является одним из эффективных путей решения задачи проектирования конкретной производственной деятельности при представлении сборки в виде модели, как ориентированного графа.

В рамках решения этой задачи выбора оптимального по ряду критериев проекта ТП в работе рассматривается выбор, оценка и синтез последовательности операторов преобразования сборочно-монтажного пространства.

В задачах проектирования ТС необходимо совместить аналитическую взаимосвязь между параметрами уравнения и параметрами решения, одновременно с этим выразить эту взаимосвязь в виде алгоритма управляющих воздействий на системы разного рода. Таким образом, можно совместить в параметрическом виде исходное уравнение и его решение, получив параметрическую структуру, изменение которой с течением времени анализируется для получения оптимального параметрического пространст-ва решений, в котором выбираются устойчивые состояния ТП.

Рассмотрим параметрические формы a i ( A i , A ₂, t ) и a 2 ( A 3 , A 4 , t ) , описывающие состояния ТС:

*                         *2

wb(t) = Ai + A 2 wb(t);w*(t) = A3 - A4 w*2(t),

*                                                                          ...*

где w_b – динамика выполнения операции; w – динамика подготовки производства для выполнения операции; А₁ – параметр ресурсов; А₂ – параметр эффективности; А₃ – параметр, характеризующий индекс качества операции; А₄– параметр, характеризующий неустойчивость по некоторому критерию операции (фактор рисков).

Уравнение, описывающее состояние ТС, представляет частный случай уравнения Риккати, которое в первом приближении решается в квад-ратурах, причем считаем, что w(t) и w_b(t) -наблюдаемые фазовые координаты соответствующих векторов состояний в начале или в кон-це фиксированного промежутка времени наблюдений за группой a ( A_x , A ₂, t ) , a 2 ( A 3 , A 4 , t ) .

В качестве достаточных приближений значений для w(t) и wb(t) в детерминированных условиях процесса выбираем:

wU t ) = tg ( V Ai A 2 t)

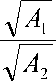
w * (t) = th ( ^ A 3 A 41)

(3) ;

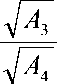
Решения уравнений (1)-(2), полученные для wb(t) и w(t) , удовлетворяют аналогичным уравнениям (3)и(4) в определённой метрике t.

При более точных условиях измерения фазовых координат wb(t) и w(t) в этом случае исходные уравнения имеют вид :

*

••

•

W b ( t ) = A 1 + A ₂ W 2 ( t ) + A ₅ sin[ w b ( t ) t + ф _{ь 0} ] a ( t ) -

• •*

^{- A} 5^cos[ w b ⁽ t ) t + Ф ь 0^] P ⁽ t );

*

II

I

• •II

w ( t ) = A + A 4 w *²( t ) - w b ²( t ) A + A ₇sin| w *( t ) t + ф ь ₀] a ( t ) -

*            I.*

^- A ₇c ^{os[ w ( t} )t +Ф _Ь 0 ^] P ^(t ),

* где a ( t ) - функция, учитывающая характер поставки материалов и комплектующих, изменения конструкторско-технологической информации и др. полученная после подстановки w_b ( t ) и w ( t ) в уравнение, описывающее характер коле

*

баний по a ; р ( t ) — функция, характеризующая поставки для последующих процессов сборки при установленной их ритмичности ,получа-емая после подстановки w b ( t ) и w ( t ) в уравнение динамики колебаний по в ; A 5 - параметр, характеризую-щий устойчивость операции при межцеховых колебаниях объёмов и номенклатуры поставок материалов и комплектующих, А₆ – параметр, характеризующий степень освоения в цехе указанных сборочных процессов. А₇ - параметр, учитывающий возможные переналадки и переустройства рабочих мест исполнителей, Ф ь о - начальная фаза сезонных изменений.

Сгруппировав слагаемые ряда в уравнениях (5)-(6) по степеням t : t , t³ ,■■■, , получаем несколько уровней классификации состояния системы ТП. Получение реше-ния в виде ряда по степеням t определяет, какие параметры влияют на форму кривых w b ( t ) и w ( t ) , одновременно формируя управляющее воздействие для получения нужных форм w b ( t ) и w ( t ) . Процессы оптимизации ТС определяют производственную стратегию сборочных процессов. В инвариантной ТС итерационный процесс поиска экстремума связан с заданием соответствующих начальных условия в дифференциальных соотношениях, выражающих баланс основных процессов, причем параметрически изоморфных. Параметрический изоморфизм ведет к новым классификациям и описанию конечномерных представлений. Получаем дискретные функции состояния ТС разложением в ряд базовой целевой функции по базисным векторам, причем коэффициенты разложения являются собственными значениями линейного оператора ( Л 1 , Х ₂ ,„; X n ), которым соответствуют вероятностные представления, рассчитываемые как плотности вероятностей такого состояния. Изображение оригинала заданной вероятности в комплексной области рассчитывается как

у!

(Р + X) n+1

где s – количество факторов и их выборочных значений в распределениях-композициях, ; р – комплекс-наявеличина; X — параметр-статистика, выражающий собственные значения линейных операторов, которые при преобразованиях технологического пространства сборки должны соответствовать условиям постановки задачи.

Применим линейный оператор W к вектору x и получим образ y= A ( x ) вектора x . Можно показать, что каждому линейному оператору A в некотором базисе пространства Rn соответствует матрица А, по которой можно пересчитывать любой вектор в его образ в этом же базисе. Иными словами, любой линейный оператор можно задать в некотором базисе соответствующей матрицей: матрицей оператора A в базисе {ek}. Фор-

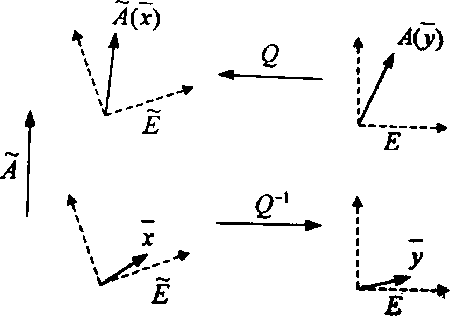
Рис. 1. Тензорное преобразование сборочномонтажного пространства агрегатов летательных аппаратов

мула пересчета имеет вид: y = A ( x ) = x .

Инвариантность тензоров и тензорных функций относительно ортогональных преобразований cборочно-монтажного пространства обеспечивается тем, что ортогональные тензоры вида Q: Е — л^- ^ Е осуществляют повороты и зеркальные отображения, сохраняя при этом длины векторов, углы между ними и переводят один ортонормированный базис в другой. Определим понятие инвариантности тензора А: Е — л- ^ Е относительно ортогонального тензора Q: Е ——^ Е .

Определение 1. Тензор А называется инвариантным относительно тензора Q, если А удовлетворяет равенству

А = Q o A o Q ^{- 1}            (7)

Уточним геометрический смысл этого понятия. Пусть Q – ортогональный тензор, осуществляющий поворот любого вектора в пространстве E(dim E=3) на заданный угол вокруг оси, ортогональной плоскости чертежа (рис. 1).

Будем считать, что Q действует из пространства Е в пространство Е , где Е соответствует некоторому технологическому преобразованию на дуге графа системы как в модели, или технологической операции на рабочем месте. Рассмотрим пространство, в которое оператор Q: Е —л^- ^ Е переводит пространство Е. Обратный оператор Q^-1 : Е — л ^- ^ Е возвращает пространство Е в исходное. Пусть на пространстве Е задан тензор А: Е —л- ^ Е .Допустим, Е -подпространство сборки после i-го технологического перехода. Определим в этом пространстве такой тензор А : Е__ ^л- >   Е , который оказывал бы на любой вектор х е Е такое же действие, которое оказывает тензор А на прообраз вектора х (т.е. на вектор y = Q^-1 (x) ) в пространстве Е. Искомый тензор А должен удовлетворять равенству (рис. 1)

V x е Е А(х) = Q(A(y)) = Q(A(Q^-1(x))) , которое эквивалентно тензорному равенству

А = Q o A o Q ^{- 1}             (9)

Определение 2. Отображение F: Ј(Е)> Ј(Е), связанное с функциональным преобразованием элементов сборочных позиций на производстве, инвариантно относительно ортогонального тензора Q е J(Е), если оно удовлетворяет равенству V A е J(Е) Q o F(A) o Q ^{- 1} = F(Q o A o Q ^{- 1}) .(10)

Определение 3. Отображение F: Ј(Е)> Ј(Е) инвариантно, если оно инвариантно относительно любого ортогонального тензора Q е J(Е), т.е.

для любого ортогонального Q е J(Е), для V A е Л^Е)

Q o F(A) o Q ^{- 1} = F(Q o A o Q ^{- 1}) .   (5)

Задача состоит в схеме введения функциональных аргументов в предикаты, причем за каждый переход число аргументов увеличивается на единицу. Например, добавляем третье место в двухместный предикат Р введением нового аргумента, называемого переменной состояния, получаем последующий предикат более высокого порядка:

P(x, y) > P(x, y, s).               (6)

Рассмотрим в некотором абстрактном сборочно-монтажном пространстве переменную состояния, которая может принимать значения s1, s2, s3… s10… sN. Эти состояния характеризуют определенную реализацию связей в узле, которая приводит к реализации сборок компонент с новыми свойствами, к возникновению последующей структуры сборок. При этом повышается устойчивость складывающихся взаимодействий между компонентами и дискретными сборками этих компонент. Таким образом, происходит процесс связывания компонентов в узлы, а их, далее, в более сложные устойчивые сборки, моду- ли, свойства которых согласованы с их местом в некотором агрегате, системе.

В свою очередь, такой процесс характеризуется определенными состояниями, которые связываются посредством различных операторов. Тогда этот процесс может быть формализован в виде графа, в котором состояния s1, s2, s3… s10… sN связаны операторами F1, F2, F3... FN

Оператор F1, означает переход из состояния s1 в s2 в результате действия оператора F1.

Эти действия легко представить в исчислении последовательности операторов преобразования, так как эти операторы являются отображаем состояния в состояние. Результаты применения таких операторов можно подставлять на место переменной состояния, аналогично подстановке простой переменной. Например Р (x1, F(s)) вместо Р(x,m). Уточним такие теоретические аспекты представлений и преобразований сборочных пространств в соответствии со своими функциями распределения эффективности действий.

Также из сказанного выше определим исчисление количества и последовательности операторов преобразования и обозначим в требуемом системно-функциональном пространстве сборки в виде:

R = (P i , F S k , a m , A n ). (7)

Она состоит из множества предикатов, которое обозначено Р, множества операторов, обозначенного F, далее, безусловно, множества состояний S. затем системы аксиом, обозначенной через a, и, наконец, множества объектов, обозначенного через А, в которое входят не только объекты монтажа, но и исполнители. Поясним более детально содержание каждого отдельного символа в R. Принимаем, что отображения Fz, 1, z , является линейным (гомоморфизмами), для всех x, y, g, R". Также применение линейного оператора Fk вектору 7 дает образ y = F(x) вектора х , то есть отображение линейного пространства Rn в аналогичное Rm можно доказать, что каждому оператору F в некотором базисе пространства Rn соответствует матрица оператора ^ .в базисе {e k }. Формула пересчета y = F(x) = x Предикаты, т.е. выражения, обладают тем свойством, что, приписав значения переменным х,у,... из соответствующих областей определения, мы получаем логические высказывания при формализации действий исполнителя. Для записи выражений используются предикатные буквы Р, Q. и т.д., дополненные указанием аргументов. При этом выражения могут быть истинными или ложными, как это принято во всех формализмах исчисления предикатов первого порядка. Операторы переводят состояния в состояния, а аксиомы “a” представляют систе- му аксиом специального вида. Аксиомы преобразования сборочно-монтажного пространства – это не произвольные, правильно построенные формулы исчисления предикатов, а формулы одного из двух типов. Один тип аксиом таков:

P r ( x , A i ) • ( P ( x , A i ) = A ₂) ^ Q ( x , A ₂) , (8) где PQ _e P F e F, S 1 ,S₂ e S.

Эти аксиомы могут быть записаны в более общей форме. Однако, можно считать, что эти аксиомы имеют следующий смысл: для того, чтобы применить оператор F в ситуации S1, прежде всего необходимо, чтобы выполнялось условие P , т.е. это начальное требование для применимости оператора F. Теперь, после применения оператора F, полученное состояние характеризуется предикатом Q. Под буквами Р и Q в приведенных записях мы будем иметь в виду, что эти символы обозначают подмножество множества предикатов Р. Так например, начальное условие Р может быть длинной конъюнкцией предикатов Р = Р1, Р2... Рn, которая полностью характеризует все условия применения оператора F в ситуации S1. Таким образом, Р – это своего рода начальные условия, а Q - конечные условия по отношению к оператору F. В общем виде, т.е. независящими от конкретного состояния S1, аксиомы могут быть записаны следующим образом:

V A { P ( x , A ) ^ Q ( x , F ( x , A )) } , (9) где мы воспользовались подстановкой F(х,S) вместо S₂, тем самым исключив обозначения двух конкретных состояний. В этом выражении S соответствует начальному состоянию S₁, а F(х,S) – конечному состоянию S₂.

Для определенности процесса преобразований необходимо точно описать начальную ситуацию для того, чтобы можно было применять те или иные аксиомы. Для описания начальной ситуации используются схемы аксиом вида:

D(x, S_H), (10) где D e P S H e S, x e A.

В этом случае S_H – конкретное начальное состояние, х – элемент множества узлов, А – константа, имеющая существенное отношение к начальной ситуации. Для начальной ситуации предикат Р не обязательно будет двухместным предикатом. В общем случае он может быть произвольным n-местным предикатом с любым числом аргументов. Таким образом, каждому конкретному условию соответствует целый ряд получаемых соединений узлов-констант; в свою очередь D может представлять собой последовательность конъюнкций такого рода предикатов. Сформулировав теперь задачу в формальной записи, решаем вопрос, существует ли конечное состояние S, дл k я которого выполняется условие A ^{( x} , A k ) ^ ^ A i , или

( E l A k ) { A ( x , A k ) } ; (11)

Sk = F1 (x, F2 (x, … , Fn-1 (x, Fn (x, SH ) ) … ) ) = = F1·F2 … Fn (x, SH). (12)

Таким образом, решение задачи, поставленной в исчислении последовательности операторов преобразования, имеет вид (12).

Определим предикаты, операторы, состояния, аксиомы и множество объектов. Подход к решению задач в исчислении последовательности операторов преобразования состоит в формировании такого подхода к исследованию проектов ТС, чтобы априори можно было оценить трудоемкость вычислений и разрешимость, не решая все задачи непосредственно. Следовательно, действия в исчислении последовательности операторов преобразования несколько отличаются от прямого подхода к решению логических задач. Когда задача поставлена в такой форме, в силу полноты логического исчисления первого порядка мы можем гарантировать, что решение ее будет найдено. Для конкретного примера. определим предикаты для модели сборки узла. Сначала выбираем первый предикат – предикат “ находится”:

Р = { находится (х, у, S) }. (13)

Предикат верен, если только х находится вместе с у в состоянии S. Множество допустимых операторов ограничивается всего одним оператором – оператором “установка ”в приспособлении или стапеле, допустим, двух элементов сборки.

F = { установка (х, у, r1, r2, S)}. (14)

Здесь “х”– исполнитель, осуществляющий действие, определяемое этим оператором, и состоящее в выполнении подготовительного перехода сборочной операции. В общей схеме производства формируемые состояния образуют множество:

S = { S1, S2, …, Sn }. (15)

В свою очередь, множество объектов сборки А состоит формально из

{ И, b1, b2, h1, h2, R}, (16) где И – исполнитель или автомат, выполняющий установочный переход;

b1 и b2 – константы, которые мы вводим для обозначения имен устанавливаемых элементов; буквы h1 и h2 фиксируют начальные положения этих элементов, т.е. b1 находится в h1, а b2 – в h2. Зададим аксиомы, определяющие исходные, первоначальное положение элементов:

a i : находится ( b i , h i , S h ) a ₂ : находится ( b ₂ , h ₂ , S_h)

Теперь зададим аксиомы, описывающие ус- тановку элементов, а также возможности и условия такой установки.

Аксиома для этой цели может быть задана следующим образом:

α 3: ( ∀ S, х, r₁, r₂) { находится (х, r, S) ⇒ находится (х, r₂ сдвиг (Э, х₁, r₁, r₂, s)) }.         (18)

Эта аксиома фиксирует тот факт, что каковы бы ни были состояния S, объект и положения r1 и r2, то если исполнитель х изменяет положение элементов из r1 в r2, возникает состояние, в котором х будет находиться в r2.

Сформулируем и решим вначале простую задачу монтажа, а затем перейдем к более сложным задачам.

Пусть первая задача сформулирована так: ( ∃ S_k1) { находится ( b₁, R, S_k1) }.    (19)

То есть существует ли конечное состояние, такое, что b1 находится в R – этом конечном состоянии.

Решение состоит в реализации перехода:

Sk1 = сдвиг( И, b1, h1, R, SH).       (20)

Полученное решение характеризует одношаговый процесс, который протекает вполне очевидным образом, путем использования аксиом α ₁ и α ₂.

Теперь рассмотрим вторую задачу, которая формулируется аналогично первой:

( ∃ S_k2) { находится ( b₂, R, S_k2) }.     (21)

Совершенно аналогично можно показать, решением задачи будет:

Sk2 = сдвиг( И, b2, h2, R, SH).        (22)

Тогда исходная задача, сформулированная выше, в терминах исчисления последовательности операторов преобразования будет иметь следующий вид:

(Sk3) { находится ( b1, R, Sk3)

находится ( b2, R, Sk3) }?      (23)

Решение этой задачи, полученное из аксиом α ₁, α ₂ и α ₃:

S_k3 = сдвиг( И, b₁, r₁, r, сдвиг( И, b₂, r₂, r, S_H)) (24) или сдвиг( И, b₂, r₂, r, сдвиг( И, b₁, r₁, r, S_H)). Такой результат показывает, что проект реализует положительного. Однако в плане требований однозначности решения третья задача неразрешима при данных аксиомах α ₁, α ₂ и α ₃, но существует множество различных путей выполнения аксиом α ₁, α ₂, α ₃, позволяющих обеспечить единственность решения. Введем аксиому α ₄, которая делает нашу задачу разрешимой в плане единственности решения:

α ₄: ( ∀ х, у, s, r₁, r₂, r) { находится ( х₁, r₁, s)

⇒ находится ( х₁, r₁, сдвиг (И, у, r₂, r₁, s)) }. (25) Предлагаемая аксиома фиксирует тот факт, что положение некоторого объекта А, не тождественного у, не меняется при перемещении у. Если имеются два объекта, один из которых обрабатывается х находится в r₁, а другой – у - в r₂, то перемещается объект из r₁; другой остается без обработки и он не движется. Аксиома α ₄ утверждает, что за один переход обрабатывается и перемещается только один объект. Поясним, почему не получалось решение в исходной постановке задачи.

В начальном положении два элемента b ₁ и b₂, находятся соответственно в точках r₁ и r₂. При переходе из S_H в S₂ сдвигается первый элемент, а в конечном состоянии сдвинуты оба элемента. Но не существует гарантии, что в промежуточном состоянии S_k сохраняла силу аксиома α ₂ и поэтому задача была неразрешимой, т.е. путь перехода из начального состояния S_H в конечное S_k не был единственным.

Задача исполнителя заключается в том, чтобы выполнить соединение. Сформулируем задачу согласно методики исчисления последовательности операторов преобразования в соответствии с предикатами:

Предикаты Р : находится на (x, y, s);

находится у (x, y, s) ;    (26)

находится в (x, y, s) ;

Перемещение (И, х, r1, r2, s) – ориентирование, F = (И, х, r1, r2, s), совмещение (И, х, r1, r2, s),(27)

А = {И, k, Р, G, θ , r₁}.         (28)

Здесь первый предикат означает, что х находится на у в состоянии S. Далее использованы обозначения: И – для исполнителя, k – для стенки нервюры, Р – для стойки, G – обозначает место установки стойки, θ – инструмент, начальное положение которого обозначим через r₁.

Зададим систему аксиом. Аксиома α ₁ описывает начальное условие, а именно, что инструмент и находится в r₁ в состоянии S_H.

Стойки, подлежащая монтажу, находятся на стеллаже исполнителя; который находится в состоянии SH. Аксиома представляет собой конъюнкцию трех предикатов:

α ₁: находится на ( θ , r₁, S_H) находится у (И, G, S_H ) находится на (Р, k, S_H).              (29)

Аксиома α ₂ выражает свойства некоторых элементов сохранять отношения при всех состояниях, при этом можно сказать, что стойки k и инструмент и всегда находятся на столе G:

α ₂ : ( ∀ S) { находится на ( k, F, S) находится на (и, G, S) }.                                 (30)

Аксиома α ₃ продолжает аксиому α ₁.

α3: (∀ S, х, r1, r2) { находится на ( х, r1, S) находится у (И, G, S) находится на ( х, G, S) ⇒ находится в (х, r2, перемещение (Э, х, r1, r2, S)).      (31)

Аксиома α ₄ и аксиома α ₅ завершают систему аксиом:

α ₄: ( ∀ S) { находится у (И, G, S) находится на ( θ , G, S) находится у ( и, k, S) ⇒ находится над

(И, k, ориентация (И, θ , G, k, S)) }.      (32)

α ₅: ( ∀ S, х, r₁, r₂) { находится на (x, k, S) находится у ( И, k, S) ⇒ находится над (x, G, совмещение (И, x, k, G, S)) }.   (33)

Поставим задачу следующим образом: существует ли конечное состояние Sk, в котором инструмент и совмещен со стойкой Р стенки нервюры k:

• ( ∃ S_k) находится на ( Р, и, S_k)? (34)

Решение:

Sk совмещение (И,Р, k, и ) ,ориентация

(И, и, G, k, Р) , перемещение (И, и, r1, k, SH).(35)

Следовательно, появляется план решения задачи. Исполняя эти три функции в обратном порядке, мы получаем способ совмещения инструмента и со стойкой Р стенки нервюры k следующему алгоритму: сначала инструмент и перемещается исполнителем к коробке, далее исполнитель ориентирует инструмент и относительно стойки Р, установленной на стене k, и, наконец, исполнитель совмещает инструмент и стойку в месте соединения, достигая конечного состояния Sk.

Эффективность решения логических задач в исчислении последовательности операторов преобразования достаточно высокая. Для того, чтобы эту эффективность сравнять с эффективностью выполнения операций при заданной точности, необходимо иметь управляющее устройство на самом высоком уровне, которое устанавливало бы правильное соответствие между планированием и исполнением операций. В дальнейшем этот вывод будет положен в основу создания искусственной системы управления процессами сборки узлов и агрегатов летательных аппаратов.

Тогда, прежде чем исполнять оператор, сначала проводится идентификация предиката Q, связанного с результатом действия F1. Если оператор F1 выполнен верно, исполняется оператор F2. Если получен отрицательный результат, действия по оператору F2, должны быть скорректированы и повторены и т.д. Практически значимым результатом прогноза правильных действий исполнителя должен быть алгоритм ,учитывающий влияние входов различной длины и содержания на качество процессов сборки. На рис .2 показана схема такого алгоритма.

ВЫВОДЫ

Получены вероятностно-динамические модели производственных систем, составляющие основу системы принятия решений в прикладных задачах разработки реальных проектов технологии агрегатной сборки , где число элементов собираемых узлов всегда конечно, но не определено однозначно по фактическому состоянию в динамике на множестве рабочих мест исполнителей. В соответствии с моделями представлений определяются оптимальные

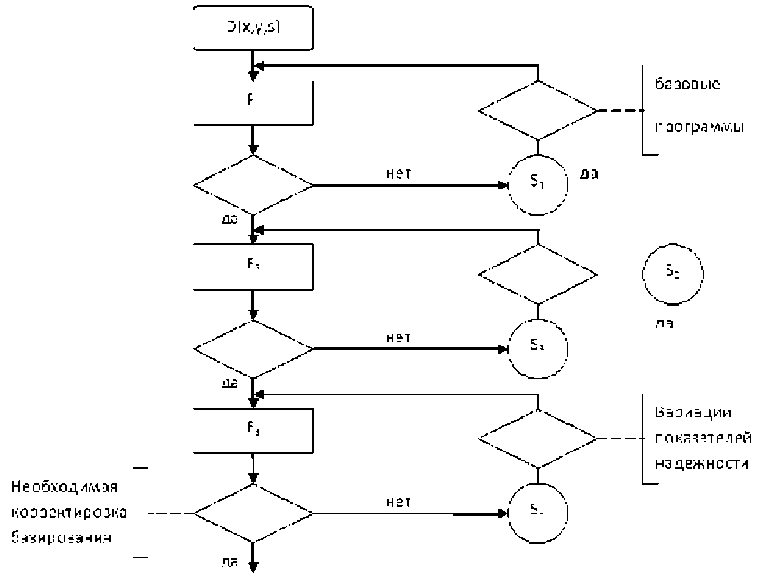
Рис. 2. Алгоритм реализации вероятностной модели процесса сборки на входах фиксированной длины как дискретной ограниченной случайной величины

мальные критерии образования новой ТС, которая изменяется вместе с пространством её представления. При развитии производственно-технологических систем все действия, нацеленные на структурообразование, приводят к проектному изменению состояний как результатов переходных процессов преобразования комплектующих, и могут быть описаны вероятностно-динамическими моделями. Системное структурообразование связывается с упорядоченной логикой деятельности исполнителей на множестве последовательностей рабочих мест. Его принципы обосновываются общей моделью сборочного пространства в виде графа как основой ТС.

• 3.

• 4.

• 5.