Теория непараметрических систем. K-модели

Проблема идентификации является одной из центральных в теории управления и других областях науки, объединяемых емким термином – кибернетика. Основное внимание мы уделим задачам идентификации в «широком» смысле, наряду с достаточно хорошо развитой теорией идентификации в «узком» смысле. Ранее [1–3] были описаны дискретнонепрерывные процессы и пути идентификации стохастических систем, которые тесно связаны с имеющейся априорной информацией.

Более того, нас будет интересовать прежде всего идентификация в условиях непараметрической неопределенности, а также случай, когда априорная информация соответствует одновременно как непараметрическому [3], так и параметрическому типу исходных данных об исследуемом процессе. Приведем достаточно общепринятую схему задачи идентификации (рис. 1) [4].

На рисунке приняты следующие обозначения: u_t , x_t – соответственно векторные входные и выходные переменные, контролируемые в дискретные моменты времени t; ^ t - случайная ненаблюдаемая помеха;

Теория – в виду практики.

Девиз конгрессов IFAС

При изучении неизвестных явлений можно строить очень общие гипотезы и продвигаться шаг за шагом с помощью опыта. Слишком конкретная гипотеза почти наверняка заключает в себе долю ошибки наряду с долей истины

П. Кюри xˆt – выходная величина настраиваемой модели; st = xt - xt; Q (st) - выпуклая функция потерь; a -вектор параметров настраиваемой модели; It – вектор всех наблюдений к моменту времени t ; M – символ математического ожидания; R (a) - критерий идентификации.

Идентификация по данной схеме осуществляется при помощи настраиваемой модели (блок «модель») той или иной параметрической структуры, параметры a которой корректируются по мере поступления наблюдений «вход-выход». Обычно предполагается, что объект работает в стационарном режиме, т. е. вероятностные характеристики последовательностей xs, йs неизменны во времени,     xs =( x1, x 2,..., xs), йs =(u1,u2,..., us) - временные векторы. Соответствие настраиваемой модели объекту оценивается критерием качества идентификации:

R (a) = M {Q (s( xt, xt))}.            (1)

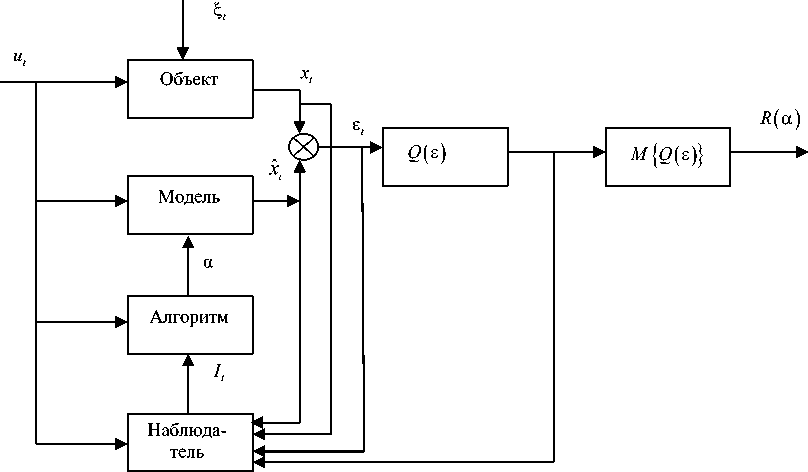
Рис. 1. Схема задачи идентификации

Алгоритм идентификации (блок «алгоритм») определяется параметрической структурой модели, видом функции потерь, методом минимизации критерия качества идентификации R ( а ) по а , т. е. нахождением такого а * , что

R ( а * ) = min R ( а ) . (2)

Решение задачи (2) может быть получено, например, методом стохастических аппроксимаций, методом наименьших квадратов, методом случайного поиска и др.

Постановка задачи. Рассмотрим более общую схему дискретно-непрерывного объекта (рис. 2). Здесь приняты обозначения: х ( t ) - векторная выходная переменная процесса; и ( t ) - векторное управляющее воздействие; ц ( t ) - векторная входная переменная процесса; £ ( t ) - векторное случайное воздействие; ( t ) - непрерывное время; H ^ц , H u , H^х , H ^to - каналы связи, соответствующие различным переменным, включающие в себя средства контроля, приборы для измерения наблюдаемых переменных; ц _t , u_t , x_t , to _t -означает измерение ц ( t ), и ( t ), x ( t ), to ( t ) в дискретное время t ; to i ( t ): i = 1,2,..., k - переменные процесса, контролируемые, в том числе, по длине объекта.

Отметим существенное отличие выходных переменных z ( t ), q ( t ) и x ( t ), представленных на рис. 2. Выходная переменная x ( t ), как и ц ( t ), и ( t ), контролируется через интервалы времени A t , q ( t ) контролируется через существенно большие интервалы времени A T , z ( t ) - через T ( T >>A T >>A t ).

С практической точки зрения для исследуемого процесса наиболее важным часто является контроль переменных z ( t ). Например, выходные переменные x ( t ) контролируются с помощью различного рода индукционных, емкостных и других датчиков, доступных электрическому измерению, q ( t ) - на основе лабораторных анализов, а z ( t ) - в результате длительного химического анализа, физико-механических испытаний и др. Этим и обусловлено существенное различие дискретности контроля выходных переменных q ( t ) и z ( t ). Особенностью здесь является то, что измеренное значение выхода объекта станет известным только через определенные промежутки времени, этим объясняется запаздывание в измерениях выходных переменных объекта x ( t ), q ( t ) и z ( t ), а A t , A T и T - дискретность, с которой происходят измерения.

В этом случае выходные переменные, как и ранее, зависят от входных и ( t ), ц ( t ), £ ( t ), а to ( t ) играет роль дополнительной информации, и тогда процесс описывается следующим образом:

х ( t ) = А ( u ( t ), ц ( t ), ^ ( t ), t ). (4)

Достаточно подробный анализ такого процесса был проведен в [1; 2]. Конкретные задачи идентификации будут ниже приведены с указанием различий в каждом рассматриваемом случае. Из рис. 2 ясно, что значения выходных переменных x ( t ) , q ( t ) , z ( t ) объекта зависят от входных u ( t ) , ц ( t ) , £ ( t ) . Полученные to ( t ) представляют дополнительную информацию о протекании исследуемого процесса, которую целесообразно использовать при построении модели.

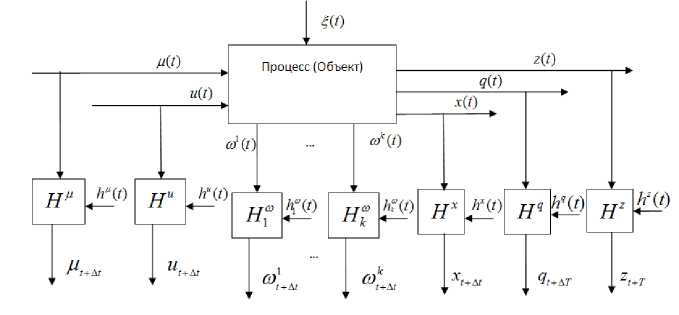
Рис. 2. Общая схема многомерного стохастического процесса

Таким образом, основная задача идентификации состоит в построении моделей, которые в достаточно общем виде могут быть представлены следующим образом:

x ( t ) = A ( u ( t -т ) , р ( t -т ) , ю ( t -т ) ) ,          (5)

• < ( t ) = A ( u ( t -т ) , р ( t -т ) , ю ( t -т ) , x ( t ) ) ,       (6)

z ( t ) = A ( u ( t -т ) , р ( t -т ) , ю ( t -т ) , x ( t ) , <  ( t ) ) , (7) где т - запаздывание, отличающееся по различным каналам (из соображений простоты принято единообразное обозначение).

Многообразие задач идентификации будет обусловлено различными объемами априорной информации, типами процессов, наличием запаздывания в объекте и каналах связи.

H-модели безынерционных объектов. Сделаем следующие допущения: объект, представленный на рис. 2, - безынерционный, переменные ю(t) = («'(t),...,гоk (t)), <(t), z(t) отсутствуют вместе со своими каналами измерения. В этом случае объект описывается зависимостью х (t) = А (u (t), р( t), ^( t), t).              (8)

Примем, что модель такого объекта с запаздыванием имеет вид

x ( t ) = А ( u ( t - т ), р ( t - т ), а ),          (9)

где A - выбранный класс функций; а - вектор параметров; т - запаздывание.

Запаздывания по различным каналам связи, конечно же, могут быть различными, но мы не будем это отмечать в формулах, чтобы не перегружать их индексами. Отметим лишь, что все запаздывания по соответствующим каналам связи известны.

Рассмотрим еще один процесс, часто имеющий место на практике [2]. Сущность его состоит в том, что из-за стохастической зависимости компонент вектора входных переменных, которая почти всегда неизвестна, исследуемый процесс имеет «трубчатую»

структуру. Пусть u е R ¹, ре R ¹, x е R ¹ (рис. 3). Интервалы изменения ( u , р , x ) е R ³ всегда известны из практических соображений. Без нарушения общности выделим в R ³ единичный куб. Реально протекающий процесс же принадлежит подобласти Q H ( u , р , x ) с Q ( u , р , x ), которая никогда не известна.

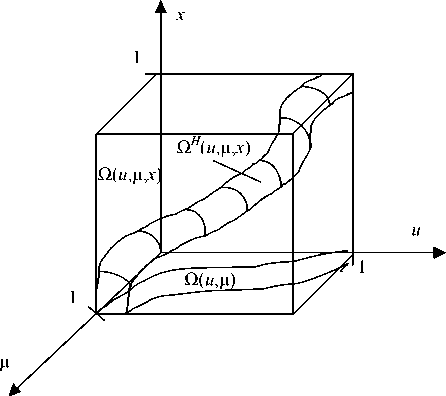
Рис. 3. Процесс, протекающий в трубке

Таким образом, u е[0;1], ре[0;1], x е[0;1], а триада (u, р, x) eQ(u, р, x). Ясно, что не каждое значение триады (u, р, x), полученной в эксперименте или измеренной на реальном процессе, будет принадлежать QH (u, р, x). Следует отметить, что в теории идентификации области Q(u, р, x), Q(u, р), Q(u), Q(р), Q(x) всегда известны, а область QH (u, р, x) всегда неизвестна. В случае стохастической независимости входных переменных процесса QH (u, р, x) совпадает с Q(u, р, x), т. е. QH (u, р, x) = Q(u, р, x). Если объект динамический, то переменные фазового пространства обязательно стохастически зависимы. Это, безусловно, накладывает отпечаток и на особенности моделирования подобных процессов, которые мы рассмотрим в дальнейшем.

Параметрическая модель статического процесса (см. рис. 1) может быть принята в виде [3; 4]

x ( и , Ц ) = F ( и , Ц , а ),               (10)

где F(■) - некоторая функция; а - вектор парамет- ров, например,

N

x ( и , Ц ) = ^ а , -ф , -( и , ц ),              (11)

i = 1

где ф , , i = 1, N - система линейно-независимых функций; ( и , ц ) ей ( и , ц ) , ( и , ц , x ) ей ( и , ц , x ). В случае стохастической зависимости компонент векторов и е R n , ц е R m исследуемый процесс имеет «трубчатую» структуру [1]. Тогда параметрическая модель должна быть взята в виде

Х ( и , Ц ) = F ( и , Ц , а ) I ( и , ц ) ,        (12)

векторов и = ( и , ,..., и п ) , ц = ( ц , ,..., ц _т ) , x = ( x , ,..., x_e ) , 1

• т. е. и'' , например, отличен по составу от компонент 2)

вектора и' '. В частности, может иметь место следующее: и=(и1,и3,и4,и7), а и42* =(и2,и3,и5,и8,и9). То же самое относится к векторам цей(ц)с Rm, к x е Q(x) с Rl и к последующим аналогичным обо- значениям.

Пусть исследуемые процессы имеют «трубчатую» структуру, тогда модель (14) имеет вид x,(и (t), ц( t )) =

= F -( и ( t -т ) , ц ( t -т ) ) I s ( и ( t -т ) , ц ( t -т ) ) ,

где индикатор Is (■) (в дальнейшем, при наличии ин декса s, мы будем опускать в формулах временные векторы)

I s ( ^и ( t ^-т) , Ц ( t ^-т) ) =

= Is (и(t-т),ц(t-т),иs,Цs), где I(и, ц) - индикатор такой, что

I ( и , ц ) = •

1, if ( и , ц ) ей H ( и , ц ) сй ( и , ц ),

такой,что

I s ( ^и ( t ^-т) , Ц ( t ^-т) ) =

if ( и , ц ) gQ H ( и , ц ).

1, У ( и ( t -т ) , ц ( t -т ) ) ей H ( и , ц ) , (18) 0, ,f ( и ( t -т ) , ц ( t -т ) ) йй H ( и , ц ) .

Ясно, что, если Q H ( и , ц ) = Q ( и , ц ), то модель (12) совпадает с обычными моделями (10) либо (11). В качестве оценки индикаторной функции I ( и , ц ) может быть принята статистика:

Модель процесса (15) будет выглядеть следующим образом:

к ^{1 if}

I S ^{( и} , Ц ) = <

0, if

sn

Шф

и,- - и

cs

m

'ц ,

-

Ц

I c s J

> 0,

sn

ЕП ф

и , - и

c

m

П Ф

'ц

-

Ц

I c s J

< 0.

Здесь колоколообразные функции Ф ( ^ ) и параметр размытости c_s удовлетворяют условиям сходимости [3], и е R n , ц е R m , x е Q ( x ) с R^e .

KH-модели безынерционных объектов. Здесь примем те же предположения, что и ранее, тогда x,(и(t),ц(t)) = F(и(t-т),ц(t-т)), 1 = 1,l (14) или в более общем виде fi (и1\ t-т), цМ( t-т), x \ t )) = 0, 1 = 1, l. (15)

Здесь F ( ■ ) и f ( ■ ) - неизвестные функции, соответствующие тому или иному классу, индекс (^ указывает, что векторы и , ц , x в данном случае составные. Это значит, что и* \ Ц ¹\ x-, , 1 = 1, l составлены из различных наборов компонент соответствующих

f ( и¹' ^} ( t - т ) , ц^ ( t - т ) , x⁽ ‘ ( t ) ) х х I s ( и'^! ( t -т ) , ц^ ( t -т ) ) = 0, , = 1, l ,

где индикатор I ' ( ■ ) равен

Is ( ^и< ‘ ( t ^{- т}) , o^W ( t ^{- т}) , ^и^ , ^Ц° ) =

' 1, if ( и , ц ) ей H ( и , ц ) ,            (20)

0, if ( и , ц ) ей H ( и , ц ) .

Модели класса (16)-(20) будем называть КН-моде-лями безынерционных объектов с запаздыванием, поскольку они принципиально отличаются от общепринятых моделей [4; 5] не только потому, что описывают процессы «трубчатой» структуры, но и наличием априорной информации по различным каналам многомерного объекта как параметрического, так и непараметрического типа. Более конкретно модель подобного объекта может быть представлена следующим образом:

f ( и^t -т ) , o^W( t -т ) , x-¹ ^( t ) , а ) I s = 0, , = 1, k ,

< S , ( ^{и }}( t ^-т) , ^{Ц 1 >}( t ^-т) , x >( t ) , й ^\ ^Ц s\ x s^ ^а ) I s = 0, ⁽²¹⁾

1 = k + 1, l ,

где а - вектор параметров; I Si , i = 1, k - индикатор (20); S i , i = X + 1, 1 - соответствующие непараметрические статистики; f ( ■ ) , i = 1, X - семейство параметрических функций, определенных на основании априорной информации [3].

Система уравнений (21) представляет собой модель многомерного многосвязного безынерционного объекта с запаздыванием, который относятся к классу КН-моделей, принципиально отличающихся от известных [4; 5]. Их отличие состоит в том, что по отдельным каналам многомерного процесса известна его параметрическая структура с точностью до параметров а . Она может быть определена на основе фундаментальных законов физики, механики, электротехники и др.

Вторая группа уравнений (21) S i , i = X + 1, 1 1 соответствует уровню непараметрической неопределенности. В этом случае мы можем располагать априорной информацией лишь качественного характера об исследуемом объекте и используем стохастические аппроксимации непараметрического типа.

Оценка параметров а в X -уравнениях (21) может быть сведена к задаче идентификации в «узком смысле». Оценка второй группы уравнений S i , i = X + 1, 1 в (21) может быть осуществлена непараметрическими методами [3]. Если система уравнений (21) распадается, т. е. в случае процесса, описываемого (14), то по известным значениям u ( t ) и ц ( t ) можно легко дать прогноз x ( t + т ) , если же нет, тогда возникает необходимость решения системы (иначе, КН-модели) относительно вектора x eQ ( x ) с R^e . В случае наличия одного корня системы (21) в Q ( x ) возможно использовать прием, изложенный в [3]. Вообще говоря, этот вопрос требует специального исследования.

K-модели динамических объектов. Рассмотрим задачу построения модели динамического процесса (см. рис. 2). Отметим, что A T и T значительно превышают постоянную времени объекта по всем остальным каналам.

Без нарушения общности можно считать, что контроль переменных u ( t ) , ц ( t ) , ю ( t ) , x ( t ) осуществляется через интервал времени A t << A T <<  T . Следовательно, процесс по каналам q ( t ) и z ( t ) относит -ся к классу безынерционных с запаздыванием, а по каналам ю ( t ) и x ( t ) может быть отнесен к классу динамических, так как их контроль осуществляется через интервал A t значительно меньший, чем постоянная времени объекта по соответствующим каналам. В этом случае достаточно общая K-модель может быть принята в виде

f I uW (t - т), p^‘^ (t - t) , юi> (t - t) , x' (t V

d ² x i ( t )

dt ²

)

., а = 0, i = 1, k ;

< f ( U i ( t - t ) , ^ ^{i >} ( t - t ) , ю ^{i >} ( t - t ) , x ^W ( t ) ,

q4t ) , z^^t ) , p ) IS = 0, i = k + 1, 1 1 ;

Si (u W (t - t) , pW (t - t) , ю‘^ (t - t) , xi (t), q«(t),z^(t),US ) 0, i = 1 +1,12, 12 > 11 > 1, где первая группа уравнений (22) найдена на основе известных фундаментальных законов, соответствующих исследуемому процессу с точностью до параметров а. Вторая группа уравнений объекта получена на основе имеющейся априорной информации с точностью до вектора параметров р. Третья группа уравнений (22) не известна с точностью до параметров, но класс функций, характеризующих взаимосвязь «вход-ных-выходных» и промежуточных переменных, определен на основе априорной информации. Фигурирующее в ней обозначение Wsi представляет собой совокупность всех i-х наблюдений переменных объемом s , т. е.

-------* -------* --------* -------* -------* -------* \

u Si , p S °, ю S °, x si , q Si , z^ ) , ‘ = ¹ 1 + 1, ¹ 2.

Оценка значений компонент векторов выходных переменных x ( t ) , q ( t ) , z ( t ) может быть найдена в результате решения системы уравнений (22) при фиксированных значениях u ( t ) , p ( t ) , ю ( t ) . K-модели принципиально отличаются от общепринятых прежде всего тем, что учитывают во взаимосвязи все имеющиеся переменные и связи между ними в ситуации, когда дискретность контроля последних существенно различаются. Отличаются также и уровни априорной информации о различных каналах исследуемого процесса. Таким образом, K-модели представляют собой органический синтез, описывающий исследуемый процесс или систему взаимосвязанных объектов во всем их многообразии.

Основное содержание вышесказанного состоит в следующем. Во-первых, постановка задачи идентификации чаще всего должна осуществляться в условиях, когда частично мы находимся в условиях и параметрической, и непараметрической неопределенности. Это соответствует одновременно идентификации в «узком» и «широком» смыслах. Именно практика диктует нам требования, когда необходимо строить К-модели, – такова реальность. Во-вторых, при формулировке задачи идентификации необходимо обязательно учитывать имеющиеся средства контроля, дискретность измерения переменных, характеризующих состояние исследуемого процесса, случайные ошибки, непредставительность выборок, действие случайных возмущений и т. д. И, наконец, в-третьих, чаще всего мы лишены на практике возможности проводить желаемые эксперименты, потому что объекты «включены» в реально функционирующий производственный процесс. Необходимо с большой осторожностью на этапе математической постановки задачи произносить ставшие обычными допущения: «Пусть объект описывается…», «Имеем генеральную совокупность» и т. п. Только учет всех перечисленных выше факторов позволяет строить качественные модели реальных дискретно-непрерывных процессов и использовать их в дальнейшем для целей управления.