Теория непараметрических систем. Общий подход

Теория - в виду практики.

Девиз конгрессов IFAC

Теория автоматического управления предполагает выбор (определение) уравнения объекта с точностью до набора параметров. При этом существенное значение имеет априорная информация об исследуемом процессе. В фундаментальных монографиях А. А. Фельдбаума [1] и Я.З. Цыпкина [2] рассматриваются различные уровни априорной информации об исследуемом процессе при решении задач идентификации и управления. Методы классической и современной теории автоматического управления подробно рассмотрены в [3-7]. Основы применения теории случайных функций к задачам автоматического управления заложены в [8].

Уровни априорной информации. Под математической моделью объекта (процесса) обычно понимают его количественную формализацию. Математическая модель -это формальное описание процесса с помощью математических средств: дифференциальных, интегральных, интегро-дифференциальных, разностных, алгебраических уравнений, а также неравенств, множеств и т. д. [3]. Крайне важным является ответ на вопрос: как выбрать оператор объекта, превращающий входные переменные, дей-

Опыт - единственный источник истины.

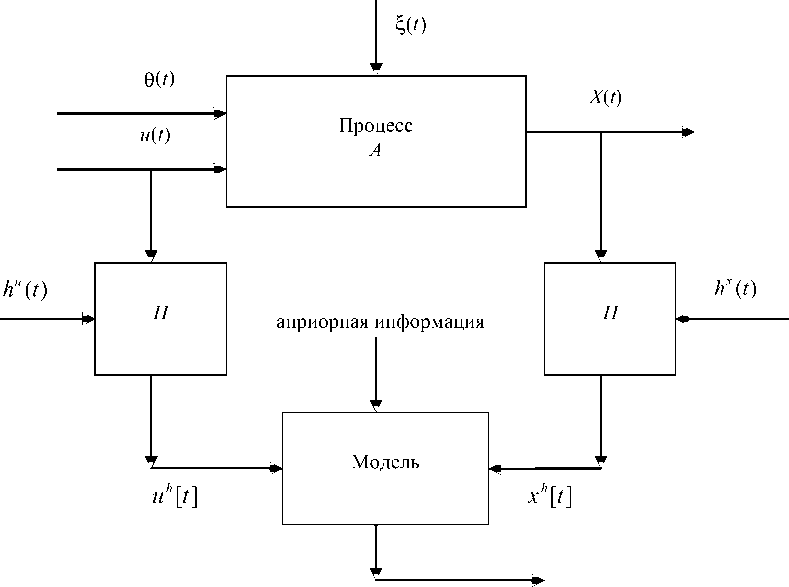
А. Пуанкаре ствующие на него, в выходные. В некоторых случаях возможно использование фундаментальных законов, лежащих в основе функционирования физических, химических, биологических и других процессов, т. е. имеющих место для механических, электрических, электромагнитных, термодинамических, гидравлических, электрохимических, биофизических и других процессов. К сожалению, мы часто сталкиваемся с серьезными трудностями на этом пути, особенно при изучении технологических, социальных, экономических и многих других процессов, т. е. сталкиваемся с неполнотой информации об интересующем нас процессе. И степень нашего незнания может быть существенно различной. В этой связи Л. Бриллюэном было отмечено, что «всякая плодотворная гипотеза кладет начало удивительному извержению потока непредвиденных открытий», но с другой стороны «физические модели отличаются от мира так же, как географическая карта от поверхности Земли». Имеющийся опыт теории и практики решения задач идентификации убеждает, что априорная информация и ее использование при моделировании исследуемого процесса может оказать- ся определяющей. Достаточно в общем виде это может быть представлено схемой (см. рисунок)

В блоке «Модель» определен принятый класс моделей на основании априорной информации об исследуемом процессе и анализе текущей информации {uh [t], xh [t], t = 1,5}, здесь же осуществляется настройка (обучение) модели принятого класса. В дальнейшем обучающую выборку {uh[t],xh[t],t = 1,5} ,из соображений простоты записи, будем обозначать {u[t], x[t], t = 1,5}.

Итак, математическое представление исследуемого процесса может быть представлено в виде: x (t) = A(u (t), 6( t), £( t), t), а его модель в форме:

x [ t + 1] = A (и [ t + 1],[ t ]),

где A - оператор модели, кроме того, все случайные факторы, действующие в каналах измерения и на процесс, имеют нулевые математические ожидания и ограниченные дисперсии.

Системы с полной информацией. В этом случае оператор процесса Ав(1) известен точно, а случайные помехи, действующие на объект и каналах связи отсутствуют, кроме того

u ( t ) е Q ( u ( t )) ,                   (3)

где Q(u (t)) - некоторая известная область допустимых значений u (t). При решении задач идентификации и управления могут быть использованы методы математической теории оптимальных процессов [9; 10], а также другие методы.

Системы с максимальной, но неполной информацией. Здесь предполагается, что помехи h ( t ) на рисунке отсутствуют, но помеха £ ( t ) может быть точно измерена, отсутствует также входная переменная 6 ( t ) , а операторА известен точно. Подробно этот случай исследовался в [1] для непрерывных, дискретно-непрерывных и чисто дискретных систем.

Системы с неполной информацией. Это системы с независимым (пассивным) накоплением информации [1]. В этом случае влияние входного воздействия 6 ( t ) воспринимается как просто случайное воздействие, аналогичное £ ( t ) , тогда мы имеем дело с объединенным входным случайным воздействием ( 6 ( t ), £ ( t )). Тем не менее, природа этих случайных воздействий на процесс существенно различна. Помехи £ ( t ) - это обычно предполагаемое в теории стохастических систем случайное воздействие на объект, 6 ( t ) - переменные, «имена» которых известны исследователю, но не подающиеся контролю, либо их контроль возможен частично через значительно (в десятки и сотни раз) превышающий A t . Кроме того, класс операторовА не известен точно, но необходимы предположения о плотности распределения всех слу-

x [ t ]

Схема использования априорной информации об исследуемом процессе: А - оператор процесса; Н- каналы измерения соответствующих переменных процесса; u(t) - Х-мерный вектор контролируемых входных переменных;

6 ( t ) - вектор входных переменных не поддающихся контролю; x(t) - «-мерный вектор выходных переменных; h^u ( t ), h^x ( t ) - случайные помехи при измерении соответствующих переменных; u^h [ t ], x h [ t ] - наблюдения переменных в дискретные моменты времени t через соответствующие интервалы времени A t ; ^ ( t ) -случайные помехи, действующие на процесс; x ( t ) -выход модели

чайных факторов (см. рисунок), уравнения каналов связи Л, и о классе оператора A с точностью до вектора параметров. Обычно плотности вероятности случайных факторов, действующих на объект и в каналах измерения переменных, предполагаются нормальными и аддитивными. Ясно, что в этом случае необходимо наличие выборки { и [ t ], x [ t ], t = 1, 5 } , а сами наблюдения предполагаются статистически независимыми [1], т. е. наблюдения, например и [1], и [2],... - независимы. Такие системы относят к классу разомкнутых или нейтральных.

Системы с активным накоплением информации. Особенность этого уровня априорной информации состоит в том, что задачи идентификации и задачи управления здесь могут быть объединены. Элементы выборки измерений поступают последовательно в обучающую модель и систему управления, т. е. ( и [1] x [1]),( и [2] x [2]),( и [3] x [3]),... . Таким образом, в случае объединения этих задач выработка входных воздействий носит двойственный характер -они должны быть одновременно и изучающими, и управляющими, т. е. носить дуальный характер. Теория дуального управления была создана А. А. Фельдбаумом и существенно развита в [1]. Однако, если помехи, действующие на процесс, аддитивны и в каналах измерения, то в целом система дуального управления может быть приведена к разомкнутой, т. е. темп накопления информации оказывается независимым от значений входных переменных. Такие системы называют приводимыми к разомкнутым или нейтральными [1]. Но существует класс не нейтральных систем, т. е. класс неприводимых. Например, если £ ( t ) мультипликативна по отношению к и ( t ) . Такой случай также исследован в [1].

Системы с параметрической неопределенностью. Параметрический уровень априорной информации предполагает наличие параметрической структуры модели и некоторых характеристик случайных помех, обычными из них являются нулевое математическое ожидание и ограниченная дисперсия. Для оценивания параметров используются чаще всего разнообразные итеративные вероятностные процедуры. При этих условиях также решается задача идентификации в узком смысле [3], как и во всех предыдущих случаях.

Системы с непараметрической неопределенностью. Непараметрический уровень априорной информации не предполагает наличие модели, но требует наличие некоторых сведений качественного характера о процессе, например, однозначность, либо неоднозначность его характеристик, линейность для динамических процессов либо характер его нелинейности. Для решения задач идентификации на этом уровне априорной информации (идентификация в широком смысле) применяются методы непараметрической статистики.

Системы с параметрической и непараметрической неопределенностью. Важными с точки зрения практики являются задачи идентификации многосвязных систем в условиях, когда объем исходной информации не соответствует ни одному из вышеописанных типов. Например, для отдельных характеристик многосвязного процесса на основании физико-химических закономерностей, энергетических, закона сохранения массы, балансовых соотношений могут быть выведены параметрические зако номерности, а для других нет. Таким образом, мы находимся в ситуации, когда задача идентификации формулируется в условиях и параметрической, и непараметрической априорной информации. Тогда и модели представляют собой взаимосвязанную систему параметрических и непараметрических соотношений.

Синтез непараметрических алгоритмов. Приведем фрагмент синтеза непараметрической модели. Сформируем критерий оптимальности:

R ( x ) = М и { M x { Q ( x , x )/ и } } ,          (4)

где Q ( • ) некоторая выпуклая функция.

Задача отыскания наилучшего x сводится к минимизации R(x) по , т. е. к поиску такого xопт, что R(x °пт) = minx R(x). Ясно, что вид x будет определяться видом функции Q (x, x). Так, если Q (x, x) = (x - x )2, то xопт = x(u) = M {x/и} .               (5)

Непараметрическая оценка х(м) будет xSj(. и ) = sksk

Z x j п ф ( С ;¹ ( и _v - и _v [ t ])) хп ф ( С ;¹ ( и _v - и _v [ t ])), (6) j =1 v=1                             / j = 1 v=1

j = ¹ n , где колоколообразные функции Ф ( ) , параметр размытости С₅ удовлетворяет условиям сходимости [11].

В случае идентификации линейных динамических процессов может быть использован иной путь, известный из теории линейных операторов [12; 13]. Остановимся только на общих чертах этого пути.

Пусть оператор исследуемого процесса (влияние переменных 0 ( t ) и £ ( t ) опустим)

x ( t ) = Au ( t )}                     (7)

линеен, тогда он может быть представлен в достаточно общем виде при ненулевых начальных условиях (из соображений простоты рассмотрим случай скалярных u(t) и x(t))

x ( t ) = и ( t ) G (0) + j q ( t - т ) и ( т ) d т            (8)

где G(t) и q(t) - соответственно переходная и весовая функции системы в направлении «вход-выход». При нулевых начальных условиях (8) будет x (t) = jq (t -т) и (т) d т.                (9)

Как известно, оператор обратный оператору (8) будет иметь вид и ( t ) = A ^-1 x ( t ) и далее (при нулевых начальных условиях)

и ( t ) = x ( t ) Л (0) + j Х ( t - т ) x ( т ) d т .         (10)

Заметим, что оператор, обратный (8), также является линейным и ограниченным, а оператор, обратный (9), является линейным, но неограниченным.

Центральная идея непараметрического моделирования и управления линейными динамическими системами состоит в следующем. Сначала снимают на реальном объекте переходные характеристики, подавая на вход объекта единичный сигнал и ( t ) = 1( t ) , т. е. получают выборку x [ t ] через интервал времени A t , t = 1, 5 , затем строят непараметрическую оценку G₅ ( t ) и оценку q₅ ( t ) , исходя из того, что q ( t ) = dG ( t )/ dt . В результате непараметрическая модель примет вид:

x_s ( t ) = u ( t ) G_s (0) + j q_s ( t — t) u (t) d т . (11) 0

Следующий принципиально новый этап предложен в такой последовательности. Поскольку на реальном объекте нельзя снимать переходную характеристику в направлении «выход-вход», то переходная характеристика в этом направлении снимается на модели (11), т.е. u ( t ) = 1( t ) через интервал времени A t , таким образом, получается реализация x [ t ], t = 1, s . Далее аналогичным образом строятся непараметрические оценки Л _s ( t ) и X_s ( t ) , и далее строится оценка (10)

u s ( t ) = x ( t ) Л _s (0) + j X ( t - t) x (t) d т . (12) 0

Таким образом, (12) является непараметрическим регулятором линейной динамической системы, для этого достаточно положить x ( t ) = x * ( t ) , x * ( t ) - заданное значение выхода системы.

Существенным в вышеизложенном является то, что получен регулятор в условиях, когда вид уравнения с точностью до параметров, описывающих его процесс, не известен, как это делается в классической теории управления. Достаточно сказать, что в фундаментальной монографии [13], посвященной теории линейных систем на основе линейных операторов, не приведено ни моделей, ни регуляторов, которые можно было бы использовать на практике. В последующих статьях, посвященных теории непараметрических систем, будут детально изложены модели, решающие правила, алгоритмы управления, оптимизации, принятие решений, способы их настройки и различные тактики накопления информации в условиях непараметрической неопределенности, а также результаты моделирования для различных задач обучения и адаптации. Основное назначение настоящей работы состоит в том, чтобы показать место непараметрической теории при решении разнообразных задач адаптации и обучения в условиях малой априорной информации. В дальнейшем будет обращено специальное внимание на организационные системы. И здесь важное место будет уделено некоторым вопросам моделирования как в игровых [14], так и в стохастических процессах [15], кроме того, будут рассматриваться некоторые результаты непараметрического оценивания линейных операторов [16].

Таким образом, приведены различные уровни априорной информации, соответствующие, по существу, различным разделам теории управления. Проведен анализ подходов при построении адаптивных и обучающихся систем различного назначения. Отмечено, что в условиях непараметрической неопределенности неприменимы известные методы построения соответствующих алгоритмов. Показан фрагмент синтеза непараметрических алгоритмов идентификации статических и линейных динамических объектов. При этом специально обращается внимание на способ получения алгоритмов управления на основе теории линейных операторов. Дальнейший цикл статей будет посвящен более детальному рассмотрению теории непараметрических систем.