Теория непараметрических систем. Процессы

При изучении различного рода реальных процессов и объектов исследователь сталкивается с неполной информацией о последних, которая может существенно отличаться от реальности в зависимости от их характера, свойств, средств контроля и т. п. Это накладывает свой отпечаток при моделировании тех или иных процессов, включающих в себя априорную информацию о них, математическую постановку задачи, подходы и методы построения моделей, оценку адекватности полученной модели реально протекающему процессу. В зависимости от особенностей исследуемого процесса развиты различные подходы к идентификации и управлению [2-4].

Приведем достаточно общую схему исследуемого процесса, принятую в теории моделирования и идентификации [5; 6].

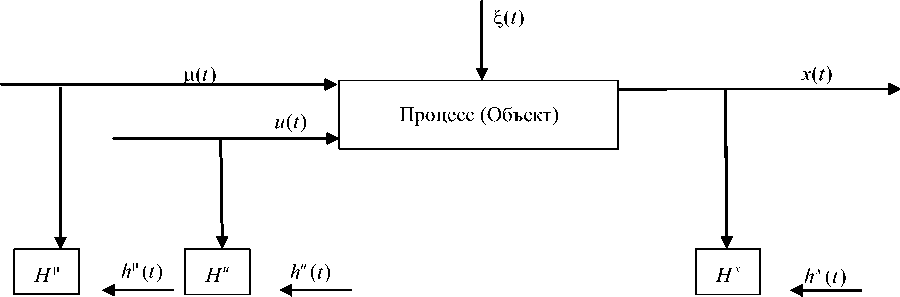
В рассматриваемой схеме (рис. 1) приняты следующие обозначения: х ( t ) - векторная выходная переменная процесса; и ( t ) - векторное управляющее воздействие; ц ( t ) - векторная входная переменная процесса;

£ ( t ) - векторное случайное воздействие; ( t ) - непрерывное время; H ^ц , H“ , H^х - каналы связи, соответствующие различным переменным, включающие в себя средства контроля, приборы для измерения наблюдаемых переменных; ц _t , u _t , x _t - означает измерение ц ( t ), и ( t ), x ( t ) в дискретное время. Контроль переменных ( x , и , ц ) осуществляется через интервал времени A t , т. е. x i , u i , ц i , i = 1, 5 - выборка измерений переменных процесса ( X , , и , , Ц 1 ) , ( x 2 , и 2 , ц 2 ) ,..., ( x_s , и , , ц 5 ) ,... ; ^{5 -}объем выборки; h ^ц ( t ), h^x ( t ), h^u ( t ) - со значком вверху -случайные помехи измерений соответствующих переменных процесса. В этом случае х ( t ) определяется следующим образом:

х ( t ) = А ( u ( t ), ц ( t ), ^ ( t ), t ),                  (1)

где А - неизвестный оператор объекта.

Заметим, что выход объекта х ( t ) зависит от всех входных переменных u ( t ), ц ( t ), £ ( t ).

Более общая схема дискретно-непрерывного процесса приведена на рис. 2.

ц t

ut

xt

Рис. 1. Классическая схема стохастического процесса и контроля переменных

Здесь приняты те же обозначения, что и на рис. 1: ю i ( t ): i = 1, 2,..., к - переменные процесса, контролируемые в том числе по длине объекта; H ^ю - каналы связи, соответствующие различным переменным, включающие в себя средства контроля, приборы для измерения наблюдаемых переменных; ю _t - измерение ю ( t ) в дискретное время, представляет собой дополнительную информацию о процессе. Контроль переменных ( х , ю , и , ц ) осуществляется через интервал времени A t , т. е. х, ю i ,..., ю к , u_i , ц i , i = 1, 5 - выборка измерений переменных процесса ( х ₁ , ю 1 , ..., w k , и , , ц 1 ) , ( х 2 , ю 2 ,..., ю ^к . , и 2 , Ц 2 ) , ■••> ( х , , ю , ,..., ю , , и , , ц , ),... ; ^{5 -}объем выборки; h ^ю ( t ) - случайные помехи измерений соответствующих переменных процесса. В этом случае х ( t ) определяется не только значениями входных переменных, как в (1), но и ю ( t ) и может быть представлена в следующем виде:

х ( t ) = А ( и ( t ), ц ( t ), ю ( t ), ^ ( t ), t ). (2)

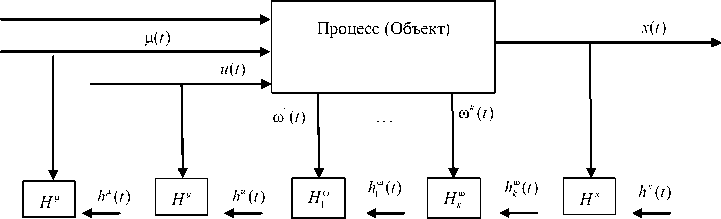
Следующий шаг обобщения исследуемого процесса (рис. 2) состоит во введении новой входной переменной Х ( t ) (рис. 3).

Входная переменная Х(t) существенно отличается по своему содержанию от переменных и(t), ц(t) и ю(t). Дело в том, что эта переменная не поддается измерению. Входная переменная Х(t) может быть известна исследователю, но ее контроль осуществляется достаточно редко и в соответствии, как правило, со сложной и длительной процедурой измерения. В этом случае х(t) определяется следующим образом:

х ( t ) = А ( и ( t ), ц ( t ), ю ( t ), Х ( t ), ^ ( t ), t ). (3)

Моделирование процессов подобного типа существенно усложняется в зависимости от характера влияния Х ( t ) на х ( t ).

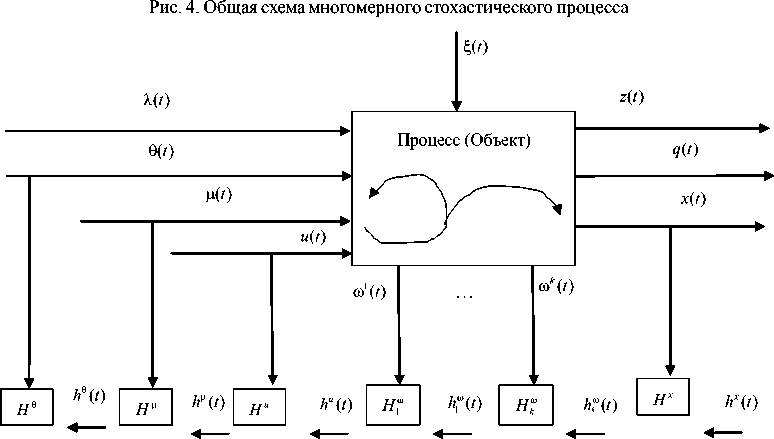
Приведем наиболее общую схему стохастического процесса, часто встречающегося во многих приложениях (рис. 4).

Отметим существенное отличие выходных переменных z ( t ), q ( t ) и х ( t ), представленных на рис. 4. Выходная переменная х ( t ) контролируется через интервалы времени A t , q ( t ) контролируются через существенно большие интервалы времени A T , z - через Т ( T >>A T >>A t ). С практической точки зрения для исследуемого процесса наиболее важным часто является контроль переменных z ( t ). Например, выходные переменные х ( t ) контролируются с помощью различного рода индукционных, емкостных и других датчиков, q ( t ) - на основе лабораторных анализов, а z ( t ) - в результате длительного химического анализа, физико-механических испытаний и др. Этим и обусловлено существенное отличие дискретности контроля выходных переменных х ( t ) и z ( t ). Особенностью здесь является то, что измеренное значение выхода объекта станет известным только через определенные промежутки времени, этим объясняется запаздывание в измерениях выходных переменных объек-

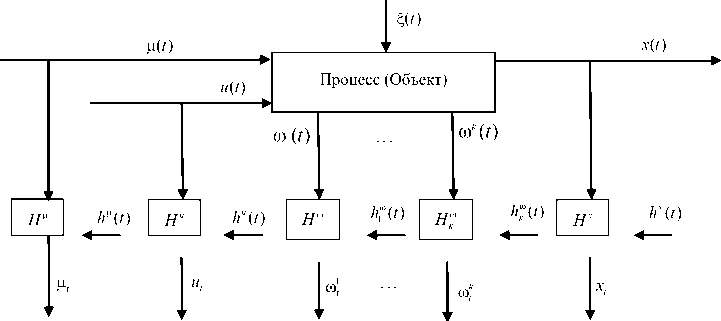
Рис. 2. Схема стохастического объекта, в том числе распределенного

К t )

Х ( t )

µ _t

ut

ю

^ω t ^k

xt

Рис. 3. Обобщенная схема стохастического процесса та x(t), q(t) и z(t). At, AT и Т- дискретность, с которой происходят измерения.

В этом случае выходные переменные, как и ранее, зависят от входных и ю ( t ) (дополнительная информация), т. е. следующим образом:

х ( t ) = А ( u ( t ), ц ( t ), ю ( t ), Х ( t ), ^ ( t ), t ).            (4)

При моделировании подобных процессов, учитывая различную дискретизацию контроля измерений x ( t ) , q ( t ) и z ( t ) при прогнозировании q ( t ) и z ( t ), естественно использовать весь набор переменных, влияющих на прогноз q ( t ):

q ( t ) = А ( u ( t ), ц ( t ), ю ( t ), X ( t ), x ( t ), ^ ( t ), t ),        (5)

а при прогнозе z ( t ):

z ( t ) = А ( u ( t ), ц ( t ), ю ( t ), X ( t ), x ( t ), q ( t ), ^ ( t ), t ).     (6)

Учитывая большие значения A Т и Т , значительно превышающих постоянные времени объекта, при моделировании придется учитывать, что процессы относятся к классу статических с запаздыванием, что значительно повышает их роль и значение в задачах идентификации стохастических систем.

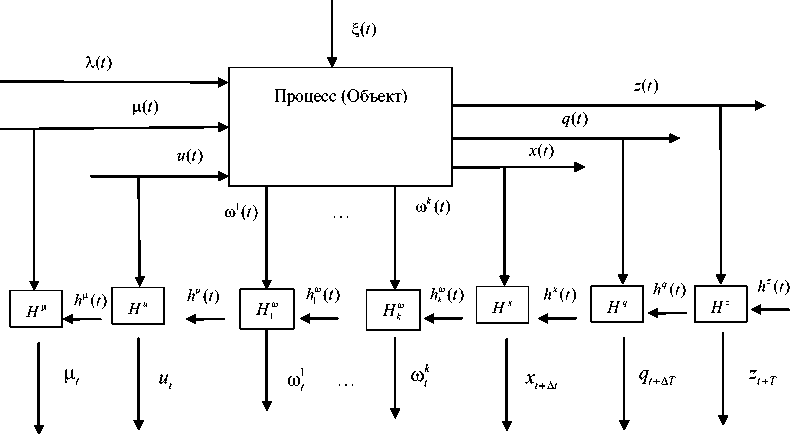
Организационный процесс можно представить в виде схемы (рис. 5) [6].

Заметим, что к организационным процессам относятся такие, которые протекают с участием человека (коллектива). Это символизируют стрелки, помещенные внутри объекта (рис. 5). Контроль переменных q ( t ) и z ( t ) осуществляется, как и x ( t ) (на рис. 5 не показан, чтобы не загромождать рисунок.) Переменная 0 ( t ) представляет собой воздействие на объект внешней среды. Для организационных систем это могут быть какие-либо рас-

θ t

xt

µ _t

ut

"■

ωtk

поряжения, постановления, приказы, а также законодательные акты, которые с течением времени претерпевают те или иные изменения.

В этом случае х ( t ) определяется следующим образом:

х ( t ) = А ( u ( t ), ц ( t ), ю ( t ), Х ( t ), 0 ( t ), ^ ( t ), t ). (7)

При прогнозировании q ( t ) целесообразно использовать следующие зависимости:

• q ( t ) = А ( u ( t ), ц ( t ), ю ( t ), Х ( t ), 0 ( t ), х ( t ), ^ ( t ), t ), (8) а при прогнозировании z ( t ):

• z ( t ) = А ( u ( t ), ц ( t ), ю ( t ), X ( t ), 0 ( t ), х ( t ), q ( t ), ^ ( t ), t ), (9)

Наконец, обратим внимание на важнейшее обстоятельство, возникающее при исследовании реальных процессов. Это средства контроля, измерения всех доступных переменных, характеризующих состояние процесса. Здесь следует отметить, что, если переменные процесса доступны измерению электрическими средствами, то это чаще всего позволяет установить желаемый интервал (дискретность) контроля. К таким переменным можно отнести все электрические переменные (ток, напряжение, частота и др.), а также влажность, температуру, давление, загрузку и др. Сложнее дело обстоит с существенными переменными, которые доступны контролю лабораторным способом (химический, физико-химический, физико-механический, петрографический анализ и др.). Дискретность контроля здесь может достигать часов, смены, суток и многих суток. Важнейшей здесь является сама процедура и технология отбора проб для дальнейшего анализа и измерения тех или иных переменных. На эти обстоятельства мы обратим специальное внимание в дальнейшем.

Отметим еще одну особенность, которая всегда имеет место на практике. Дело в том, что исследуемые процессы, протекающие в природных явлениях или в технических и технологических системах, почти всегда носят нестационарный характер. Иными словами, характер тех или иных зависимостей между переменными процесса изменяется с течением времени заранее неизвестным образом. Причины этого разнообразны и мы не будем их здесь рассматривать, укажем только одну, не вызыва ющую сомнения, - это старение оборудования или изменчивость среды, где протекает интересующий нас процесс. Заметим также, что во всех приведенных выше процессах отсутствует запаздывание, хотя предполагается, что оно имеет место. Это сделано из соображений простоты. Все это существенно влияет на исследование интересующего нас процесса, и часто является просто определяющим.

Приведем схемы двух основных структур, часто встречающихся в промышленности, экономике, социологии и др. Прежде всего, это последовательная схема (рис. 6), где объекты относятся к классу вышеприведенных (рис. 1-5), N - число объектов. Переменные из соображений простоты на рис. 6 не показаны.

Более сложной, но часто имеющей место на практике, является последовательно-параллельная схема, представленная на рис. 7.

Многообразие задач идентификации обусловлено характером и свойствами процесса, например: статический, динамический или распределенный; линейный или нелинейный (известен ли тип или класс нелинейности); с запаздыванием или без запаздывания; стационарный или нестационарный; случайные возмущения £ ( t ) аддитивные или мультипликативные, закон распределения £ ( t ) известен или нет; случайные помехи в каналах связи h ( t ) - аддитивные или мультипликативные, плотности вероятности их известны с точностью до параметров или неизвестны, сведения о моментах случайных величин, наблюдения переменных x_t , ю _t , u_t , ц _t статистически зависимы или нет и т. п.

Рассмотрим еще один процесс, часто имеющий место на практике [8]. Сущность его состоит в том, что из-за стохастической зависимости компонент вектора входных переменных, которая почти всегда неизвестна, исследуемый процесс имеет «трубчатую» структуру. Пусть u е R 1 , це R 1 , x е R ¹ (рис. 8). Интервалы изменения ( u , ц , x ) е R ³ всегда известны из практических соображений. Без нарушения общности выделим в R ³ единичный куб. Реально протекающий процесс же принадлежит подобласти О H ( u , ц , x ) с О ( u , ц , x ), которая никогда неизвестна.

Рис. 6. Последовательная схема процесса

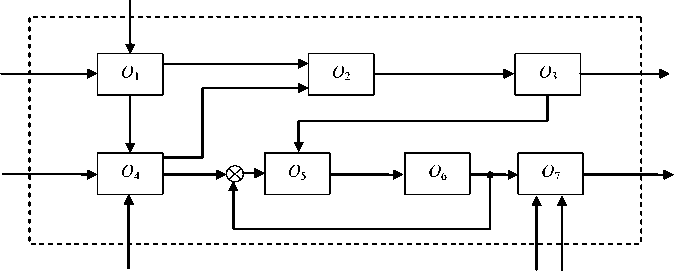
Рис. 7. Последовательно-параллельная схема процесса

Таким образом, и е [ 0;1 ] , це [ 0;1 ] , x е [ 0;1 ] , а триада ( и , ц , x ) е Q H ( и , ц , x ). Ясно, что не каждое значение триады ( и , ц , x ), полученной в эксперименте или измеренной на реальном процессе, будет принадлежать единичному кубу Q ( и , ц , x ). Следует отметить, что в теории идентификации области Q ( и , ц , x ), Q ( и , ц ), Q ( и ), Q ( p ), Q ( x ) всегда известны, а область Q H ( и , ц , x ) неизвестна никогда. Из соображений простоты иллюстрации мы рассматриваем статический объект. В случае стохастической независимости входных переменных процесса Q H ( и , ц , x ) совпадает с Q ( и , ц , x ), т. е. Q H ( и , ц , x ) = Q ( и , ц , x ) . Если объект динамический, то переменные фазового пространства обязательно стохастически зависимы. Это, безусловно, накладывает отпечаток и на особенности моделирования подобных процессов, которые мы рассмотрим в дальнейшем.

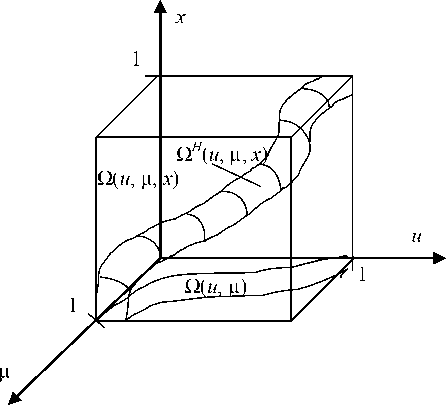
Рис. 8. Процесс, протекающий в трубке

Ниже рассмотрим процессы, часто встречающиеся на практике и являющиеся предметом исследования в теории распознавания образов. Типичным для задач технической диагностики, медицинской диагностики, диагностики состояния технологического процесса или объекта является наличие облачной структуры в пространстве признаков, определяющей тот или иной класс. Пусть некоторая ситуация (образ, процесс) может быть отнесена к тому или иному классу. Эта ситуация S характеризуется значениями вектора признаков v = ( v 1, ..., v_m ) и может быть отнесена к одному из двух классов V ₁ или V 2 . Задача распознавания образов сводится к построению решающего правила на основе имеющейся обучающей выборки { v s = ( v 1 ,..., v s ), U s }, где U s - указания учителя о принадлежности S к V 1 или V 2 ; s - объем выборки. Данная задача иллюстрируется для трехмерного вектора v , m = 3 (рис. 9). Элементы обучающей выборки { v s , U s } на рисунке не показаны из соображений простоты. В дальнейшем выборку наблюде ний переменных { v s = ( v 1 ,..., v s ), U s } объемом s будем обозначать { v s = ( v ₁,..., v s ), U s }, как это принято в монографии А. А. Фельдбаума [2]. Здесь же введен новый пограничный класс V ₃, который определяет область достаточно сильного перемешивания представителей обоих классов.

Таким образом, задачу обучения распознаванию образов из соображений практики целесообразно свести к трехальтернативной задаче распознавания.

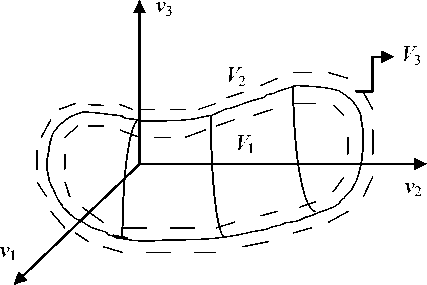
Рис. 9. Иллюстрация задачи распознавания образов

Рассмотрим класс процессов, относящийся к временным рядам. Временным рядом обычно называют наблюдения над некоторым процессом, явлением, порождающие упорядоченную последовательность, развернутую во времени t. Существенную роль при изучении временных рядов играет дискретность измерения At интересующей нас переменной x(t). Так можно говорить об урожайности сельскохозяйственных культур, выпадении осадков, численности населения и т. д. Отсюда видно, что дискретность измерения x(t) может быть год, месяц, день, а в некоторых технических процессах значительно меньше. Часто временной ряд представляют в виде xt = и, + h, t е T = (ti, t2,..., ts), (8) где и, - медленная составляющая исследуемого процесса (тренд), которая может порождаться некоторым закономерным образом, часто неизвестным исследователю; ht - случайная составляющая (помехи), независимая от и,. В фундаментальной монографии М. Дж. Кендалла и А. Стьюарта [9] выделены четыре основные составляющие временного ряда: тренд или систематическая составляющая; колебания относительно тренда с большей или меньшей регулярностью; эффект сезонности; случайная, несистематическая или нерегулярная компонента.

Вернемся к (8). Здесь существенную роль играет восстановление тренда Uz , но еще более важной является задача прогнозирования, предсказания xt, где t > ts. В настоящее время актуальными стали задачи прогнозирования необходимого количества продукции на следующий день, курса валют, продаж тех или иных изделий за различные интервалы времени и др. Анализ таких процессов показывает, что здесь недостаточно исследовать процесс типа (8). Совершенно необходимым является привлечение других факторов и переменных, существенно влияющих на xt, таким образом, (8) преобразуется к виду x, = ut(y) + ht, t е T = (ti, t2,..., ts), (9) где вектор y = (y1,..., yk) состоит из компонент, влияющих на поведение xt . Следует заметить, что компоненты векторау не обязательно вещественные, а могут принадлежать другим шкалам измерения.

Таким образом, в настоящей статье описаны процессы, часто встречающиеся в технологии, производстве, экономике, социологии и др., которые, за исключением, процесса, представленного на рис. 1, можно считать слабо изученными. Тем не менее, они представляются значимыми в связи с тем, что имеют прямое отношение к реальности. При моделировании этих процессов важнейшими являются уровень и объем априорной информации (основа для математической формулировки задачи идентификации), дополнительной информации об исследуемом процессе и средства и технология контроля, измерения переменных. Последнее особенно касается организационных процессов.