Теория представления математических моделей и последовательностей выполнения технологических операторов сборки самолетов

ях. Процесс кинематики выдается наблюдателю в виде компьютерной анимации с возможностью получения диаграмм зазоров. Следовательно, выбор математического аппарата и системы представлений операторов преобразований сборочного пространства должен быть связан с общим определением применяемых тензоров и метрических тензоров. Требуемые понятия введем таким образом, чтобы и линейная функция, и билинейная функция, и линейный оператор преобразования в сборочных операциях производства изделий авиационной техники, называемый тензором второго ранга, и многие другие линейные и полилинейные отображения одного сборочного пространства в другое в общей иерархической структуре можно было включить в единое понятие тензора и оператора преобразований. Тензоры в этом случае отличаются друг от друга типом и рангом. При рассмотрении различных отображений введем следующую компактную запись:

ϕ : Р>Q . (1)

1) В этой записи Р – множество элементов сборок, которое отображается в множество Q, где Q – сборки последующих уровней сложности, ц – отображение, сопоставляющее элементу р ∈ Р элемент q ∈ Q : ϕ(р)=q. Если отображение ц линейное (полилинейное), будем отмечать его надписью над стрелкой. Запись (1) эквивалента утверждению: отображение ц сопоставляет элементу из пространства (множества) Р элемент из пространства (множества) Q. Состав технологических операторов, реализуемых в процессе сборки, имеет иерархическую структуру. На верхнем уровне технологические операторы различаются по видам работ: например, при узловой и агрегатной сборке технологический процесс включает в себя операции выполнения соединений в пространстве сборки по контурам соединения. Эти особенности выполнения операций сборки связаны с местом контуров, реализуемых тем или иным технологическим оператором, в структуре контуров сборочной единицы. Поэтому при детальном анализе последовательности выполнения технологических операторов сборки необходимо вместо обобщенного отношения рассматривать эти отношения применительно к отдельным контурам сборочной единицы А или входящих в нее элементов aiО A. Для этого разделим контуры F (А) на две группы:

F (А)⁰ — совокупность контуров сборочной единицы в целом, т. е. таких, где каждому контуру F_j О F(А)⁰ соответствует конструктивное тело (A_j), включающее в себя не менее двух элементов конструкции, входящих в сборочную единицу;

n 0

F ⁽ A ) ^ = U F ⁽ a i ) - совокупность контуров i =1

отдельных элементов конструкции сборочной единицы, рассматриваемых независимо от кон- туров других элементов.

Поскольку контуры F (А)^э состоят из подмножеств контуров F (a_i)⁰ отдельных элементов конструкции сборочной единицы, последовательность реализации всей группы контуров F (а_i)⁰ среди контуров F (А) сборочной единицы соответствует последовательности установки элементов А. В состав F (а_i)⁰ входят контуры формы и положения элемента a_i, а также контуры, подлежащие доводке (доработке) в процессе установки а_i О А. Состав и последовательность операторов реализации этих контуров в процессе установки можно определить по табличным, сетевым или перестановочным моделям. Применение сетевых моделей обычно требует детализации особенностей выполнения сборочных операций. Пример одной из таких моделей показан на рис. 1. Реализация же каждого множества F

a)_____________________________________________________________________________6)

Операция		Fj									Fj
			F,	Рз	f4	f5	F6	F,	f8	F9	т	F,	^2
Предварительная установка листа для пригонки	т	1										1	1
Разметка мест доработки по контуру	т		1									1	1
Разметка мест доработки по сопряжениям	т		1								^3	1	1
Выемка листа из приспособления	т			1								1	1
Обрезка припуска пневмоножницами	т				1						Г5	1
Снятие припуска пневмофрезой	т					1							1
Снятие припуска пневмошарошкой черновой	т				1	1						1	1
Снятие припуска пневмошарошкой чистовой	т						1					1	1
Зачистка заусенцев по кромкам	т							1			T9		1
Нанесение грунта по кромкам	т								1		T10		1
Установка листа окончательная, проверка сопряжений	т									1	^11	1	1

Рис. 1. Сетевая модель операций установки листа обшивки:

а — дизъюнктивная матрица контуров; F1 — контур положения листа для разметки; F2 — контур разметки; F3 — контур положения листа для доработки; F4 — контур припуска, д Ј 2 мм; F5 — контур припуска; 3Ј д?Ј4 мм; F6 — чистовой контур припуска; F7 — контур заусенцев, 3 Ј6 Ј 4 мм; F8 — контур защитного покрытия кромки, 3Ј д Ј4; F9 —контур положения листа; б — конъюнктивная матрица контуров; F1 — контур листа, д Ј мм; F2 — контур листа, 3 Ј д Ј 4 мм; в — граф взаимосвязи операторов

(a_i)⁰ контуров как единого целого рассматривается как этап, соответствующий одному обобщенному оператору установки элемента a_i О A ; последовательность операторов установки можно определять по табличным или сетевым моделям (при использовании типовых технологических процессов установки) или перестановочным моделям (при проектировании единичных технологических процессов).

Окончательно в состав контуров F (А)⁰ сборочной единицы входят контуры всех конструктивных соединений, контуры герметизации, защитных покрытий и другие, относящиеся к сборочной единице в целом. Структура каждого, контура соединения достаточно сложна, поэтому состав и последовательность: операторов для них определяют по табличным или сетевым моделям, картам технологической документации. Выполнение принципа системного единства при синтезе структуры технологической системы по структурным математическим моделям, а численных расчетов – по аналитическим моделям обеспечивает их адаптацию к различным видам вычислительной техники.

Тогда ТП сборки по глубине структурирования представляется или как неструктурированный объект A в виде единого целого, или как система взаимосвязанных элементов одного уровня, или как многоуровневая иерархическая система. Соответственно по степени абстрагирования ТП моделируется на уровнях теоретикомножественных методами теории множеств и теории графов, логических методами математической логики и количественных по расчетным свойствам и отношениям. При этом группируются данные трех типов: данные о компонентах объекта моделирования в виде множества компонент самого объекта A , множество F контуров как свойствах объекта и множества R отношений между компонентами и контурами. Так как понятие контура является обобщающим для таких понятий, как свойство, признак, характеристика, параметр, критерий, то с математической точки зрения логично одни и те же объекты, свойства и отношения рассматривать или как теоретико-множественные As, Fs, Rs, или как логические Ah, Fh, Rh, или как количественные AN, FN, RN величины и отношения. Переход с одного уровня на другой осуществляется регламентированными способами с использованием межуровневых отношений, с указанием границ и условий перехода одних величин и отношений в другие. На теоретико-множественном уровне моделируются состав компонент объекта A в виде упорядоченного или неупорядоченного множества A = (a1,a2,...,an) . Моделирование состава компонент объекта A на теоретико-мно- жественном уровне производится в виде упорядоченного или неупорядоченного множества A = (a1,a2,...,an); состава его контуров как F(A) = (F,F2>->Fm). Наэтом же уровне моделируются составы контуров как F (ai) с F ( A ) компонент объекта A и задаваемые бинарные отношения Rs между компонентами и контурам, к которым относятся бинарные отношения иерархической подчиненности, смежности и порядка, обусловленные структурными, функциональными, информационными и другими связями между компонентами и контурами объекта как технологической системы, где можно выде- лить следующие подмножества:

• -    подмножество R^- ( A ) отношений между компонентами объектами A ;

• -    подмножество R^- ( a i ) отношений между a_i и другими компонентами A ;

• -    подмножества ^R- ( ^F ( A ) ) и R^- ( F ( a i ) ) как отношений между контурами F ( A ) и F ( a i ) ;

• -    подмножества R - ( F j ( A ) ) и R ( F , ( a ) ) как отношений между контурами F_j и другими контурами F ( A ) или F ( a i ) ;

• -    множество отношений R^- ( A , F ( A ) ) как отношений между компонентами и контурами объекта A .

Бинарное отношение R- (A) описывается либо графом G = (A, C) , либо булевой матрицей |с. (j )| |A смежности вершин этого графа; эта мат- рица представляет собой подмножество декартова произведения A х A : ||ci (j) ||A — [A х A] с A х A. в записи [A х A] первый символ соответствует мно жеству строк, а второй символ – множеству стол

-

-

бцов булевой матрицы || c i ( j )|| A . Каждая i -ая строка (столбец) матрицы рассматривается как представление бинарного отношения R^- ( a i ) между a i и элементами ( a ^ , a i 2 ,.. a i n - _ 1 ) , для которых элементы строки (столбца) матрицы равны единице. Аналогично описываются бинарные отношения R^- ( F ( A ) ) между контурами объекта A (в виде булевой матрицы |^ F ( A ) х F ( A ) ^| ), бинарные отношения R^- ( F ( a i ) ) между контурами элемента a i (в виде булевой матрицы [^ F ( a i ) х F ( a i ) ^| ) и т.п.

Бинарное отношение R- (A, F (A)) описы- вает составы контуров элементов A это отношение представляют булевой матрицей

I i ⁽ j )l L , F ( A )

матрицей контуров.

Множество C элементов булевой матрицы или дуг графа рассматривают как объект с составом контуров F ( C ) . Между элементами C и контурами F ( C ) также возможны бинарные отношения, которые группируются в подмножества R s ( C ) , R s ( с , ) , R s ( F ( C ) ) , R s ( F_j ( C ) ) , R ( F ( с )/ R s ( F ( с , ) ) , R( C^JF ( C ) ) .

На логическом уровне все объекты, их эле- менты и контуры рассматриваются как логические величины. Каждому множеству, булевой матрице или графу соответствуют наборы логических отношений между входящими в них элементами, представленными в виде логических переменных. Множеству A соответствуют логические отношения RL ( A) вида A = RL (a,,a,,...,an) между объектом a и его элементами. Одним из наиболее часто используемых при проектировании отношений такого вида является описание условия, определяющего возможность вхождения a, е A в подмножество Ak с A элементов, обладающих заданными свойствами. Между ai и другими элементами A возможны логические отношения RL (a,) ; примерами этих отношений являются логические условия существования ai при наличии или отсутствии других элементов A . Множеству контуров соответствуют логические отношения RL (F(A)) и RL (F,(A)) между контурами объекта A и отношения вида RL (F(а,)) и RL (Fj(a,)) между контурами элемента ai . Для столбцов матрицы (2.5) отношения RL (F, ( A)) имеют специфический вид

F , ( A ) = R L ( F , ( a , ) , F j ( a , ) ,..., F ( a , ) )

И определяют логическую связь между истинностным значением контура F , ( A ) объекта A в целом и контурами F , ( a , ) элементов в случае, когда контуры F , ( a , ) являются основными частями F j ( A ) .

На основе такого анализа определяется перспективная структура проектируемого объекта и строится модель порождающей среды, в которой будет осуществляться синтез этого объекта. Порождающая среда включает в себя данные о предметной области, к которой относится объект, о существующих и разрабатываемых структурных моделях объекта, известные или прогнози- руемые отношения и связи между элементами и свойствами объекта и внешней средой. На базе этих данных создается математическая модель, охватывающая ту информацию о порождающей среде, которая может быть формализована и представлена средствами системы математичес- кого моделирования объектов. С целью унификации средств обеспечения САПР отношения RS (A), RS (F (A)), RS (A, F (А)) и другие путем эквивалентных преобразований могут быть приведены к регламентированному виду. В результате структурные модели порождающей среды превращаются в типовые математические модели системы математического моделирования, на основе которых создаются унифицированные компоненты математического, информационного и программного обеспечения САПР.

Отличительной особенностью такой системы является полное отделение математических моделей и алгоритмов проектирования от семантического содержания данных о конкретных объектах проектирования, что позволяет использовать одни и те же математические модели и алгоритмы для проектирования разнородных объектов. Это позволяет создавать типовые математические модели порождающей среды, инвариантные к конкретным объектам проектирования.

Математическая модель S (А) объекта А в общем случае имеет вид

S (A) = { A, F, R } , где A — множество элементов; F — множество контуров; R — множество отношений.

В этой модели A есть отображение элементов реального объекта А , F — отображение контуров F и R — отображение отношений между элементами и контурами объекта А. В состав контуров модели наряду со свойствами элементов объекта, входят свойства, характеризующие взаимодействие объекта с внешней средой: F_вх — входные данные, F_вых — выходные данные, F_упр — управляющие воздействия, F_воз — возмущающие воздействия. Некоторые элементы модели S(A) в конкретных случаях могут быть представлены в неявном виде или вообще отсутствовать. Отсутствующий элемент модели представляют как пустое множество, например, А = О/ или F_вх = О/ , F_упр = О/ . Модель S (А) порождающей среды служит для проектирования объектов А_k с составом элементов A k ^с А. Одна модель 5 (A) порождающей среды содержит данные о множестве { А₁, А₂, … А_N } проектируемых объектов. Построение такой модели основано на свойствах эквивалентности элементов а_i О A , входящих в различные объекты.

Все задачи структурного проектирования объектов и процессов, связанные с определением состава элементов (операторов) и их взаимосвязи, могут быть сведены к шести типовым задачам определения структуры процесса или объекта (рис. 3).

Особенно важное значение при автоматизированном проектировании имеют модели, отражающие структуру объектов проектирования. Каждая такая модель S (А) содержит состав эле-

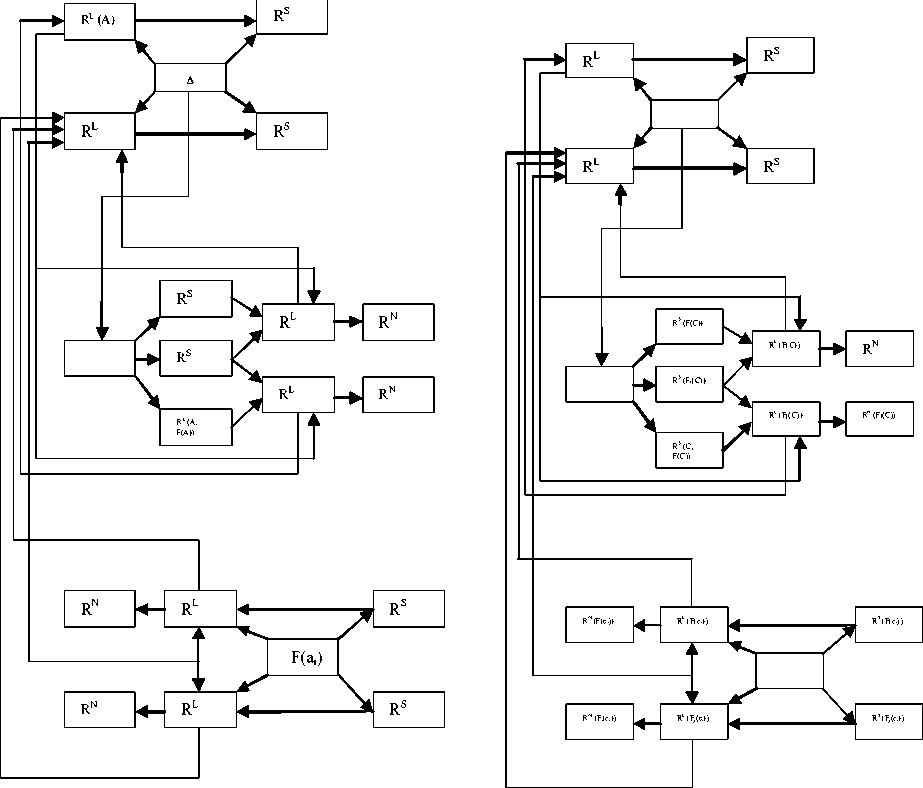
Рис. 2. Взаимосвязь теоретико-множественных, логических и количественных свойств и отношений в иерархической системе математического моделирования объектов на различных уровнях абстрагирования

ментов A, входящих в проектируемые объекты Аk, матрицу контуров (2.5), теоретико-множественные логические и количественные отношения между элементами A и контурами F (A), определяющие состав и все свойства проектируемых объектов Аk. Структурные модели порождающей среды классифицируются в зависимости от способа задания отношений смежности и порядка между элементами модели S (A), отношений смежности и порядка элементов проектируемого объекта Аk, а также состава и числа элементов в различных вариантах Ah. Если отношение смежности между элементами модели задано в виде графа G=(A, С), то модель будет связанной, а если граф G = (A, С) не задан, то модель будет несвязанной. В зависимости от наличия отношений смежности и порядка между элементами проектируемого объекта Аk все модели порождающей среды разделяются на сочетательные, и упорядочивающие. Сочетательные модели применяются в тех случаях, когда определяется только состав элементов проектируемого объекта, а упорядочивающие — когда опре- деляется и состав, и структурные отношения между элементами проектируемого объекта. Как уже отмечалось выше, развитие прикладной теории математической логики при формализованном описании сборочного пространства предполагает, что после функционального выделения свойств компонент структурных моделей они не зависят от смыслового содержания конкретных объектов моделирования. Поэтому приведенная классификация сочетательных и упорядочивающих моделей распространяется на все виды структурных моделей, модели изделий S (А), технологических и производственных систем S (Р), технологических операторов S (Т), средств оснащения производства S (П) и т. д. Теоретикомножественный и логический уровни моделирования объектов в иерархической системе математического моделирования объектов на различных уровнях абстрагирования удобны для автоматизации решения задач структур проектирования, когда с математической точки зрения изучаемый на любом уровне абстрагирования объект A имеет один и тот же прообраз A ,

Задачи структурного проектирования		Типовые математические модели
		А 6		и		40		Л 43 о 40 £		40     , 3		40 —। О X ft		40 rrj 5 ft
			1 &	8	1	5	£	8	1	5	1 &	3	1	s	1
		1	2	3	4	5	6	7	8	9	10	11	12	13	14
Поиск единственного состава операторов	1	1	1			1	1	1	1			1	1
Определение Вариантов состава операторов	2			1	1					1	1				1
Выбор состава операторов	3				1						1				1
Поиск единственной последовательности операторов	4					1	1
Определение вариантов последовательности операторов	5							1	1	1	1		1		1
Выбор последовательности операторов	6								1		1		1		1
Поиск единственного состава элементов	7	1	1			1	1	1	1			1	1
Определение вариантов состава элементов	8			1	1					1	1			1	1
Выбор состава элементов	9				1						1				1
Поиск единственного состава связей	10					1	1
Определение вариантов состава, связей	И							1	1	1	1		1		1
Выбор состава связей	12								1		1		1		1

Рис. 3. Типовая задача структурного проектирования

адекватный реальному объекту. В общем случае, для построения структурных моделей объекта проектирования вначале необходимо установить состав свойств контуров, по которым могут быть выделены элементы проектируемого объекта. Состав этих свойств определяется, в первую очередь, назначением объекта и его функциями. Далее устанавливается природа отношений, связывающих элементы и их контуры (геометрические, механические, функциональные и другие связи).

Для повышения эффективности автоматизированного проектирования логические отношения между элементами и контурами модели порождающей среды и проектируемых объектов приводят к регламентированному виду, отражающему реальные свойства этих объектов. Так, зависимость между составами элементов проектируемого объекта и порождающей среды выражается отношением R^L (А_k) в следующем виде.

Если А_k должен содержать фиксированный набор элементов а е A, то

m

Ak = a ц Л ak2 л ••• akm = л a к,. ; (2) 1                2                      m i = 1 i если Ah может содержать любой элемент а. е A, то

Ak = a 1 v a 2 v ... an = v ak ;(3) i = 1 i если Аk может содержать только какой-нибудь единственный элемент аi , то

n

^Ak = a 1 ^V a 2 ^V ••• a n = ^V a k_t . (4) i = 1 i

Если в Ak должны входить наборы из п групп элементов вида (3), то nm

Ak = л I v a

i = 1 ( i = 1

,

а если из п групп элементов вида (4), то

A

k

nm

л V a i = 1 ^ i = 1

Если А_k может содержать любые наборы групп элементов вида (2), то

A

k

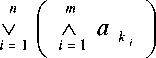
а если любые наборы из групп элементов вида (4), то

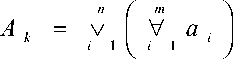
Если A_k может содержать только какую-либо единственную группу элементов вида (3), то

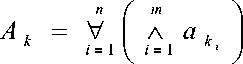
а если единственную группу элементов вида (4), то

A

k

nm

V v a i = i ^ i = i

В общем случае зависимость между составом контуров F (Ak) и контурами порождающей модели выражается отношением RL (F (Ak)). Эта зависимость по составу сентенциональных связок и смысловому содержанию аналогична отношениям упорядоченного множества контуров соорочной единицы. Аналогично описывается зависимость RL (F (аi )) между независимыми контурами F (аi). Отношения между Fj (А) и одноименными контурами Fj (аi) элементов А ко виду и смысловому содержанию также аналогичны отношениям в контурах более высокого уровня согласно схемам узловой или агрегатной сборки. Рассмотренные отношения характеризуют логические связи между элементами и контурами проектируемого объекта Ah и модели порождающей среды. Если реальные отношения RL (A), RL (аi), RL (F (A)), RL (F (аi )), RL {Fj (А)) имеют другой вид, то путем чисто формальных преобразований их можно привести к регламентированному виду. Использование логических отношений регламентированного вида расширяет возможности унификации компонентов математического обеспечения САПР.

ЗАКЛЮЧЕНИЕ

Для обеспечения всего цикла конструирования изделия необходимо обеспечить разработку всех конструкторских данных (проектные данные, схемная документация, электронные макеты, двухмерные чертежи и технические руководства) в электронном виде с применением соответствующих программных продуктов, интегрированных в единой системе управления проектными данными. Создание электронного макета и математического аппарата с построением матриц соединений и матриц перемещений с соответствующими операторами обеспечивает:

• -    глубокую проработку и увязку конструкции самолета уже на этапе проектирования;

• -    переход к бесплазовому производству, исключение трудоемкой и длительной плазовой увязки;

• -    “сборку с первого раза”, обусловленную глубиной проработки проекта при условии соответствующей организации производства;

• -    возможность отказа от необходимости постройки физических макетов;

• -    возможность организации параллельных процессов в проектировании изделия и подготовки его производства;

• -    управление составом изделия и его модификациями;

  - подготовку информации для разработки и поставки электронных устройств по эксплуатации и обслуживанию изделия с учетом модификаций и исполнения.