Теория принятия решений в задачах энергоэффективного управления электроприводом с двигателем двойного питания

Технические системы, к которым относится и регулируемый электропривод (ЭП), являются наиболее активными элементами производительных сил общества и постоянно совершенствуются и усложняются. При этом важным аспектом функционирования технической системы является организация ее управления. Алгоритмы управления системой направлены на достижение целевых показателей в условиях различных ограничений – технических, организационных, экономических и т. д. Эта задача может быть разрешена различными альтернативными методами, наличие которых обусловлено большим количеством факторов, влияющих на результат, а также принятыми критериями эффективности. Различные сочетания этих факторов образуют множество допустимых решений по управлению системой [1]. В связи с этим задачей теории принятия решений является поиск наилучшего управления при известных ограничениях, возможных противоречиях и перспективных проблемах.

Современное развитие промышленного производства требует все более широкого внедрения регулируемого электропривода переменного тока. Но самые распространенные общепромышленные приводы имеют в своем составе частично управляемые базовые машины, не в полной мере отвечающие требованиям в отношении энергоэффективного управления [2].

В наибольшей степени этим требованиям отвечает ЭП с асинхронизированным вентильным двигателем (АВД), который можно отнести к классу управляемых электрических машин. Данный вариант двигателя двойного питания (ДДП) имеет статические преобразователи частоты в статорной и роторной цепях [3]. Это позволяет организовать четыре канала управления приводом – частотой вращения вала, магнитным состоянием электриче- ской машины, реактивной мощностью и активными потерями [4].

Функциональная схема организации многоканального управления электроприводом с ДДП представлена на рис. 1.

В результате глубоких теоретических исследований данного варианта электропривода были синтезированы алгоритмы энергоэффективного управления ДДП, исследовано влияние частоты возбуждения и способа аппроксимации кривой намагничивания на энергетические показатели двигателя [5]. Значения этих показателей существенно зависят и от режима работы двигателя. Результаты анализа эффективности возможных алгоритмов управления ДДП представлены в таблице.

Актуальность проблемы

Работа двигателей в составе регулируемого электропривода сопряжена с появлением дополнительных потерь от высших гармоник несинусоидальных фазных токов и напряжений. Наличие высших гармоник приводит к возрастанию нагрева двигателя, снижению мощности и электромагнитного момента на валу. Кроме этого, в асинхронных ЭП с частотным регулированием при изменении питающего напряжения методом ШИМ повышают частоту модуляции для улучшения гармонического состава напряжения, что ведет к возрастанию потерь на коммутацию в силовых ключах, которые определяют нагрев элементов ПЧ (напомним, что гом зависят от выбранного метода ШИМ [6–8]. Стратегия формирования фазных токов двигателя определяет их гармонический состав, оказывающий, в свою очередь, влияние на потери и нагрев элементов электрической машины [9–11]. В работе [12] проведен глубокий анализ потерь в элементах преобразователей частоты и установлено, что реализация алгоритма минимума суммарных по-

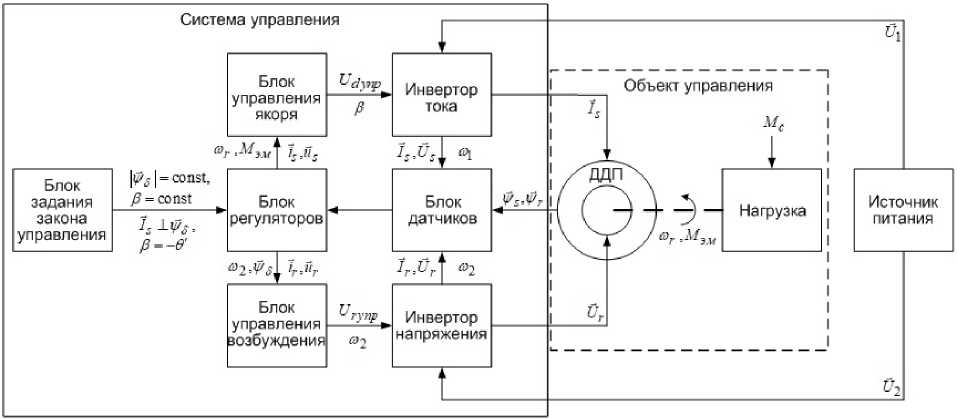
Рис. 1. Функциональная схема системы управления ЭП с ДДП

Fig. 1. Functional diagram of the control system for an electric drive with a double-fed motor

Анализ эффективности алгоритмов управления электроприводом с ДДП The efficiency of control algorithms for an electric drive with a double-fed motor

Алгоритмы энергоэффективного управления

о 8 с II м « й' 3 S

7 s' ю 11 ^ 3

"К Q § s'

S' l"'"Hl 3 ■ S и 8 §

s 3

11 g? и s

й J 3^ 'L^ 3

11 s

& о ° с II ='=

►< о H ii ^-i s

8 о 3 и 11 3 e-

8 s

Диапазон скоростей

Диапазон нагрузок

0,25ω ен

0,3 M эмн <

+ х

– х

– х

+ х

– х

– х

– х

– х

– х

– х

0,3 < M эм <  1

+ х

+ х

± х

+ х

– х

– х

– х

– х

1 <  M эм <  2

+ х

+ х

+ х

+х

± х

± х

± х

± х

+ *

± х

± х

+ *

ω ен

0,3 M эмн <

+ х

– х

– х

+ х

± *

– х

– х

± *

– х*

– х*

0,3 < M эм <  1

+ х

+ х

+ х

+ х

± *

± *

± *

± *

± *

± *

± *

± *

1 <  M эм <  2

+ х*

+ х*

+ х*

+ х*

+ *

+ *

+ *

+ *

+ *

+ *

+ *

*

1,25ω ен

0,3 M эмн <

+ *

– х

– х

+ *

Данные алгоритмы нецелесообразно использовать для этого диапазона угловых скоростей

0,3 < M эм <  1

+ *

+ *

± *

+ *

1 <  M ЭМ <  2

+ *

+*

± *

+ *

Примечания:

«+» – алгоритм эффективен по суммарным потерям в двигателе;

«–» – алгоритм неэффективен по суммарным потерям в двигателе;

«±» – алгоритм обеспечивает приемлемую эффективность по суммарным потерям в двигателе;

«*» – алгоритм эффективен по сочетанию КПД и cosφ Σ ;

«х» – алгоритм неэффективен по сочетанию КПД и cosφ Σ ;

«х*» – алгоритм обеспечивает приемлемую эффективность по сочетанию КПД и cos φΣ.

терь в асинхронном двигателе обеспечивает и минимальные потери в элементах ПЧ.

Поскольку энергетически эффективные алгоритмы управления АВД призваны обеспечить минимум фазных токов в любых режимах работы привода, то их реализация позволяет снизить потери и в элементах его ПЧ. Габаритная мощность преобразователя будет минимальна при минимуме потерь в двигателе и отсутствии потребления реактивной мощности. Это возможно в электроприводах с АВД и с ВД постоянного тока при электромагнитном возбуждении [13].

Из сказанного выше очевидно, что предложенные алгоритмы энергоэффективного управления ЭП с ДДП и известные стратегии ШИМ в ПЧ оказывают влияние не только на потери в элементах привода, но и на их тепловые режимы, которые являются основными факторами надежности функционирования системы. Для оценки этого влияния на температуру элементов привода необходимы их адекватные тепловые модели, топология и подбор параметров в которых не является тривиальной задачей и зависит от электрических характеристик и механической конструкции силовых устройств, в том числе радиаторов и системы охлаждения [14, 15].

Большинство существующих тепловых моделей основаны на простом методе эквивалентных цепей с сосредоточенными параметрами. Применение этих моделей не вызывает затруднений, однако из-за упрощённого и/или недостаточного описания тепловой цепи ротора и представления распределения температуры равномерным они могут предоставлять данные, не соответствующие действительности [16]. Ввиду своей простоты они могут быть интегрированы в систему защиты от перегрева двигателя [17, 18]. В качестве альтернативы для построения тепловой модели может использоваться метод конечных элементов, который позволяет вычислять пространственное распределение тепла [19, 20]. Построение таких моделей и инструменты их анализа ограничиваются функционалом программной среды, вычислительными ресурсами и исходными данными о двигателе. Полученная точность расчётов модели может не соответствовать трудозатратам на её разработку и времени моделирования [16].

В идеальном случае система управления ЭП с ДДП должна осуществлять автоматический выбор наиболее энергоэффективного алгоритма управления и метода ШИМ в том или ином режиме работы привода на основе результатов текущих измерений, позволяющих оценить достигаемые значения целевой функции энергетического критерия и температуры элементов системы. Однако практическая реализация такого варианта системы управления будет иметь чрезвычайно низкое быстродействие и не сможет удовлетворить требования по динамике для приводов с частыми сменами режима функционирования в рамках технологической задачи.

Второй путь синтеза системы управления при проектировании электропривода заключается в

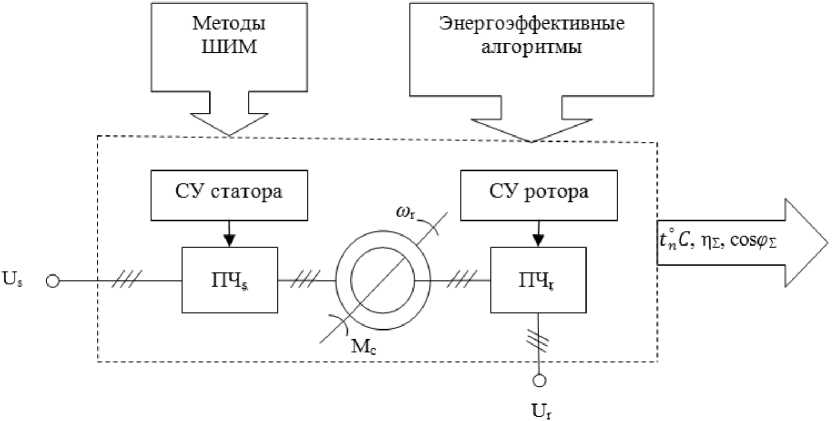
Рис. 2. Структурная схема системы управления ЭП с ДДП

Fig. 2. Block diagram of an electric drive control system with a double-fed motor

реализации заранее определенных оптимальных соотношений координат двигателя на основе измерения мгновенных значений переменных параметров объекта управления, определяющих эти координаты. Структурная схема ЭП с ДДП, отражающая этот подход к проектированию, представлена на рис. 2. Здесь СУ ПЧ в цепях статора и ротора реализуют один из указанных в таблице алгоритмов управления с использованием одной из стратегий ШИМ для достижения наилучших значений суммарных энергетических показателей η_Σ, cosφ_Σ и температуры t n °C элементов привода в условиях выполнения им технологической задачи (известных значениях скорости ω _r и нагрузки на валу М _с).

Кроме указанных критериев оптимальности при проектировании ЭП могут представлять практический интерес и такие, как массогабаритные показатели, первичные капитальные затраты, сроки окупаемости и т. д.

Обозначенная проблема проектирования ЭП с ДДП может быть отнесена к классу многокритериальных детерминированных статических задач теории принятия решений, когда установленные критерии оптимальности и имеющиеся ограничения не зависят от времени, а для каждого выбранного энергоэффективного алгоритма управления и метода ШИМ еще до их применения известно, что будет достигнут некоторый определенный результат.

При этом количественные показатели критериев оптимальности и зоны ограничений определяются исключительно выбранной разработчиками стратегией, а также фиксированными детерминированными факторами, полностью известными им.

Постановка задачи

Для определения направления дальнейших исследований сформулируем обобщенную постановку многокритериальной детерминированной статической задачи принятия решений в терминах, принятых в [21].

Пусть имеется необходимость осуществления некоего управляемого мероприятия, результат которого зависит от выбранной оперирующей стороной стратегии и ряда неслучайных фиксированных факторов, характеризующих условия прохождения мероприятия, свойства участвующих в нем объектов и полностью известных оперирующей стороне. Символом X обозначим выбранную стратегию. Для различных частных случаев X может быть скалярной или векторной величиной, матрицей или еще более сложным образованием. Примем, что реализуемая стратегия является n -мерным вектором

Х = ( X ! , X ₂,^, X „ ) = ( Xj),jel,H. (1)

На компоненты x j вектора управления Х могут налагаться ограничения, обусловленные существом решаемой задачи. В общем виде ограничения могут быть записаны как условия

9i = gi⁽Ct,X) >  b_t,i e 1,m, (2) где g_t - некоторая функция; b[ - фиксированная скалярная величина; C_t - некоторая совокупность фиксированных скалярных или векторных величин.

Ограничения (2) определяют для стратегии Х область допустимых значений Ω Х , из которых оперирующая сторона выбирает одну из стратегий для достижения ожидаемого результата управляемого мероприятия.

Эффективность выбранной оперирующей стороной стратегии можно оценить совокупностью критериев e 1 , e 2 , …, e k , важность которых для результата управляемого мероприятия различается своими коэффициентами относительной важности λ 1 , λ 2 , …, λ k .

Локальные критерии eq, q e 1,к образуют вектор критериев E = (eq), а коэффициенты λq – вектор важности Λ = (λq). Каждый из локальных критериев, скалярных или векторных, характеризует некоторую локальную цель управляемого мероприятия и связан со стратегией некоторым отображением eq = eq(Aq,X), q е 1, к, (3) где Аq – некая совокупность фиксированных факторов. Частный случай отображения Х → eq – функциональная зависимость между критерием eq и стратегией.

Отображения e_q, q е 1, к задаются аналитически, таблично, графически, алгоритмически, наконец, эвристической процедурой в самом сложном случае. Будем считать, что каждый локальный критерий e q является скалярной функцией стратегии Х и задан аналитически. Тогда вектор критериев E = ( e q ), q е 1, к будет представлять собой вектор-функцию от стратегии Х

Е = (e q (A q ,X)). (4)

Очевидно, что целью лица, принимающего решение при проведении управляемого мероприятия, будет достижение возможных минимаксных значений всех локальных критериев эффективности e q . Достичь цели операции возможно выбором стратегии Х из области ее допустимых значений Ω _Х .

Но одновременное достижение цели по всем локальным критериям за счет выбора одной из возможных стратегий является неразрешимой задачей. Руководитель мероприятия стоит перед выбором некоего компромисса в достижении локальных целей мероприятия и должен определить оптимальную стратегию X , зависящую от двух условий:

– выбранная стратегия X должна быть осуществима, т. е. должна принадлежать области ее допустимых значений Ω Х ;

– стратегия должна быть наилучшей с точки зрения принятого принципа компромисса с учетом вектора Λ важности локальных критериев.

Выбранная стратегия должна удовлетворять условию

Е = Е ( Х = opt [ Е ( Х , Л]. (5)

Х EQ х

Здесь символами X и E обозначены оптимальное значение стратеги Х и соответствующее ей оптимальное значение вектора эффективности Е ; символ opt – оператор оптимальности, представляющий собой математическую модель принятого при решении задачи принципа компромисса между локальными критериями.

Этапы решения поставленной задачи

Рассматривая проблему проектирования ЭП с ДДП в рамках приведенной выше постановки многокритериальной задачи принятия решений, можно отнести ее к типу задач оптимизации на множестве целей, каждая из которых должна быть принята во внимание при выборе стратегии управления. Особенностью задач этого типа является тот факт, что локальные критерии имеют различные единицы измерения. Это приводит к необходимо- сти нормализации критериев – приведения их к единому масштабу, в идеальном случае безразмерному. Проблема носит концептуальный характер и для ее разрешения необходимо проведение различного рода эвристических процедур с приме- нением экспертных оценок.

Кроме этого, имеется еще ряд специфических проблем, к числу которых относится определение области компромисса, в которой существует про- тиворечие между некоторыми критериями и улучшение качества одних ведет к ухудшению других. Практически важным результатом при решении этой проблемы будет сужение области для поиска возможных решений.

Последующее нахождение наилучшего решения в определенной области компромисса может осуществляться только на базе некоторой схемы компромисса. Количество возможных вариантов достаточно велико и выбор рабочей схемы также является сложной концептуальной проблемой. Определение схемы компромисса раскрывает смысл оператора оптимизации opt в соотношении (5) в виде opt Е(Х) = opt Е(Х) = max ф(Е(Х)), (6)

хе^х хейх хе^х где φ(Е) – некоторая скалярная функция от вектора критериев Е.

Следовательно, осуществив выбор одного из принципов оптимальности, мы сведем векторную задачу принятия решения к эквивалентной скалярной задаче. Выполнение этого этапа является объективной необходимостью для любой векторной задачи принятия решения, так как реализовать фактически можно лишь однокритериальную оптимизационную схему [21].

Не менее важной является проблема установления приоритета локальных критериев, которые в многокритериальной задаче имеют различную важность и для установления приоритета должны быть нормализованы.

Применительно к задаче синтеза системы управления ЭП с ДДП проблема установления приоритета критериев может быть интерпретирована следующим образом: что является более важным – соблюдение температурного режима элементов привода или достижение экстремальных энергетических показателей при заданных значениях частоты вращения вала и нагрузки?

Равенство или превосходство в важности одного критерия над другим основано на сравнении по предпочтительности векторных оценок специального вида. Методы установления приоритета критериев являются предметом математической теории выбора критериев и рассмотрены в [22].

Последовательное устранение указанных выше проблем, связанных с выполнением многокритериальной задачи принятия решений, а именно – нормализация локальных критериев, определение области компромисса, выбор схемы компромисса и соответствующего принципа оптимальности, учет приоритета критериев, – позволит свести векторную задачу принятия решения к эквивалентной скалярной задаче. И на этом этапе также возникают некоторые проблемы, как правило, вычислительного характера, связанные в основном с алгоритмизацией нахождения наилучшего решения.

Вывод

Проблема проектирования регулируемого электропривода на базе ДДП с реализацией алгоритмов энергоэффективного управления и контролем теплового состояния элементов привода может быть отнесена к классу многокритериальных детерминированных статических задач теории принятия решений. Практический интерес при разработке системы ЭП могут представлять и та- кие критерии оптимальности, как массогабаритные показатели, первичные капитальные затраты, сроки окупаемости и т. д. Обобщенная постановка многокритериальной детерминированной статической задачи принятия решений определяет ряд концептуальных проблем, связанных с ее выполнением: необходимость нормализации локальных критериев, определение области компромисса, выбор схемы компромисса и соответствующего принципа оптимальности, учет приоритета критериев. Последовательное устранение этих проблем позволит привести векторную задачу принятия решения к эквивалентной скалярной задаче, которая может быть решена практически. Возникающие на этом этапе проблемы носят вычислительный характер и связанны в основном с алгоритмизацией нахождения наилучшего решения.