Теория случайных антенн: атрибуты и отличительные особенности

Проиллюстрировать как общность, так и различие между традиционной теорией антенно-фидерных устройств (АФУ) [1] и статистической теории антенн (СТА) [2], одним из актуальных направлений развития которой является теория случайных антенн (СА) [3], можно на примере атрибутов (характеристик и параметров) теории АФУ.

Первой среди них, безусловно, является характеристика направленности, которую представляют графические изображения ее сечения поверхностями заданного вида – диаграммы направленности (ДН). Назначением ДН является демонстрация угловых распределений уровней электрической Е - и магнитной Н -составляющих электромагнитного поля (ЭМП), создаваемого АФУ на заданном расстоянии, – этот смысл ДН сохраняют в СТА с учетом двух новых обстоятельств.

Во-первых, учет случайных ошибок ведет к необходимости рассматривать вероятностные реализации ДН, которые лучше соответствуют реальным условиям работы АФУ (это же относится ко всем параметрам, определяемым через ДН, – таким, как координаты главного максимума, ширина основного лепестка, уровни боковых лепестков и т.д.) [1-2]. Во-вторых, в каждой точке наблюдения с фиксированными координатами, в дополнение к неискаженным ошибками ДН, появляется возможность исследовать гистограммы случайных уровней ЭМП, найденные, например, методом статистического имитационного моделирования (СИМ), которые отражают влияние на направленность АФУ ошибок любого заданного вида – как порознь, так и совместно [3].

Коэффициенты направленного действия и усиления в СТА также сохраняют прежний смысл, если характеризуют отличия реального АФУ (с учетом наличия ошибок) от эталонного образца, в котором ошибки отсутствуют. Это же относится к таким параметрам, как действующие длина и площадь поверхности, поскольку они характеризуют сравнительную эффективность АФУ и его эталона (который может быть задан в виде физической, математической, электродинамической модели) по критерию уровня ЭМП. Однако никакой новой информации о свойствах АФУ, по сравнению с гистограммами уровней ЭМП, гистограммы случайных значений указанных параметров не несут.

Гистограммы входного сопротивления [4], являющиеся результатом решения внутренней задачи СТА, представляют интерес при формировании исходных данных для решения внешней задачи в части моделирования случайных ошибок [5-6]. Кроме того, найденные расчетно-экспериментальным путем, они могут содержать информацию о характере влияния окружающей среды (местных предметов) на согласование АФУ. По сравнению с традиционной теорией антенн возможности СТА в этом отношении представляются более широкими. То же относится к таким параметрам, как мощности излучения и потерь, коэффициент полезного действия, а также энергетический потенциал активного АФУ [3].

Цель настоящей статьи – анализ отличий методов и средств теории СА от близких ей по области применения разделов радиотехники и компьютерной техники: классической теории АФУ и СТА; теории рассеяния радиоволн на шероховатой поверхности; компьютерного имитационного моделирования и т.п.

Теория СА как развитие СТА: переход от случайных ошибок к неопределенности знаний

Главным отличием теории СА от статистической теории антенн (СТА) является переход от понятия «случайная ошибка» применительно к амплитудам, фазам, пространственным координатам и временным сдвигам, которое является ключевым в СТА, к понятию «неопределенность» [6] применительно к исходным данным (знаниям об СА), необходимым для их исследования. Вопрос об этих ошибках и неопределенностях может быть поставлен следующим образом [7]: пусть система из N сосредоточенных излучателей создает в точке наблюдения М напряженность поля Е_М и мы считаем, что располагаем информацией, которой достаточно для применения формулы

N

Е_м = ^ДХЛ + АЛ; фА-Дф; R + AR; t + Д^ ,(1)

где А и ДА – соответственно, регулярная и стохастическая составляющие амплитуды сигнала, возбуждающего n -ый излучатель; ф и Дф – аналогичные составляющие фазы сигнала, если он является гармоническим; R и ДR – составляющие трехмерной пространственной координаты n -го излучателя; t И Д1 – составляющие модельного времени, используемого при расчетах. Указанные стохастические составляющие именуются в СТА случайными ошибками – соответственно, амплитудными, фазовыми, геометрическими и временными.

Однако неопределенными в (1), строго говоря, являются также и число элементов антенны N, и сам факт суммирования Еn по n, и даже наличие в природе перечисленных регулярных составляющих и ошибок – особенно если мы не уверены, что располагаем достоверной информацией о конструкции антенны и режиме ее работы, как это имеет место при исследовании СА. Поэтому критериями для оценки обобщенной величины

X = х₀ + дх, (2)

моделирующей ошибки всех типов в (1), могут быть абсолютное дх и относительное дх/х₀ значения присущей ей неопределенности. На первоначальных этапах в СТА принималось ДХ/Х₀« 1, затем ДХ/Х₀ « 1, но структура (2) оставалась прежней.

Поскольку сегодня СТА обратилась к изучению СА, приходится решать, что делать: исследовать случай ДХ/Х₀ » 1 или модифицировать всю схему (2), отказавшись от выделения в составе X квазидетерминированной регулярной части ^0 .

Последний вариант представляется не только более радикальным, но и лучшим образом соответствующим природе СА и, что не менее важно, – онтологическим принципам современной теории вероятностей (ТВ) [8]. Рассматривая (1) как результат обобщенного суммирования случайных составляющих Е_n , мы приходим к задаче анализа последовательностей случайных сумм Е_М в условиях применимости центральной предельной теоремы ТВ – в ее традиционном и обобщенном виде [9].

Напомним, что в первом случае решение данной задачи приводит к предельному распределению для Е_М в виде нормального закона, во втором случае – к семейству одномерных устойчивых распределений [8-10], обобщающему нормальный закон. Поэтому наиболее вероятной моделью неопределенности, которую современная ТВ может предложить теории СА, является устойчивый закон [6-7]. При неуверенности в условиях применимости предельных теорем ТВ, а также в отсутствие информации о свойствах неопределенностей в (1) можно руководствоваться «принципом безразличия» и считать их распределенными по равномерному закону [11-12].

Отметим также, что возможности статистического имитационного моделирования (СИМ) по версии метода Димова-Маслова (МДМ) [13] позволяют строить как статические модели, которые сегодня нашли применение при исследовании СА [3; 14-15 и др.], так и динамические – поиск приложения которых в СТА представляется актуальным.

Рассеяние радиоволн на шероховатой поверхности и теория СА

Субъективность понятия неопределенности была отмечена Дж. Кейнсом [16] еще в 1937 г. «Под неопределенностью мы не имеем научного основания, которое могло бы помочь нам сформулировать идею измерения вероятности. Мы просто не знаем. Однако потребность действовать и принимать решения заставляет нас, как практических людей, игнорировать этот неудобный факт и вести себя так, как если бы мы имели хороший утилитарный способ вычисления значений предполагаемых преимуществ и недостатков – каждое из которых умножено на соответствующие ожидаемые вероятности, которые только и ждут, чтобы их просуммировали».

В то же время неопределенность не означает отсутствие информации как таковой: речь идет о неполноте, неточности и неадекватности тех или иных конкретных знаний упомянутых «практических людей». Механизм уменьшения неопределенностей зависит от ряда факторов: таких как методики сбора и обработки исходных данных, выбор способов представления и критериев оценки результатов моделирования, форм их последующего применения и т.п. Причем главным препятствием являются объективные исходные трудности: «чрезвычайно сложно собрать обширную информацию, состоящую из многочисленных серий однородных данных… Приписывать неопределенным по самой своей сути величинам какую-то особую точность бесполезно, применение точных формул к этим слишком неточно определяемым величинам есть не что иное, как обман и пустая трата времени» [17].

Специфику традиционных способов уменьшения неопределенностей покажем на примере задачи о рассеянии радиоволн на статистически неровной (шероховатой по терминологии [1819]) поверхности, решение которой доведено до практического применения в [20]. Структурирование этой задачи имеет в виду три этапа:

• -    формализацию способа возбуждения внешним электромагнитным полем (ЭМП) поверхности S_A , о которой идет речь;

• -    статистическое моделирование неровного рельефа поверхности S _A ;

• -    определение структуры ЭМП, рассеянного поверхностью S _A, в рамках решения внешней электродинамической задачи с использованием принципа Гюйгенса-Кирхгофа.

Каждый из этих этапов непосредственно связан с преодолением неопределенностей, которые в [20], по аналогии с [18-19], преодолеваются следующим образом:

• -    принимается, что поверхность S _A возбуждается ЭМП падающей плоской волны, источник расположен достаточно далеко от нее, а неравномерность возбуждения соответствует двумерной гауссовской кривой с максимумом ЭМП в условном центре зоны облучения;

• -    считается, что статистический рельеф S _A соответствует нормальному закону распределения при гауссовской или экспоненциальной модели корреляционной зависимости для неровностей, отвечающих критерию Релея и приближению Кирхгофа (длина плоской волны много меньше радиуса корреляции поверхности S _A);

• -    геометрия внешней задачи принимается соответствующей рис. 1, где П _пад; П _отр и П _раc – значения уровней плотности потока мощности (модули вектора Пойнтинга), соответственно, для падающей, зеркально отраженной волн и компоненты углового спектра рассеянных поверхностью S _A волн;

• -    результатом аналитического решения внешней задачи являются значения среднего уровня и среднего квадрата уровня напряженности ЭМП, рассеянного неровной поверхностью (см. П _отр и П _раc на рис. 1) на расстоянии от S _A, соответствующем дальней зоне (Фраунгофера) волнового ЭМП.

Перечисленные допущения корректны ввиду того, что в [20] исследуется рассеяние радиоволн декаметрового диапазона (длины волн 10 … 100 м) неровностями Земли на трассах протяженностью 1000 … 4000 км. В ситуациях, соответствующих условиям работы СА, они неприемлемы.

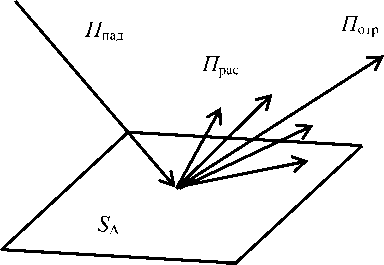
Рис. 1. Лучевая модель рассеяния плоской волны на шероховатой поверхности S _A

В подтверждение этого вернемся к упомянутым трем этапам решения задачи о рассеивающих свойствах поверхности SA, аналогом которой, на первый взгляд, может быть прямоугольная апер- турная СА (далее АСА). Первый этап из сопоставления выпадает полностью, поскольку условия возбуждения АСА являются существенно более сложными и трудноформализуемыми [3; 5; 11-12; 21-22]. На соответствующей АСА поверхности SA необходимо задавать (оценив их расчетно-экспериментальным или иным путем) три ортогональные составляющие (ОС) напряженности электрической Е-составляющей и три ОС магнитной Н-составляющей ЭМП, которое возбуждает АСА. Представлять их в виде плоской волны, соответствующей Ппад на рис. 1, оснований нет.

Второй этап не имеет практического смысла – поскольку излучающая поверхность АСА не является статистически неровной, а промоделировать ее реальную структуру (например, для АСА в виде окна, защищенного фигурной декоративной решеткой) ни возможности, ни необходимости нет. В свете изложенного отпадает и третий этап, предусматривающий аналитическое решение внешней задачи – во-первых, потому что он базируется на выполнении первых двух этапов, во-вторых, потому что доведение соотношений [18-19] до практически приемлемого уровня по аналогии с [20] в данном случае невозможно.

Поэтому необходимо использовать другие способы уменьшения неопределенностей – связанные, например, с применением СИМ по МДМ [13] в сочетании с вербальным и математическим моделированием при использовании принципа Гюйгенса-Кирхгофа.

Гибридные СИМ-модели по МДМ для исследования СА

Метод СИМ является в настоящее время одним из самых универсальных и эффективных средств исследования сложных систем (СС): математики используют его при проведении компьютерных экспериментов, призванных проверить и подтвердить аналитические выкладки. Прикладные специалисты видят в нем средство решения задач, не решаемых другими способами. Системные аналитики применяют СИМ, когда объем знаний об иерархии компонентов (подсистем и элементов) СС существенно меньше знаний о них. Менеджеры заинтересованы в управлении бизнес-процессами с помощью СИМ. Предложение использовать СИМ по МДМ при исследовании СА отвечает этой тенденции в полной мере.

С точки зрения системного анализа, СИМ по МДМ является открытой СС – поскольку допускает совместное применение методов и средств любого моделирования: мысленного, вербального, физического, математического и т.д. [24].

В частности, методика СИМ по МДМ предусматривает разработку математических моделей (ММ) элементов СИМ-модели, без которых дальнейшее моделирование невозможно [3]. Строго говоря, СИМ-модели всегда являются гибридными – при исследовании АСА в рамках вероятностно-теоретического подхода [6-7] это иллюстрируется применением вербальных моделей для описании предметной области СИМ и ММ для определения характеристик АСА с помощью технологии Монте-Карло [11-12].

Идеология СИМ, однако, предъявляет несколько необычные и противоречивые требования к ММ: с одной стороны, они должны быть достаточно корректными и адекватными, с другой стороны – максимально простыми и «прозрачными» для удобства применения и объяснения получаемых результатов. Поэтому как Левша косоглазый умолял государя императора запретить чистить ружья толченым кирпичом, так специалисты СИМ убеждают теоретиков не идти по пути доказательства теорем и лемм, необходимых для доказательства других теорем и лемм, исследовать разрывы и экстремумы комплексных функций, условия на бесконечности, состав бо-релевских множеств и т.п. [28] – поскольку эти элементы СС целиком принадлежат виртуальной среде и не имеют аналогов в среде реальных объектов (неприменимы для исследования и управления СС) [21]. В то же время однозначных предписаний о том, на каком уровне абстрагирования и сложности ММ следует останавливаться, специалисты СИМ не дают – рекомендуя решать этот вопрос в индивидуальном порядке.

Объяснение данному факту дает теория СС – согласно которой на верхних стратах их изучения преобладают абстрактное описание и моделирование сущностей, тогда как по мере понижения уровня страт происходит переход к более конкретным показателям, вплоть до натуральных параметров на самом нижнем – элементарном уровне [27]. Поэтому можно говорить о том, что наиболее строгие и сложные ММ относятся к верхним стратам анализа СА, тогда как упрощенные ММ – к нижним стратам (СИМ по МДМ в этой иерархии находится где-то посередине, осуществляя удобную и эффективную взаимосвязь между ними). Можно также предположить, что совершенно оторванные, на первый взгляд, от реалий жизни и самые абстрактные ММ просто отражают некие неизвестные нам пока что явления и процессы – происходящие за гранью нашего познания и понимания окружающей действительности.

Однако формулировка и определение исходных данных в ММ-задачах все же уводят подчас так далеко от исследуемых объектов, что ценность полученных в итоге – безупречных в математическом отношении – решений бывает невелика. В то же время взаимодействие специалистов на уровне самых простых и понятных им вербальных моделей и ММ оказывается достаточно эффективным – особенно при одинаковом толковании употребляемых ими (иногда весьма своеобразных по форме выражения, на жаргоне и сленге) терминов.

Сегодня здесь имеют место несколько тенденций. Широкое применение ЭВМ в виртуальной среде стимулирует, во-первых, интенсивное развитие способов структурирования и формализации задач, присущих реальной среде, для их адекватного перевода в среду виртуальную [3]. Во-вторых, использование приближенных, численных, квазидетерминированных и т.п. ММ позволяет получать решения с приемлемым уровнем адекватности, «прозрачные» и комфортные для специалистов СИМ. В-третьих, строгие математические методы, логичные и лишенные внутренних противоречий, адаптируются для тестирования разработанных компьютерных СИМ-моделей, которые сами являются СС. В-четвертых, совершенствование программного обеспечения ЭВМ позволяет эффективно общаться с компьютером разработчикам СИМ-моделей, обладающим минимальным стандартным уровнем математических знаний.

Адаптация ММ, а также других методов и средств моделирования к СИМ, однако, должна быть креативной – в качестве примера укажем на кластерный метод учета корреляционных связей между ошибками, реализованный при исследовании СА. Традиционные для СТА и других приложений (см. предыдущий раздел) гауссовская и экспоненциальная модели корреляционной взаимной зависимости случайных ошибок являются аналитическими и могут быть использованы только в СИМ-моделях малоэлементных дискретных СА [25].

Рис. 2. Кластерный метод учета корреляционных связей между ошибками в АСА

Поэтому для многоэлементных СА, включая АСА, был предложен кластерный метод учета корреляции ошибок [7; 11-12] – принцип которого поясняет упрощенная схема на рис. 2. Прямоугольная площадь АСА разделяется на N одинаковых кластеров, в пределах каждого из которых ошибки возбуждения СА считаются одними и теми же. Ошибки в соседних и других кластерах предполагаются взаимно независимыми (некоррелированными). Нетрудно проверить, что увеличение радиуса корреляции ошибок при использовании традиционных аналитических (гауссовской и экспоненциальной) моделей в этом случае соответствует уменьшению числа кластеров, тогда как уменьшение радиусов корреляции – напротив, эквивалентно увеличению N . Горизонтальный и вертикальный размеры отдельного кластера при этом можно трактовать как эффективные значения радиуса пространственной корреляции вдоль соответствующей оси.

Особенности вербальногои эвристического моделирования СА

В настоящее время вербальные и эвристические методы моделирования СА могут быть реализованы на качественно новом уровне – при поддержке действий специалистов СИМ в рамках технологии автоматизированных рабочих мест. Но даже простой обмен мнениями между ними – с применением приближенных ММ, а также физических и вербальных моделей, представляет интерес при проведении СИМ. В качестве примера рассмотрим онтологическую модель ситуации (ОМС) [26], которая была сформирована экспертным путем и согласована по методу Дельфи [27] при исследовании АСА, показанной на рис. 3. Назначение СИМ-модели – проектирование системы активной защиты (САЗ) конфиденциальной информации от утечки через СА [3; 14-15].

Рассматриваемая АСА представляет собой прямоугольное отверстие с размерами Ixh на проводящей поверхности S , центр которого совмещен с началом системы прямоугольных координат X;Y;Z . Эту апертуру возбуждает источник, расположенный в точке с координатами M^Z^ , и нам необходимо найти напряженность поля Е_М в точке наблюдения M_s на поверхности S_M , удаленной на расстояние R_a от поверхности S Д таким образом, что расстояние от произвольной точки М_А на поверхности s ₄ до точки ^s на поверхности ^ M составляет r_A .

• 1.    Задача определения уровней ЭМП в точке М_S в соответствии с принципом Гюйгенса-Кирхгофа может быть разделена на две части: вну-

• тренняя задача СТА о возбуждении поверхности сторонними источниками, распределенными в объеме пространства вокруг точки M0; и внешняя задача СТА о расчете уровней электрической Е-составляющей и магнитной Н-составляющей ЭМП в точке МS на заданной поверхности ^м.

• 2.    Внутреннюю задачу СТА отличает неопределенность исходных условий, которая не дает возможности убедительно описать источники на S_A ни в детерминированном, ни в стохастическом виде: мы действительно «просто не знаем», но как «практические люди» предполагаем, что в рамках метода СИМ неравномерное по интенсивности и временным сдвигам возбуждение S 4 можно задать путем введения амплитудных и временных ошибок, а режим работы АСА – считать гармоническим с круговой частотой ω .

• 3.    Также в рамках метода СИМ, который требует применения максимально простых и «прозрачных» ММ, будем считать, что временные ошибки (в гармоническом режиме – это фазовые ошибки) можно определить с помощью метода геометрической оптики, рассматривая набеги по фазе лучей, приходящих в точки поверхности S от разных точек M ₀ внутри подлежащего защите помещения (ПЗП), в пределах которого распределены сторонние источники ЭМП (ЭВМ, аппаратура связи, информационное оборудование и т.п.).

• 4.    Неравномерность возбуждения АСА по интенсивности ЭМП определяется двумя факторами: затенением aS элементами инфраструктуры

• 5.    Уточнить значения М<у„) на конкретных частотах CD „ можно с помощью натурного моделирования – путем проведения эксперимента в ПЗП, однако определить значения А*,) аналогичным образом нельзя. Поэтому разработчику СИМ-модели следует, располагая сведениями о размерах ПЗП и местах расположения сторонних источников ЭМП с частотой (О„, оценить возможные набеги по фазе А^К) для разных точек АСА, размещенной на поверхности ^А ^? чтобы ограничиться этим при проведении СИМ.

• 6.    Дискретизированные энергетические спектры сигнала GcW и помехи Gn^_nY где n [1; N ], дают возможность определить частотную характеристику критерия эффективности САЗ СА – отношения «помеха/сигнал» %Vo_n) = G₁AcoAIGAco„^ чтобы сравнить полученные значения с нормативом Zo • при всех Z(

• 7.    На каждой частоте CD „ уровни G_c^„) и определяются в одинаковых условиях и по одной и той же методике [11], поэтому достоверность и точность полученных относительных значений

  

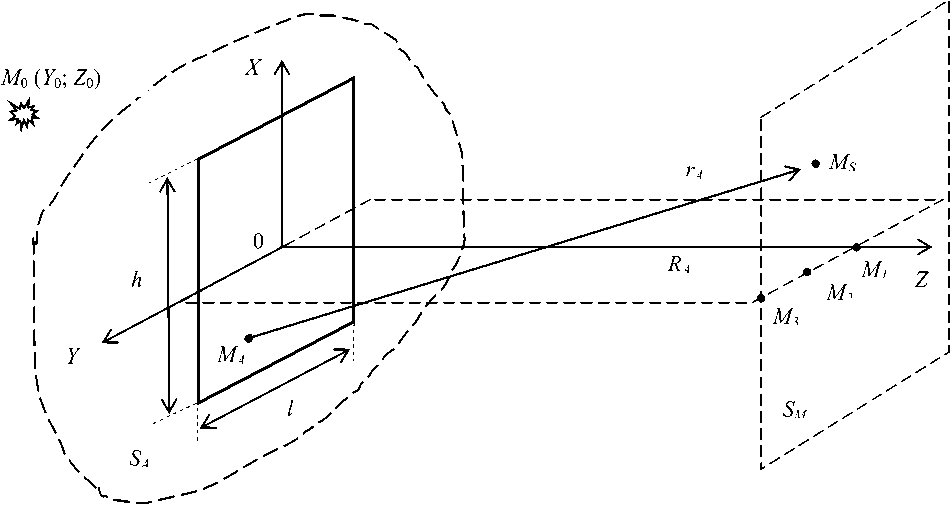
  Рис. 3. Расположение АСА в декартовой системе координат и схема лабораторного эксперимента [12; 22]

  
  

• 8.    После оценки с помощью методов сценариев и функционально-стоимостного анализа всех возможных вариантов реализации САЗ осуществляется выбор наилучшего из них – с учетом субъективных мнений и предпочтений специалистов, а также на основании объективных данных, полученных методом СИМ, что обеспечивает комплексное решение поставленной задачи: проектирование САЗ СА с требуемыми характеристиками эффективности.

(оборудование, персонал, мебель) и ЭМП стоячей волны, возникающей в ПЗП, поэтому амплитудные ошибки, которые также зависят от частоты, могут быть существенными в пределах М(со) [0; 1]. Аналогичным образом фазовые ошибки ^

[0; Лр^], причем с ростом ω значение A?W -±180".

z(a„) будет существенно выше, чем у абсолютных исходных данных, найденных с оговоренной неопределенностью, – таким образом, замена в рамках ОМС верифицированных знаний о параметрах и условиях работы элементов САЗ аксиологическими знаниями специалистов СИМ способствует достижению поставленной цели: анализу эффективности каждого рассматриваемого варианта реализации САЗ СА.

Приведенный пример демонстрирует возможности эвристического подхода к проведению СИМ по МДМ совместно с другими методами моделирования СА.

СИМ по МДМ и технология ММК

Кратко остановимся на отличиях СИМ от ММК, который известен с 1949 г., когда Н. Ме-трополис и С. Улам впервые изложили его сущность [23]. Название метода связано, как известно, с игрой в рулетку, которая, с точки зрения теории СИМ, является простейшим устройством для разыгрывания (получения последовательностей) случайных чисел (СЧ), на использовании которых базируется ММК. С развитием компьютерных технологий была удобно для пользователей решена задача разыгрывания так называемых псевдослучайных чисел, – которые при проведении СИМ используются как СЧ (отметим, что в [3-5; 11-12 и др.] используется более совершенная процедура разыгрывания СЧ).

Этим обстоятельством во многом обусловлено нынешнее широкое применение метода СИМ в качестве универсальной и эффективной информационной технологии – обычно в интересах исследования наиболее сложных (технических, экономических, экологических и т.п.) СС – с учетом непредсказуемых (случайных) факторов, обычно отрицательно влияющих на эффективность их функционирования.

Поскольку ММК требует проведения большого числа испытаний, его часто называют методом статистических испытаний, а так как в настоящее время эти испытания обычно проводятся с применением ЭВМ, – еще и методом статистическо- го компьютерного моделирования (который следует отличать от метода СИМ).

Методика СИМ предусматривает последовательное проведение следующих действий.

Этап 1. Определение состава исходных данных (детерминированных и случайных, входных, внутренних и внешних), оказывающих влияние на процесс функционирования СС как объекта СИМ; а также выходных характеристик (результатов СИМ) и критериев для оценки путем анализа этих характеристик (результатов) эффективности функционирования СС.

Этап 2. Проведение комплексного (в том числе статистического) исследования СС, которое включает сбор и обработку информации о ней с целью выявления законов распределения исходных данных, – при этом реальные данные могут быть использованы как для определения используемых теоретических законов, так и для получения эмпирических распределений, из которых можно выбрать исходные данные, необходимые для моделирования СС.

Этап 3. Идентификация типов законов распределения исходных данных и расчет статистических оценок параметров этих законов – обычно с применением пакетов программ прикладной статистики, которые обеспечивают работу в диалоговом режиме без специальной подготовки пользователей.

Этап 4. Разработка ММ, которая производится сначала для каждого блока СС, а затем для СС в целом, – с последующим программированием данной модели на ЭВМ и разработкой плана компьютерного эксперимента для имитации процесса функционирования СС.

Этап 5. Имитация процесса функционирования СС на модели, реализованной в виде пакета прикладных программ, производимая в диалоговом режиме, с возможностью вывода и проверки после каждого цикла моделирования промежуточных данных, необходимых для формирования результатов СИМ.

Этап 6. Завершение эксперимента при достижении заданной доверительной вероятности (надежности) или заданного числа реализаций СИМ-модели – с выводом на печать результатов СИМ, представляющих собой массивы выходных расчетных данных, которые обычно подлежат статистической обработке для удобства последующей интерпретации пользователем.

Мы видим, что идеология СИМ (как в общем виде, так и в частном случае: при использовании версии МДМ) гораздо шире идеи использовать ММК в его современном компьютерном вариан- те. Уникальным достоинством метода СИМ при исследовании СА [3] представляется возможность воспроизводить поведение СС путем реализации динамических моделей: например, для анализа поляризационных эффектов, сопровождающих процесс излучения АСА, а также игры с противоположными интересами при моделировании систем защиты информации [14-15].

Заключение

Рассмотренные в статье отличия от теории АФУ и СТА, а также от других близких разделов теоретической радиотехники и теории компьютерного моделирования позволяют считать теорию СА одним из направлений развития СТА – в необходимой и достаточной мере самостоятельным, а также актуальным по области применения. Наряду с традиционными методами и средствами моделирования: математического, физического, эвристического, вербального и т.п. основным инструментом теории СА является компьютерное имитационное моделирование – в виде СИМ по МДМ с использованием компьютерной технологии ММК.

Самостоятельный интерес представляет проблема преодоления неопределенности знаний об СА с помощью СИМ по МДМ [13]. Наиболее очевидный практический выход результатов теории СА в настоящее время связан с разработкой низкоэнергетических систем активной защиты конфиденциальной информации. Автор выражает признательность участникам Международной конференции «Параллельная компьютерная алгебра и ее приложения в новых инфокоммуникаци-онных системах» (Северо-Кавказский Федеральный университет, г. Ставрополь, октябрь, 2014) за обсуждение тематики данной статьи.