Теория сред с сохраняющимися дислокациями: общая и прикладная теория межфазного слоя

L «            »                      -[1‒5]:

1 СГС 11

LA — J 11

L A 2 C ijnm

5 Ri J Rn 2C12  Ri x2Cijnm    dnm

jсxm         сxj

+C  dd“ + 33

ijnm ij nm ijnm nm ij

dV,

Cijnm ^ pq 6 ij 5 nm +(ц pq +Х pq )6in 5 jm +(ц pq -х pq )8im 5jn.

TWPI                                    ₀     R _i

Ri ‒ вектор перемещении, dij ‒                          - с xj сии, dij ‒ тензор свободной дисторсии, ij ‒ тензор дислокаций Де Вита, Cijnm ‒ тензоры модулей дефектной среды . Введем тензор дислокационной поврежденности tij, такой, что ij ia aj, ij = Э din -Э nmj = Э tia -эnmjda0 „ + tia а dan -Эnmj =аtip -Э    0         0 (2)

ij nmj nmj an ia nmj qbj pq ijpq pq .

о xm       о xm            с xm       с xb

Подставляя (2) в лагранжиан (1), получим

LA ¹№ ^C

2 ijnm

Ri Rn dV xj xm

C     C11 „ + 2C12 t + C22 t t+ ijnm ijnm ijqm qn pjqm pi qn abcd abij cdnm .

В результате модель сред с сохраняющимися дислокациями (1) приведена к виду модели классической неоднородной среды (3). В ней тензор модулей Cijnm становится тензорным полем , отличным от по -стоянного поля там, где существенным является вклад составляющих, содержащих tij . Такими областями являются окрестности поверхно-стей, линий и точек возмущения. Эти области можно трактовать как некоторые межфазные слои с переменными по координатам упругими свойствами, что и отражено в структуре тензорного поля Cijnm . Пере-менные по координатам упругие свойства, определяемые концентра-цией сохраняющихся дислокаций, в областях таких межфазных слоев можно описать с помощью двух алгоритмов . Первый: -ной задачи механики сред с сохраняющимися дислокациями (1) с ис- комыми ПОЛЯМИ Ri и dij . Второй:

тензорного поля C ijnm в рамках итерационной процедуры последова ^-тельного интегрирования подсистем уравнений относительно R_i и d_ij .

• 2.    Определение модели поврежденного межфазного слоя

Представим лагранжиан (3) модели эквивалентной неоднородной

:

L A 12 №

Cijnm  1 Cni™dV

ijnm V ijnm

R i R n

x j

xm

Ri Rn xj xm

dV dV 21V ш CijnmdV ш

R i ^R

i n dV . xj xm

:

Eijnm   1- fff CiinmdV,

ijnm V ijnm ,

£-. = ijnm

R i ^R

i n dV . xj xm

Обратим внимание на то, что компоненты тензора эффективных модулей E ijnm , с одной стороны ^, не зависят от координат ^, а с другой стороны, являются функционалами тензорного поля t_ij в соответствии с (3) и (5). Пренебрегая в лагранжиане (4) первым слагаемым потенци-альной энергии, получим лагранжиан теории межфазного слоя

LA1пт E

2 ijnm

R i ^R i n dV

xj xm

Соответствующее уравнение Эйлера выглядит следующим об ■

:

Eijnm 2Rn -+PiV I5 RidV +Я сxjс xm

FR1

X Pi   Eijnm n j   n- 5 RidF  12 еijnmV5Eijnm 0.

с xm         2

Полученное вариационное уравнение распадается на последова - тельность двух краевых задач .

Первая краевая задача

-   J 2Rn ijnm сxjо xm

V                        R

+ PiV бRidV + ф J PiF Eijnmnj   n " Г RidF 0 (7)

J V             с xm сводится к краевой задаче для однородной эффективной среды, если заданы или вычислены эффективные модули Eijnm . Как уже отмена -лось выше, эффективные модули являются функционалами независи-мото тензорного поля tij и определяются из второй краевой задачи.

¹ ijnm С dV =

2 ijnm ijnm

в 2t )

4Л C ijqm ⁵

+ C22 р t   C33— tai

5 t qn dV +

ijnm pjqm ijnm pi abqd ijnm bjg dmf x x

33                         tai abqd8 ijnm Э bjg э dmf я ai n f 8tqndF 0. с xg

:

Ci1j2qm gijnm U1q2n , C2p2jqmg ijnmU ,C    g ijnm э bjg э dmf33

ijqm ijnm qn , pjqm ijnm qnpi , abqd ijnm bjg dmf qnfaig .

Тогда вторая краевая задача принимает следующий окончатель -:

(Л Uij + Uijnmtnm Uijknml I 2tnm 4 tijdV +<яU i3jk3nml nm nk5tijdF 0. (9) сxk с xl )

Эта краевая задача дает возможность определить поврежденность tij и механические и геометрические свойства межфазных слоев по- вреждений, если заданы или вычислены тензоры энергий

12 2233

U ij , U ijnm , U ijknml .

Для изолированного тела, без адгезионных свойств поверхности, краевая задача (9):

U ¹ _j ² + 22

U ij    U ijnm t nm

22 12 t pq     U pqij U ij .

U pqijUijnm pqij ijnm pn qm

Это решение определяет единственный макроэффект в дефект - 11

ных средах ‒ переход от тензора супермодулеи C ijnm к тензору «по-врежденных ^» модулей E ijnm C ijnm :

C     C ¹¹    2 C ¹² U 22 U 12 ₊ C 22 U 22 U 12 U 22 12

ijnm ijnm ijqm qnab ab pjqm picd cd qnab ab .

Межфазные слои повреждений, как области специфических крае-вых эффектов, могут появиться только при формулировке контактных задач.

В соответствии с (9) контактная задача для межфазного слоя принимает вид

I F

ггг    U ¹ _j ² -I-   22

Uij   Uijnmt I

I

аt nm

ijknml

с xl

U ³³ , ° t_nm nm U ijknml

с xk С xl

₊ ггг    U 1 _j 2 -I- 22

U ij    U ijnm t J

II

аt nm

U ijknml II F          ^с x_l

C

* — и-nm i

бtijdV +

„ аt ijknml     -(+nk)5tijdF +

nm

ijknml

с xk с xl

бtijdV +

U i ³ jk ³ nml t ^nm n k    t ij dF 0.

C          с xl

Индекс I относится к первому телу , II ‒ ко второму, IF ‒ к сво-бодной поверхности первого тела, IIF ‒ к свободной поверхности вто-рого, C ‒ к поверхности контакта. Переменные, входящие в подынте-гральные выражения, не снабжены соответствующими индексами, чтобы не загромождать эти выражения. Энергии контакта для первого и второго тела должны быть записаны для разных сторон поверхности контакта . Единичные векторы нормали к ним коллинеарны, но имеют разные знаки. Стороной с положительным направлением выбрана сто-рона поверхности контакта первого тела с нормалью (+nk) , тогда сто-рона поверхности контакта второго тела будет иметь нормаль, проти-воположную по знаку , и обозначена как (—nk) . Пусть tij для каждого тела удовлетворяет «статическим» граничным условиям на свободных от контакта поверхностях. Выбор этих условий обусловлен тем, что нет возможности задавать/управлять поврежденностью поверхности, если поверхности контакта адгезионно пассивны [6]. Поэтому j ^0.

С учетом этого вариационное уравнение для межфазного слоя повреж- денности принимает вид ff 33 1 (Пnm )I     А (тт^ 1 (nnm )П ЯГ/ А и —

J ) \ U ijknml А л ^d( t ij A “I U ijknml )„ л        'j ‘п I n k dF ""

C J ! 1 Xxt      J             /n   Xxt

5 1( t j )i+1( t j )_n + _ 2 '      2       _

C

I ^⁽ t nm A _/r/33 \ ^⁽ t nm Ai I Xx_t    V jkm Ai ax_l

, (тт 33 \ (tnm A ,(tt33   \   (tnm AllJL, A 1—

⁺ I U ijknml),   д     ⁺ l U ijknml Ат   _я ~ ⁽ t ij A ~ ⁽ t ij Al nⁿkFr -0.

x J ! 1   Xxt     x J 711    оxl   J |_22 JI

Если варьируемые величины при переходе через поверхность контакта не имеют скачка, условия контакта имеют вид

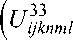
I

setnm )^_U333   \ б(tnm )II xijknml

l Х 711    XX;

0,

⁽ t ij ‘i^_( t ij )II -0.

Вариационное уравнение для (6) распадается на два: вариационное уравнение классической эквивалентной однородной среды с эф -фективным тензором модулей (7) и вариационное уравнение межфазного слоя поврежденности (9). Искомыми функциями в первой из перечисленных моделей являются компоненты вектора перемещений R i , а параметрами - компоненты тензора эффективных модулей E ijnm , являющиеся функционалами компонентов тензора дислокационной по -врежденности t ij . И наоборот, искомыми функциями во второй из перечисленных моделей являются компоненты тензора дислокационной поврежденности t ij , а параметрами - компоненты тензоров энергий U l ^т, U ij ² m , u j _knml , являющиеся функционалами компонентов вектора перемещений R i .

Для эквивалентной среды имеет место теорема Клапейрона

^-№ Eanm^Rn^R-dV = 0 ил и U = A/2. ijnm xm xj

Теорема Клапейрона (11) позволяет из (6), при поле перемеще-НИЙ, удовлетворяющем (7), сформулировать лагранжиан для межфаз-ногослоя, из которого следует вариационное уравнение (9)

L1ПТ E    Rn Ri dV 1E - г V

₂     E ijnm xx ₂ ijnm ijnm

¹ [[[    C i ¹ j ¹ nm _s

₂       C ijnm

+ 2U12t + U22 t t + U 33    tij tnm dV ijnm 2Uij tij    ijnm ij nm ijknml Av. Av.

xk   xl

Заметим ^, что первое слагаемое C ijnm е ijnm в данной постановке можно отбросить, так как при заданных перемещениях вариация этого слагаемого обращается в ноль в силу 5s ijnm 0 .

3. Прикладная теория межфазного слоя

Вариационное уравнение (9) и соответствующий ему лагранжиан (12) приводят в общем случае к системе девяти уравнений второго по - рядка и соответствующей краевой задаче, решение которой является достаточно сложным. Поэтому представляется целесообразным пред-дожить упрощенную, прикладную , модель, содержащую меньшее ко-личество неизвестных и меньшее количество физических параметров .

Первая цель достигается введением векторного потенциала для

:

6t ij xj

.

Лагранжиан (12) при этом принимает вид

LЛ/ Ui1j2njtidF + 12 ш Ui

22 5 t_i 3 t _n 33

ijnm             U ijknml

сxj сxm

82tiа2tn xj xk xm x

dV.

Обозначим U_ij n_j P i . Тогда с точностью до знака лагранжиан (14) будет совпадать с лагранжианом градиентной модели Тупина [2], если трактовать вектор-потенциал t_i как вектор дополнительных пере-мещений в межфазном слое ^, а тензоры энергии U ijnm , U ijknml как соот ^-ветствующие тензоры модулей межфазного слоя.

^L =ч P i^t t i dF ¹₂ ш U ijnm

5ti 5t in

Uijknml оxj о xm

б 2ti 3 2tn J xj xk xm xl

dV . (15)

Специфика данной постановки заключается в том, что и «внеш-няя нагрузка» Pit , и«тензоры модулей » Uijnm , Uijknml межфазного слоя зависят от деформированного состояния тела в целом еijnm (5), а также от физических параметров дефектной среды фазы ‒ тензоров модулей 12     22     33

C ijnm , C ijnm , C ijnm .

Вторая цель достигается введением «гипотезы пропорционально- »               C i ¹ j ² nm , C i ³ jn ³ m              C i ² jn ² m .

12        22

ijnm      ijnm

33      2 22

ijnm ijnm .

Таким образом, физические свойства межфазного слоя для каж-дой фазы определяются пятью параметрами:- тропного тензора Cijnm и введенными параметрами k, h, вместо девя-

‒                                 Ci1j2nm, Ci2jn2m, Ci3jn3m .- зом, показано , что механические свойства межфазного слоя относятся (             Ci1j2nm, Ci2jn2m, Ci3jn3m)- динены. Межфазный слой для каждой фазы является изотропным не-классическим объектом, обладающим неклассическими механически-ми свойствами, которые в общем случае характеризуются девятью па-раметрами, а в приближенном (прикладном) варианте ‒ пятью .