Теория вероятностей и математическая статистика: отличительные особенности

Многие вещи нам не понятны потому, что наши понятия слабы, но потому, что сии вещи не входят в круг наших понятий.

Козьма Прутков

Известно что, примерная программа основного общего образования по математике определяет содержание математического образования применительно к основной школе. Но раздел «Вероятность и статистика» -обязательный компонент школьного образования. Этот материал необходим для формирования у учащихся умения воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты.

Как же связаны между собой теория вероятностей и математическая статистика?

Теория вероятностей изучает объективные закономерности массовых случайных событий и является теоретической базой для математической статистики, занимающейся разработкой методов сбора, описания и обработки результатов наблюдений. Путем наблюдений (испытаний, экспериментов), т.е. опыта в широком смысле слова, происходит познание явлений действительного мира.

Таким образом теория вероятностей изучает математические законы распределения случайных событий, и фактически является теоретической базой для математической статистики. Так в теории вероятностей обычно распределение задано тем или иным образом, и требуется найти вероятности, числовые характеристики (например, математическое ожидание, дисперсию и т.п.), построить графики функции и плотности распределения. А в задачах математической статистики, наоборот, известны данные, собранные по результатам какого-то эксперимента или наблюдения, по которым следует определить закон распределения, наиболее подходящий в данном случае, достоверную с некоторой долей вероятности информацию о том, какими могут быть математическое ожидание или среднеквадратическое отклонение величины и т.п.

Поэтому математическая статистика - это раздел математики, который изучает методы сбора, систематизации, обработки и использования статистических данных для получения научно обоснованных выводов и принятия на их основе решений.

Именно математическая статистика дает методы для обработки данных, алгоритмы для проверки статистических гипотез, критерии адекватности и значимости выбранной модели или закона, обоснованные границы точности для параметров распределения, которые мы можем получить исходя из наших данных и т.п.

Статистические данные по своей сущности зависят от многих случайных факторов, поэтому математическая статистика тесно связана с теорией вероятностей, которая является ее теоретической основой.

Число, являющееся выражением меры объективной возможности наступления события, называется вероятностью этого события и обозначается символом Р(А).

Вероятностью события А называется отношение числа исходов m, благоприятствующих наступлению данного события А , к числу n всех исходов (несовместных, единственно возможных и равновозможных), т.е.

P ( A ) = - .

n

Следовательно, для нахождения вероятности события необходимо, рассмотрев различные исходы испытания, подсчитать все возможные несовместные исходы n, выбрать число интересующих нас исходов m и вычислить отношение m к n .

Из этого определения вытекают следующие свойства:

• 1.    Вероятность любого испытания есть неотрицательное число, не превосходящее единицы. Действительно, число m искомых событий заключено в пределах 0 <  m <  n . Разделив обе части на n , получим

• 2.    Вероятность достоверного события равна единице, т.к. ⁿ и = 1 .

• 3.    Вероятность невозможного события равна нулю, поскольку ⁰ = 0 .

0 <  P ( A ) <  1 .

Рассмотрим решение некоторых задач:

Задача1

Из 20 экзаменационных билетов 3 содержат простые вопросы. Пять студентов по очереди берут билеты. Найти вероятность того, что хотя бы одному из них достанется билет с простыми вопросами.

Решение:

Для начала найдем вероятность того, что ни одному из студентов не достанется билет с простыми вопросами.

Эта вероятность равна

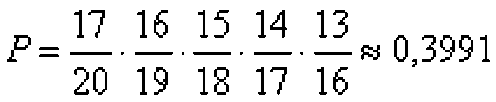
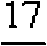
Первая дробь     показывает вероятность того, что первому студенту достался билет со сложными вопросами (их 17 из 20)

Вторая дробь 1 9 показывает вероятность того, что второму студенту достался билет со сложными вопросами (их осталось 16 из 19)

Третья дробь 18 показывает вероятность того, что третьему студенту достался билет со сложными вопросами (их осталось 15 из 18)

И так далее до пятого студента. Вероятности перемножаются т.к. по условию требуется одновременное выполнение этих условий.

Чтобы получить вероятность того, что хотя бы одному из студентов достанется билет с простыми вопросами надо вычесть полученную выше вероятность из единицы.

1-0,3991= 0,6009

Ответ: 0,6009.

Задача2

Имеется 100 одинаковых деталей, среди которых 3 бракованных.

Найти вероятность того, что взятая наудачу деталь без брака.

Решение. В этой задаче производится испытание – извлекается одна деталь. Число всех исходов испытания равно 100, т. к. может быть взята любая деталь из 100. Эти исходы несовместны, равновозможны, единственно возможны. Таким образом, к = 100. Событие ^ - появилась деталь без брака. Всего в партии 97 деталей без брака, следовательно, число исходов, благоприятных появлению события А равно 97 .

Итак,        Тогда         100

Таким образом, в данной статье была сделана попытка проанализировать отличитильные особенности вероятности от математической статистики.