Теплофизические, диффузионные и сегрегационные процессы в зоне фрикционного контакта

Введение. Выяснение особенностей поведения поверхностных слоев, как металлического, так и металлопо-лимерного трибоконтакта — одна из центральных задач в триботехнике. Поэтому для процессов, происходящих в местах контактирования металлополимерных сопряжений необходимо разработать не только методы диагностики, но и более полные теоретические модели, специфическое назначение которых, с одной стороны — учитывать изменения, происходящие в объеме и в пограничном слое, а с другой — приводить к простым инженерным расчетам.

Поэтому на первом этапе наших исследований была разработана методика расчета температурного поля — температуры и температурного градиента в поверхностных слоях фрикционного сопряжения. Установление теоретических представлений о механизме возникновения температурного градиента дает возможность выяснить закономер-

*

∗∗

ности его влияния на трибоэлектрические, диффузионные и сегрегационные процессы, протекающие на фрикционном контакте.

Желание определить температурное поле в поверхностных слоях трибоконтакта классическим методом приводит к необходимости решения краевых сингулярно возмущенных задач — задач с малым параметром при старшей производной [1]. Для асимптотического решения сингулярно возмущенных задач обычно используют метод Вишика-Люстерника или методы сращиваемых многомасштабных разложений [2]. Авторами для нахождения температурного поля в погранслоях трибосистемы применен метод регуляризации сингулярно возмущенных задач, разработанный С.А. Ломовым [3]. Этот метод, объединяющий в себе идеи двух вышеназванных методов, обладает рядом преимуществ по сравнению с каждым из них в отдельности и является, естественно, более прогрессивным. Суть его — в регуляризации сингулярно возмущенных задач с помощью перехода в пространство безрезонансных решений, которое индуцируется исходной задачей. Это индуцированное пространство определяется по спектральным характеристикам исходного оператора, что дает возможность использовать спектральную теорию операторов. Сингулярность исходной задачи влечет за собой появление ненулевого ядра у главного оператора индуцированной задачи.

Расчет температурного поля. В настоящее время установилась единая точка зрения, что определяющим фактором эксплуатационного режима металлического и металлополимерного сопряжения является тепловая напря- женность в узле трения.

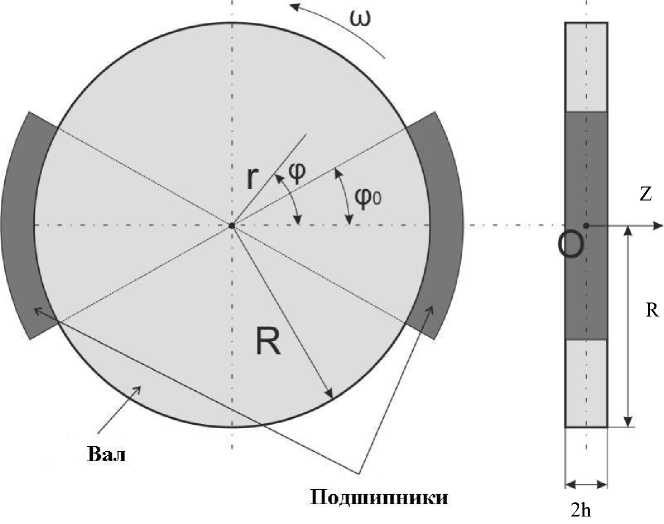
Расчет температурного поля проведен для конкретного сопряжения — колесно-тормозной колодки подвижного состава как наиболее характерной и широко распространенной трибосистемы "вал-частичный подшипник" (рис. 1).

Будем считать, что колесо представляет собой диск радиуса R и толщины 2h (рис. 1). Введем цилиндрическую систему координат ( r, ф, z ) и обозначим через Т (г, ф, z, t) температуру в точке колеса с координатами (г, ф, z) в момент времени t Рассмотрим случай установившегося процесса: колесо вращается с постоянной угловой скоростью ю и сила прижатия колодок к колесу в процессе торможения не меняется. При этих допущениях функция Т ( r, ф, z, t ) является периодической по времени с периодом п/ю (две колодки). Можно считать, что колесо неподвижно, а колодки вращаются вокруг него с той же скоростью ю против часовой стрелки. Оставаясь в рамках основных принципов, сформулированных к настоящему времени исследователями в области термического трибоконтакта, источником тепла будем считать тончайшие непрерывные поверхностные слои, непосредственно примыкающие к фактической площади контакта каждого из трущихся тел, образующие как бы одну систему.

Вал

Подшипники

Z

R

2h

Рис. 1. Схема металлополимерной трибосистемы" вал-частичный подшипник"

При этих допущениях и условии изотропности материала колеса уравнение теплопроводности будет иметь вид:

1 д ( д T )   1 д ² T   д ² T  C • р д T

--I r — I +       +    —-- , r д r ( д r ) r ² дф ²    д z ²     X  д t

Машиностроение и машиноведение

где С — удельная теплоемкость материала колеса; X — теплопроводность; р — плотность; С , р и X считаем постоянными.

Перейдем к формулировке граничных условий. На торцах ( z =± h ) происходит свободный теплообмен с коэффициентом теплоотдачи a z

±X — + az(T—Tc) = 0, z = ±h,                                (2)

где T c — температура окружающей среды.

На цилиндрической поверхности ( r = R ) под колодками происходит генерация тепла

X ” = Q, r=R, dz

фе[- ф0 + tot, ф0 + tot ] o[n — ф0 + tot, п + ф0 + tot ]

где Q = k_TPP u K ( к тр — коэффициент трения, Р — удельная нагрузка на колодку, и — линейная скорость вращения колеса, K — коэффициент разделения тепловых потоков).

На остальных участках цилиндрической поверхности осуществляется свободный теплообмен с коэффициентом теплоотдачи a r

5 T

( T — T_c ) = 0 ,

r = R,

^х—⁺ а д r      r

ф^[— ф0 + tot, ф0 + tot ] ^[п — ф0 + tot, n + Ф0 + tot ]

В результате проведенного расчета установлено, что практически сразу после выхода поверхности катания колеса из-под колодки возникает приповерхностный максимум температуры, который постепенно смещается вглубь колеса [4]. Максимальный перепад температуры наблюдается в диапазоне углов от 2п/5 до п/5. При этом максимум находится на расстоянии 200…1000 мкм от поверхности катания.

Диффузионные процессы. Известно, что при трении в результате термомеханической деструкции полимеров в зоне контактирования с металлом выделяются различные по своей природе твердые, жидкие и газообразные продукты, среди которых большое количество водорода. Водород, в свою очередь, адсорбируется и активно поглощается контактирующей поверхностью металла, что ведет к ее разрушению и переносу твердых частиц металла с этой поверхности на более мягкий полимерный материал. Установлено, что способствует этому три фактора — градиент концентрации, градиент механических напряжений и градиент температуры.

Для оценки влияния температурного поля на профиль концентрации водорода рассмотрена однородная металлическая пластина толщиной l, на гранях которой ( Z = 0 и Z = l) поддерживаются постоянными величины температур Т 0 , Т 1 и концентраций n 0 , n 1 . Будем также считать процесс диффузии водорода в пластину установившимся. Тогда задача расчета концентрации водорода является одномерной, стационарной и сводится к решению следующего уравнения (4)

— Ddn dz

— D • n • Q

1 dT kT 2 dz

= g 0,

при граничных условиях

n ( 0)=no,     n ( 1 )⁼ni.

Здесь D — коэффициент диффузии, выраженный формулой E a D = D 0 e ^kT,

где D 0 — коэффициент диффузии при комнатной температуре; Q — теплота переноса; Е_а — энергия активации;

k — постоянная Больцмана; g 0 — поток водорода — величина неизвестная, подлежащая определенно в процессе решения задачи; Т — температура, является функцией от Z .

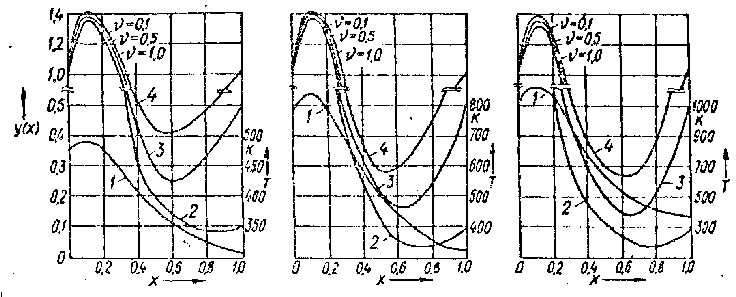
В результате проведенных расчетов установлено, что максимум концентрации водорода практически совпадает с максимумом температуры; величина концентрации в точке максимума не зависит от уровня концентрации и от абсолютной величины температуры на правой нерабочей поверхности образца (при Z = l) (рис. 2).

а)                       б)                           в)

Рис. 2. Изменение концентрации водорода в пластине при Т 0 = 473 К (а); Т 0 = 773 К (б) и Т 0 = 1073 К (в), ν = n 0 /n 1

Для подавления водородного износа в узлах сухого трения разработаны следующие меры [4]:

• 1.    Меры, препятствующие проникновению водорода в металлическое тело;

• 2.    Меры, блокирующие выделение водорода из полимерной композиции;

• 3.    Меры, приводящие к связыванию водорода в прочные химические соединения.

Введением в колесную сталь хрома, ванадия, никеля снижается концентрация биографического водорода, а добавлением в композицию структурирующих агентов достигается невозможность выделения водорода из самой композиции. Введение во фрикционные пластмассы закиси меди, фтористого кальция приводит к уменьшению потока водорода в стальное контртело путем связывания водорода в зоне трения.

Перечисленные меры отодвигают границу катастрофического водородного разрушения сопряженных с пластмассой или смазкой металлических поверхностей.

Сегрегационные процессы. Другим фундаментальным процессом на трибоконтакте, помимо диффузии, является сегрегация, определяющая кинетику и механизм поверхностных явлений на микроуровне [5–11].

С помощью квантовой химии изучены типы химических соединений, возникновение и изменение химических связей на поверхности трущихся тел и на этой основе детально описано поведение материалов на атомном уровне в различных условиях трения. Как показали наши исследования, речь идет, в первую очередь, о явлении зернограничной сегрегации, в результате которой атомы примесных и легирующих элементов выходят на границы зерен, и последствиях этого явления, что впервые предпринималось в трибологии.

Зернограничная сегрегация (ЗГС) — это явление, присущее твердым многокомпонентным материалам, состоящим из микрокристаллитов (зерен). Оно заключается в том, что атомы некоторых элементов, растворенных в объеме зерен, с течением времени выходят на поверхность зерен (т.е. на их границу).

Перестройка структуры границы зерен влияет на термодинамические, кинетические, механические свойства поликристаллических материалов. Как правило, граница зерен является наименее прочной частью зерен. Поэтому состояние границы и явления, связанные с ЗГС, играют существенную роль в процессах разрушения. Из сказанного выше вытекает, что износостойкость стали и других поликристаллических материалов во многом определяется свойствами границ между зернами поверхностных слоев. Хотя эти слои по структуре зерен могут существенно отличаться от внутренних областей поликристаллов, механизмы разрушения поверхности и внутренних областей имеют много общего.

Существуют различные точки зрения на то, каким образом сегрегированные атомы способствуют разрушению. Одна из гипотез базируется на том, что в процессе зернограничной сегрегации связь металл-металл заменяется на более слабую или более сильную связь металл-сегрегированный атом. Этот факт дает основание полагать, что величина энергии связи атомов во многом определяет способность сегрегированных атомов ослаблять или упрочнять границы зерен.

Появившиеся в последние десятилетия методы квантово-химических расчетов, основанные на приближении теории функционала плотности (DFT), позволяют провести анализ атомных взаимодействий, влияющих на разрушение металлов. Взаимодействие атомов на границах зерен и его влияние на износостойкость поверхностных слоев ста-

Машиностроение и машиноведение

ли изучались нами с помощью пакета программ ADF, основанного на приближении DFT. Этот пакет дает возможность рассматривать соединения переходных металлов, включающие сотни атомов, что важно для применений в случае стали.

Взаимодействия между зернами при наличии сегрегированных атомов исследовалось с помощью двух моделей — модели многоатомного кластера и модели двупериодической пластины. Совпадение результатов, получаемых в рамках этих двух существенно различающихся моделей, свидетельствует о точности результатов.

Цель проводимого анализа — убедиться, что появление сегрегированных атомов на межкристаллитных границах является не сопутствующим эффектом, а одной из основных причин ослабления прочности связи между кристаллитами и последующего за этим разрушения поверхностного слоя металла.

Многоатомный кластер, имитирующий сегрегацию в поликристаллическом материале, должен, очевидно, содержать некоторое количество атомов матрицы (из прилегающих слоев двух соседних зерен), а также сегрегированных или продиффундировавших атомов, расположенных на границе. Размер кластера должен быть достаточно большим, чтобы с его помощью возможно точнее воспроизводились основные качественные и количественные закономерности сегрегации. Однако практика квантово-химических расчетов показывает, что во многих случаях кластеры сравнительно малых размеров на качественном и полуколичественном уровнях могут воспроизводить особенности изучаемого явления.

При моделировании условий, при которых происходит сегрегация, использовали тот известный факт, что на наиболее узком участке границы между зернами в поликристалле (т.е. в месте контакта зерен) ширина границы составляет величину порядка постоянной решетки. Это позволило рассмотреть следующую простую модель границы (рис. 3а): в многоатомном кластере железа (на рисунке изображен 30-атомный кластер) атомы из среднего слоя заменены сегрегированными атомами. При этом два верхних и два нижних слоя имитируют соответственно верхнее и нижнее зерна поликристалла, а средний слой представляет собой границу между зернами. Будем называть такой кластер сегрегационным. Кластер, который содержит только атомы Fe , моделирует чистый металл.

Безусловно, такая модель не учитывает всего разнообразия условий, важных для процесса сегрегации и проблемы износостойкости (к таким условиям можно отнести наличие неоднородностей на поверхностях кристаллитов, непараллельность поверхностей, наличие дислокаций и многое другое). Основное назначение предлагаемой модели — во-первых, оценить влияние ближайшего атомного окружения на химическую связь между сегрегированными атомами и атомами матрицы в месте контакта зерен, и, во-вторых, изучить, как эта связь влияет на прочность микроскопических областей и поверхностных слоев поликристалла.

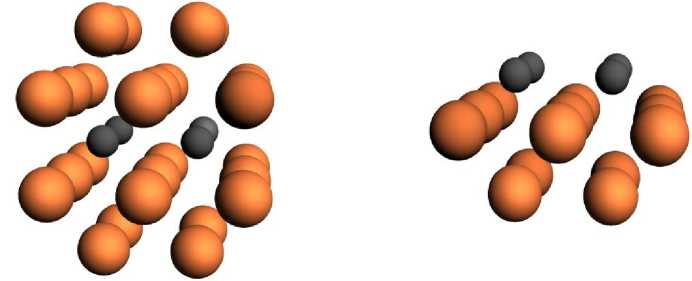
Если в этой модели убрать атомы двух верхних слоев (рис. 3б), то оставшиеся атомы (нижние слои + слой примесных атомов) имитируют явление адсорбции на поверхности железа с индексом Миллера (100). Такой кластер будем называть адсорбционным.

а)                                                         б)

Рис. 3. Кластеры железа с сегрегированными атомами (а) и адсорбированными атомами (б).

Крупные кружки соответствуют атомам Fe, мелкие — сегрегированным атомам

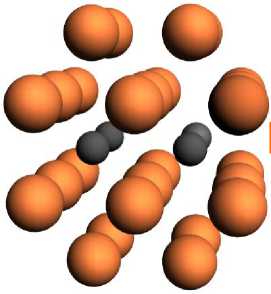
В соответствии с экспериментальными данными о характере разрушения границы предполагалось, что модельная система (сегрегационный кластер рис. 4а) в результате силового воздействия может распадаться на две части (рис. 4). Одна из них состоит из атомов только одного зерна (кластер из чистого железа рис. 4б), а другая — из атомов другого зерна и слоя сегрегированных атомов (адсорбционный кластер рис. 4в).

а)

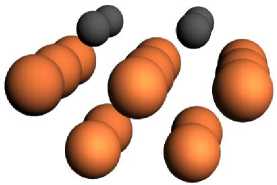
в)

Рис. 4. Распад сегрегационного кластера на кластер из чистого железа и адсорбционный кластер: а — кластер железа с сегрегированными атомами; б — кластер из чистого железа; в — кластер железа с адсорбированными атомами

Нами проводились расчеты для кластеров, состоящих из 18 и 30 атомов. В качестве рассчитываемых характеристик были выбраны энергия связи E св кластера и межатомные расстояния. Полученная с помощью пакета ADF энергия связи кластера, взятая по модулю, приближенно представляет собой энергию, которую нужно затратить для разрыва всех связей в кластере. Как известно, результаты расчётов энергии сильно зависят от выбранного приближения. Поэтому вычисления для всех исследованных объектов проводились единообразно. В расчётах применялся базис TZ2P и использовались “замороженные” остовные орбитали. Для проверки чувствительности расчётов к методу вычисления энергии применялись две разные схемы. Для 18-атомных кластеров использовалось приближение LDA (приближение локальной плотности), а для 30-атомных — нелокальное приближение GGA BLYP.

Были проведены расчеты энергии связи E св кластеров, которые содержат адсорбированные и сегрегированные атомы всех химических элементов из четырех периодов таблицы Менделеева, с порядковыми номерами от 1 до 36 (от водорода до криптона). Эти дополнительные атомы размещались либо на внешней поверхности кластера (в случае адсорбции), либо в среднем слое (в случае сегрегации). В обоих случаях рассматривалось положение дополнительных атомов над центрами квадратов из атомов железа (позиция fourfold) или над сторонами этих квадратов (позиция twofold).

Зная энергии связи адсорбционных и сегрегационных кластеров, можно рассчитать энергию E d , необходимую для разрыва (распада) кластера с образованием двух частей, имитирующих зерна в модельном кластере. Ее значения определяются по формуле:

E d =|E s – E g – E a | , (1)

где E s — энергия связи сегрегационного кластера, содержащего два зерна и граничный слой между ними, E g — энергия связи кластера, состоящего из одного зерна, E a — энергия связи адсорбционного кластера, состоящего из зерна и граничного слоя. По этой же формуле можно рассчитать и энергию разрыва кластера из чистого железа, полагая, что 30-атомный кластер Fe 13 Fe 4 Fe 13 делится на фрагменты Fe 13 Fe 4 и Fe 13 .

Машиностроение и машиноведение

Таблица 1

Энергия распада (в эВ) сегрегационных кластеров Fe 13 X 4 Fe 13 (X = H, …, Kr)

			I	II	V	VI	VII	VIII	0
1	H 3,3								He 0
2	Li 3,1	Be 8,4	B 9,4	C 7,0	N 5,4	O 2,1	F		Ne 0
3	Na 3,0	Mg 4,8	Al 6,4	Si 6,0	P 4,8	S 1,9	Cl		Ar 0
4	K 1,8	Ca 3,7	Sc 4,5	Ti 8,5	V 9,4	Cr 11,2	Mn 8,8	Fe     Co        Ni 10,4     10,3          8.2
	Cu 6,3	Zn 5,4	Ga 5,1	Ge 4,6	As 3,2	Se 2,1	Br		Kr 0

Табл. 1 фактически отражает совместимость различных элементов с железом на его зернограничных поверхностях. Для элементов начала периода их связь с железом слабая (по сравнению со связью Fe–Fe), но с ростом номера элемента она вначале увеличивается, а затем во второй половине периода уменьшается. При перемещении вдоль группы связь, как правило, ослабевает. Это означает, что свойства химической связи различных элементов с железом находятся в периодической зависимости от заряда ядра атомов, что соответствует периодическому закону Д.И. Менделеева.

На рис. 5 данные из табл. 1 для большей наглядности представлены в графической форме. Здесь же для сравнения приведены результаты расчёта для 18-атомных кластеров, для которых использовалось приближение LDA. Наиболее существенный вывод, вытекающий из сравнения двух кривых на рис. 5, состоит в том, что обе кривые в значительной степени подобны. Чётко видна однотипная периодическая зависимость энергии распада кластеров от порядкового номера элементов.

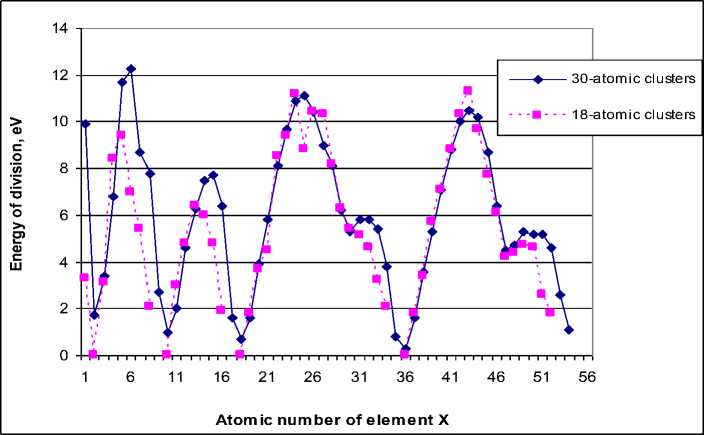
Рис. 5. Зависимость энергии распада Ed многоатомных кластеров от атомного номера элемента Х

Полученные результаты могут служить теоретической базой для прогнозирования прочностных свойств стали с различным составом легирующих и примесных элементов.

Формирование пленки фрикционного переноса . Что касается антифрикционных материалов, то с позиций структурной самоорганизации, которая в случае металлополимерной трибосистемы проявляется в образовании полимерной пленки фрикционного переноса (ПФП) из продуктов износа, изучен механизм ее образования. Нашими исследованиями показано, что основой кинетического условия самоорганизации является согласованность скоростей образования пленки переноса и ее разрушения.

Так, ПТФЭ и ПЭНД при трении с металлом имеют низкий коэффициент трения за счет способности формировать на контртеле высокоориентированную пленку переноса, но за счет слабой адгезии к металлу пленка и в целом полимерный образец интенсивно изнашиваются. Другие полимеры (ПКА, ЭД-20), наоборот, обладают достаточно сильной адгезией к металлу, но не образуют ориентированной пленки, обеспечивающей малый коэффициент трения.

Для повышения износостойкости пленки фрикционного переноса весьма перспективным является исследование механизма ее формирования на металлическом контртеле. При этом конечным продуктом является создание композита с управляемыми фрикционными характеристиками путем реализации последовательного разделения компонентов смесей полимера. С одной стороны, должна быть обеспечена адгезионная прочность пленки фрикционного переноса, а с другой — формирование тонкой высокоориентированной пленки, обеспечивающей низкий коэффициент трения.

Для исследования кинетики формирования пленки фрикционного переноса (ПФП) были выбраны композиты: фенилон, капрон, ЭД-20 с добавками ПТФЭ и ПЭ, которые подвергались испытанию на торцевой машине трения с металлической пластиной (Сталь 45) при нагрузке Р = 2 МПа и скорости υ = 0,5 м/с.

При исследовании ПФП с помощью рентгеноэлектронной спектроскопии полученные спектры позволили изучить зависимость интенсивности рентгеноэлектронных линий по углероду (С1S), фтору (F1S), кислороду (O1S) от времени фрикционного контактирования. Исходя из анализа зависимости интенсивности этих линий можно выделить следующие этапы формирования пленки фрикционного переноса. Первый этап охватывает промежуток времени до 1 минуты для капрона, 1,5 минуты для ЭД-20 и 2 минуты для фенилона от начала эксперимента. В этот период поверхностный слой ПФП формируется в основном за счет продуктов переноса связующего. Это следует из увеличения интенсивности рентгеноэлектронных линий C1S и O1S, характерных для связующего, и, одновременно, уменьшения интенсивности линий F1S и C1S, относящихся к ПТФЭ и ПЭ. Второй этап относится к периоду времени от 1 до 6 минут для капрона, от 1 до 15 минут для фенилона и от 1 до 20 минут для ЭД-20. В этот период содержание продуктов фрикционного переноса ПТФЭ или ПЭ на поверхности металлического контртела увеличивается, а ПФП связующего одновременно уменьшается. Третий этап охватывает интервал времени от 10 до 40 минут для капрона, от 20 до 50 минут для фенилона и от 30 до 60 минут для ЭД-20. В пределах этого промежутка времени количество продуктов фрикционного переноса ПТФЭ или ПЭ уменьшается, а связующего увеличивается. Последующие трехпериодные стадии формирования пленок переноса имеют такой же характер образования, но интервал второго периода — образование пленки ПТФЭ или ПЭ для всех связующих значительно дольше (до 60 минут).

Заключение. Расчеты тепловой задачи показывают, что максимальное значение температуры в стальном образце металлополимерного сопряжения достигается не на поверхности, а в подповерхностном слое. Это влияет на диффузионные процессы в металлополимерной трибосистеме. Показано, что сегрегированные атомы могут, как ослаблять, так и упрочнять границы зерен. Исследован механизм образования пленки фрикционного переноса и показано, что она является основой кинетического условия самоорганизации.