Теплофизическое моделирование процесса нанесения внутритрубного покрытия методом центробежного СВС

Способ получения композиционных слоистых металлокерамических труб с внешним металлическим и внутренним керамическим слоями с помощью реакций самораспространяющегося высокотемпературного синтеза (СВС) разработан в 70-х годах прошлого века. Основоположниками этого направления стали классики применения метода СВС: Osamu Odawara (Япония) и А.Г. Мержанов с сотрудниками (СССР).

Стальные композиционные трубы, покрытые внутренним слоем металлокерамики, используются для транспортировки абразивных материалов в угольной и металлургической промышленности, теплоэнергетике и т. п., поскольку обладают устойчивостью к эрозии, коррозии, механическому износу, нагреву [1–3].

Чтобы с помощью метода центробежного СВС получить покрытие, удовлетворяющее эксплуатационным требованиям, необходимо обеспечить оптимальные условия его синтеза. Поэтому возникает необходимость создания математической модели процесса нанесения внутритрубного покрытия методом центробежного СВС, которая бы учитывала все множество теплофизических и физико-химических параметров, формирующих это покрытие.

В работе [4] при создании математической модели было принято, что теплообмен происходит только радиально, и не учитывалась скорость фронта волны горения, от которого во многом зависят условия протекания процесса. Задачей настоящего исследования стала разработка математической модели центробежного СВС, учитывающей теплофизические факторы процесса, в том числе скорость распространения фронта горения.

В процессе формирования покрытия методом центробежного СВС по длине трубы образуется три области: сухой смеси, жидкой и твердой фаз покрытия. В общем виде математическая модель распределения температур в ходе центробежного СВС должна учитывать теплообмен между среда- ми: порошкообразной смесью для СВС; твердой фазой, образующей покрытие; жидкой фазой, металлом стенки трубы, а также газовой фазой внутри трубы и снаружи.

В настоящей работе представлена методика, использовавшаяся для моделирования теплообмена между стенкой трубы и смесью для СВС в процессе прохождения фронта горения вдоль трубы [5, 6].

При составлении математического описания процесса теплообмена сделаны следующие допущения: толщина слоя смеси СВС постоянна по радиусу и по длине трубы, теплофизические пара- метры сред постоянны и не зависят от температуры, фронт волны горения распространяется в режиме устойчивого, стационарного горения (в поршневом режиме).

С учетом принятых допущений уравнения энергии для стенки трубы и смеси, начальные и граничные условия примут вид:

<

^^ = 7     -T ) + dt     XCT,S 1 ( S 1 ст )

+ Y (T -T } + a ^{д Т}'^{1 х} ст,см V см ст / a ст _ 2 ^;

dX ат ат см         см д + Ur Д = Хсм,ст (Тст Тсм) + д t         дx,

+ V             А +а д Тсм +__Q■

+ хсм, s 2 (Ts 2   тсм ) + a см _ 2 '

’                       d X ²     С см Р см

^Т ст ⁽ x , 0) = Ф ст ⁽ x ), ^Т см ⁽ x , 0) = Ф см ⁽ x );

Т ст (0, t ) = Ф ст ( t ), Т см (0, t ) =ф см ( t);

^ Хст етст^0,!) = аст  (Тст(0,t)-Тсм(0,t));(3)

a x

^ см ^{д Т} см⁽⁰² ^ ⁾- = « см,ст ( Т см (0, t ) - Т ст (0, t )),

I          дx’ где Tст , Tсм , Ts1 , Ts2 – температуры стенки, смеси, окружающей среды снаружи и внутри трубы соответственно;

_ ^а ст, s 1 p ст, s 1            _ ^а ст,см p ст,см

Х ст, s 1 =          Z ; Х ст,см =          Z ;

^р ст ^С ст S ст                 ^р ст c ст S ст

_ ^а см, s 2 p см, s 2 _         _ ^а см,ст p см,ст

Х см, s 2 =           Z ; Х см,ст =           Z ;

рсм c см S см             рсм Ссм S см aст, aсм – температуропроводности стенки, смеси;

U r - скорость продвижения фронта горения;

^а ст, s 1 , ^а ст,см , ^а см, s 2 , ^а см,ст ^- коэффициенты теплоотдачи от стенки к внешней окружающей среде, от стенки к смеси, от смеси к внутренней окружающей среде, от смеси к стенке;

p ст, s 1 , p ст,см , p см, s 2 , p см,ст – периметры раздела между стенкой и внешней окружающей средой, между стенкой и смесью, между смесью и внутренней окружающей средой, между смесью и стенкой;

р _ст, р _см - плотности стенки, смеси;

c _ст, c _см – удельные теплоемкости стенки, смеси;

S _ст, S _см – площади поперечного сечения стенки трубы и смеси;

Q – мощность источника энергии;

Х _ст, Х _см - теплопроводность стенки трубы, смеси.

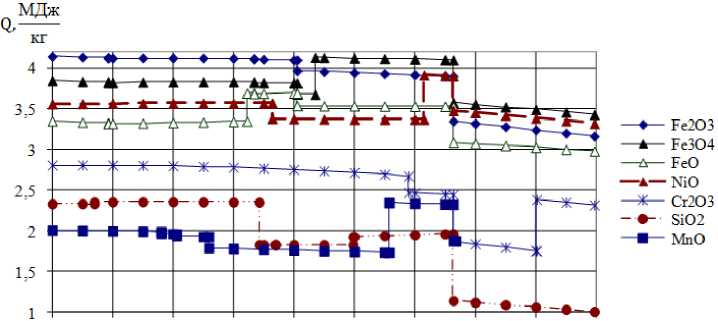
Точный расчет количества теплоты, выделяющейся в процессе СВС, достаточно сложен, так как количество выделяющейся теплоты будет существенно зависеть от температуры протекающего процесса. Представление о характере и количественных характеристиках измерений, происходящих с величиной теплового эффекта в ходе повышения температуры процесса, дает информация, представленная на рис. 1, которая получена с помощью баз данных FactSage, представленных в открытом доступе .

Упрощенно можно рассчитать тепловой эффект реакции как сумму средневзвешенных значений тепловых эффектов реакций алюминия с оксидами в составе смеси.

Для численного решения краевой задачи (1)–(3) использовали метод конечных разностей. Систему (1), условия (2), (3) представили в дискретном блочно-матричном виде:

Т П ^{+ 1} = MT m + NT_S + Q s + 1 ,              (4)

где T m ^{+ 1}, M , T m , N , T_S , Q , I - блочные матрицы вида:

Г0

n + 1 "

F

G

0 "

0

n + 1 2

A

F

C

0

rp n + 1 Tm

=

, M

=

0

n + 1 m - 1

0

A

F

C

.0

n + 1 m

_

L 0

G

F

Г

0 1 n

Г E

0

"

0 2

0

E

0

n T m =

,

N =

=

,

0 n v m

1

0

E

0

0 n L m

J

. 0

E

.

Г0

S "

Гф"

Г 1 1 "

0

S

0

0

T s =

,

Q s =

,

I

=

:

.

0

S

0

0

.0

S _

L

0

. 1 2 _

Элементы блочных матриц – матрицы коэффициентов 0 m , 0 m ⁺¹, A , G , E , F , C , V , 0 s , 1 1 , I ₂ имеют следующий вид:

n

m

n стm n смm

, 0

n + 1

m

n + 1 ст m

n + 1 см m

, 0 S =

T s 1

L T s 2 J

1000   1200  1400   1600   1800  2000  2200  2400  2600  2800 T, К

Рис. 1. Зависимость количества теплоты, выделяющейся в ходе реакции алюмотерми-ческого восстановления из одного килограмма стехиометрических смесей на основе различных оксидов, от температуры процесса

A =

^Т a ст h ²

^Т a см +TU r h ² 2 h

' ^Т Х ст, 5 1    ^ТХ ст,СМ

E =

^ТХ ст, 5 1

^ТХ см, 5 2

I 2 =

Тaст «ст,™ / _ n _ n стm    смm h ^ст   V

h ^а см,ст f ^{Т а} см    ^Ти г )

I+"'

n стm

F =

2т а ст h ²

^ТХ ст,см

¥ =

C =

1 1 =

^ТХ см,ст

Q _,

^Т a ст h ²

G =

h ²

¹ Чем, 5 2 Чем, ст

Т a см   Тиг h2    2h

^{2 т а} см h ² _

^{2 т} a см h ²

^{ст ст,см} (@ ”  @ n

⁽^ ^ст1    ^ ^с м| )

h ^а см,ст f ^т а см   ТЦ ) n

1,2             1 1 ^ см1

^ см I h ^{2    2} h Г

- ®стП )

Для адаптации математической модели использовали интервальный метод для определения параметра c см .

Построенная модель теплообмена между смесью для СВС и стенкой трубы реализована в виде программы для ЭВМ, написанной на языке программирования C# с использованием возможностей параллельного программирования. Программа позволяет рассчитывать распределение температур сред, контактирующих в ходе процесса СВС по длине трубы, в зависимости от времени, прошедшего с момента начала процесса (примеры результатов таких расчетов, проведенных для условий, представленных в таблице, показаны на рис. 2–4).

В процессе дальнейших работ по созданию полной модели процесса планируется разработать модели других частных процессов теплообмена, реализующихся в процессе СВС, а затем объединить их.

Данные, использованные в процессе расчета

Параметры			Стенка	Смесь СВС
Теплофизические	Плотность, кг/м3		7800	4000
	Теплоемкость, Дж/(кг·К)		500	1000
	Теплопроводность, Вт/(м·К)		47	1,00
	Теплопередача, Вт/(м2·К)	Внешняя среда	1000	10000
		Труба/Смесь	30 000	30 000
Геометрические	Внешний радиус трубы, м		0,15
	Внутренний радиус трубы/внешний радиус смеси, м		0,14	0,14
	Внутренний радиус смеси, м		–	0,09481
	Периметр раздела сред, м	Внешняя среда	0,94248	0,59573
		Труба/Смесь	0,87964	0,87964
	Площадь сечения, м2		0,00911	0,03333
Механические	Скорость горения, мм/с		–	20,0
	Скорость вращения, мм/с		1500	1500

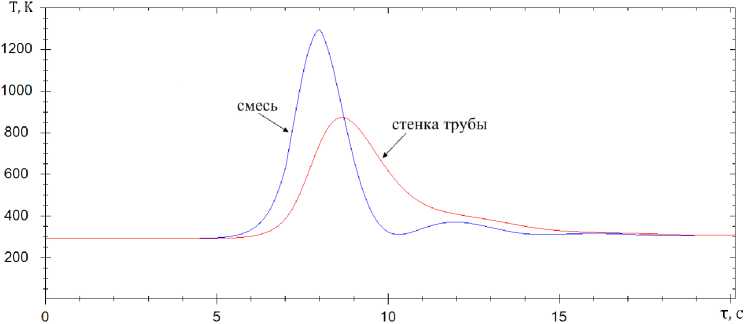
Рис. 2. Пример результатов расчета распределения температур взаимодействующих сред в сечении трубы ( x = 0,15 м) в зависимости от времени, прошедшего от начала процесса

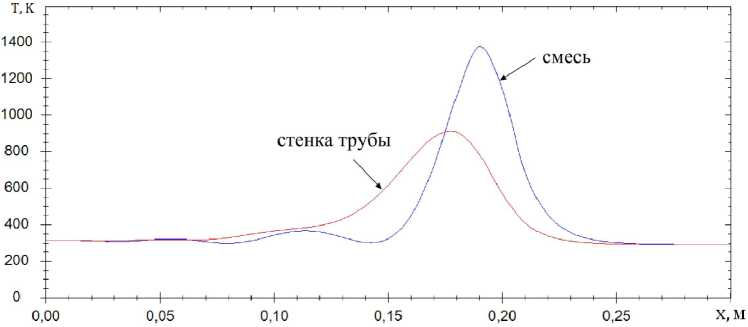
Рис. 3. Пример результатов расчета распределения температур взаимодействующих сред вдоль трубы спустя 10 с от начала процесса

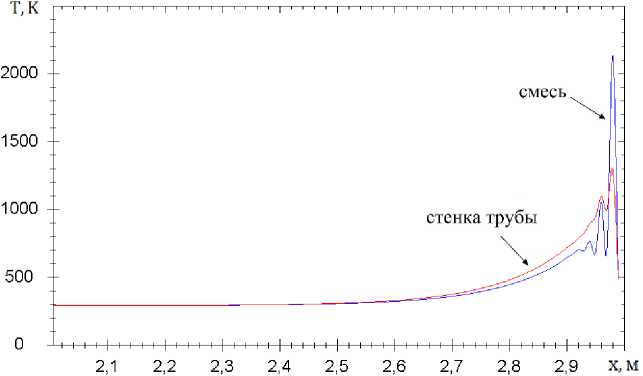
Рис. 4. Пример результатов расчета распределения температур взаимодействующих сред вдоль трубы спустя 150 с от начала процесса

Выводы

В рамках работ по построению теплофизической математической модели процесса получения слоистых металлокерамических труб с внешним металлическим и внутренним керамическим слоями с помощью СВС разработана и реализована в форме программы для ЭВМ модель теплообмена между смесью для СВС и стенкой металлической трубы.

Часть работы, связанная с термохимическими расчетами процесса СВС, выполнена при поддержке РФФИ, грант № 13-08-00545.