Теплогенератор с вихревой кавитацией рабочего тела

Введение. В настоящее время в сельском хозяйстве существует задача широкого внедрения энергосберегающих технологий, которые позволят снизить материальные средства при создании новой продукции и уменьшить энергетические затраты в данном процессе. Перспективным направлением для этого являются альтернативные источники энергии. Одним из альтернативных видов возобновляемой энергетики является вихревая энергетика [1—4], которая представляет собой технологии использования закрученных потоков сплошной среды (например, жидкости и газа) для преобразо вания их в тепловую энергию, работу, в градиент температуры и давления.

Принцип действия и конструктивные особенности ВГТ. Одним из перспективных направлений в решении этой задачи является использование вихревых гидравлических теплогенераторов (ВГТ) с использованием кавитации рабочего тела -устройств, вырабатывающих тепло посредством изменения физико-механических параметров жидкостной среды при её течении под комплексным воздействием ускоренного и заторможенного движения.

Ускорение потока достигается путем создания вихря в системах закрутки потока вихревого теплогенератора с одновременным сужением потока в конфузоре, а торможение - последующим его расширением в кавитационной трубе теплогенератора и развихрением потока на выходе из его кавитационной трубы [5]. За счет трения о поверхность корпуса скорость жидкости снижается, температура растет. Дополнительный подогрев жидкости происходит также и за счет внутреннего трения слоев жидкости, находящихся на различных радиусах от оси корпуса и имеющих разные окружные скорости.

Но основную роль в подогреве играет кавитация. За счет кавитации часть воды переходит в упорядоченное, коллоидоподобное, близкое к жидкокристаллическому состоянию, причем этот переход сопровождается интенсивным тепловыделением. Переход такого рода можно определить как фазовый переход в широком смысле и предположить, что в процессе кавитационного воздействия вода испытывает экзотермический фазовый переход с выделением избыточного тепла.

Экспериментально показано [4], что фазовый переход (гидродинамический разрыв) происходит, когда достигается величина скорости потока, при которой статическое давление в жидкости достигает величины давления её насыщенного пара. Величина этой скорости для вихревого потока вычисляется по формуле

VG = V2PG(PN - Р) / Рр, где Ро - давление насыщенного пара, Па;

Pn - исходное давление жидкости, Па;

Р - статическое давление на периферии вихря, Па;

Рр - статическое давление в жидкости.

Величина энергии, затрачиваемая на сжатие пузырька, рассчитывается из уравнения [7]:

Wc«4/37t • Р T3G, где Р - давление жидкости, при которой происходит коллапс пузырька, Па; го - радиус пузырька, м.

Сравнение величин энергий образования и сжатия пузырька водяного пара радиусом г =110"³ м и поверхностным натяжением о = 7,28 • 10"⁴ Дж/м² при 293 К показывает следующее: энергия образования пузырька Wp =9- 10"⁶ Дж при давлении разрыва (насыщенного пара) потока воды Pg= 1- 10'³ Па меньше энергии сжатия пузырька Wc =4 • 10'³ Дж жидкостью, находящейся под давлением, равным атмосферному (Р = 10"⁵ Па), в 45 раз.

Данное обстоятельство позволяет сделать вывод о том, что если гидравлическая система, в которой работает теплогенератор, открыта по давлению, то сжатие пузырька происходит под давлением окружающей среды, т.е. происходит приток энергии к жидкости из окружающей среды.

В открытой по давлению системе для получения 1 Дж энергии достаточно превратить при температуре 293 К в насыщенный пар 7,84 • 10"8 кг жидкости, а затем подвергнуть его инверсии при атмосферном давлении.

Основой вихревого гидравлического теплогенератора (ВГТ) является вихревой гидрокавитатор (рисунок 1), содержащий входное устройство, завихритель, кавитационную трубу, развихритель и выходное устройство.

Система теплоснабжения на базе вихревого теплогенератора (рисунки 2, 3) состоит из вихревой кавитационной трубы 1, теплопередающего устройства (теплообменник, батареи, калориферы и т.п.) 2, гидронасоса 3 с электродвигателем 4 и пульта управления работой вихревого теплогенератора 5.

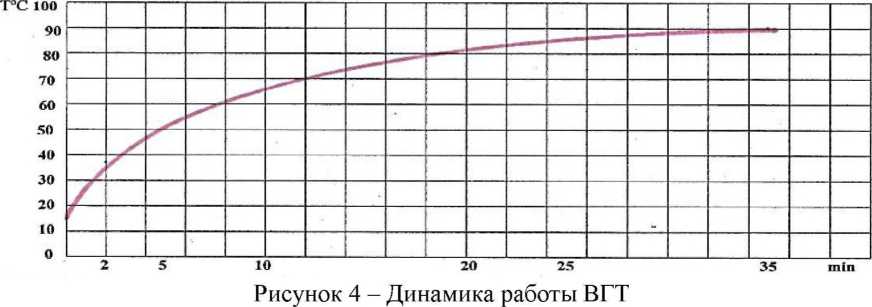
Динамика работы ВГТ представлена графиком на рисунке 4.

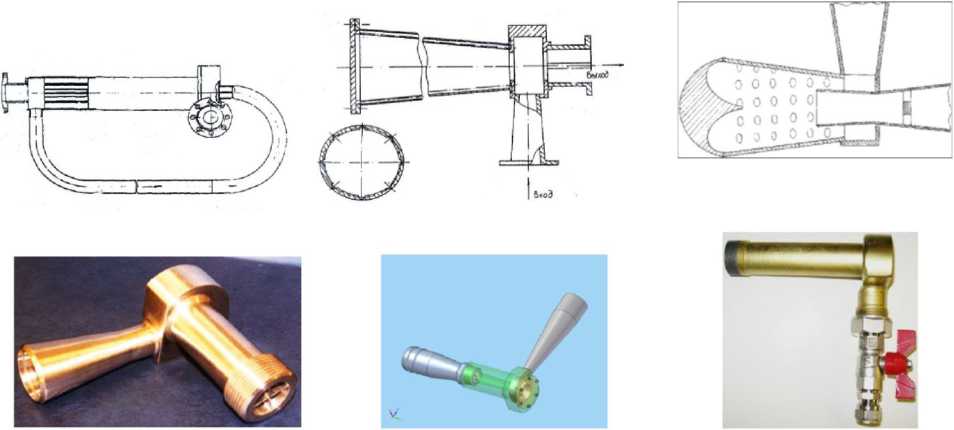
Рисунок 1 - Вихревой гидрокавитатор - варианты конструктивных схем и конструкций

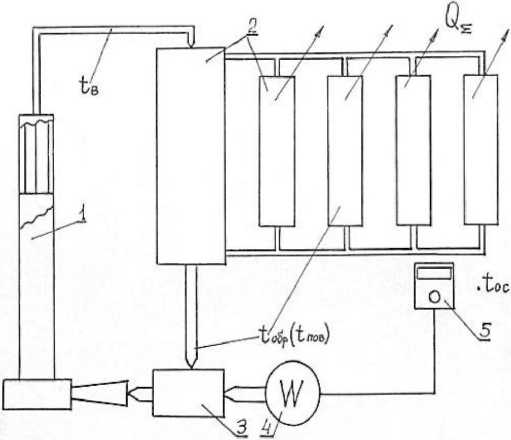
Рисунок 2 - Блок-схема системы теплоснабжения

Рисунок 3 - Варианты ВГТ

Особенности вихревых гидравлических теплогенераторов (ВГТ):

• -    устройство экологически чистое, отсутствует необходимость сжигания углеводородных топлив (уголь, нефть, газ);

• -    отсутствуют электронагревательные элементы;

• -    электроэнергия используется только для питания привода гидронасоса;

• -    отсутствует необходимость в водоподготовке;

• -    могут нагревать жидкость любого происхождения (вода, нефть, газовый конденсат ...);

• -    исключено появление отложений на внутренних поверхностях теплогенератора;

• -    могут подключаться к любой системе отопления;

• -    совмещают в одном устройстве функции нагрева и перекачивания;

• -    обеспечивают автоматическое поддержание температуры теплоносителя в заданном диапазоне температур;

• -    отсутствуют движущиеся элементы;

• -    экономичны в эксплуатации и обслуживании.

Основы теории ВГТ. Закономерности течения закрученных потоков жидкостей существенно отличаются от хорошо изученных осевых потоков [4]. Именно эти отличия обуславливают перспективы широкого применения закрученных потоков для решения инженерных задач, в частности, для систем теплоснабжения [7].

В основе предлагаемой версии расчета вихревого гидравлического теплогенератора лежит дифференциальное уравнение движения и неразрывности. Уравнение вязкой несжимаемой жидкости, в основу которого положен закон внутреннего трения Ньютона, в применении к жидкой частице имеет вид:

dC/di = F - 1/pgradP +l/pdivTn, (1) где С - скорость жидкой частицы;

• т    - текущее время;

• F    - ускорение от действия внешних массовых сил;

• р    - плотность жидкости;

Р - давление, определяющее инвариантное к ориентации в пространстве площадки, на которую оно действует, значение нормального напряжения;

Тп - тензор напряжений.

Дополняя уравнение (1) уравнением неразрывности div С= 0 и считая, что массовые силы обладают потенциалом П, т.е. F = -grad П, получим:

В тензорной форме уравнение движения турбулентного потока представляется в виде уравнений Рейнольдса с осредненны-ми компонентами скорости и их пульсаци онными составляющими С' = {С1, С'2, СЗ}.

При отсутствии внешних массовых сил эти уравнения имеют вид:

dCi/St + Cj‘5Ci/5xj = - 1/рДр/6дхі + vV2Ci + l/p’6/xj(-pOi0j),          (3)

dCi/dxj = 0, где р - осредненное во времени значение давления;

p0i0j - тензор осредненных турбулентных напряжений;

• V ² - оператор Лапласа.

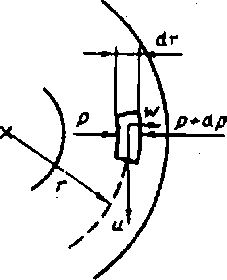
Уравнение (3) для случая движения закрученного потока в горизонтальной ци линдрической трубе удобно представить в цилиндрической системе координат Q (рисунки 5, 6) с осредненными компонентами скорости w по радиусу и по углу Ө, 0 по оси и пульсационными компонентами скорости 0', u',w'.

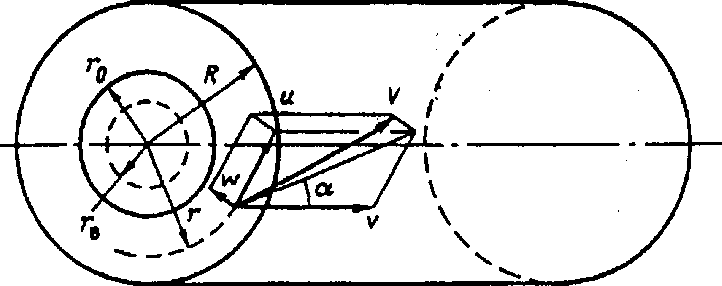
Рисунок 5 - Составляющие скорости и характерные радиусы в поперечном сечении закрученного потока в теплогенераторе

При стационарном (S/St = 0) и осе- нения Рейнольдса в цилиндрических коор-симметричном (5/5Ө = 0) течении закру- динатах могут быть представлены в виде: ченного потока дифференциальные урав- p^pV^ р^Э\\ү-ріг or         ozoz or          oz oroz p^(r^) + p^(r32) = ^(rTrz)-^(r^ or          oz or oz

• —    + — + — = 0.

. r dr dz_

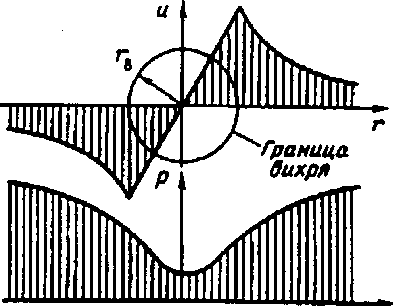
Рисунок 6 - Окружная составляющая скорости и давление в поперечном сечении закрученного потока 21

Соотношение между пульсационными компонентами скорости турбулентного закрученного потока задается в рамках одной из полуэмпирических теорий турбулентности. При ламинарном движении за крученных потоков тензор Ө'Ө' = 0 и уравнения в форме Рейнольдса переходят в уравнения Навье-Стокса. В этом случае уравнение (2) в векторной форме не изменяет вида, однако записывается в виде:

dC/dt + (C V)C = F - 1/p-gradp + vV2C.

Система совместно с уравнением неразрывности жидкости в цилиндрической систе ме координат имеет вид:

dw „dw w— + 5—		M2 _ r	1 do		^d2w Vdr2	1 + -• r	dw — + dr	d2w dz2
			p di	- + c
dr	dz
du w— dr	+ 8—-dz	wu --= и r	xd?	1 - + - r	du --+ dr	d2u dz2	\ и
dd w— dr	dz	1 dp =---- + y p dz		"d^ Vdr2	1 + -• r	d& ---4 dr	dV

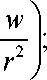
В первых трех уравнениях системы полагаем w = 0 (т.к. w « Ө и w « и), отбрасывая члены с 32/3z2, поскольку производные по z существенно меньше производных по г.

м2   1 dp г  р 6т’

Используя решение Озеена, заменим оператор Ө'5/Sz на Ө ‘S/Sz, где Ө - среднее значение осевой компоненты скорости на входе в трубу. Тогда получим систему уравнений:

_ — du    (d2u  1 55м

1)5— = ит    +у ;

dz    ^5r2  г drг,

1 др    (д^З  155)

2)5— =---- + и +;

dz    р dz 5г²    г  dr _у

3)^-(rw) + ^-(r5) = 0. dr dz

Вводя осевую компоненту вихря wzb = d/r5r(ru), получим после некоторых преобразований решение уравнения:

5 wz в/ Sz=t|t(S²wzb/ 5r²+1 /г • Swzb/ Sr), (4)

где т|т = К‘Кет-1;

R - радиус трубы.

Решением уравнения (4) является выражение:

wzb = Гн(г)/2г]тгТхр(-г²/4г]тг),   (5)

где Гн (г) - циркуляция на входе в трубу.

Соответственно, распределение окружной скорости и циркуляция определяются по формулам:

U = Гн(г)/г[1-ехр(-г2/4г|тг)];    (6)

Г = ш = Гн(г)[1-ехр(г2/4г|тг)].   (7)

Анализ (6) и (7) показывает, что при различных начальных условиях, задаваемых функций Гн(г) можно получить и различные функции изменения окружных скоростей по длине трубы. Например, при потенциальном свободном вихре на входе имеем:

Гн(г) = Const = Гн, тогда и = Гн/г[1-г2/4г|тг]. (8)

Из уравнения (8) видно, что:

• -    при г <<(4t|tz)”² в приосевой зоне жидкость вращается как твердое тело с угловой скоростью Fh/(4f|tz);

• -    при г »(4t|tz) ближе к стенкам трубы движение безвихревое, каким оно было в начальном створе.

Уравнение (8) теоретически обосновывает и составной вихрь Ранкина. Анализ решения уравнения (7) показал, что при крайних начальных условиях, задаваемых функцией Гн(г): потенциального течения -при потенциальном свободном вихре на входе и вращении потока на входе как твердого тела Гн(г) = Qhf², где Qh - начальная угловая скорость, получаются близкие результаты:

• -    при г « (Зртг)/^ жидкость вращается как твердое тело, т.е. при Vr = 0 окружная скорость U = 0;

• -    при г » (Зртг)/^ ближе к стенкам трубы наблюдается безвихревое движение.

Таким образом, при любом промежуточном состоянии жидкости на входе, какими бы законами ни задавался входящий в трубопровод закрученный поток, через определенное расстояние от начального створа вследствие вязкой диффузии и диссипации энергии сформируется течение, внутренне присущее закрученному потоку. Для окончательного определения U(R, z) примем граничные условия: U = 0 и vr = v при г = R - условие прилипания жидкости на стенках трубопровода:

u(R,r) = Fh(R)/K[ 1-ехр {- (R - f)²/4t|tz}], (9)

где т| = v/Ө = RRe"1.

В качестве граничного условия на поверхности ядра допустимо принять значения касательных напряжений равными нулю. Общее решение вида функции U(r, z) получается при применении процедуры метода скрещивания асимптотических разложений, реализуемого способом мультипликативного составления:

Так как т|т = R ReT ', окончательно имеем:

Гн(г)

г

г

1-ехр -Re,--- т 4Rr

• 1-ехр -Re

'т 4Rr

(И)

В принятой модели определенную сложность при инженерных расчетах вызывает назначение турбулентного числа ReT = 6R/vt, где vt - определяется из экс перимента. Часто принимают vt = vaRe. где а = 2,46" 10”3. Тогда получим распределение в сечении потока:

где Ря - давление в полом вихревом жгуте закрученного потока;

го - радиус цилиндрического разрыва сплошности вблизи оси вращения, при г < го давление Р(г) = Ри = const.

По известным значениям p(r, z) и w(z), а также из начального условия, задаваемого функцией распределения по радиусу удельной энергии частиц жидкости во входном сечении трубопровода Нн(г), определяется по (И) функция распределения осевой компоненты скорости потока по длине и текущему радиусу трубопровода v(r, z). Из уравнения (10) по известным v определяется распределение радиальной скорости W(r, z).

Таким образом, для кольцевого вязкого турбулентного закрученного потока несжимаемой жидкости в горизонтальном цилиндрическом трубопроводе при заданных граничных (условие прилипания жидкости на стенке) и начальных условиях на входе при z = 0, задаваемых функциями Гн(г) b Нн(г), в каждом конкретном случае могут быть получены распределения всех компонент скорости, давления и радиуса вихревого жгута в функции расстояния от начального створа и текущего радиуса: v(r, z), u(r, z), w(r, z), p(r, z), ro(z). Интенсивность закручивания потока в точке определяется углом скоса L между направлениями осевой и полной скорости:

А = arcos(0/v) = arctg(u/0). (13)

По оси потока формируется вихрь, который наблюдается по всей длине водовода в виде вихревого шнура радиусом гв. Вихрь может быть полым или полностью заполненным жидкостью. Исходя из математического описания жидкости в сечении, проведенном нормально оси потока, выделяют область вихревого движения г < ш, и вне вихревого шнура область невихревого кругового движения г > ш.

Особенностью вихревого движения является вращение элементарных частиц жидкости вокруг своих мгновенных осей. При круговом движении такое вращение отсутствует, и, следовательно, оно является потенциальным. В действительности поток реальной жидкости всюду вихревой.

В пределах вихревого шнура все частицы жидкости вращаются вокруг собственных осей с угловой скоростью Q. Закон распределения окружных скоростей выражается законом вращения твердого тела:

U = Qr.            (14)

Для определения давления р в закрученном потоке используется уравнение Эйлера:

u2/r = 1/pSp/Sr, (15) интегрируя его по г, получим давление внутри вихревого шнура:

Р = р‘(н2-ив2)/2 + рв. (16)

Для большинства жидкостей зависимость плотности от температуры можно представить в виде:

р = рш - ог(Т - Тш), (17) где индекс т - средняя величина плотности, величина а - очень мала.

Для воды изменение плотности составляет около 1% при t от 0 °C до 50 °C и 3% при t от 50 °C до 100 °C [И].

Оценка эффективности работы ВГТ. Основой инженерной методики определения эффективности ВГТ является «эк-сергетический метод термодинамического анализа технических систем преобразования энергии и вещества» [4], в соответствии с которым эффективность системы теплопреобразования в ВГТ оценивается:

• а)    коэффициентом преобразования энергии (КПЭ):

ц= Q27W, где QZ - полная теплопроизводительность системы;

W - затраченная электроэнергия;

• б)    коэффициентом полезного действия:

КПД = QZ Kp/W = ц-Кр, где Кр = 1 - Тос/Тв - коэффициент работоспособности тепла.

Полная теплопроизводительность системы оценивается как

QZ = Q1+Q2, Дж, где Q1 - количество тепла, отведенное в период работы гидронасоса;

Q2 - количество тепла, отведенное в период, когда гидронасос не работает (пауза).

Количество тепла, отведенное из системы в период работы гидронасоса:

Q1 = Gp-Cp-Atl-тр, Дж, где Gp - расход воды в период работы гидронасоса, кг/с;

Ср - теплоёмкость воды, ккал/кг-град, Atl = tB - to6p - разность температуры воды в прямой и обратной магистралях, °C;

тр - время работы гидронасоса в каждом цикле, с.

Количество тепла, отведенное из системы в период, когда гидронасос не работает:

Q2 = Ғ-ос-Аі2-тп- -10"3, Дж, 4,19

где F - теплопередающая поверхность установки, м2,

At2 = tnoB - toe - разность температур поверхности установки и окружающей среды, °C;

тп - время, когда насос не работает (пауза), с;

ос - коэффициент теплопередачи, Вт/м2К.

Для определения ос необходимо вычислить значение критерия Нуссельта (Nu) по формуле [8]:

Nu = c(Gr-Pr)n, где с, п — постоянные числовые коэффициенты;

Кр

Работа: L = ҺЗ - Һ4 (площадь F1234).

Тепло: Q = ҺЗ - Һ2 (площадь Ға23б).

Gr - число Грасгофа;

Рг - число Прандля.

Для этого, с учетом At2 = Іпов - toe, по [9] определяем X, v и Рг, где А - коэффициент теплопроводности, вт/м-К;

v - коэффициент кинематической вязкости, м2/с.

Далее по формуле

Gr = 0- d3 • g-A t2 / v2 вычисляем число Грасгофа, где 0 - температурный коффициент объемного расширения, 1/К (определяется по таблице [10]), где d - диаметр корпуса ВГТ, м; g - ускорение свободного падения, м/с2.

Определив величину произведения (Gr-Pr), по [И] находим значения коэффициентов с, п и по формуле Nu = c (Gr Pr)n определяем значение критерия Нуссельта.

Значение коэффициента теплопередачи ос находится по формуле oc = Nu -X/ d.

Под работоспособностью, или эксергией тепла, понимают то возможное количество технической работы, которое в состоянии совершать данная термодинамическая система, находящаяся в заданном начальном состоянии, при условии, что все совершаемые системой процессы изменения состояния обратимы и осуществляются до конечного термодинамического состояния, равновесного с окружающей средой, т.е. - какое количество работы L может быть получено в идеальном (обратимом) процессе от любого количества тепла Q.

Отсюда

L/Q .

Следовательно: Кр = Ғ1234/ Ға23б = (Т - Тос)-AS/ T AS =(Т - Тос)/ Т = 1 - Тос/ Т.

Для децентрализованных систем теплоснабжения, производящих тепло Q на температурном уровне Тв, коэффициент работоспособности тепла определяется как

Кр = (Тв - Тос)/ Тв = 1 - Тос/ Тв, где Тв - температура нагретой воды, К;

Тос - температура окружающей среды, К.

Таким образом, если коэффициент преобразования энергии ц = QZ/W оценивает только количество полученного тепла на единицу затраченной энергии, то КПД, учитывающий работоспособность этого тепла, оценивает его качество, т.е. температурный уровень Т, при котором производится тепло Q.

Параметры децентрализованных систем теплоснабжения на базе ВГТ

	и	и	и	І б Й н У s о 9 сз о. о о < 1 о	и Н о 1s О Он Ое И Н 5 <] 03 К	d Он ^ К S & и Ң Он сЗ У к Н 5 91 1	S К сЗ а и X	о о сЗ о	5 1 а	m 8	5 1 су	І СУ	О.	ь" и і и	ё
55	18	51,62	45,5	60	50	41,5	1,47	152,4	544,2	10,8	539,1	1083	1,8	0,1	19
7,5	12	65	50	495	2163	0,975	0,055	4,5	480,4	8,2	1010,5	1490	1,77	0,157	28
37	18	53,3	48,3	240	708	13,0	0,1625	4,8	178,75	8,4	240,5	419	2,3	0,108	24,3
37	18	50,5	45,5	190	732	10,6	0,1625	4,8	154,4	7,8	212,5	367	2,4	0,89	21,4
22	16	45	41	15,5	66	3,5	1,И	4,0	68,8	14,	26,0	94,8	1,9	0,09	17,2

Для примера, по параметрам таблицы, снятым при испытании некоторых децентрализованных систем на базе ВГТ, рассчитаны коэффициенты преобразования тепла (ц) и КПД.

При различных режимах работы системы, коэффициент преобразования тепла ц менялся в пределах 1,77-2,41, при этом КПД составлял 17,2-28%. Энергетический баланс децентрализированной системы определяется как

Q = W + Qq, где W - электроэнергия, затраченная на привод гидронасоса, кВт-ч;

Qq - дополнительное тепло, подведенное к системе, (Дж).

Одним из примеров подвода дополнительного тепла в систему является работа теплового насоса (TH).

В данном случае дополнительное тепло Q отводится из испарителя, т.е. Qq = Qo. Если в систему дополнительное тепло Q не подводится, то Qq = 0, т.е. полученное количество тепла Q равно количеству подведенной энергии: Q = W. Этот вариант наблюдается во всех электронагревательных приборах (ТЭНах, эл. котлах, эл. печах и т.д.). В этом случае, коэффициент преобразования тепла ц = 1, а КПД = ц- Кр = Кр. Так, если при температуре окружающей среды toe = 18^-20 °C, температура горячей воды в системе отопления tB = 55-60 °C, то Кр = 0,113-0,127.

Таким образом, всё электронагревательное оборудование, используемое для нагрева воды, при указанных температурах имеет КПД= 11,3-12,7%.

Выводы. В России в настоящее время активно расширяется производство и эксплуатация вихревых теплогенераторов, причем наиболее активно в местах, где отсутствует централизованная система теплоснабжения. По себестоимости тепловой энергии лучшие модификации ВГТ приближаются к газовым котельным, которые сейчас являются самыми дешевыми производителями горячей воды. Эти и другие преимущества ВГТ (по сравнению с традиционными) вызывают большой интерес у потребителей, т.к. у них появляется возможность существенно улучшить экологические и экономические показатели как промышленных предприятий, так и коммунального сектора.

Предложенный вариант теоретических основ работы ВГТ и способ оценки эффективности работы ВГТ, основанный на использовании эксергетического метода термодинамического анализа тепловых систем, лежит в основе создания конструктивного ряда ВГТ.

Вихревой гидравлический теплогенератор перспективно использовать в качестве автономной системы отопления и теплоснабжения в различных областях жизнедеятельности:

• -    объекты сельского хозяйства;

• -    коттеджные массивы;

• -    складские помещения и т.д.

ВГТ обеспечивает экологическую чистоту процесса выработки тепла, минимальные потери тепла при передаче его потребителю и высокую экономическую эффективность.