Тепломассообмен и гидродинамика при лазерном оплавлении металлов
Автор: Вотинов Г.Н., Цаплин А.И.
Статья в выпуске: 5, 1997 года.
Бесплатный доступ
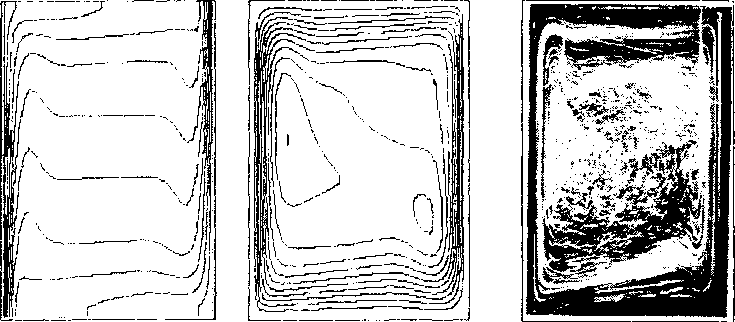
На основе сопряженных уравнений тепломассопереноса сформулирована математическая модель процесса плавления металла концентрированной лазерной энергией. Принять во внимание влияние конвекции Марангом на расплавленное смешение металла. / показана адекватность математической модели данным физического эксперимента. Приводятся результаты расчета эксперимента - изолинии функции потока и изотермы.
Короткий адрес: https://sciup.org/146211768
IDR: 146211768 | УДК: 536
Текст научной статьи Тепломассообмен и гидродинамика при лазерном оплавлении металлов
аюат
---+ V ■ Vro - А ю + Gr---, (2) atax co = - A\|/,(3)
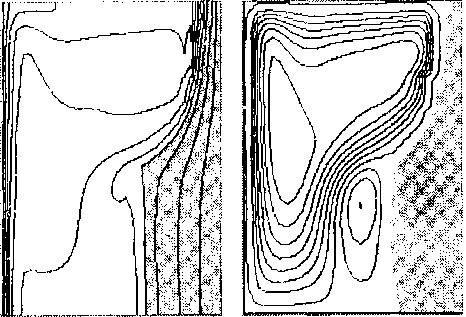
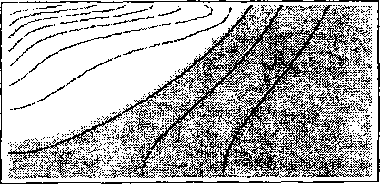
где T - температура, m - завихренность, су - функция тока, V - скорость, Pr = v0/%3 , Gr = g pATL3/v02 - критериальные комплексы Прандтля и Грасгофа, v0 - кинематическая вязкость, Хэ=^о/(рсэ) ' эффективная температуропроводность, g - ускорение свободного падения, р - коэффициент объемного расширения, ДТ - характерная разность температур, L - характерный линейный размер, X - коэффициент теплопроводности, р - плотность, сэ - эффективная теплоемкость.
Плотность принята линейно зависящей от температуры:
Р=Ро[1-Р (Т-Тф)], где ТФ = (Tl+Ts)/2 - температура фазового перехода, Tj„ Ts - температуры ликвидуса и солидуса соответственно.
Эффективная теплоемкость в соответствии с квазиравновесной теорией двухфазной зоны с учетом удельной теплоты фазового перехода Q может быть определена по формуле
[с, T
3 с + -^~ TS Функция тока связана с компонентами скорости соотношениями: 5 о iy , v = -—. О у О X Краевые условия включают в себя начальные Т (t—0) = То, (о (t=0) = vy (t=0) = 0 (4) и граничные условия: аТ ат ау г ат Эх _ ат г Эх 1 з = 0; Г ат - q - « (тп - тс), Г1 где Тп, Тс температуры поверхности и окружающей а = Ео(тй+Т^)(тп+Тс) - коэффициент теплоотдачи излучением, е - среды, степень черноты, су - коэффициент излучения абсолютно черного тела, q = f (X) - плотность потока энергии лазерного излучения. На свободной поверхности граничное условие для завихренности имеет вид [5] ®lr,=Mnj|, (6) СУдр^тТАТ где Мп = —---- число Марангони, определяющее интенсивность термо- PVX капиллярной конвекции, оу - коэффициент поверхностного натяжения, рпт -температурный коэффициент поверхностного натяжения. На оси симметрии ™1г5 = 0,(7) на твердой границе завихренность вычисляется из уравнения Пуассона для функции тока ®|р6 =-А^-(8) Из условия непроницаемости функция тока на границе жидкой фазы должна быть постоянной, в частности нулевой, 'Р'|г = 0.(9) Нелинейность дифференциальных уравнений обусловлена не только наличием конвективных членов, но и неоднородностью теплофизических свойств стали в широком интервале температур. Другой особенностью является сопряжённость, предполагающая совместное решение системы уравнений (1-3). Сопряженность и нелинейность системы уравнений (1-3) с краевыми условиями (4-9) существенно затрудняют решение краевой задачи и предполагают использование численных методов с дальнейшим вычислительным экспериментом на ПЭВМ Особенности численной реализации Поставленная задача реализована методом сеток Применена неявная однородная конечно-разностная схема с расщеплением двумерной задачи на последовательность одномерных, которые затем решались продольно-поперечной прогонкой по схеме сквозного счета без явного выделения границы раздела фаз. Подвижная граница раздела фаз определялась по положению изотермы Т = Тф. При несовпадении криволинейной границы раздела фаз с узлами сетки применялись разности с переменными шагами по координатам для функции тока и завихренности [4]. Завихренность жидкой фазы на твердых границах вычислялась с помощью двухконтурной методики В Л. Грязнова и В И. Полежаева [6], при которой обеспечивается выполнение условия “прилипания”. Конвективные члены в уравнениях переноса (1-2) аппроксимировались с помощью консервативной схемы с донорными ячейками. Эта схема дискретизации конвективных членов позволяет по сравнению с другими достигать установления с наименьшими затратами машинного времени [4]. Для решения разностного аналога уравнения Пуассона (3) применялся метод последовательной линейной верхней релаксации с оптимизацией параметра релаксации [7]. Тестирование модели Проверка математической модели проводилась сравнением с экспериментами по намораживанию воды в прямоугольной области с двумя изотермическими и двумя адиабатными границами в соответствии с работой [4] На рис.2,в представлены результаты изучения тепловой конвекции воды в прямоугольной области без изменения ее агрегатного состояния в интервале температур 14/1-16,2 °C; вода, нагреваясь у левой границы, движется вверх и. охлаждаясь, опускается вниз вдоль правой границы, образуя замкнутый контур циркуляции. Па рис 3,в показаны результаты эксперимента по намораживанию воды в условиях конвекции жидкой фазы в прямоугольной области с непроницаемыми границами. Вертикальные границы - изотермические с температурами Ть Г., а горизонтальные - адиабатные При температуре Т2, меньшей температуры фазового перехода Тф, на правой вертикальной поверхности образуется корка льда, толщина которой 5 в бесконвективном приближении постоянна, а граница затвердевания -вертикальная линия Свободная конвекция жидкой фазы приводи! к перераспределению энергии и отклонению границы затвердевания о г вертикали Толщина твердой фазы становится переменной. Влияние конвекции сказывается в неравномерном нарастании корки по высоте области. а б в Рис. 2. Свободная конвекция воды в прямоугольной области: Ti = 16,2°C, Т2М4,1 °C; а, б - расчетные изотермы и линии тока. Сетка 40x40, в - физический эксперимент Жидкая фаза циркулирует с образованием двух устойчивых вихрей, причём в верхней части области у границы затвердевания отмечается движение воды вниз, а в нижней части - вверх. На стыке двух вихрей толщина твёрдой фазы максимальна. Расчел проводился для дистиллированной воды со следующими тенлофизическими характеристиками: коэффициент теплопроводности и теплоёмкость зависят от температуры (по шкале Цельсия) и изменяются скачкообразно при переходе через границу затвердевания | 2,21 -0,0115 • Т, Т<.ТФ, [2090 + 5,2Т, Т<ТФ, ~ ] 0,569+ 0,0016-1, Т + Тф, С [4212-1,1 Т. Т > Тф Плотность аппроксимируется параболической зависимостью, отражающей ее инверсию в рассматриваемом интервале температур: р=ро( 1 +6,3 • 10"5Т-7,4991 • 10"6?2), где р0=999,841 кг/м3- плотность воды при 0°С. Плотность льда 917,345 кг/м'. Коэффициент объёмного расширения 0 = (0,15 Т-0,63)-10"4, 1/°С Кинематическая вязкость воды v=l,429 10"6 м2/с. Рис.З. Намораживание льда на правой стенке канала при Ti=14,5°C, Т2=-6,7°С: а, б - расчетные изотермы и изолинии тока Сетка 40x40; в - физический эксперимент. При обезразмеривании в качестве характерного линейного размера используется высота области L=b, в качестве характерной разности температур в случае свободной конвекции: AT=Ti-T2, при затвердевании: АТ=Т1-ТФ. Система уравнений (1-3) замыкается граничными условиями: б? Т 5 т Т (0,у) = Ть Т (а, у) = Т2, L— (х,0) = ^(х,Ь) = 0, V (0,у) = V (а-5, у) = у (х, 0) = у/ (х, Ь) = 0. Граничные условия для завихренности на твердых поверхностях, ограничивающих жидкую фазу, определяются из уравнения Пуассона (3). На рис.2,а,б представлены результаты численного исследования свободной конвекции, а на рис.3,а,б — процесса затвердевания. Максимальное отличие толщины корки льда, полученной расчетным путем, от наблюдаемой в эксперименте не превышает 12%. Погрешность в расчете границы затвердевания непосредственно связана с ошибками в определении скоростей: максимальная расчетная скорость составляет 1,9 КУ3 м/с и отличается от фактической почти на 15%. Сравнение результатов расчета с экспериментальными данными подтверждает адекватность математической модели и возможность ее применения для расчетов тепломассообмена в задачах с фазовым переходом. Некоторые результаты вычислительного эксперимента Вычислительный эксперимент проводился для среднеуглеродистой стали (сталь 45) при следующих исходных данных: Хж~28,8 Вт/(м-К); ^=30 Вт/(м-К); сж=630 Дж/(кг-К); ст=680 Дж/(кг-К); рж=6900 кг/м3; рт=7200 кг/м3; v0=l,429-10^ м2/с; 3=6-10 5 К'1’ Q=2,7-105 Дж/кг; Т,=1496,5 °C, TS=1442,6 °C; Тф«1470 °C; Тс=20 °C, а= 1,2-Ю"3 м; Ь = 0,5-10"3 м; ст0=5,67-10 Вт/(м К ); Е=0,8; Мп=100, q| г(=6-108-ехр(-х2/2) Вт/м2 при хе(0,З а/4]. В качестве характерных масштабов были выбраны следующие параметры: линейный размер - высота области L=b, кинематическая вязкость V характерная разность температур АТ=ТтТф, где Тт=2500 °C. При воздействии на металл потоком энергии лазерного излучения происходит интенсивное проплавление его поверхности При этом тепло распространяется вглубь металла и излучается с его поверхности. Конвекция приводит к искривлению изотерм (рис.4). Расчетная максимальная скорость конвективного перемешивания жидкой фазы при указанных исходных данных и импульсе длительностью 2,5 мс достигает 0,95 м/с. Рис. 4. Результаты вьиислительного эксперимента на сетке 80x70 через 2,5 мс после включения лазера, а - изотермы: Ттах=2450°С> ТПЦП=97°С; б - изолинии тока vymm=-9,5; ^^х^О. Изолинии построены через равные интервалы Разработанная математическая модель позволяет детально описывать теплофизику оплавления металла и может быть использована для прогнозирования лазерного воздействия в конкретных технологических условиях.