Тепломассообмен и сопротивление при внутренних течениях многокомпонентных химически реагирующих газовых смесей

Исследование тепломассопереноса при течении в каналах и трубах многокомпонентных химически реагирующих газовых смесей является одной из важных проблем конвективного тепломассообмена, получившей развитие в связи с потребностями современной науки и техники: энергомашиностроения, ядерной энергетики, ракетных и космических исследований, химической промышленности, экологии.

Изучение происходящих при движении многокомпонентных газовых сред в трубах, реакторах и резонаторах газодинамических и химических лазеров химических реакций, турбулентности и процессов обмена энергией между различными степенями свободы молекул является составной частью оптимизации технологического процесса, определяющей его эффективность и работоспособность. Указанные обстоятельства многократно повышают требования к детализации описания газодинамических и физико-химических процессов в таких устройствах. При анализе течений в реакторах необходима достоверная информация не только о полях скоростей, давлений, температур, но и о концентрациях компонент смеси.

В свете достигнутых результатов в отечественном и зарубежном реакторостроении в последнее время особенный интерес приобретает изучение явлений тепломассопереноса в химически реагирующих газовых системах. Многочисленные теоретические и экспериментальные исследования показали большую перспективность применения химически реагирующих (диссоциирующих) газовых систем в качестве рабочих тел энергетических установок и теплоносителей ядерных реакторов атомных электростанций ( Красин , 1970; Петухов и др. , 1974; Колыхан, Нестеренко , 1977; Петухов , 1987). В настоящее время известны и изучаются свыше пятидесяти перспективных химически реагирующих газовых систем, обладающих высокими теплофизическими свойствами, а также значительными изменениями молекулярной массы и газовой постоянной в процессе прохождения газом общего цикла газотурбинной установки. Высокие теплофизические свойства многокомпонентных химически реагирующих газовых смесей обусловлены тем, что в диссоциирующем газе перенос тепла осуществляется не только за счет обычных механизмов (теплопроводность, конвекция), но также и за счет химической энергии (энтальпии), переносимой при диффузии отдельных компонент реагирующей смеси.

Изучение конвективного тепломассообмена в многокомпонентном химически реагирующем газе представляет и большой научный интерес. Принципиальное значение, прежде всего, имеет изучение взаимосвязанных явлений химических превращений и переноса тепла и массы. Это относится, в первую очередь, к турбулентным течениям, в которых взаимное влияние неравновесных химических превращений и турбулентности может привести к существенным воздействиям на характеристики и интенсивность теплообмена. Изучение течений многокомпонентных химически реагирующих газов позволяет также выяснить характер влияния химических реакций на теплоотдачу, что особенно важно в случае неравновесных течений ( Петухов , 1987; Лапин, Стрелец , 1989).

Проблема адекватного описания турбулентных течений многокомпонентных химически реагирующих газовых смесей до настоящего времени остается одной из самых сложных проблем в прикладной физике. Многие стороны этой проблемы не только не исследованы теоретически и экспериментально, но даже не достигли того уровня конкретизации, который позволил бы говорить о завершении этапа постановки задачи. Сложность рассматриваемой проблемы связана как с незавершенностью теории турбулентности, так и со специфическими особенностями турбулентных течений с химическими реакциями, заключающимися в чрезвычайно сложном характере взаимного влияния процессов турбулентного переноса и многокомпонентного химического реагирования (Петухов, 1987; Лапин, Стрелец, 1989).

Основные проблемы, возникающие в задачах о течениях многокомпонентных химически реагирующих газовых смесей, состоят в следующем. Прежде всего, отметим существенные нелинейности, связанные с зависимостью источниковых химических членов от температуры. Значительной математической сложностью отличается описание диффузионного массопереноса в многокомпонентных газовых смесях. Термодинамические и переносные свойства многокомпонентной реагирующей смеси определяются не только локальными значениями температуры и давления, но и ее составом, рассчитываемым в процессе решения всей задачи. Это обстоятельство относится не только к химически неравновесным течениям, но и к равновесным потокам многокомпонентных газовых смесей, так как различие в диффузионных свойствах отдельных компонент приводит к нарушению условия постоянства состава смеси из химических элементов (элементарного химического состава). Этот эффект называется эффектом диффузионного разделения отдельных химических элементов в многокомпонентной газовой смеси с различными диффузионными способностями компонент. Поэтому химический состав многокомпонентной газовой смеси будет зависеть не только от локальных значений температуры и давления, но и от концентраций отдельных химических элементов, из которых состоят компоненты данной смеси.

Следует отметить, что для проведения расчетов коэффициентов динамической вязкости, теплопроводности и диффузии многокомпонентных газовых смесей необходимо знать потенциалы межмолекулярного взаимодействия. Однако, во многих случаях эти потенциалы известны еще недостаточно, что приводит к нестрогости при выборе потенциальной функции межмолекулярных взаимодействий и неточности вычисления интегралов столкновений при расчете переносных свойств ( Curtiss, Hirschfelder , 1949; Curtiss , 1968).

Описание турбулентных течений в настоящее время почти полностью опирается на те или иные полуэмпирические теории, позволяющие рассчитывать коэффициенты турбулентного переноса ( Петухов , 1987; Лапин, Стрелец , 1989; Лапин и др. , 1995). Хотя для ряда практически важных случаев течений разработаны эффективные полуэмпирические методы расчета, возможность их использования для турбулентных реагирующих потоков не очевидна, так как химическая неравновесность может оказать влияние на турбулентный перенос. В этих условиях для определения характеристик турбулентности целесообразно привлекать балансные уравнения для вторых моментов, содержащие члены, связанные с пульсациями химических источников ( Лапин, Стрелец , 1989). Другая важная сторона взаимодействия турбулентности и химических реакций состоит в том, что пульсации температуры и состава смеси влияют на интенсивность химических превращений. Указанные явления могут оказать воздействие на интенсивность процессов тепломассопереноса в турбулентных реагирующих потоках. Таким образом, при описании турбулентных течений многокомпонентных химически реагирующих газовых смесей требуется учет ряда специфических эффектов, а для решения таких задач необходимо использовать специальные эффективные методы преодоления существенной нелинейности исходной системы дифференциальных уравнений. Поэтому ограничимся сначала рассмотрением вязких течений многокомпонентного химически реагирующего газа, когда может иметь место диффузионное разделение химических элементов.

• 2.    Математическое описание течения и тепломассопереноса при химических превращениях

  Рассмотрим уравнения сохранения, описывающие течение вязких многокомпонентных химически реагирующих газовых смесей, воспользовавшись при этом некоторыми результатами работ ( Суслов и др. , 1971; Лапин, Стрелец , 1989), где уравнения динамики вязкого многокомпонентного газа представлены в наиболее полном виде. В ряде случаев наиболее удобной оказывается тензорная форма уравнений переноса, использующая индексы для обозначения проекций величин на оси координат s j . Дважды повторяющиеся индексы будут означать суммирование по значениям 1, 2, 3 компонент векторов и тензоров, соответственно, по осям x , y , z . Однако на индекс i , используемый для обозначения номера компоненты смеси, это правило не распространяется.

Уравнение неразрывности для смеси газов в случае стационарного установившегося течения при отсутствии массовых сил в этих обозначениях будет иметь вид

a

— (pv j ) = 0. ^d s j

Уравнение переноса количества движения можно представить в форме ( Лапин, Стрелец , 1989)

a <     .

— (PVVk) = -aSj

dp   St jk dSk    dSj  ’

где T jk - тензор вязких напряжений, определяемый выражением

2       j

^T jk = ^{- 5}jk" ^^ + ^Ц

^j ₊5V k а $_k   a s j

в котором 8 j _k - символ Кронекера ( ^ _k = 1 при j = k , 8 j _k = 0 при j * k ).

Уравнение неразрывности для i -й компоненты смеси в дивергентной форме примет вид

a

— ( P VC) = w i ^d s j

Уравнения переноса энергии можно записать в виде

8 z M     dp

— ( p v j h) = V k — + d Sj             d S k

-

J ij .

5 s j

Tk  ъ dsj

-

d q

⁸ s j

.

В уравнениях (1) - (5) введены обозначения: v - среднемассовая (гидродинамическая) скорость; р - плотность смеси; р - давление смеси; ц - коэффициент динамической вязкости смеси; c i - массовая концентрация i -й компоненты; w i - массовая скорость изменения концентрации i -й компоненты в химических реакциях; J i - плотность потока массы i -й компоненты (диффузионный поток i -й компоненты); h - удельная энтальпия смеси; q - плотность потока тепла.

К системе уравнений (1) - (5) необходимо добавить уравнение состояния для смеси

Nк с р = pRT 2 —.                             (6)

• i = 1 mi

Здесь Т - температура; R - универсальная газовая постоянная; m i - молекулярная масса i -й компоненты; N_K - число компонент смеси.

Отметим, что из N_K уравнений неразрывности для компонент смеси (4) только N_K - 1 являются независимыми, так как концентрации компонент с_i связаны дополнительным условием

N к

2 с , = 1,                                                   (7)

i = 1

вытекающим из определения массовой концентрации i -й компоненты

Ci = Pi / P, где pi - парциальная плотность i-й компоненты смеси.

Рассмотрим уравнение диффузии для i -й компоненты смеси (4). Для описания состава N к -компонентной химически реагирующей газовой смеси необходимо использовать N_K - 1 уравнений диффузии (4) и условие (7). Если рассматриваемая N_к -компонентная смесь состоит из N _э химических элементов, то число уравнений диффузии для компонент (4) можно без ущерба для строгости постановки задачи уменьшить на N э - 1 уравнений, заменив недостающие N э - 1 уравнений уравнениями диффузии для N э - 1 химических элементов.

Введем в рассмотрение концентрацию k -го элемента в i -й компоненте смеси

C ki = m k N ki / m i .                                                      (9)

Здесь m_k - атомная масса k -го химического элемента, N_ki - число атомов k -го элемента в i -й компоненте, m i - молекулярная масса i -й компоненты.

Умножая уравнение диффузии для i -й компоненты смеси (4) на с ki и производя суммирование по всем N к компонентам смеси, получим N э уравнений диффузии для N э химических элементов

( p v j c k* ) = - A ^J *kj .                                   ⁽¹⁰⁾

• a s j              a s j

Здесь                                            C k = X c ki ^C i                                            (11)

i = 1

• -    концентрация k -го химического элемента;

N к

J kj = X C ki J ij                                            (12)

i = 1

• -    диффузионный поток k -го химического элемента в проекции на ось j , а c ki w, = m ki - массовая скорость перехода элемента k в состав i -й компоненты.

Так как в процессе химической реакции масса любого k -го элемента сохраняется, то N к

X c ki w i = w k   0.                                       (13)

i = 1

Одно из уравнений (10) может быть заменено на очевидное условие

N э

• х c k = 1.

k = 1

В рамках строгой постановки задача определения состава движущейся многокомпонентной смеси сводится к необходимости интегрирования N_K - N _э уравнений диффузии для компонент (4), N э - 1 уравнений диффузии химических элементов (10) и использования одного из условий (7) или (14).

Для расчета процессов многокомпонентной диффузии удобно использовать так называемые эффективные коэффициенты диффузии D i , впервые введенные в работах ( Тирский , 1963, 1964) в практику расчетов ламинарного пограничного слоя с химическими реакциями. В соответствии с принятым в работе ( Тирский , 1964) рассмотрением, выражение для эффективного коэффициента диффузии i -й компоненты может быть получено из N_K - 1 независимых соотношений Стефана - Максвелла ( Тирский , 1964; Лапин, Стрелец , 1989) и формальной записи диффузионного потока в многокомпонентной смеси в виде закона Фика

Jij = - p ciVij = - p Di     , d sj

где Jij - диффузионный поток i-й компоненты в проекции на ось j; Vj - проекция вектора скорости диффузии i-й компоненты на ось j.

Эффективный коэффициент диффузии i -й компоненты в многокомпонентной смеси может быть определен по одному из следующих равенств

^Nк m с       V     ^Nк ^Nк m с

D i ^- 1 = X       1 1 - т т 1+ X C k X        V i^ T k- =

• j=1 mjDij V   ViJ k=1 j=1 mjDkj

Nк m с,  । cJ)    Nк    Nк  m Cj | cJ,)

= X —-11--i-j l+X Ck X ——I ^j - ciJk I.(16)

• j =1 m j D ij V    - j - i J    k T1   F=1 m j D kj V c- i   C k - i J

Из определения эффективных коэффициентов молекулярной диффузии (16) следует, что в общем случае эти коэффициенты, выражающиеся через бинарные коэффициенты диффузии D_i j , зависят от состава смеси и отношения диффузионных потоков компонент, т.е. от определяющих параметров конкретной задачи. Это обстоятельство не является существенным и фактически не усложняет проведение конкретных расчетов в рамках численных итерационных методов.

Если ввести эффективные числа Шмидта

X ^-i = ⁰

i = 1

то из равенств (12), (15) и (17) будем иметь

Sc , = ц / p D i ,                                        (17) N K c ki  d Ci - kj = - ц X^- iF - .                              (18) i = 1 Sc i  d s j

В любой точке многокомпонентного химически реагирующего потока должны выполняться условия N к

Nэ

и

У Jу = 0.

kj k=1

Из последнего выражения с учетом равенства (18) получаем

1 NN^ c   ас_ = 0.

1 1 Sci dsj

Если эффективные числа Шмидта всех компонент одинаковы

Sci = const = Sc, то из равенства (21) с учетом (22) следует, что

Nэ gc* 1^ = 0, k =1 dsj т.е. концентрации всех химических элементов в многокомпонентной смеси должны оставаться постоянными

*

c_k = const.

В случае, если эффективные числа Шмидта компонент смеси различны, то из равенства (21) после его интегрирования должно следовать, что ck = Ф (Sj, c.),                                                   (25)

т.е. концентрации отдельных химических элементов в потоке будут переменными, зависящими не только от координат s j , но и от состава смеси. Таким образом, состав многокомпонентной реагирующей смеси в общем случае течения определяется функцией

• c . = f ( S j , c k , p , T) ,                                                (26)

• 3.    Анализ кинетического эффекта диффузионного разделения отдельных химических элементов в многокомпонентных газовых смесях

т.е. распределение концентраций компонент в пространстве sj будет зависеть не только от локальных значений давления и температуры, но и от новых определяющих аргументов - концентраций отдельных химических элементов.

При расчете течений многокомпонентных реагирующих газовых смесей в большинстве проведенных в этой области исследований было принято приближение, согласно которому частицы объема газа рассматривались как термодинамически закрытые системы, т.е. системы, состав которых из химических элементов (элементарный химический состав) остается неизменным. В этом случае концентрации отдельных химических элементов в потоке полагались постоянными, а при определении состава газа в каждой точке потока использовались либо таблицы термодинамических функций, составленные для определенного элементарного состава газа, либо выражения для констант равновесия независимых химических реакций, в которых концентрации химических элементов предполагались заранее определенными.

Присутствие в многокомпонентном химически реагирующем газе компонент с неравными бинарными коэффициентами диффузии приводит к тому, что элементарный химический состав смеси становится переменным. Это наиболее отчетливо проявляется в многокомпонентных смесях, содержащих компоненты с существенно различными диффузионными свойствами. В уравнениях (25, 26) находит отражение тот факт, что в неизотермических условиях при наличии многокомпонентной диффузии элемент объема газа в потоке является термодинамически открытой системой, обменивающейся частицами с окружающей средой.

Диффузионные (переносные) свойства компонент влияют в основном на распределение полей концентраций химических элементов, из которых состоят компоненты реагирующей смеси, что находит отражение в уравнениях диффузии (сохранения) для этих элементов (10). Уравнения диффузии (сохранения) химических элементов (10), а точнее, их интегралы, используются для замыкания системы уравнений при определении состава многокомпонентной смеси (Иванов и др., 1978; Вихорев, 1981). Отклонение элементарного химического состава многокомпонентной смеси от стехиометрического может привести к изменениям параметров течения и повлиять на интенсивность процессов тепломассопереноса (Иванов и др., 1978).

Первоначально изменение элементарного состава в многокомпонентных газовых смесях изучалось при разработке ракетных двигателей применительно к процессам обогащения смесей определенным элементом смеси. Как и другие кинетические эффекты (термодиффузия, диффузионный термоэффект), диффузионное разделение химических элементов может сыграть существенную роль в условиях неидеальности газовых смесей, когда свойства газа существенным образом зависят от состава (например, газовые смеси, в состав которых входят ионизованные компоненты, смеси при высоких давлениях, а также многокомпонентные химически равновесные газовые смеси). В работах ( Суслов и др. , 1971; Суслов , 1972; Иванов и др. , 1978) показано, что эффект диффузионного разделения химических элементов может оказать существенное влияние на эффективную теплоемкость и теплопроводность многокомпонентных химически равновесных газовых смесей, что может привести к значительному изменению параметров течения и теплоотдачи.

Диффузионное разделение химических элементов может играть важную роль в потоках селективно излучающих и поглощающих высокотемпературных многокомпонентных газов, что важно при оптической диагностике таких сред ( Петухов , 1987).

В общем случае течения многокомпонентных химически реагирующих газовых смесей возникает необходимость аккуратного учета переносных (диффузионных) свойств компонент. Эффект диффузионного разделения химических элементов наиболее существенно проявляется в вязких (ламинарных) многокомпонентных потоках. Что касается многокомпонентных турбулентных течений, где в основной части потока перенос компонент происходит под действием турбулентного перемешивания, то в них диффузионное разделение заметно только в узкой пристеночной области течения (вязкий подслой). Но, так как параметры потока претерпевают наиболее сильные изменения в пристенной области вязкого течения, где имеют место большие градиенты скоростей, температур и концентраций, то диффузионное разделение химических элементов может оказать определенное влияние на интенсивность процессов тепломассообмена при высоких тепловых напряженностях.

• 4.    Течение диссоциирующего азотного тетраксида

  Одной из наиболее изученных и перспективных в термодинамическом отношении систем, представляющих интерес для ядерной энергетики, является диссоциирующий азотный тетраксид ( Красин , 1970; Колыхан, Нестеренко ,  1977; Нестеренко, Тверковкин ,  1980). Основными реакциями,

протекающими в термически диссоциирующем азотном тетраксиде, являются реакции I и II

I                 II

N 2 O 4 + М о 2 NO 2 + М о 2 NO + 0 2 + М,

(3)     (4)

где М - любая частица (молекула N 2 O 4 , NO 2 , NO, 0 2 или частица инертного газа-разбавителя), активирующая молекулы N₂O₄ или NO₂ в прямых реакциях и дезактивирующая ударные комплексы, образующиеся в обратных реакциях.

При данной схеме термической диссоциации (27) получающаяся в результате этих реакций смесь содержит четыре компоненты: N 2 O 4 , NO 2 , NO, 0 2 , и состоит из двух элементов - кислорода О и азота N. В соответствии с формулами (9, 11) по определению можно получить следующие выражения для концентраций химических элементов О и N

*

c O

4 m _O m₁

с 1

2 m

+ ---O С2 +

m2

m O

---сз ⁺

*

cN

2 m N

-----С 1 +

m1

m3

m

2mO с4,

m4

^m N      N

-----С 2 +-- С з .

N

m2

m3

Из этих двух соотношений лишь одно является независимым, так как должно выполняться очевидное равенство

*          *1

c O + c N

Для определения четырех неизвестных массовых концентраций компонент с 1 , с 2 , с 3 , с 4 имеем две константы равновесия Кс I и Кс II , которые могут быть выражены через массовые концентрации компонент

Kei = c2 К ,(31)

Кси = Сз c1/2 /с2,

и условие

С 1 + С 2 + С 3 + С 4 — 1.

Заметим, что условие (33) может быть заменено на эквивалентное условие (30).

При замыкании системы уравнений (31) - (33) для определения состава при равновесном течении реагирующей смеси (27) в качестве недостающего четвертого уравнения при строгой постановке задачи необходимо воспользоваться уравнением диффузии (сохранения) для одного из химических элементов, например, кислорода или азота. При двухслойной модели течения (вязкий подслой -турбулентное ядро потока) (Вихорев, 1981) имеем ck — С*a

- Z c_k i i — 1

1 1 ⁽ c i     ^c iл )

. Sc i )

- в вязком подслое;

c k ^— С * a ^— const

-

в турбулентном ядре потока.

Здесь c iл

-

значение концентрации i -й компоненты на границе: ламинарный (вязкий) подслой

-

турбулентное ядро; c

. *

ka

-

значение концентрации k -го элемента на оси трубы. Уравнения (34) для смеси

(27) принимают вид

c

*

O

— 0,696

-

c1

—

c 2

—

^С2 л ^{) +}

(    1                                (     1

^{+ 0} ,⁵³³ I C_r^-1 l ^{( С}3 - ^С3 л ^{) +} l c ^-1 l^{( С}4 - ^С4 л )   ^;

V S^,   )         V SG )

С N — 0,304 -

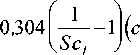
^{- С}1 л ^{) + 0} , 3⁰⁴ ^“-^ j ^{( С}2 - ^С2 л ^{) +}

^{+ 0} , ⁴⁶⁷ I t;     ¹ ] ^{( С}з ^{- С}з л ^{) +} | t; ¹ ] ( ^С4 ^{- С}4 л )

V Sc3   )           V Sc4   )

В турбулентном ядре потока в обычном предположении о равенстве единице всех турбулентных аналогов чисел Шмидта имеем c O — 0,696,

c N — 0,304.

При рассмотрении неравновесных течений смеси (27) при определении состава можно использовать уравнение диффузии (сохранения) элемента (для О или N), равенство (30) и два уравнения неразрывности (диффузии) для компонент - продуктов реакции, например, NO 2 и NO, либо три любые уравнения диффузии для компонент смеси и равенство (33).

Проделанный нами численный анализ ( Вихорев , 1981; Vikhorev , 1997) показал, что при расчете интегральных характеристик течения, таких как числа Нуссельта и Стэнтона, коэффициентов теплоотдачи и сопротивления, для данной реагирующей смеси (27) нет необходимости решать громоздкую систему уравнений для определения состава, а можно довольствоваться более простым и оправданным рассмотрением. В случае малого перекрестного эффекта I и II стадий реакции с достаточной степенью точности для данной реагирующей системы (27) можно считать, что Sc i — const ® 1 ( i — 1,2,3,4) - это эквивалентно предположению о постоянстве элементарного химического состава смеси во всей области течения. При этом для замыкания системы уравнений при определении состава могут быть использованы обычные стехиометрические соотношения химической кинетики. Принятие стехиометрического соотношения между мольными долями компонент NO и O 2 ( Х 3 — 2 Х 4 ) для области вязкого подслоя означает, что не учитывается некоторое различие в их диффузионных свойствах. В большинстве практически важных случаев течений, как показали наши расчеты ( Вихорев , 1981; Vikhorev , 1997), это оправдано, так как для исследуемой смеси (27) с хорошей точностью (0,2 + 0,3%) можно полагать

D 23 ^— D 24 , D 13 ^— D 14 .

По своим молекулярным массам, газокинетическим характеристикам и диффузионным свойствам компоненты NO и О 2 мало отличаются друг от друга. Кроме того, перекрестный эффект первой и второй стадий реакций мал, и имеет место достаточно слабая зависимость свойств смеси от состава. Это позволяет применить для описания течения и теплообмена диссоциирующей смеси (27) квазибинарный подход ( Петухов , 1987).

• 5.    Результаты расчетов. Сопоставление с экспериментальными данными

  В настоящей работе на основе разработанных интегральных методов ( Вихорев, Лапин , 1968, 1969; Вихорев , 1981; Vikhorev , 1997) проведены многочисленные расчеты теплоотдачи и сопротивления трения при турбулентном движении в круглой трубе диссоциирующего (рекомбинирующего) азотного тетраксида (27) в случае установившегося режима течения. При расчетах использовались данные по физико-химическим свойствам смеси (27), наиболее полно приведенные в монографии ( Нестеренко и др. , 1976).

Приведем лишь сопоставления наших расчетных результатов с наиболее надежными экспериментальными данными ( Петухов и др. , 1971; Майданик , 1972). Результаты некоторых наших расчетов, соответствующих условиям различных опытов при равновесном течении ( Петухов и др. , 1971; Майданик , 1972), приведены в табл.1.

Таблица 1.

	р = 1 вх.	12,7 атм;	Р вых . = 8 атм;			G = 38,3 кг/ч
x / d	т w ,	q w -10 —3 ,	Re w -10 — 3	Pr w	т T эксп.,	т T теор.,	St эксn. ■ 10 2	St meop. - 10 2
	K	Вт/м2			К	К
25,6	388,1	219,6	225	0,872	376,5	371	0,1983	0,2120
49,3	389,8	219,9	224	0,878	378,0	372	0,1979	0,2119
93,7	393,1	220,7	218	0,897	381,4	375	0,1972	0,2112
142,7	400,0	221,4	215	0,930	386,1	382	0,1965	0,2101
181,5	403,5	222,0	211	0,955	389,6	383	0,1933	0,2051
256,1	411,1	224,9	206	0,965	394,2	387	0,1934	0,2053
287,8	414,2	225,5	203	0,968	396,7	390	0,1937	0,2061
323,9	419,4	226,2	201	0,955	399,9	393	0,1951	0,2069
	р х = 19 атм;		Р вых . = 18,8 атм			G = 9,91 кг/ч
x / d	Т w ,	q w -10 —3 ,	Re w -10 — 3	Pr w	т T эксп.,	T теор.,	St эксп. ■ 10 2	St meop. - 10 2
	K	Вт/м2			К	К
22,6	469,2	191,2	47,4	0,864	409	398	0,2751	0,2832
71,6	541,1	199,3	42,1	0,721	432	449	0,3077	0,2931
117,0	623,3	206,7	38,1	0,695	463	481	0,3203	0,3013
	Р вх. = 45,6 атм;		Р вых. = 45,2 атм			G = 22,36 кг/ч
x / d	Т w ,	q w -10 —3 ,	Re w -10 — 3	Рг r w	T эксп.,	т T теор.,	St эксп . ■ 10 2	St meop . - 10 2
	K	Вт/м2			К	К
36,1	528,6	436,6	104,8	0,717	440	422	0,2520	0,2397
67,8	579,3	449,2	95,0	0,679	455	441	0,2638	0,2502
103,9	652,7	469,9	84,4	0,671	479	464	0,2721	0,2612

Из табл.1 видно, что по значениям числа Стэнтона и среднемассовым температурам наши расчетные результаты хорошо согласуются с экспериментальными данными в достаточно широком диапазоне изменения температур, давлений и чисел Рейнольдса.

Здесь р вх , , р вых. - давление во входном и выходном сечениях экспериментального участка; G - массовый расход газа через трубу с внутренним диаметром d = 3,09 мм; T w - температура стенки; Re w , Pr w

- числа Рейнольдса и Прандтля, определенные по условиям на стенке; Т _эксп , Т _т - экспериментальные и теоретические (расчетные) значения среднемассовой температуры газа; St_эксп . , St_meop . - экспериментальные и теоретические (расчетные) значения чисел Стэнтона.

В табл.2 приведены сопоставления наших расчетных результатов по теплоотдаче и сопротивлению трения с экспериментальными данными ( Петухов и др. , 1971; Майданик , 1972) для неравновесного режима течения.

Таблица 2.

	Р вх. = 7,2 атм;		Р вых. = 6,0 атм;     Т х = 489,9 К;     Т вых.				= 770,3 К	G = 8,93 кг/ч
x / d	Т w , K	q w -10 —3 , Вт/м2	Re w X 10-3	Pr w	T эксп., К	т 1 теор., К	t эксп. X 10 2	St t теор. X 10 2	^ теор. X 10 2	^ a w X 10 2
25,6	608,3	101,9	33,8	0,704	518,5	520	0,327	0,283	1,91	2,29
49,3	635,9	102,8	32,6	0,701	546,5	552	0,331	0,288	1,93	2,32
93,7	685,2	103,7	30,8	0,694	599,5	605	0,337	0,291	1,98	2,36
142,7	735,9	104,2	29,2	0,690	642,0	655	0,342	0,293	2,01	2,38
181,5	774,0	104,8	28,0	0,685	675,0	690	0,346	0,294	2,03	2,40
256,1	837,2	105,7	26,2	0,688	719,0	727	0,350	0,298	2,07	2,44
287,8	852,2	105,7	25,8	0,690	736,0	740	0,353	0,299	2,08	2,46
323,9	873,6	105,7	25,2	0,693	755,0	761	0,353	0,300	2,09	2,47

Здесь обозначения те же, что и в табл. 1; ^ теор. , ^ „w - теоретические (расчетные) коэффициенты трения и коэффициенты сопротивления трения, определенные для соответствующего течения при постоянных физических свойствах.

Из табл.2 следует, что наши расчетные результаты находятся в хорошем соответствии с экспериментальными данными при выполнении аналогии Рейнольдса между теплопередачей и трением.

• 6.    Заключение

  Рассмотрены основные проблемы конвективного тепломассообмена при внутренних течениях многокомпонентных химически реагирующих газовых смесей. Дано математическое описание течения и тепломассопереноса при химических превращениях. Рассматриваются вопросы определения состава многокомпонентной газовой смеси при использовании уравнений диффузии для отдельных химических элементов. Для расчета процессов многокомпонентной диффузии предлагается методика расчета диффузионных потоков и эффективных коэффициентов диффузии компонент. Проведен анализ кинетического эффекта диффузионного разделения отдельных химических элементов в вязких многокомпонентных газовых смесях, содержащих компоненты с существенно различными диффузионными свойствами. Приведены результаты исследований внутренних течений диссоциирующего азотного тетраксида. Показано, что для описания течения и теплообмена в этом случае можно применить квазибинарный подход. Сопоставления наших расчетных результатов с экспериментальными данными различных авторов ( Петухов и др. , 1971; Майданик , 1972; Колыхан, Нестеренко , 1977; Нестеренко, Тверковкин , 1980), выполненные в широком диапазоне изменения всех параметров течения, свидетельствуют о практической надежности и эффективности предлагаемых методов расчета равновесных и неравновесных течений многокомпонентного химически реагирующего газа.