Научные статьи \ Прикладные науки. Медицина. Технология \ Химическая технология. Химическая промышленность. Родственные отрасли \ Специальные определители для химической технологии

Тепломассоперенос в процессе конвективной сушки тонких плоских влажных материалов

Автор: Ольшанский А.И., Котов А.А.

Журнал: Вестник Витебского государственного технологического университета @vestnik-vstu

Рубрика: Технология и оборудование легкой промышленности и машиностроения

Статья в выпуске: 1 (38), 2020 года.

Бесплатный доступ

Изложена методика расчета конвективной сушки тонких материалов легкой промышленности на основе уравнения кинетики сушки А. В. Лыкова и метода расчета сушки Б. С. Сажина. Приведена обработка экспериментальных данных по сушке шерстяного войлока, натуральной кожи и ткани. Даны уравнения для определения плотностей тепловых потоков, интенсивности испарения влаги, длительности сушки и температуры для периода падающей скорости. Вычислены значения коэффициента теплообмена и числа Био для второго периода сушки. Установлено, что при мягких режимах сушки и незначительных градиентах температуры по сечению тонкого тела число Био принимает значения меньше единицы, и основным лимитирующим фактором при сушке тонких материалов является внешний тепловлагообмен поверхности испарения с окружающей средой. Показано, что относительная скорость сушки определяется только влагосодержанием материала и не зависит от режима сушки. Дано сопоставление расчетных параметров сушки по приведенным формулам с опытными значениями. Несовпадение значений находится в допустимой зоне точности проведения эксперимента.

Еще

Конвективная сушка, скорость сушки, влагосодержание, коэффициент теплопроводности, температура, интенсивность испарения, коэффициент теплообмена, число био

Короткий адрес: https://sciup.org/142224645

IDR: 142224645 | УДК: 66.047.1 | DOI: 10.24411/2079-7958-2020-13808

Текст научной статьи Тепломассоперенос в процессе конвективной сушки тонких плоских влажных материалов

Витебский государственный технологический университет

Кинетикой принято называть изменение среднего влагосодержания и средней температуры материала в процессе сушки. В условиях протекания процесса при мягких режимах сушки весь процесс разделяют на периоды прогрева материала, постоянной скорости сушки (первый период) и падающей скорости (второй период). При сушке тонких материалов период прогрева очень мал по сравнению с длительностью сушки. Период постоянной скорости протекает при постоянной температуре мокрого термометра t_ì . В большинстве случаев сушка при мягких режимах происходит и при постоянной температуре, равной t_ì . Второй период начинается от критического влагосодержания u_êð с возрастанием температуры от t_ì до температуры среды t_ñ при времени сушки τ→ ∞.

Сушка ряда материалов может происходить сразу от начального влагосодержания u₀ в периоде падающей скорости с непрерывным повышением температуры [1–3]. Сушка текстильных материалов после механического отжима также происходит в периоде падающей скорости [1–3]. ПОСТАНОВКА ЗАДАЧИ

Основной задачей кинетики сушки является определение длительности сушки. Аналитический путь решения данной задачи очень сложен и не всегда возможен. В силу этих трудностей необходимо прибегать к экспериментальным исследованиям для разработки приближенных зависимостей для расчета кинетики сушки с минимальным числом постоянных, определяемых опытным путем [1, 3–5]. При этом более эффективными являются такие методы, которые основаны на наиболее общих закономерностях сушки и устойчивых комплексных переменных, характерных для процесса сушки. Выбор теплового режима, размер и тип сушильного аппарата существенно зависят от продолжительности сушки конкретного материала и решением этой задачи определяется эффективность работы установки, расход энергии на сушку и качество высушиваемого материала.

Целью исследования является разработка на основании уравнения кинетики сушки А. В. Лыкова с использованием метода расчета кинетики Б. С. Сажина достаточно простой надежной методики расчета длительности сушки исполь- зуемых в легкой промышленности тонких плоских влажных материалов, таких как натуральная кожа, ткань, войлок.

ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ Основное уравнение кинетики сушки запи шем в виде баланса тепла [1, 6]

Чп ₌]_ПТ ₌ а , М_п ₌ ^^^, (1)

Qi Jrr «кР ^i '

где q_I , q_II – плотности потока тепла в первом и втором периодах сушки; j_I , j_II – интенсивность испарения влаги в первом и втором периодах сушки; r – теплота парообразования; α _êð , α – коэффициенты теплообмена в первом и втором периодах сушки; Δ t_I , Δ t_II – разности температур в периодах сушки:

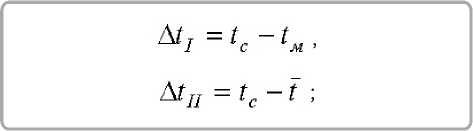
t – среднеинтегральная температура во втором периоде; N * – относительная скорость сушки; Rb – число Ребиндера.

Путем обработки экспериментальных данных по сушке ряда различных материалов установлена обобщенная зависимость [6]

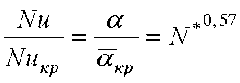
где Nu_êð , Nu – теплообменные критерии Нуссельта в первом и втором периодах сушки.

Уравнение (2) представим в виде

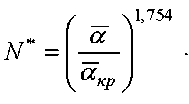
Экспериментальными исследованиями установлено [1, 3, 4, 6], что коэффициенты теплообмена α во втором периоде сушки изменяются с уменьшением влагосодержания материала по эмпирической зависимости [1, 4, 6]

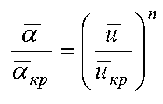
где u и u êð – текущее и критическое влагосодер-жание материала, соответствующее переходу от первого периода сушки ко второму. Постоянная n зависит от вида влажного материала и не зависит от режима сушки.

На основании зависимости (4) и уравнения (1) запишем для тепловых потоков

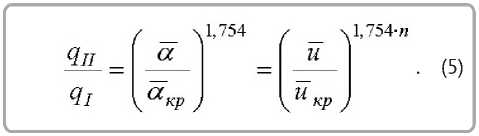
Плотность потока тепла в первом периоде сушки определяется по уравнению оде сушки

;

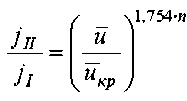
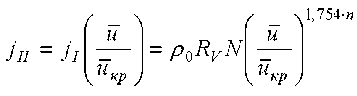
, (8)

где ρ ₀R_VN – интенсивность испарения влаги в первом периоде сушки.

Температуру материала во втором периоде сушки можно определить из уравнения (1). Запишем, при Rb = 0

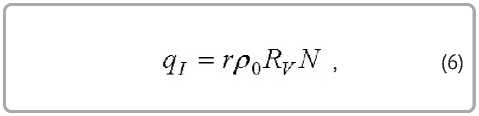
Подставляя N * из уравнения (3), с учетом (4) получим

где ρ ₀ – плотность сухого материала, R_V = V/F = = δ – толщина материала, определяемая как отношение объема тела к площади его поверхности, N – скорость сушки в первом периоде. Тогда из уравнений (5) и (6) плотность потока тепла во втором периоде сушки

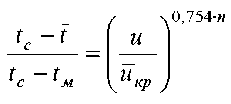
Чи = 4i

_ xl,754-n М

xl,754-я

= rp^RyN —

. (7)

Среднеинтегральная температура во втором периоде сушки

■\

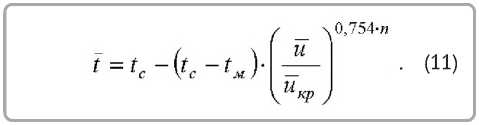
Расход тепла на нагревание тонкого влажного материала значительно меньше расхода тепла на испарение из него влаги ( c_вл• Δ t << r , где c_вл – удельная теплоемкость влажного материала) и для таких тел число Ребиндера Rb << 1 [1, 6, 7].

В реальных условиях сушки тонких материалов при u → u_ð , где u_ð – равновесное влагосо-держание материала, числа Rb ≈ 0,1–0,25. При малых величинах числа Rb его значениями можно пренебречь.

Из уравнения баланса тепла (1) определяется интенсивность испарения влаги во втором пери-

Для материалов, сушка которых происходит в периоде падающей скорости, отношение вла-госодержани й ( u / u _êð ) необходимо заменить на отношение ( u / u₀ ).

Температуру материала во втором периоде можно вычислить по уравнению [7]

i = t_c -(t_c -1_м\ехр(-т_$ -г_л) , (12)

где m_t – темп нагрева.

Длительность сушки во втором периоде τ _II определяется по формуле [3]

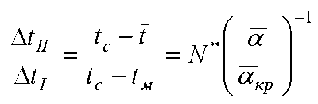
. (9)

TII

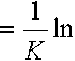
Мкр M р и- и

где K – эффективный коэффициент скорости сушки.

Темп нагрева тонкого влажного материала m_t при малых значениях числа Био Bi < 1 равен [8, 14]

. (13)

с^-Ро 1Rr

Темп нагрева m_t определяется из опыта путем измерения температуры в любой точке тела для двух последовательных моментов времени регулярного режима [7, 8, 14]

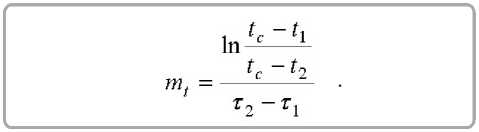
Б. С. Сажиным в основу расчета кинетики сушки положено обобщенное уравнение массо-передачи [4, 9]

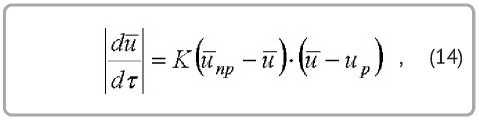
где d u / d τ – скорость сушки; u _ïð – влагосодер-жание, достигаемое материалом в стадии прогревания.

Интегрированием (14) от начального влагосо-держания u₀ с учетом влагосодержания u_ïð получим длительность сушки до любого заданного значения текущего влагосодержания [9]

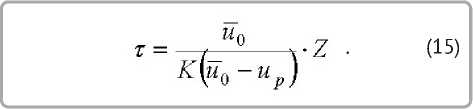
Параметр Z определяется выражением [9]

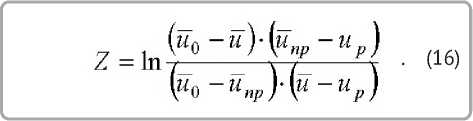
В системе координат Z = f ( τ ) кривые кинетики представляют собой прямые, угол наклона которых определяет скорость сушки K , а отрезки, отсекаемые по оси Z при u = u_ð , равны Z₀ = u _ïð , определяемые по уравнению (15).

На рисунках 1, 2 и 3 изображены кривые сушки u = f ( τ ) и температурная кривая t = f ( τ ) для одного из режимов сушки шерстяного войлока, стелечного полувала (натуральная кожа) и тонкой ткани. Кривые сушки для кожи и ткани взяты из [10, 11]. Значения режимов сушки соответствуют обозначениям, приведенным в таблице 1.

Обработка кривых кинетики сушки Z = f ( τ ), представленных на рисунках 1, 2 и 3 ( б ), дает простое уравнение длительности процесса сушки

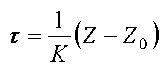
Величина Z₀ определяется по (15) при значении u = u_ïð .

Скорость сушки влажного материала d u / d τ в общем случае определяется двумя механизмами переноса: механизмом тепломассообмена между поверхностью испарения тела и внешней средой (внешний перенос) и механизмом тепло-массопереноса внутри самого тела (внутренний перенос) [4, 9, 12].

При низкой интенсивности внешнего теплов-лагообмена при сушке тонких материалов при малых градиентах температуры теплообменный критерий Bi << 1. Лимитирующим фактором, определяющим интенсивность тепловлагообме-на, является взаимодействие поверхности испарения с внешней средой [4, 7, 9]. При этом в реальных условиях сушки тепловлагообменные критерии Bi и Bi_m оказываются приблизительно одинаковыми [13]. В этих условиях внутренний перенос слабо влияет на скорость сушки [4, 8, 14].

В результате обработки большого числа экспериментальных данных по сушке различных материалов была получена формула для теплообменного критерия Нуссельта [1, 6, 7, 15]

Таблица 1 – Режимные параметры конвективной сушки войлока, стелечного полувала и шерстяной ткани
Показатели Режимы	t_c , °C	υ , м/с	ф , %	^ир	Ч , ° C	u_KB^р	N^10-³ , с¹
Шерстяной войлок (рисунок 1)
1	90	5	5	0,02	38	0,75	0,84
2	120	3	5	0,02	40	0,75	1,03
3	120	5	5	0,01	42	0,72	1,22
Стелечный полувал (рисунок 2)
1	40	1	60	0,16	33	0,66	0,095
2	60	1	45	0,145	36	0,8	0,118
3	40	1	40	0,15	35	0,65	0,19
Шерстяная тонкая ткань (рисунок 3)
1	90	5,3	6	0,02	40	—	11,2
2	90	2,8	5	0,015	39	—	9,5
3	87	0,9	4	0,062	35	—	5,5
4	63	5,6	25	0,04	39	—	6,5
⁵	50	5,6	30	0,045	30	—	4,5

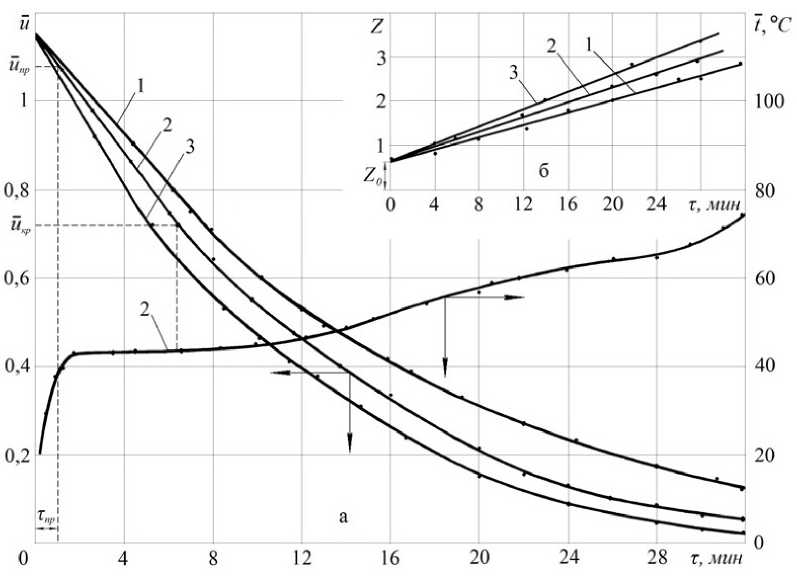
Рисунок 1 - Кривые сушки U = f ( т ) и температурная кривая t = f ( т ) для режима сушки № 2 в процессе конвективной сушки шерстяного войлока (а) и зависимость параметра Z = f (т) (б). Режимы сушки указаны в таблице 1

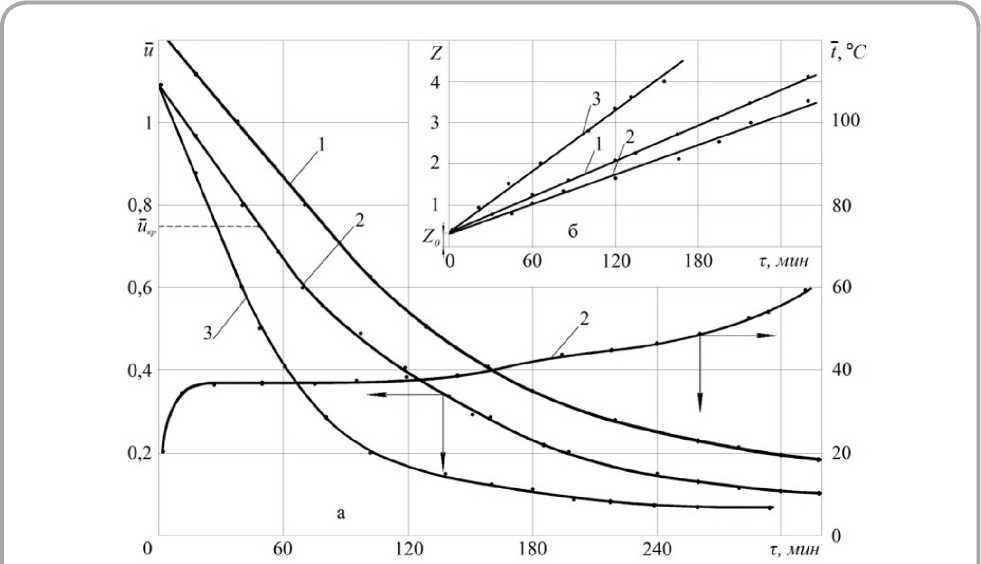
Рисунок 2 – Кривые сушки u = f ( τ ) и температурная кривая t = f ( τ ) для режима сушки № 2 в процессе конвективной сушки стелечного полувала (а) и зависимость параметра Z = f ( τ ) (б). Режимы сушки указаны в таблице 1

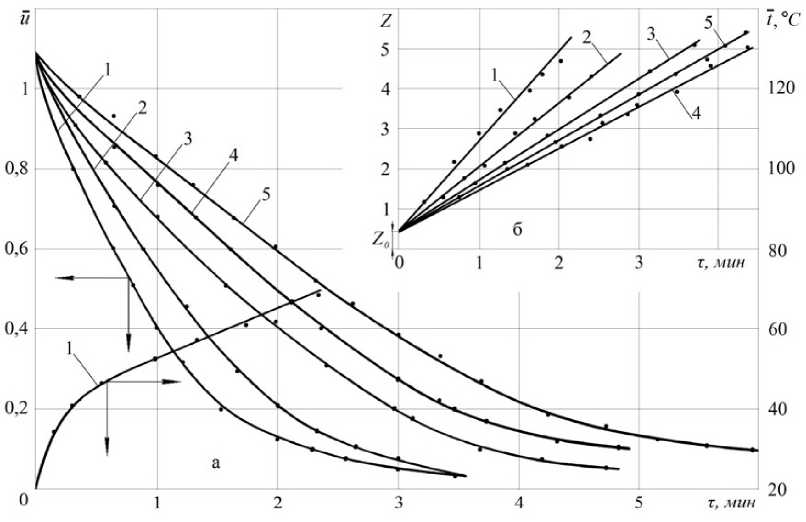
Рисунок 3 – Кривые сушки u = f ( τ ) и температурная кривая t = f ( τ ) для режима сушки № 1 в процессе конвективной сушки ткани (а) и зависимость параметра Z = f ( τ ) (б). Режимы сушки указаны в таблице 1

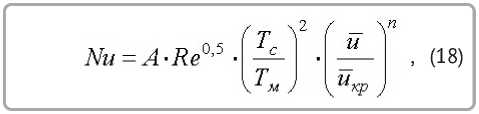
где Nu и Re – критерии Нуссельта и Рейнольдса; T_ñ , T_ì – абсолютные температуры среды и мокрого термометра.

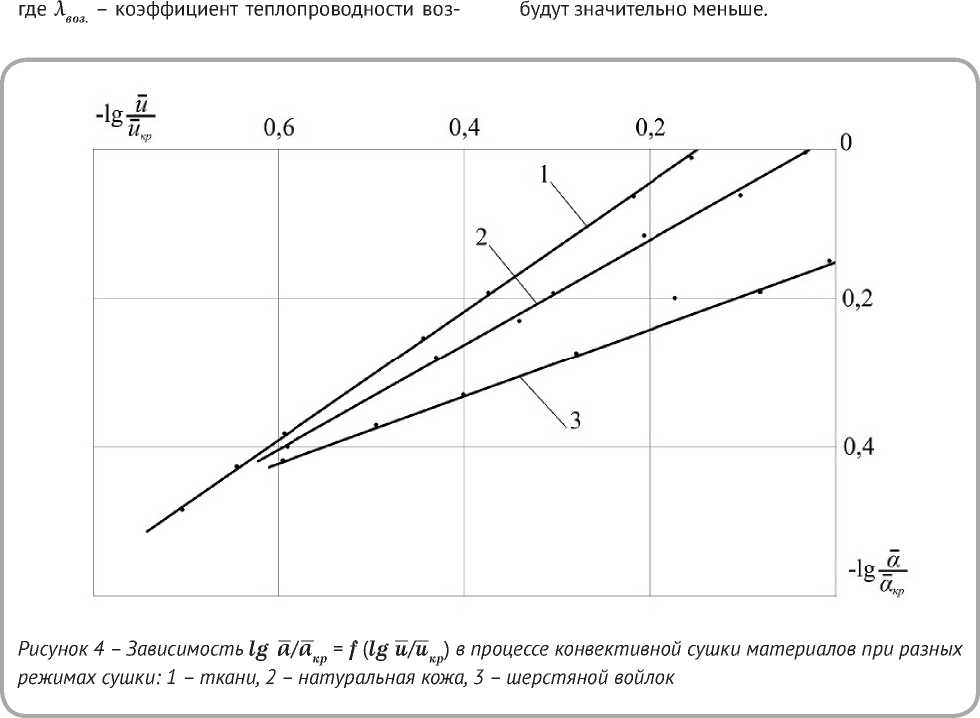
Установлены значения коэффициента A и постоянной n в уравнении (18) [1, 6, 14, 15]: для шерстяного войлока A = 0,435, n = 0,5; для натуральной кожи A = 0,9, n = 0,65; для тканей A = 0,89, n = 0,42.

На рисунке 4 представлены зависимости lg α / α _êð = f ( lg u / u_êð ) для конвективной сушки тканей, натуральной кожи и шерстяного войлока [1, 6, 15].

Значения коэффициента теплообмена α , вычисленные по уравнению (18) и критерию Нуссельта

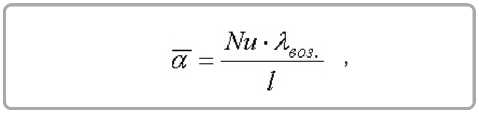
духа; l – длина образца материала по направлению потока воздуха, даны в таблице 2.

Число Био

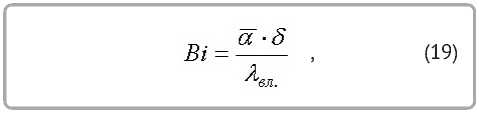
где λ _вл. – коэффициент теплопроводности влажного материала. За определяющий размер влажного тела принимается толщина материала δ . Значения числа Bi , вычисленные по (19), приведены в таблице 2.

Следует отметить, что в решениях дифференциальных уравнений тепломассопереноса для неограниченной пластины в краевых условиях третьего рода (сушка) за определяющий размер принимается половина толщины пластины, а начало координат помещается в центральной плоскости пластины. Следовательно, значения

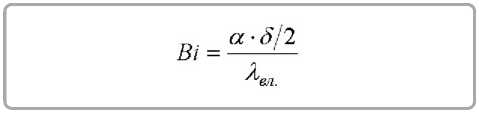
Таблица 2 – Численные значения параметров кинетики конвективной сушки войлока, стелечного полувала, ткани и сопоставление полученных данных с экспериментом
u	α , Вт/м²•град (18)	λ , вл. Вт/м•град (20)	Bi (19)	q, Вт/м²(7)	j II •10³, кг/м²•с (8)	τ , мин ýêñ.	τ , мин (15)	τ _II, мин ýêñ.	τ _II, мин (13)	t, °C ýêñ.	t, °C (11)	t, °C (12)
Шерстяной войлок, пластина 200×150×6 ìì ; ρ ₀ = 160 кг/м³ ; λ ₀ = 0,052 Вт/м•град . Режим сушки: t_ñ = 120 °C ; υ = 3 м/с ; φ = 5 % ; u ₀ = 1,14; u _êð = 0,75; N = 0,96 • 10^-3 ñ^-1 ; t_ì = 42 °C ; α _êð = 30,2 Вт/м²•град ; τ _I = 6 мин ; q_I = 2210 Вт/м² ; j_I =0,92 • 10^-3 кг/м²•с ; m_t = 0,022 мин^-1 ; K = 0,014 мин^-1 (режим сушки № 2)
0,7	29,2	0,278	0,64	2080	0,866	6,5	6,3	1,0	0,92	44	45	44,0
0,6	26,7	0,237	0,67	1817	0,756	8,2	8,2	2,5	2,9	45	45,5	46,4
0,5	23,6	0,212	0,66	1549	0,644	11,0	10,6	5,0	5,2	48	49	50,0
0,4	17,8	0,176	0,62	1273	0,531	14,0	13,5	8,0	8,2	50	52	52,5
0,3	12,6	0,142	0,59	989	0,412	17,0	17,2	11,5	11,9	57	58	60,5
0,2	10,7	0,114	0,61	694	0,288	21,5	22,4	16,5	17,2	62	63	64,5
0,1	8,6	0,084	0,63	378	0,157	29,5	31,3	20,5	23,5	64	65	68,0
Стелечный полувал, пластина 200×150×2,8 ìì ; ρ ₀ = 585 кг/м³ ; λ ₀ = 0,121 Вт/м•град . Режим сушки: t_ñ = 60 °C ; υ = 1 м/с ; φ = 60 % ; u ₀ = 1,34; u _êð = 0,8; u _ð = 0,145; N = 0,12 • 10^-3 ñ^-1 ; t_ì = 35 °C ; α _êðВт/м²•град ; q_I = 473 Вт/м² ; j_I =0,197 • 10^-3 кг/м²•с ; m_t = 1,145 • 10^-3 мин^-1 ; K = 0,025 мин^-1 (режим сушки № 2)												= 18,8
0,7	16,8	0,227	0,21	407	0,17	57	58	17	16,3	36	36,5	35,6
0,6	15,6	0,196	0,192	341	0,14	68	69	28	29,5	37	37,0	36,5
0,5	13,2	0,192	0,20	277	0,11	92	94	52	51,1	38	37,5	37,6
0,4	11,2	0,165	0,185	216	0,09	120	121	81	78,8	39	38,5	38,3
0,3	9,5	0,154	0,177	155	0,06	158	159	119	120	40	39,5	39,2
0,25	8,3	0,147	0,158	126	0,05	178	180	145	152	41	41,5	40,6
Шерстяная ткань, толщина δ = 0,4 • 10^-3 ì ; ρ ₀ = 100 кг/м³ ; λ ₀ = 0,046 Вт/м•град . Режим сушки: t_ñ = 90,5 °C ; υ = 5,3 м/с ; φ = 6 % ; u ₀ = 1,1; u _êð = 1,1; u _ð = 0,025; N = 11,2 • 10^-3 ñ^-1 ; t_ì = 40 °C ; α _макс = 25,3 Вт/м²•град ; q_I = 1075 Вт/м² ; j_I =0,45 • 10^-3 кг/м²•с ; m_t = 3,5 • 10^-3 мин^-1 ; K = 2,52 мин^-1 (режим сушки № 1)
0,8	18,4	0,238	0,031	860	0,35	0,35	0,37	—	—	40	42	43,0
0,7	16,2	0,214	0,030	770	0,33	0,50	0,52	—	—	45	44	45,8
0,6	14,8	0,190	0,029	688	0,29	0,67	0,68	—	—	47	46	46,2
0,5	13,6	0,167	0,028	602	0,26	0,83	0,84	—	—	50	48	48,7
0,4	11,8	0,142	0,027	510	0,22	1,00	1,00	—	—	51	50	49,4
0,3	8,7	0,119	0,024	413	0,18	1,27	1,30	—	—	54	54	52,6
0,2	6,8	0,096	0,021	310	0,13	1,60	1,63	—	—	56	57	55,7
0,1	5,3	0,072	0,018	184	0,08	2,43	2,37	—	—	65	62	61,5

В процессах термической обработки и тепломассообменных процессах сушки важное значение приобретают исследования по изучению изменения коэффициента теплопроводности в зависимости от влагосодержания и температуры. Установлено, что в общем случае с повыше- нием температуры и влагосодержания материалов коэффициент теплопроводности возрастает [1, 4, 8, 16].

Основным требованием для получения более точных значений Хвл является кратковременность теплового воздействия на влажный мате- риал в эксперименте [8].

В результате изучения и анализа ряда источников [8, 11, 14, 16–19] с возможной точностью уст а новлены закономерности изменения λ _вл. = f ( t , u ) для исследуемых материалов. При обработке опытных данных за основу была принята формула В. И. Дубницкого [1, 8].

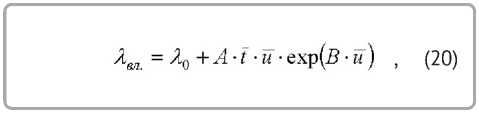
где λ ₀ – коэффициент теплопроводности сухого материала.

В результате установлены приближенные за-

Таблица 3 – Значение параметра Z по формуле (16) и сравнение длительности сушки по уравнению (15) с экспериментом в процессах сушки войлока, натуральной кожи и ткани

u Z (16) τ, мин (15) τ, мин ýêñ. Z (16) τ, мин (15) τ, мин ýêñ. Z (16) τ, мин (15) τ, мин ýêñ. Шерстяной войлок, пластина 200×150×6 ìì Режим сушки № 1 u ïð = 1,0; K = 0,13 мин-1 Режим сушки № 2 u ïð = 0,99; K = 0,14 мин-1 Режим сушки № 3 u ïð = 0,98; K = 0,096 мин-1 0,6 1,35 10,0 10,5 1,20 8,2 8,2 1,17 12,3 12 0,5 1,57 12.2 12,0 1,57 11,3 11,0 1,45 15,2 15 0,4 2,23 17,2 17,0 2,00 14,5 14,0 1,84 19,4 19 0,3 2,75 21,2 20,5 2,40 17,2 17,0 2,33 24,6 24 0,2 3,39 26,1 26,0 3,00 22,4 21,5 3,15 32,8 31 0,1 4,62 35,6 35,5 4,43 31,3 29,5 3,46 36,3 34 Натуральная кожа – стелечный полувал, пластина 200×150×2,8 ìì Режим сушки № 1 u ïð = 1,04; K = 0,22 мин-1 Режим сушки № 2 u ïð = 0,995; K = 0,025 мин-1 Режим сушки № 3 u ïð = 1,03; K = 0,034 мин-1 0,9 1,06 55,2 53 0,72 33,0 32 0,56 18,9 18 0,7 1,73 90,5 90 1,25 57,3 57 1,05 35,5 35 0,6 2,20 114,6 112 1,49 68,4 68 1,26 42,5 42 0,5 2,62 137,0 136 2,00 91,6 92 1,60 53,6 50 0,4 3,18 165,8 165 2,68 122,7 120 1,81 61,9 60 0,3 3,85 201,0 202 3,46 158,5 158 2,42 81,6 80 0,25 4,70 245,3 243 3,92 180,5 178 2,75 92,8 92 Тонкая шерстяная ткань, толщина δ = 0,4•10-3 ì; ρ0 = 100 кг/м3 Режим сушки № 1 u ïð = 1,05; K = 2,52 мин-1 Режим сушки № 2 u ïð = 1,04; K = 1,68 мин-1 Режим сушки № 3 u ïð = 1,02; K = 1,56 мин-1 0,8 0,85 0,362 0,350 0,84 0,510 0,500 0,99 0,648 0,667 0,7 1,19 0,507 0,500 1,12 0,680 0,667 1,55 1,013 1,000 0,6 1,62 0,688 0,667 1,55 0,942 0,933 2,13 1,390 1,333 0,5 1,97 0,837 0,833 1,95 1,182 1,167 2,53 1,663 1,633 0,4 2,39 1,013 1,000 2,27 1,378 1,367 3,13 2,045 2,000 0,3 3,05 1,297 1,267 2,77 1,682 1,667 3,90 2,547 2,500 0,2 3,87 1,645 1,633 3,46 2,097 2,067 4,60 3,017 3,000 0,1 5,54 2,388 2,433 4,52 2,742 2,700 6,00 3,917 3,883 J висимости Хвл = f (t, й) для войлока, кожи и тканей.

Для шерстяного войлока

/1^ = 0,053 + 2,7-10 ³ • t • и • ехр(- 2 • и ) Вт/м град

Для натуральной кожи

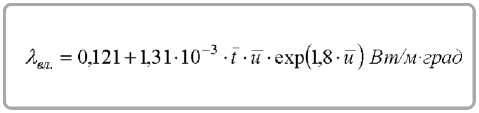
Влияние температуры и влажности тканей на

Х вл = f ( t й ) хорошо изучено [5,16].

Для шерстяных тканей

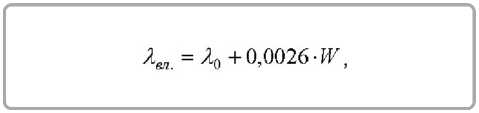
для хлопчатобумажных тканей

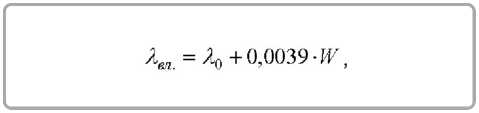
где Х ₀ = 0,046 Вт/мтрад - теплопроводность сухих тканей; W - влагосодержание ткани, % .

Влиянием температуры на изменение λ _вл. в пределах до 80 °C можно пренебречь [16].

Результаты расчетов кинетики сушки по полученным уравнениям для процессов сушки исследуемых материалов представлены в таблицах 2 и 3 и дано сопоставление расчетных значений с экспериментальными. Погрешность в разбросе значений параметров находится в пределах точности обработки опытных данных. ЗАКЛЮЧЕНИЕ

Основное уравнение кинетики сушки А. В. Лыкова совместно с методом расчета кинетики Б. С. Сажина позволяет полностью определить все основные кинетические характеристики тепловлагообмена. Значения параметров, вычисленные по формулам, хорошо согласуются с экспериментом.

Использование полученных уравнений в инженерной практике позволит значительно сократить число трудоемких и сложных экспериментов и объем расчетной работы при обработке опытных данных, необходимых для обоснованного и правильного выбора сушильного оборудования.

Список литературы Тепломассоперенос в процессе конвективной сушки тонких плоских влажных материалов

Лыков, А. В. (1968), Теория сушки, Москва, 472 с.
Натареев, О. С., Кокина, Н. Р., Натареев, С. В. (2015), Теплоперенос в процессе конвективной сушки влажного материала, Известия вузов, Химия и химическая технология, 2015, No 2, С. 65-70.
Рудобашта, С. П. (2015), Теплотехника, Москва, 672 с.
Акулич, П. В. (2010), Расчеты сушильных и теплообменных установок, Минск, 443 с.
Балыхин, М. Г., Разумеев, К. Э., Кошелева, М. К., Захарова, А. А. (2015), Процессы сушки и термовлажностной обработки в текстильной и легкой промышленности, Актуальные проблемы сушки и термовлажностной обработки материалов в различных отраслях промышленности и агропромышленном комплексе, Сборник научных статей Первых Международных Лыковских научных чтений, Москва, 2015, С. 193-20
Лыков, А. В., Куц, П. С., Ольшанский, А. И. (1972), Кинетика теплообмена в процессе сушки влажных материалов, Инженерно - физический журнал, 1972, Т. 23, No 3, С. 401-406.
Ольшанский, А. И., Гусаров, А. М. (2017), Экспериментальное исследование кинетики сушки тонких, плоских влажных материалов методом регулярного режима с использованием обобщенных комплексных переменных, Инженерно - физический журнал, 2017, Т. 90, No 3, С. 700-713.
Васильев, В. Н., Куцакова, В. Е., фролов, С. В. (2013), Технология сушки. Основы тепло- и массопереноса, Санкт - Петербург, 224 с.
Сажин, Б. С., Сажин, В. Б. (1997), Научные основы техники сушки, Москва, 447 с.
Филоненко, Г. К., Лебедев, П. Д. (1952), Сушильные установки, Москва - Ленинград, 262 с.
Лыков, А. В. (1938), Кинетика и динамика процессов сушки и увлажнения, Москва, 776 с.
Кошелева, М. К., Рудобашта, С. П. (2015), Особенности процесса сушки нетканых текстильных материалов, Актуальные проблемы сушки и термовлажностной обработки материалов в различных отраслях промышленности и агропромышленном комплексе, Сборник научныхстатей Первых Международных Лыковскихнаучных чтений, Москва, 2015, С. 205-210.
Лыков, А. В., Михайлов, Ю. А. (1963), Теория тепло- и массопереноса, Москва - Ленинград, 536 с.
Кавказов, Ю. Л. (1973), Тепло- и массообмен в технологии кожи и обуви, Москва, 272 с.
Ольшанский, А. И., Климентьев, А. Л., Петренко, В. В. (2018), Исследование кинетики конвективной сушки натуральных кож, Вестник Витебского государственного технологического университета, 2018, No 1 (34), С. 49-62.
Колесников, П. А. (1965), Теплозащитные свойства одежды, Москва, 345 с.
Франчук, А. У. (1969), Таблицы теплотехнических показателей строительных материалов, Москва, 143 с.
Григорьев, И. С. (1991), Физические величины.Справочник, Москва, 1232 с.
Блэзи, В. (2012), Справочник проектировщика.Строительная физика, Москва, 616 c.

Еще