Теплообмен при течении вязкоупругой жидкости в аппарате с турбинной мешалкой

турбинная мешалка Раштона, представляющая собой мешалку с прямыми лопатками, расположенными радиально [1]. Лопатки могут быть приварены к диску или прикреплены с помощью болтов (рис. 1).

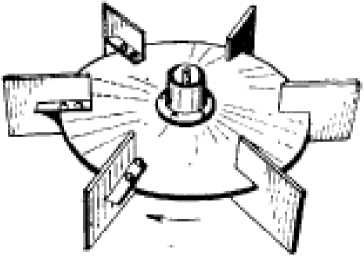
Рис. 1. Турбинная мешалка

В данной работе проведено численное моделирование неизотермического ламинарного течения несжимаемой неньютоновской жидкости, описываемой реологической моделью вязкоупругой Олдройд-Б жидкости, в аппарате с турбинной мешалкой Раштона. Исходными уравнениями, описывающими неизотермическое течение жидкости в аппарате, будут уравнения движения, энергии и неразрывности в виде [4]

— (p v ) + V-p vv = F + V- ( - pI + o ) , d t

ет

— + v -V T = a V ² T , d t

V- v = 0,

где ρ – плотность жидкости, р – давление, σ – тензор-девиатор напряжений, I – единичный тензор.

Реологическая модель вязкоупругой Олд-ройд-Б жидкости записывается в виде соотношения [5]

v      /         v g + X]G = 2n| D + Х2D где п — сдвиговая вязкость, Х1 - время релаксации, Х2 - время ретардации, а тензор скоростей деформаций определяется как

С учетом (5) уравнение движения (1) примет вид

— (рv)+V-(pvv -nVv) = d г '

= F -V p + V- ( t — 2 0ц D ) .     ^

Граничные условия на свободной поверхности жидкости включают в себя кинематическое и динамическое условия. Кинематическое условие

D = 1 [ V v + ( V v ) ^T ] .

d h    d h

— = - и --+ w ,

5 1      d r

Соотношение (4) содержит также верхнюю конвективную производную, определяемую в виде [5]

g =--+ v -Vg — (Vv )T - g - g - Vv, dt               v ’                 , где верхний индекс Т обозначает операцию транспонирования.

Введем подвижную, связанную с вращающейся мешалкой, цилиндрическую систему координат r , ф,z . Проекции вектора скорости обозначим соответственно через u,v,w. Проекции объемной силы в подвижной системе координат содержат ускорение Кориолиса и центробежное ускорение, а также ускорение силы тяжести и имеют вид

F_r = р ( ю ² r + 2 ю v ) ,

Fv  -2рИ1 ,  Fz = -Р g.

Для решения системы уравнений (1) - (4) используем метод расщепления напряжений [6, 7], согласно которому тензор напряжений расщепляется на вязкоупругую составляющую и вязкую составляющую с помощью равенства g = t + 2ц2 D,

где вязкоупругая составляющая тензора напряжений т удовлетворяет уравнению

V t + Xj т = 2рD.

В формулах (5) и (6) постоянные п 1 и п 2 , представляющие собой соответственно неньютоновский и ньютоновский вклады в общую вязкость, определяются соотношениями

П = П1 +П2, х2 =(i-р)пХ1,  p=3l.

П где h - высота свободной поверхности над мешалкой, свидетельствует о том, что скорость движения свободной поверхности в направлении нормали к ней совпадает с нормальной составляющей скорости движения жидкости [8]. Динамическое условие является условием равенства сил, действующих на свободную поверхность [9]. Будем предполагать, что силы поверхностного натяжения незначительны, так как радиус кривизны поверхности жидкости в аппарате достаточно велик. Тогда динамическое условие может быть записано в виде n -(- pI + g) = - роп1 -1,

где ро - атмосферное давление, а вектор нормали к свободной поверхности жидкости v J dh      [_ n = ^--; 0;1 >.

Id r

Граничные условия для составляющих скорости на твердых стенках заключаются в отсутствии относительного движения жидкости и твердой поверхности. Тогда на дне и боковой стенке аппарата и = 0, v = -ю r, w = 0, а на поверхности вала и мешалки соответственно и = 0, v = 0, w = 0, где го - угловая скорость вращения вала и мешалки.

На оси вращения потока под мешалкой примем

Sw и = 0, v = 0,  — = 0.

d r

Будем предполагать процесс теплообмена в аппарате установившимся. Пусть боковая цилиндрическая стенка аппарата оборудована наружными нагревательными элементами, поддерживающими постоянную температуру T1. Тогда на боковой стенке аппарата будет справедливо граничное условие T=T1. На свободной поверхности жидкости и на дне аппарата примем T=T0, где T0 – температура окружающей среды. На поверхности вала и мешалки примем адиабатическое условие ∂T/∂n=0. Поскольку форма свободной поверхности жидкости неизвестна и должна быть найдена в результате расчетов, то перейдем от физической области течения к расчетной области с известными границами. Для этого физическую область поделим на две подобласти, нижнюю и верхнюю, горизонтальным сечением, проведенным через верхнюю поверхность мешалки. Введем безразмерные координаты и функции

В расчетной области уравнение движения (7) в проекциях на оси координат может быть записано в виде обобщенного уравнения переноса

А(лф ) ₊ -L- A d t           y h i h₂h₃ d Xk

( hh^

л Ukф

I   h k

Af h i h 2 h 3 p»®) hhjh d x, I h, ² d x, . 123    k    k       k

где приняты следующие обозначения:

h = 1, h₂ = r * , h₃ = 1,

*** X j = r , x₂ = ф , x₃ = z , щ = U, u₂ = V, u₃ = W,

Г = 1; Л = л Re,

t ^*

Ut

L ^,

r

*

r

-, ф =ф ,

z

— * v

z

= \ L z

—

H — b h

при z <  H + b

, при z > H+b

—

v

U ^,

* ^p

^{L (} P ^— P о ) n U ’

* L ° _A T — T o = , и = .

n U     T — T 0

где H – высота расположения мешалки над дном аппарата; b – высота лопасти мешалки, а в качестве характерной длины L и характерной скорости потока U выберем соответственно диаметр мешалки d и окружную скорость (в неподвижной системе координат) конца лопасти. Заметим, что свободной поверхности жидкости соответствует при этом значение z^*=1.

После преобразования координат уравнение неразрывности (3) сохранит вид

V- V = 0.

При этом проекции вектора скорости в расчетной области будут определяться следующим образом:

T T       * TZ       * TT7 *     * * ^dy

U = y u , V = y v , W = w — u z —- , d r *

где γ =1 для нижней подобласти и γ=h^* для верхней подобласти; h^*=h/d, а u^*,v^*,w^* – компоненты вектора скорости в безразмерной физической области, определяемой преобразованием

*r       *            *z r = -, ф =ф, z =~. dd

где k – индекс суммирования; Re=ρ nd ²/η – центробежное число Рейнольдса ; n – число оборотов мешалки в единицу времени, а S Φ – член типа источника, который определяется соответственно искомой функции Φ.

Уравнение (6) в расчетной области в проекциях на оси координат также может быть представлено в виде обобщенного уравнения (10). При этом следует считать Γ=0; Λ= We ; We=λ 1 ω – число Вайссенберга. Уравнение (2) в безразмерной форме также приводится к виду (10), где Γ=1; Λ=πRePr; Pr=μ/(ρ a ) – число Прандтля ; a – коэффициент температуропроводности.

Численное моделирование неизотермического течения проведем методом контрольных объемов [10], одним из основных достоинств которого является то, что он обладает консервативными свойствами, то есть обеспечивает интегральное выполнение законов сохранения для всей расчетной области. Поделим расчетную область на контрольные объемы (ячейки) таким образом, чтобы каждая узловая точка содержалась в отдельной ячейке. При этом грани контрольных объемов расположим посередине между соседними узловыми точками. Размещение всех узловых функций в одних и тех же точках приводит к рассогласованию полей скорости и давления. Поэтому выберем разнесенную шахматную сетку [11], в которой точки, где вычисляются компоненты скорости, смещены на полшага в соответствующих направлениях относительно основных точек, в которых вычисляются давление, компоненты тензора напряжений и температура.

Проинтегрируем уравнение (10) по контрольному объему и временному интервалу Δ t^* . В результате, с учетом уравнения неразрывности, получим соотношение, связывающее значения искомой функции Φ в узловой точке P с ее значениями в центрах E, W, N, S, T, B соседних ячеек, в виде

a p ^Ф p = a E ^Ф E + a w ^Ф W + ^a N ^Ф N +

+ a ,Ф, + a_T Ф, + a „Ф„ + S_P A V ,

SS  TT  BB  P

где S_P - узловое значение источникового члена; А V - объем ячейки.

Для расчета формы свободной поверхности жидкости воспользуемся методикой, предложенной ранее применительно к лопастной мешалке в работах [12, 13] и основанной на использовании динамического условия (9) в проекции на нормаль

5 h

° zz - Р ⁺ Р 0 - ² ° rz^ ⁺

5 r

где V 0 - объем жидкости над мешалкой с невозмущенной свободной поверхностью; V ^{( к} ) - объем жидкости над мешалкой на к- ой итерации, который вычислялся на каждой итерации путем ** ( к ) численного интегрирования по значениям h_i   .

Следует отметить, что в соответствии с формулой (16) поправка § h ^{( к} ) не влияет на форму свободной поверхности, а лишь корректирует ее по высоте. Окончательно с учетом поправки § h ^{( к} ) скорректированные значения высоты свободной поверхности h i ^{( к} ) могут быть найдены как

h * ^{( к} ) = h ,"^{( к} ) +5 h ^{( к} ) ,

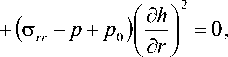
где o rr , o_zz, o_rz - компоненты тензора напряжений.

Будем полагать, что краевые углы смачивания вала и боковой стенки аппарата прямые. Это позволяет считать, что в любой момент вре-

мени в непосредственной близости от вала и

стенки будут справедливы равенства

7*1*   * \   , * / *   *    А * 1

h ( t , r s ) = h ( t , r s +A r ) ,

,*/ * „*1   7*/ *        A *A h (t ,R ) = h (t ,R -Ar ),

где r s - радиус вала; R - радиус аппарата.

Перепишем условие (12) в безразмерном виде

5 h *

5 r *

*        *       *        * Al ^{5 h}

^zz ^- Р + ( ^ rr ^- p ) l —T

(5 r

2 ^

Расчет поля течения проводился на основе алгоритма SIMPLE [10], в котором используется дискретизация уравнений по методу контрольных объемов на сетках с расположением узлов в шахматном порядке.В алгоритме SIMPLE должно задаваться начальное предполагаемое поле давления. Это поле давления в соответствии с рекомендациями [10] полагалось равным p =0 для того, чтобы погрешности округления при расчете градиентов давления не достигали слишком больших значений.

Вначале по уравнениям (10) вычислялись компоненты тензора напряжений и предварительные значения компонент u ,v ,w вектора скорости, не удовлетворяющие уравнению неразрывности. С учетом приближенного решения для скорости находилась поправка к давлению dp из уравнения

a_P 5 p_P = a_E 5 p_E + a_W 5 p_W + a N 5 p_N +

Решение уравнения (15) проводилось на каждой итерации методом Рунге-Кутта [14] при *         *   *         *     *          *

начальном условии h0 = h (t -At , rs + Ar ) с учетом условий (13) и (14) при фиксированном значении производной дh /дr в правой части (15), взятом с предыдущей итерации. При вычисленных на к-ой итерации значениях высоты свободной поверхности hi 'к) может не выполняться условие постоянства объема жидкости в аппарате (при этом достаточно учитывать объем жидкости над мешалкой). Таким образом, возникает необходимость введения некоторой поправки §h(к) к значениям hi. (к) на каждом итерационном шаге. Эта поправка находилась из соотношения vo - v (k) = „(r *2 - r;2 )§h(к),

+ a_s 5 p_s + a_T 5 p_T + a_B 5 p_B + b_p ,

полученного из дискретного аналога уравнения неразрывности с использованием уравнений количества движения.

Затем с учетом поправок δp рассчитывались скорректированные значения компонент скорости на гранях e, w, n, s, t, b ячеек, удовлетворяющие уравнению неразрывности, по поправочным формулам, температуры и давления

*        *»

p = p +a5p , где a - параметр релаксации. В расчетах принималось a=0,8.

Форма свободной поверхности жидкости, соответствующая рассчитанному полю течения определялась в конце каждой итерации. При

*(0)™ этом в качестве начальных значений hi  при нималось значение, соответствующее положению невозмущенной поверхности жидкости.

Дискретные уравнения (11) и (18) решались методом прогонки [15]. В качестве критерия сходимости рассматривалась сумма модулей невязок по всем контрольным объемам при решении уравнений (11). Расчеты проводились по этому критерию с точностью до 10-6 на равномерной сетке. В расчетах принималось

H = D ;   d / D = 0,3; d / D = 0,05;

b/d=0,2; H/H =0,4, где D – диаметр аппарата; H0 – высота невозмущенной поверхности жидкости над дном аппарата; ds – диаметр вала.

На рис. 2 представлена картина линий тока жидкости в меридиональном сечении аппарата. Линии тока характеризуют вторичное циркуляционное течение, которое накладывается на основное окружное течение. Наблюдаются два потока радиально-осевой циркуляции, способствующих перемешиванию жидкости и расположенных соответственно сверху и снизу от мешалки. Фактически осевые потоки жидкости разрываются мешалкой, которая делит область перемешивания на две отдельные зоны.

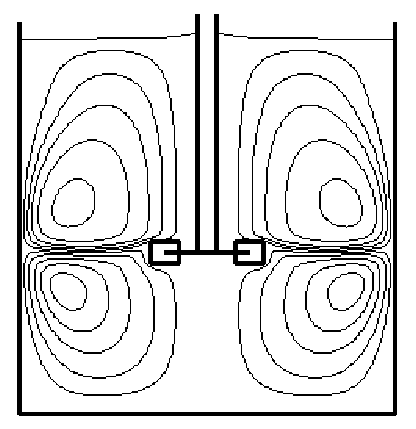
Рис. 2. Радиально-осевая циркуляция в аппарате при Re = 200, We = 5

При перемешивании вязких жидкостей вращательное движение объема жидкости в аппарате приводит к понижению уровня жидкости у вала мешалки и образованию воронки. Однако при перемешивании неньютоновской жидкости, обладающей упругими свойствами, наоборот, наблюдается некоторое повышение уровня жидкости у вала. Это явление связано с наличием в вязкоупругих жидкостях эффекта Вайссенберга, основанного на возникновении нормальных напряжений при сдвиговом течении жидкости. Нормальные напряжения приводят к тому, что жидкость выдавливается из аппарата и поднимается вдоль вала, создавая эффект поднятия. На рис. 3, 4 представлены результаты расчетов изотерм θ=const в меридиональном сечении аппарата.

При небольших значениях числа Рейнольдса конвективный перенос теплоты в направлении от боковой стенки в центральную часть аппарата незначителен и формирование температурного поля определяется в основном теплопроводностью (рис. 3).

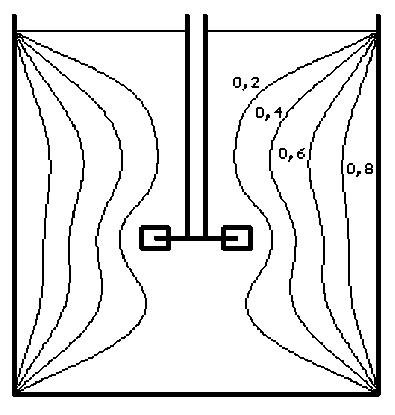
Рис. 3. Картина изотерм в аппарате при Re = 50, Pr = 0,05

Увеличение числа Рейнольдса сопровождается интенсификацией радиально-тангенциальных потоков. Роль конвекции в переносе теплоты возрастает. Особенно заметна тенденция к усилению конвективного переноса теплоты в области мешалки. Нагретые массы жидкости увлекаются быстро движущимися потоками, способствуя перемешиванию и постепенному выравниванию температур (рис. 4).

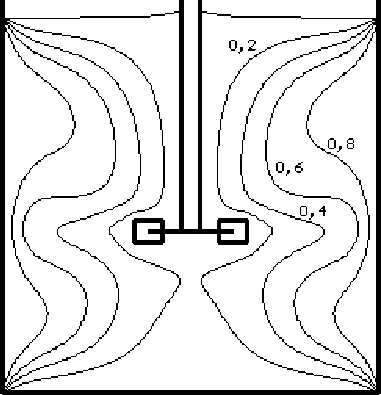
Рис. 4. Картина изотерм в аппарате при Re = 200, Pr = 0,05