Теплообмен при турбулентном течении несжимаемой жидкости в плоском канале с постоянной температурой стенок

Задача о теплообмене при турбулентном течении в плоском канале относится к числу классических задач гидродинамики. Ввиду отсутствия общепринятой теории турбулентности при аналитическом решении задачи прежде всего необходимо выбрать модели турбулентного течения и теплообмена. В данной работе используется модель пристеночной анизотропной турбулентности [1], [2]. В основу модели положены экспериментальные факты [13], [15], согласно которым в турбулентном потоке вблизи твердой стенки присутствуют когерентные вихревые структуры, существенным образом влияющие на характер течения. Вихревая структура образована плотной системой вихрей, вытянутых вдоль по потоку и наклоненных к нему. Их называют Л-вихрями, или подковообразными вихрями. Каждый вихрь имеет две ветви - восходящую и нисходящую. При удалении от стенки углы наклона вихрей растут, достигая 40-45° в точке, в которой восходящая ветвь переходит в нисходящую. Система вихрей создает локальную анизотропию потока, характеризуемую вектором, который называют директором. За пределами этого так называемого пристеночного слоя [1] вихревой характер течения сохраняется, но когерентность вихревой структуры отсутствует и поток является локально изотропным.

Принимая во внимание изложенные факты, при решении задачи плоский канал рассматривается как две бесконечные параллельные плоскости, область течения между которыми состоит из пристеночных слоев, прилегающих к плоскостям, и ядра течения. Для описания течения и теплопередачи в этих подобластях по необходимости используются разные модели.

ПРОФИЛИ СКОРОСТЕЙ

Полагая, что характер течения жидкости не зависит от температуры, прежде всего найдем распределение скоростей в потоке. Поскольку © Бабкин В. А., 2011

подробное решение задачи о профиле скоростей в канале можно найти в [1], [2], здесь приведено его краткое изложение.

Пусть ширина канала с горизонтальными плоскими стенками равна 2 H (рис. 1). Возьмем декартову систему координат x, y, z с осью x , лежащей в срединной плоскости канала и направленной по потоку, с осью y , направленной перпендикулярно плоскостям стенок, и с осью z , образующей с осями x и у правую систему. Таким образом, уравнения стенок у = ± H . В пристеночных слоях течение рассматривается в рамках модели анизотропной турбулентности [1], [2]. Описание движения среды и теплопередачи в ней производится только на уровне осредненных

величин, поэтому здесь и далее для параметров модели используются обычные обозначения без знака осреднения. Для несжимаемой жидкости общие уравнения модели (уравнения неразрыв-

ности, количества движения, динамики дирек тора и определяющие уравнения среды) в дека ртовых координатах х 1, х2, х3 имеют вид:

d P   д и _A

— + p—а = 0, dt    дx а du,     дp

P — i- = —— -■-dt

-

—

д xi

^{д (} a iа + ^Т iа )

^д X а

+ L

d [ dn ) 5Pta

— I I—- I = i + gi + Gi, dt ( dt J дx а

д п

а aij

v дПа j = K —- —j

д x, ⁱ

—

^{д x} а    ^{д X}j

д п

— + nn р

д п

а

)

дx р; ’

Т- = ал П_пе оП п + Цл^ ij    г*1 а р ар i jj ^0 j

%=к1п1 + к fin-^дxj

gi = X п

—

—

д n j ^дXi

—

nn а

^{д X} а )

' ^{: к п |} + кп ^{д x} р

д п р д п р

а

дX а дxi

e u =

1 ( ди, ди. ) --i - + —^

2 Эх, 8х

При условии, что стенки канала гладкие, граничные условия задаются равенствами [1], [2]: sin 0 ( ± Н ) = 0,     и ( ± Н ) = 0 .       (11)

где р - плотность жидкости, и. - локальная скорость, п- директор, p - давление, а.. - напряжения, обусловленные наличием в среде вихревой структуры, т .. - вязкие напряжения, в . - обобщенные напряжения, e j - скорости деформаций, f, G . - массовая и обобщенная массовая силы соответственно, g - обобщенная внутренняя массовая сила, I, K , ц₀, ц 1 - определяющие коэффициенты модели, к . , х - произвольные векторная и скалярная функции. Здесь и далее по одинаковым индексам предполагается суммирование от 1 до 3.

Интегрирование уравнений (9), (10) с граничными условиями (11) дает необходимые далее зависимости 0( у ), и ( у ) в виде [1], [2]

cos 0 = [1 - 3 bH (1 -|^| )]^1/3, ^ = y / Н , (12)

и = Аи . [ ф®-Ф (1) ] , Ф® = F ( t О,

t ($ = [1 - 3 ЬН (1 -^| )]^1/3,               (13)

F(t) =

2 y ² - 1

^ arctg ^

Л

+ 1 ln t + 2 1 + 1

1 J

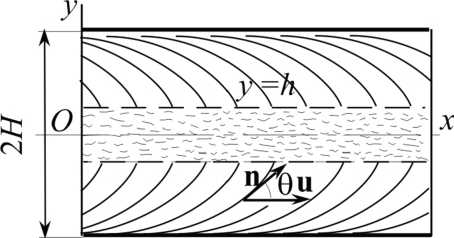
Рис. 1. Схема течения

1 + 2 8 ₇ Y ² - 1 ² ln

4 ( 2 y ² - 1 ) t ² +y ² - 1

+ ¹ In I t ⁴

-

t ² -8

t ²

A = -2^ . , £ = -^ 0-, и. =      , 2 Y ² = 1 + V 1 + 4 8 ,

3 ц b ² R    2 ц      p p ^Г

Вернемся к рассматриваемому течению в канале в координатах x, y, z. Пусть вязкая несжимаемая жидкость в канале находится в режиме установившегося турбулентного течения. Длина канала бесконечная, стенки гладкие. Найдем вначале профили скоростей в пристеночных слоях. Воспользуемся уравнениями (1)-(7). Коэффициенты ц0, ц1, I, K приняты постоянными. Если пренебречь массовыми силами f. и G., то течения в пристеночных слоях можно считать симметричными относительно срединной плоскости у = 0. Область течения |у| < H будем рассматривать как объединение трех подобластей: два пристеночных слоя h < |у| < H и ядро течения |у| < h, где h - полуширина ядра течения. Скорость и., директор п. и давление р в пристеночных слоях отыскиваются в виде их = и(y), uy = uz = 0, nx = cos 0(y),

П у = sin 0 ( y ), n = 0, p = p ⁽ x ) + p ₂ ⁽ y), (8) где 0 - угол между директором п. и осью x .

Подстановка выражений (8) в уравнения (1)(7) после несложных преобразований приводит к уравнениям для и ( у ) и 0( у ):

( ц ,sin² 0 cos² 0 + —) и' = -т —, т = - — Н (9)

1               2 ^w Н ^w      д x ’

0‘‘ sin 0 cos 0 + 0‘ ²(1 - 3sin² 0 ) = 0,         (10)

где (d pIdx )- постоянный вдоль потока градиент давления, T_w - модуль касательных напряжений на стенках канала, штрихами обозначены производные по у.

где b - постоянная интегрирования.

Профиль скоростей (13) справедлив только в прилегающих к твердой стенке пристеночных слоях. Толщину слоев можно найти на основе анализа опытных данных. По данным [13], [15], в развитом турбулентном течении при наибольшем удалении вихревых линий от стенки их угол наклона к направлению течения близок к 45°. Будем считать, что границы пристеночных слоев у = ± h определяются условием того, что на границе слоя 0 = 45°. Тогда из формулы (12) сле-

дует

h _4-V2 Н = 12 ЬН '

Толщина пристеночного слоя А = H - h , очевидно, определяет размер ядра течения. Если вер-

шины пристеночных вихревых линий в среднем достигают срединной плоскости, то ядро течения исчезает, то есть h = 0. В этом случае полуширину канала назовем H max . Из (14) следует

^Нтах    12 b

Таким образом, если полуширина канала H < H , то использование рассматриваемой мо-max дели справедливо по всему сечению канала. Например, при сопоставлении с опытными данными для течений воздуха найдено, что в трубах и каналах b ~ 4,83 м-1 [3] и, следовательно, в них Hmax - 45 мм.

Если H >  H m_ax , то в ядре течения для отыскания поля скоростей необходимо использовать другую модель. При выборе модели воспользуемся свойствами турбулентной вязкости. Анализ экспериментальных результатов показал, что в ядре течения турбулентная вязкость изменяется слабо и приближенно ее можно считать посто-

янной [6], [10], [11], [16]. Кроме того, согласно [14], [17], максимальное значение турбулентной вязкости достигается вблизи границы пристеночного слоя и ядра течения.

Как следует из формулы (9), здесь турбулентная вязкость задается формулой цт = (ц0 /2) + ц1sin29cos2 9. (16)

На границе пристеночного слоя и ядра течения (9 = 45°) турбулентная вязкость (16), очевидно, принимает максимальное значение

Из сравнения с опытными данными при течении воздуха в трубах и каналах при нормальных условиях (температура 20 °С, давление 760 мм рт. ст.) для модельных констант были получены равенства [3]:

b = 4,83 м-1, ц0 = 1,85 • 10-6 Па • с, ц1 = 0,047 и * Па • с.                 (18)

Расчеты [4] показали, что при коэффициентах (18) вязкость рто имеет значения, весьма близкие к экспериментальным [14], [17], поэтому с учетом сказанного выше в ядре течения турбулентную вязкость примем постоянной и равной рто. Тогда уравнение (9) в ядре принимает вид duy

Ц T0-;7 = -т w tH, 5 =—■(19)

d5

Интегрируя уравнение (19) при условии не- прерывности скорости на границе пристеночно го слоя и ядра § = ^0, получим, что при |y| < h u = uo + ^H(52-52), ^.1 = h-, u * u * 2ц to

где расстояние §₀ и скорость u_Q — величины, вытекающие из формул (13) и (14):

1 5 «1 = 1 -4—7, и 0 = Au - [ ^ф(5 о )-^ф(1> ] . (21)

12 bH

Таким образом, формулами (13) и (20) профиль скоростей определен во всей области течения. На рис. 2 для примера приведены расчетные профили скоростей (13), (20) при течении воздуха в канале шириной 2 H при числах Рейнольдса Re = 480 000 и 920 000. Числа Рейнольдса определены формулой

4 wH

Re =---- v

где w - средняя скорость потока, v - молекулярная кинематическая вязкость. Для сравнения точками представлены результаты экспериментов Конт-Белло [5] при этих же числах Рейнольдса. Расчетные профили скоростей (сплошные кривые) вычислены в условиях эксперимента и при значениях для b, ц0 и ц1, заданных формулами (18). Согласие результатов достаточно удовлетворительное. Небольшое расхождение расчетных и опытных данных у срединной плоскости потока вполне объяснимо приближенным характером предположения цт0 = const по всему ядру течения.

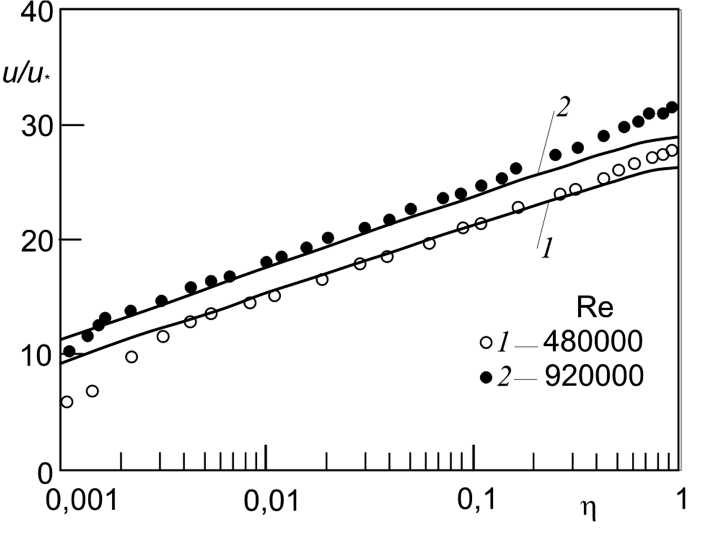
Рис. 2. Сравнение расчетных профилей с опытными данными: кривые — расчет по формулам (13), (20), точки — опытные данные [5]

ТЕПЛООБМЕН

При решении задачи о теплообмене уравнения (1)—(3) необходимо дополнить уравнением притока тепла, которое в декартовых координатах х имеет вид [1], [4]

р dU = (_ p5+ aij + т^ + рN — gN + Q *q, (23) dt dxt где U - внутренняя энергия единицы массы, Q -интенсивность источника тепла, q. - поток тепла, а.., т., вj — напряжения, g. — обобщенная сила, соответственно определенные формулами (4)— (7). Кинематические параметры N., N.. определяются формулами дн      дп

N, = n, - ю,„ n„, N,=-n- - Ча ■ , (24) 5xj      5xj dn,           1 fа и, а и ^

n i =        , to ij =                       I .

dt            2 ^c x. d x . J

Конкретно задача о теплообмене в плоском канале формулируется следующим образом. Пусть в плоском канале, ограниченном гладкими параллельными стенками, в режиме установившегося турбулентного течения движется несжимаемая жидкость. Система координат и схема течения даны на рис. 1. Пусть во входном сечении х = 0 температура Т постоянна. Найдем распределение температуры Т в полубесконечной по оси х области х > 0 при условии, что температура T w на стенках одинаковая и постоянная. Как и при определении профиля скоростей, задача о распределении температуры в пристеночном слое и ядре течения рассматривается отдельно.

С учетом симметрии явления в принятой выше системе координат x , у, z температуру T будем отыскивать в виде T = T ( x , у). Вследствие известной глубокой связи между процессами переноса импульса и тепла при турбулентном течении теплопроводность турбулентной жидкости в пристеночном слое, как и выше турбулентную вязкость, будем считать зависящей от локальной анизотропии потока, то есть от директора n. (i = x , у , z ). Поскольку T = T (x, у), закон Фурье принимает вид [1], [4]

1 2\8 T -1       8 T qx = -(X0 + X1 nx )    - X1 nxny ^-,

^{8 x          8 у} (25)

7       8T ..     . 2. 8T qy = -X1 nxny — - (X о + X1 ny)—, 8x            8у где Xo и X1 - определяющие коэффициенты модели, характеризующие турбулентную теплопроводность среды.

Как видно из (25), если пренебречь теплопроводностью в направлении течения, то коэффициент турбулентной теплопроводности ^ в пристеночном слое определяется формулой

X T = X ₀ + X 1 n 2 =X ₀ + X 1 sin² 9 .        (26)

Уравнение распространения тепла в потоке, необходимое для решения поставленной задачи теплообмена, следует из уравнения притока тепла (23) после некоторых преобразований. Подставим в уравнение (23) равенства (24), (25), заменяя попутно координаты скорости и и директора n i их выражениями (8); выразим внутреннюю энергию U через энтальпию i = c T и проведем обычно принятую в подобных задачах оценку вклада различных членов уравнения в перенос тепла [9], [10]. Тогда, считая используемые коэффициенты Х_о и Х 1 постоянными и пренебрегая производством тепла ( Q = 0), получим искомое уравнение распространения тепла в пристеночном слое в виде

8 ² T           8 T          8 T

^(х о ^{+ X} 1^{Sin 9} )      + ^X 1 ⁹ sin ^{2 9} — = р C p U ⁽ у )—, (27)

8 y 2            8y           8 x где c - теплоемкость при постоянном давлении, и (у) - профиль скоростей (13), штрихом обозначена производная по у.

В ядре течения коэффициент турбулентной теплопроводности X T _o, как и турбулентную вязкость, будем считать постоянным и равным турбулентной теплопроводности X на границе областей | у | = h :

2X T0 = 2X 0 +X1.(28)

Тогда уравнение распространения тепла в ядре течения имеет вид

XT0 |^T = РCpU(У)8T ,(29)

8у где и (у) - профиль скоростей (20).

При решении задачи удобно перейти к безразмерным величинам

0 =

T - T

w

Т -Т ’

T ₀ T _w

X = -,   9 =

HH

Уравнения (27) и (29) можно рассматривать как одно уравнение во всей области течения, которое после подстановки в него соответственно профилей скоростей (13) и (20) в безразмерных переменных (30) имеет вид

520     50      50

⁸⁰ + Т₁ ( 9 )Ч' ( 9 )⁸⁰

[0,

⁰ 1 ( 9 ) =

* -        2 X 1 bH

. 1 ( 9 ) [ x 0 +X 1 (1 - 1 ² ( 9 ))]’

Р C p U ( 9 ) H

. Ф Ф

X 0 +X 1 (1 - 1 2 ( 9 ))

I 90I <9< 1,

0 <№ .

I 90I <9< 1.

Уравнение (31) должно удовлетворять граничным условиям

0(9,0) = 1, 0(±1,X) = 0, 80(0,X) = 0(32)

и условиям сращивания решений на границе областей 9 = 90

0(90" 0 ,x) = 0(90 ± 0 ,x ),

80 ( 9 0 "  0 ,X ) _ 80 ( 9 0 ± 0 ,X )

89      =      89'

Функции t (9), Ф(9) и величины и * , A в уравнении (31) определены формулами (13).

Принимая во внимание симметрию процесса теплообмена относительно срединной плоскости 9 = 0, ограничимся решением в области 0 < 9 < 1. Поскольку точное аналитическое решение найти не удается, будем отыскивать его приближенно методом Галёркина в виде

n

0 ( X , 9 ) = 2 g k ( X ) Ф к ( 9 ).              (34)

к = 1

Базисные функции ф k (9 ), удовлетворяющие в области 0 < 9 < 1 второму и третьему граничным условиям (32) и первому условию непрерывности (33), определим формулами

Ф к ^{( 9 )} =^Ф 0^{( 9 )cos(} k ^- 1) П⁹ ,             ⁽³⁵⁾

[ F 0 ( 1 ( 9 )) - F 0 (1),                    9 0 ^9^ 1,

^Ф 0 ^{( 9 )} Нф 0 ( 9 0 )

U ( 9 0 )

и ( 9 0 ) + ^р и ^{2 Н} ( 9 2 -9 ²) , 2 ц T 0

0 <9^9 0

F _o ( 1 ) = 2(3 bH - 1)ln^— ¹ ln ,^{Y 1} + ln 1 ⁴ - 1 ² - si + 2 1

⁰                       Y + 1 1 ² +y ² -1     ^{1            1}

где и (9₀) - скорость на границе пристеночного слоя и я⁰ дра течения.

Функции g k ( Х ) определяются стандартной процедурой метода Галёркина [7] с учетом первого граничного условия (32).

При известных функциях g k (Х ) формула (34) дает приближенное решение задачи. Местное число Нуссельта Nu = 4а H /X на одной стенке канала можно вычислить затем по формулам [9]

Nu( X ) =

4 X 0 fd®) хЦаЦ^

® ( X ) = - f©& X ) u( ^ ) d ^ w ₀

где а - коэффициент теплоотдачи, X - коэффициент молекулярной теплопроводности жидкости, ® - средняя массовая температура по сечению, w - средняя скорость в канале

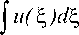
Для сравнения с опытными данными решение (34) было реализовано при следующих конкретных условиях. Жидкость - воздух при нормальных условиях: р = 1,205 кг/м³, v = 1,5 • 10^-5 м²/с, X = 2,57 • 10^-2 Вт/(м • К), c = 1002 Дж /(кг • К), число Прандтля Pr = 0,705. Коэффициенты ц₀, ц 1 и константа b заданы формулами (18). Коэффициенты X 0 и X 1 , входящие в формулу (26) для турбулентной теплопроводности, определены формулами

Х_о= 0,28 uH , X= 46 ,и .          (37)

0                  *             1                  *

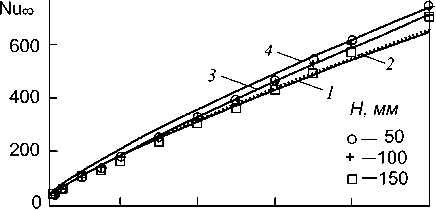
В результате расчета получены значения предельного числа Нуссельта Re = 5 • 10⁵ при течениях с числами Рейнольдса вплоть до Re = 5 • 10⁵ в каналах шириной 2 H = 100; 200; 300 мм (точки на рис. 3). Для сравнения на рис. 3 приведены также графики известных эмпирических формул.

800 --------------------------------------

1      10      20       30      40 Re-104

Рис. 3. Зависимость предельного числа Нуссельта Nw от числа Рейнольдса Re для каналов ширины 2Н. Точки - результат расчета, кривые - графики эмпирических формул: 1 - [9], 2 - [8], 3 - [10], 4 - [12]

Кривая 1 [9] :

Nu „

f Re Pr/ 8

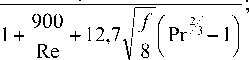
кривая 2 [8]:

Nu „= 0.021Re0.8 Pr0.43;(39)

кривая 3 [10]:

Nu„ = 7,6 —3,6- + 0,0096Re0'87Pr0'605 ;(40)

"   ’ IgRe кривая 4 [12]:

Nu =________________P (41)

” 4,24ln(Re V f /16) + 25,0 Pr^2/3 + 4,24 In Pr - 20,2 ’ где Pr - число Прандтля, Re - число Рейнольдса, f - коэффициент сопротивления, определяемые формулами

P^v c p       4 wH   .          1

Pr =--- ~, Re =       , f =----------------г.

X            v ’ J (1,821g Re -1,64)2

Как видим, рис. 3 демонстрирует достаточно удовлетворительное согласие расчетных и экспериментальных результатов вплоть до Re = = 500 000. Некоторое расхождение результатов вполне объяснимо хотя бы тем, что сами эмпирические формулы не совпадают между собой.

Представляет интерес сравнение процесса теплообмена в плоской трубе с теплообменом в круглой трубе [1], [4]. Обычно эти процессы рассматриваются как аналогичные [9]. Проявлением аналогии является прежде всего общий вид фор -мул (38)-(41) для обоих процессов теплообмена при соответствующем выборе параметров, через которые определяются безразмерные величины f, Re, Pr, Nu. Если сравнить решения задач о теплообмене здесь и в [1], [4], то нетрудно убедиться, что аналогия проявляется на каждом шаге. В частности, в обоих случаях величины ц₀, ц 1 и b одинаково определены формулами (18), а уравнениям (37) при течении в канале соответствуют аналогичные уравнения

Х_о = 0,28 uR , X, = 46,5 u* 0                  *             1                 *

при течении в трубе, где R - радиус трубы.

ЗАКЛЮЧЕНИЕ

Одна из основных трудностей при аналитическом или численном решении задачи, связанной с турбулентным течением жидкости, состоит в том, что в настоящее время неизвестна универсальная модель турбулентности. В связи с этим в последние десятилетия потребности практики стимулировали разработку довольно значительного числа моделей разной степени общности. В их число входит и использованная выше феноменологическая модель анизотропной пристеночной турбулентности. Она относится только к течениям, имеющим границей твердую стенку. Рассмотренная задача еще раз показала, что, как и при решении ряда задач ранее [1], [2], [3], [4], эта модель достаточно адекватно описывает класс пристеночных течений, позволяя аналитически определять как сопротивление, так и параметры теплопередачи.