Теплоотдача и сопротивление высокопористого материала

Пористые материалы хорошо зарекомендовали себя в системах охлаждения теплонапряженных узлов ракетных и газотурбинных двигателей, лазеров, атомных реакторов [1-3]. В системах, где существуют жесткие ограничения на гидравлические потери теплоносителей, как например в рекуперативных теплообменниках, более целесообразным является применение высокопористых ячеистых материалов (ВПЯМ), технология изготовления которых разработана в Научном центре порошкового материаловедения ПНИПУ (г. Пермь) [4, 5].

Теоретической базой применения ВПЯМ в теплообменных аппаратах служат:

• -    математическая модель геометрической структуры ВПЯМ (геометрическая модель);

• -    математические выражения для эффективных теплофизических свойств каркаса и теплоносителя в пористом материале (теплофизическая модель);

• -    математическое описание температурных полей в каркасе и потоке теплоносителя (модель тепловых процессов);

• -    данные о теплогидродинамических характеристиках пористого материала.

Геометрическая и теплофизическая модели ВПЯМ предложены в работе [6]. Модель тепло- Кирсанов Юрий Анатольевич, доктор технических наук, доцент, ведущий научный сотрудник.

вых процессов в пористом цилиндре, охлаждаемом однофазным теплоносителем при неизменной по длине цилиндра температуре образующей поверхности рассмотрена в работе [7], а при изменяющейся в продольном направлении температуре образующей поверхности – в работе [8]. Методика исследования теплогидродинамических характеристик пористых материалов описана в работе [7].

Тщательный анализ геометрической модели структуры ВПЯМ [6] выявил неточность в принятых допущениях, негативно отразившуюся на теплофизической модели и определении температурных полей в каркасе и потоке теплоносителя. Целью данной работы является устранение указанной неточности и экспериментальное получение теплогидродинамических характеристик ВПЯМ.

ГЕОМЕТРИЧЕСКАЯ МОДЕЛЬ ВПЯМ

Основным структурным элементом ВПЯМ является ячейка, представляющая собой по форме вытянутый эллипсоид вращения. Укладка ячеек близка к плотной упаковке шаров с 12 соседними ячейками, т.е. каждая пора в среднем имеет 12 отверстий (рис. 1, а ) [9].

Геометрическая модель ВПЯМ построена при следующих допущениях [6]:

• -    пористая структура однородна по всему объему;

• -    все поры сквозные, то есть глухих (непроходных) пор в пористом материале нет;

• -    пористая ячейка представляет собой комбинацию сферических пор диаметром d сф и соединительных каналов диаметром d к ;

• -    центры 4-х ближайших сферических пор

  

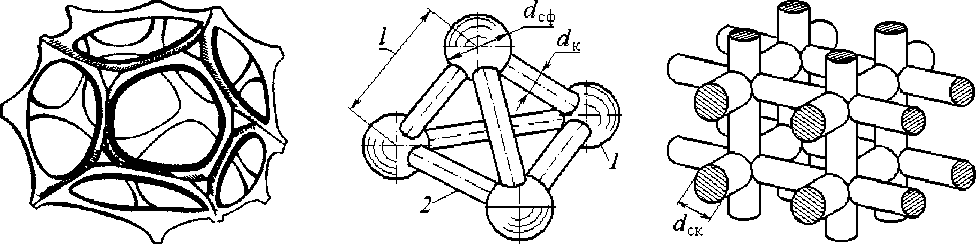
  Рис. 1. Структура ВПЯМ:

  а ) – ячейка ВПЯМ; б ) – внешний вид икосаэдра; б) – тетраэдрическая модель; 1 – сферическая пора; 2 – соединительный канал; в) – проволочная модель

  
  
  

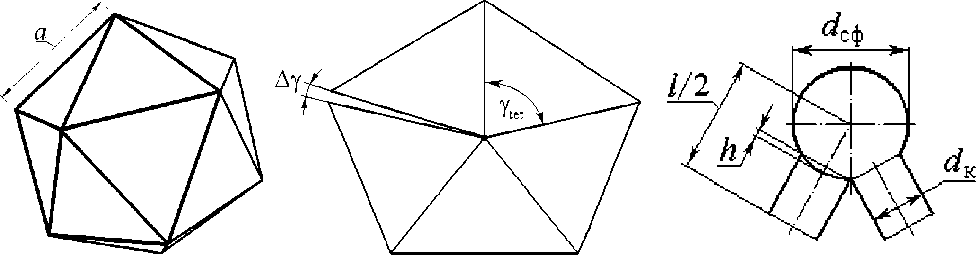
  Рис. 3. Многогранник из 5 тетраэдров

  
  

  Рис. 2. Икосаэдр

  
  

  Рис. 4. Геометрия пор

  
  

располагаются в вершинах тетраэдра на одинаковом расстоянии l друг от друга, а радиальные ребра тетраэдра являются осевыми линиями соединительных каналов (рис. 1, б );

• -    20 тетраэдров с общей центральной сферической порой образуют многогранник, имеющий 12 внешних вершин, каждая из которых является центром сферической поры.

Согласно этой модели, называемой тетраэдрической, центральная пора сообщается 12 каналами (отверстиями) с ближайшими 12-ю соседними порами, что соответствует реальной ячейке, показанной на рис. 1, а . Тетраэдрическая модель ВПЯМ позволила при заданных значениях диаметров сферы d сф и канала d к получить формулы для таких характеристик пористости, как объемная пористость Е v , эквивалентный гидравлический диаметр пористости d э , удельная поверхность f ск и эквивалентная толщина скелета З _ск (рис. 1, в ), удельная площадь поперечного сечения каркаса Е _ск и др.

Полученные в работе [6] формулы для характеристик пористости являются приближенными. Неточность заключается в том, что многогранник из 20-ти тетраэдров имеет объем, меньший, чем икосаэдр (рис. 2), у которого радиус описанной сферы совпадает с длиной ребра тетраэдра l . Причиной тому является то обстоятельство, что икосаэдр представляет собой комбинацию не из тетраэдров, а из многогранников, образованных из 20 пирамид, основанием каждой из которых является равносторонний треугольник со стороной a (рис. 2), а боковые или радиальные ребра, сходящиеся в центре икосаэдра, имеют длину [10] l - a -J2(5 + V5)/4 = 0,951 • a .

Угол между боковыми гранями пирамид в икосаэдре равен g = 2p/5 = 72°. У тетраэдра угол между боковыми гранями составляет Y tet - 69 о 5'41" , то есть Y _tet < Y , и поэтому при сложении 5 тетраэдров между гранями остается зазор Ay (рис. 3). Другими словами, в ранее рассмотренной тетраэдрической модели [6] занижен относительный объем каркаса в ВПЯМ.

Для уточнения формул, определяющих характеристики пористости ВПЯМ, рассматривается икоса-эдр¹, состоящий из 20 одинаковых пирамид, основанием каждого из которых является равносторонний треугольник со стороной a , а боковые или радиальные ребра имеют длину l . Вершины пирамид находятся в центре центральной сферической поры.

В икосаэдре выделяется контрольный элемент в виде третьей части пирамиды с одним радиальным ребром длиной l 2 . Контрольный элемент включает в себя 1/60 часть центральной поры за вычетом сектора y - 2 л/ 5 сферического сегмента² высотой h - ( d _с ф - ^ d _с ²ф - d , )j 2

(рис. 4), опирающегося на канал диаметром d к , и такого же сектора соединительного канала диаметром d к и длиной ( l - d сф)/ 2 + h .

Объем икосаэдра с ребром основания a составляет [10]

V„ „ - 5 ⁽ 3 ⁺⁾ a ³ - ⁴0 ^ ^{3 +}     , l ³ - 2,536 - 1 ³

¹²         372 ( 5 + 75 ) 3²               .

Объем контрольного элемента составляет 1/60 часть объема икосаэдра с длиной радиального ребра l 2 :

из-да расхождений функций F 1 ( d _к, l ) и F 2 I d _к, l ) • Расхождения составляют, примерно, 32 % при E _v = 0,8 и 27 % при е _v = 0,966.

Удельная поверхность пористой структуры равна отношению площади поверхности пор, заключенных в контрольном элементе, к объему этого элемента:

„   ^S nop 3У2 л ( 5 + _х5 )                 F ( d к , l )

f ск ^- Г ^-^Г    Й3 F 2 ^{( d} к , ^{l )- 991} ' 3 ,⁽³⁾

^ к.эл ^{5 d} eф ( 3 + 75 )?                  d^l

у =_____ ^{3 +} 5 _____/³ = 5 284 • 10 ^-3 /³

^Г к.эл                     у 2 ^{1 5,284 10} l ,

36V2 (5 + V5 )

что, примерно, в 1,076 раз превышает объем контрольного элемента тетраэдрической модели, рассмотренной в [6].

Объем пор, заключенных в контрольном эле-

что, примерно, в 1,86 раз больше значения этой величины по тетраэдрической модели [6].

Путем замены скелета эквивалентным ему по объему V_ск - ^{( 1 — e} v ^{) V} к эл и площади поверхности S пор проволочным каркасом (рис. 1, в ) получается формула для эквивалентного диаметра скелета:

менте:

^V пор

1 d

60 6

+1 « к (d + h

5 4

«h ² С 3 , I^- ”3" I2 ^d<

« d 3,

= ^ ^Fd-^l , ^h 1

где

Fd к , l , h ) - 1 + 9 d $ — 1 + 2 h ) — 12 h 2 3 2 h ) = (1 - d рд/1 - d k — 9 l | + 9 l - 5 ; d к - ^dк!^d сф ; l - l/d сф ; h ^- hid сф .

Поверхность пор, заключенных в конт-

рольном элементе:

X . «dk пор 60 5

( l — d_e;u    ^

«dKI----сф + h I -кd^h к 2 сф

« d 2,

- —сф F ( d к , l )

60 ^{2 к ,}

где F 2 ( d к , l ) - 1 + 6 d к ( l — 1 + 2 h ) — 12 h . 3

Объемная пористость представляет собой отношение объема пор V пор к объему контрольного элемента V к.эл :

e v = V nop/ V™ = b F d к , l , h )/ 1 3 . (1)

где

b 1 ^-

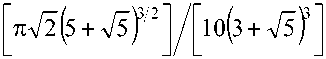
- 1,652

.

Эквивалентный гидравлический диаметр пористости d э определяется как отношение учетверенного объема пор к их поверхности:

d ₌ 4 V nop. ₌ 2 F i ⁽ d • - ¹ - h ⁾ d

’      S nop     3   F 2 ( d к , l )    сф •

Значения d э по формуле (2) меньше аналогичных значений по тетраэдрической модели [6]

³ В тетраэдрической модели [6] функция F ₂ ( d _к, l ) занижена из-за сокращения длины соединительного канала на высоту сферического сегмента h .

4У 20 (з+Vs) (1—ev)dj3        (1—ev)dcJ dc = V - 20 P+v5/ v -w«сф -0^4036 "w«сф .(4) ск Snop 3eV2 (5+x5);’ F2(dк, I)              F2(dк, I)

Относительная площадь поперечного сечения скелета еск есть отношение площади поперечного сечения проволочного каркаса (рис. 1,в), заключенного в кубе единичного объема, к площади одной из граней этого куба, то есть к 1 м2. Длина проволочного каркаса, заключенного в единичном кубе, составляет lпр - f:к / («dск ) , м/м •

На одно измерение (координату) приходится 1/3 часть этой длины и поэтому количество проволок единичной длины, приходящееся на одно измерение, равно

N пр ^{- l} пр /^{3 -} f ск /⁽³ « d ск ⁾ , 1/м².

Площадь поперечного сечения Nпр проволок равна относительной доле поперечного сечения каркаса е - fск «dс2к - fск dск ск   3«dCK 4       12 .

ск

После подстановки сюда формул (3) и (4) получается формула для е _ск при условии, что каркас не жесткий, то есть гибкий, так как он не содержит узлов, поскольку “проволоки” разных измерений не пересекаются друг с другом: е„ - 4 ( 1 — е , )/( 5 + 75 f² - ( 1 — e v )/ 4,866 . (5)

В случае каркаса с жесткой структурой, образованной пересекающимися друг с другом проволоками разных измерений, в местах пересечения проволок будут расположены узлы, количество которых равняется общему количеству проволок единичной длины. Суммарная длина, а отсюда – и количество проволок в единичном кубе N пр в этом случае возрастет по сравнению

с предыдущим случаем в з/( 3 — 2 d _ск j раза из-за того, что на образование одного узла придется длина, равная 1/3 диаметра скелета d ск одного измерения, а 2/3 длины узла покроются за счет длины проволок двух других измерений. В результате формула для относительной площади поперечного сечения жесткого скелета принима^ет вид к — / ''      ^1—- - ".-i-^{1 v}

• ( 5 + V5 У ^{3 —} с2 ^{d ск          3 2 d ск .}

Уточнение относительного объема каркаса икосаэдрической моделью ВПЯМ привело к тому, что при фиксированных величинах E v и d сф значения d э сократились, а диаметр перемычек d ск и удельная поверхность f ск увеличились; значения Е _ск благодаря росту d _ск несколько возросли при малых значениях E v и остались теми же при больших значениях E v .

МЕТОДИКА ОЦЕНКИ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК ВПЯМ

Формулы (1)-(6) включают в себя (помимо h , которая выражается через dк ) 7 величин: E v, I. d к - dэ - dск - fск и Еск - две из которых должны быть заданными, т.е. независимыми. На практике независимыми могут быть объемная пористость E v, диаметр пор dсф и межцентровое расстояние l .

При фиксированном значении l величина d к определяется из уравнения, получаемого из формулы (1):

• 6 x ³ — 9 lx ² + 9 1 — 5 — b 2 — 0 ,      ⁽⁷⁾

где x — V 1 — d к ; b ₂ — e _v l³ (b_x .

Уравнение (7) может иметь от одного до трех вещественных корней. Из них физический смысл имеет тот, который удовлетворяет условиям:

• 0 <  d к , d э <  1 ; f ск >  0 . _     (8)

Найденная таким образом величина dк вместе с известными значениями E v и i позволяет по формулам (2Н4), (6) вычислить dэ - dск - fск и Еск .

Выполнение условий (8), как и возможность определения остальных параметров пористости, во многом зависит от точности измерения независимых параметров. При правильной геометрической форме пористого образца (цилиндра, призмы) наиболее точно определяется величина E _v . При тщательных измерениях массы и размеров образца погрешность измерения E _v не превосходит долей процента. Величина d сф вычисляется как среднестатистическое значение измеренных диаметров пор на поверхности образца. При d сф ~ 10^-3 м погрешность измерения этой величины не превышает нескольких процентов. Наименьшей точностью измерения характеризуется величина l , так как положение центров пор приходится оценивать “на глазок”.

Для оценки диапазона возможных значений l по уравнению (7) были вычислены ее минимальные и максимальные значения (нижняя и верхняя границы) при разных значениях объемной пористости в диапазоне 0,78 <  E _v <  0,98. Вычисленные значения затем были аппроксимированы функциями:

l min — 1,9216 — 1,0946 -e _v + 0,3554 -e ^ ;

l max — 3,1721 — 2,5882 -e _v + 0,8705 -e ^ .

В табл. 1 представлены граничные значения наиболее важных для расчета теплового состояния геометрических характеристик ВПЯМ, рассчитанные при l ниж — 0,99 -lmin + 0,01 -1max

• ^и l верх — 0,01 - 1 min + 0,99 - 1 max ^.

Из табл. 1 видно, что границы изменения характеристик практически смыкаются при E _v = 0,80, а при E v ^ 1 разность между верхней и нижней границами в о зрастает. Наибольшая разность наблюдается у d э и f ск d сф , достигая, примерно, + 2,5% от середины диапазона при E _v = 0,98. Отклонение d _ск при E _v = 0,98 от его среднего значения составляет приблизительно

Таблица 1. Диапазоны изменения характеристик пористости ВПЯМ

E v	l ниж	l верх	d э при		f ск d сф при		d ск при		E ск при
			l ниж	l верх	l ниж	l верх	l ниж	l верх	l ниж	l верх
0,80	1,2772	1,6548	0,6172	0,6175	5,1846	5,1824	0,1543	0,1544	0,0458	0,0458
0,86	1,2465	1,5866	0,6222	0,6324	5,5289	5,4395	0,1013	0,1030	0,0309	0,0309
0,92	1,2184	1,5246	0,6275	0,6481	5,8645	5,6780	0,0546	0,0564	0,0171	0,0171
0,98	1,193	1,4688	0,6315	0,6648	6,2074	5,8964	0,0129	0,0136	0,0041	0,0041

+ 1,5%; на Е _ск величина 1 практически не оказывает влияния.

Сравнительно небольшие диапазоны изменений наиболее важных геометрических характеристик пористости ВПЯМ дают возможность использовать их значения, соответствующие средней ве л ичине относ и тельного межцентрового расстояния 1 _ср - ( 1 min + 1 max у 2 , аппроксимированные со средним квадратическим отклонением о :

dэ.ср - 0,3573+ 0,2923-ev, f.dсф)ср - 2,402+3,772-Ev, dск.ср -0,7481-0,7527-Ev, о- 2,3 -10-4;

о- 8 - 10 ^{- 3} ;

(9) о- 1,8 - 10 ^{- 3} .

Значения Е _ск рассчитываются по формуле (6).

ТЕПЛОФИЗИЧЕСКИЕ СВОЙСТВА ВПЯМ

Для расчета режимов теплопереноса в пористых структурах необходимы данные о геометрических и теплофизических свойствах этих структур. К теплофизическим свойствам относятся теплопроводность, плотность и теплоемкость пористой структуры и фильтрующегося сквозь нее теплоносителя.

Существуют различные подходы к оценке теплофизических свойств пористых материалов. В работах [11, 12] свойства каркаса (скелета) материала оцениваются совместно со средой, заполняющей поры. Такой подход оправдан тогда, когда заполняющая поры среда неподвижна и процесс переноса теплоты сводится только к теплопроводности материала, например, при оценке его теплоизолирующей способности. В случаях, когда через пористый материал течет теплоноситель, приходится учитывать его теплообмен с поверхностью пор в самом пористом материале, и тогда необходимы сведения о свойствах отдельных участников процесса переноса теплоты – каркаса и теплоносителя.

Плотность и объемная теплоемкость каркаса являются линейными функциями объемной пористости [11, 12]:

_ р _ск ^{- 1 -Е} v , ( р С ) _ск ^{- 1 -Е} v . ⁽¹⁰⁾ где р ск ^- р ск /р мат ; р ск ^- эффективная ^плотность каркаса, кг/м³; р _мат - теплопроводность материала каркаса, кг/м³; р c - объемная теплоемкость, Дж/(м³К); c – удельная теплоемкость, Дж/(кг·К).

По теплопроводности наибольшее число данных в литературе относится к низкопористым структурам. Так, относительную эффективную теплопроводность каркаса в случае щелевой и щеточной структур предлагается оценивать по формуле [3]

X ск - 1 - Е v ,

где X ск - X _ск /X _мат ; X _ск - эффективная теплопроводность каркаса, Вт/(м²К); X _мат - теплопроводность материала каркаса, Вт/(м²К).

Для канальной пористости рекомендуется соотношение [3, 13]

X ск - ( 1 -Е v )/( 1 + Е v ) .          (12)

Для спеченных зернистых, волокнистых и сетчатых материалов, трубчатых структур наряду с соотношением (12) применяют формулу [3, 12]

X ск - ( 1 -Е v )/( 1 + Е v ) 2 .        (13)

Для ВПЯМ В.Н. Анциферов и сотр. [13] предложили зависимость

X ск - ( 1 -Е v )/ 5 .

В работе [6], исходя из физических соображений, предложено относительную эффективную теплопроводность каркаса принять пропорциональной относительной площади поперечного сечения каркаса, то есть X _ск - Е _ск . Тогда согласно формулам (5) и (6) выражения для относительной эффективной теплопроводности каркаса ВПЯМ с гибкой и жесткой структурами:

Xск -(1 -еv)/4,866,(15)

• -            1 - Е„

X ск - 0,616----=^ .(16)

• 3 - 2 d ск

Зависимости эффективной теплопроводности каркаса от объемной пористости по выраже н иям (11)-(16) с подстановкой в формулу (16) d ск.ср из (9) показаны на рис. 5. Из рис. 5 видно, что в диапазоне Е _v >  0,8 значения относительной эффективной теплопроводности каркаса ВПЯМ, вычисленные по формулам (14), (15) и (16) практически совпадают друг с другом. Близ-

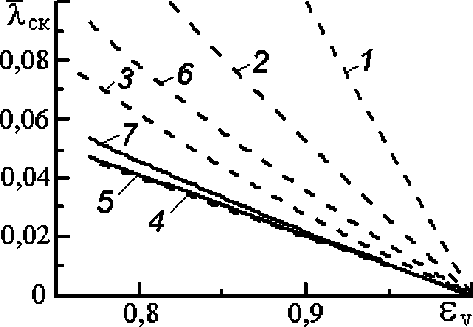
Рис. 5. Относительная эффективная теплопроводность каркаса по формулам: 1 – (11); 2 – (12); 3 – (13); 4 – (14); 5 – (15);

6 – тетраэдрическая модель [6]; 7 – (16)

ки к ним и значения X _ск , получаемые по формуле (13), чего нельзя сказать о значениях X _ск по формулам (11) и (12). Значения X _ск по тетраэдрической модели, рассмотренной в работе [6], при Е v - 0,8 превышают значения, получаемые по формуле (16), примерно на 80 %.

Относительные эффективные теплофизические свойства теплоносителя в пористом материале исходя из физических представлений логично определять по формулам:

^Р f,эф ^{- Е} v , ( ^Р c ⁾ f,эф ^{- Е} v ,

X фэф - 1 -Е _ск , (17) где ^p f,эф ^{- р} f,эф /^pf ; ^{( р} c ⁾ f,эф ^{- ( р} c ⁾ f,эф/^{( р} c f ; X f,эф - X f _э ф /X _f ; p _f , ( р с ) f и X f — свойства теплоносителя вне пористого материала.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ СОПРОТИВЛЕНИЯ ВПЯМ

Методика исследования гидродинамического сопротивления и внутренней теплоотдачи пористого цилиндра диаметром D ц и длиной l т описана в работе [7]. Геометрические характеристики исследованных 11 цилиндрических образцов ВПЯМ диаметром D ц и длиной l т рассчитаны по формулам (9) и (6) и представлены в табл. 2.

Коэффициент сопротивления пористых тел рассчитан по формуле

С

dэ

2 А p d _э

Р f W f² l т ’

где Аp - разность давлений теплоносителя до и после пористого тела, Па; wf - wf,o /(1 - Е ск ) -скорость фильтрации теплоносителя сквозь по- ристое тело, м/с; wf,0 – средняя скорость теплоносителя в канале без пористого тела, м/с; vf -кинематическая вязкость теплоносителя, м2/с; lт – длина пористого тела, м.

Результаты расчетов С d_э для исследованных образцов показаны на рис. 6, а .

Обобщение результатов обычно производят с помощью модифицированного уравнения Дарси dp

-"Г -а г 4 f w f + р г Р f w f , dz

или линейным уравнением регрессии

^ d э ^- A г + B г/^R e d э .           (20)

Здесь а г и р г - вязкостный и инерционный коэффициенты сопротивления пористого материала; ^ _f - р _f v _f - динамическая вязкость теплоносителя, Па^.с; A г и B г – коэффициенты регрессии; Re d э ^{- w} f ^d 3 /^v f – число Рейнольдса.

Между коэффициентами а г и р г , с одной стороны, и A г и B г , с другой, существует связь:

A г - 2 d э Р г , B г - 2 d _г ² а г . (21)

Путем аппроксимации точек, показанных на рис. 6, а , уравнением (20) для каждого образца были найдены коэффициенты A г и B г , а по формулам (21) затем рассчитаны коэффициенты а _г и Р г , значения которых даны в табл. 3. Аппроксимация полученных значений а _г и р г методом Гаусса, показанная на рис. 6, б и рис. 6, в , позволила получить следующие критериальные уравнения:

а г d с²ф - C „ Е V⁷⁵,⁶ ( 1 -Е v ) ^{- 5},⁰ d сф ( l ,/ d сф ) ⁵'⁶ . (22)

Р _г d сф - C р Е v³¹⁷ ( 1 - Е v ) " ⁰’⁹⁹ d С _: ( / ,/ d сф ) 6’⁹ ,(23) где C _а = 5,82^10 - ¹⁷, C р = 2,5440 - ¹³; d сф - диаметр

Таблица 2. Характеристики образцов ВПЯМ

Образец	Материал	D ц - 10 3 , м	l т - 10 3 , м	Е v	d сф • 10 3 , м	d э •Ю3 , м	d ск • 10 3 , м	Е ск	f ск , м -1
1	Медь	50,2	39,8	0,965	3,05	1,950	0,131	0,0119	1979
2	Нихром	49,9	33,7	0,954	3,49	2,220	0,200	0,0160	1719
3	Нихром	50,1	34,2	0,804	0,80	0,474	0,214	0,0794	6787
4	Нихром	49,9	34,2	0,871	3,93	2,402	0,659	0,0483	1451
5	Нихром	50,0	34,1	0,844	2,16	1,304	0,448	0,0603	2588
6	Медь	49,7	39,2	0,966	5,27	3,371	0,221	0,0117	1146
7	Нихром	50,0	41,3	0,867	1,98	1,206	0,34	0,0502	2876
8	Нихром	50,1	34,0	0,867	3,00	1,829	0,520	0,0500	1897
9	Медь	49,7	39,0	0,965	3,79	2,424	0,162	0,0119	1593
10	Медь	49,8	38,6	0,959	5,24	3,337	0,267	0,0143	1149
11	Нихром	49,6	33,7	0,800	0,80	0,473	0,220	0,0816	6764

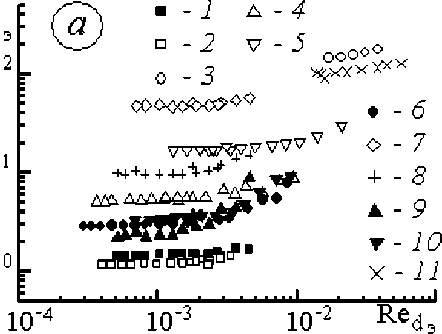
^d

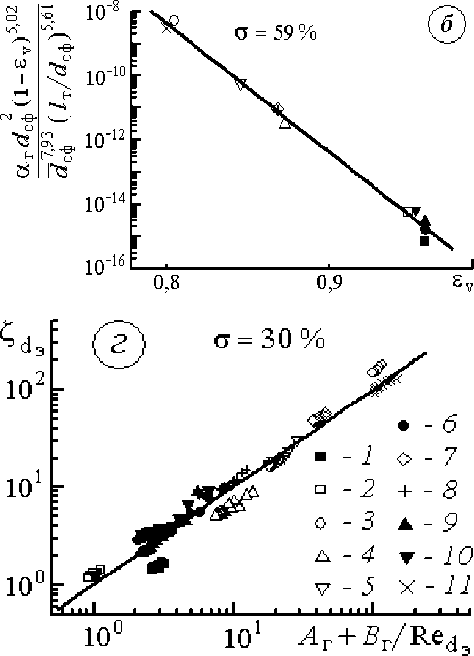
Рис. 6. Гидродинамическое сопротивление образцов ВПЯМ а – индивидуальные характеристики; б – обобщение вязкостного коэффициента сопротивления; в – то же инерционного коэффициента; г – обобщенная характеристика; 1-11 – номера образцов

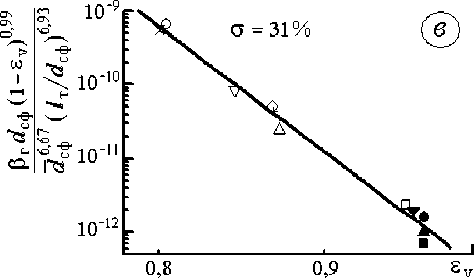
Таблица 3. Значения коэффициентов уравнений (19), (20) и (24)

Параметры Образцы 1 2 3 4 5 6 7 8 9 10 11 A г 1,442 1,097 103,5 4,075 13,030 2,562 37,02 7,304 1,687 2,353 76,68 B г 61,78 64,56 1054 256,2 398,6 520,5 354,5 288,3 384,0 730,6 517,2 ar -10"6, м-2 8,122 6,550 2346 22,19 117,1 22,90 121,8 43,05 32,69 32,80 1156 P г -10 , м-1 3,698 2,471 1092 8,481 49,95 3,801 153,5 19,95 3,481 3,525 810,7 (Pг /ar )-105, м 4,553 3,773 4,653 3,821 4,266 1,660 12,60 4,636 1,065 1,075 7,012 Aт -103 4,26 3,65 2,82 5,15 4,24 5,49 3,82 2,85 8,16 8,35 1,49 nт 1,11 1,11 0,88 1,15 1,01 1,10 0,99 1,15 1,06 1,10 0,98 сферической поры, отнесенный к 1 мм.

Опытные значения С d_э затем были обобщены уравнением (20), в котором коэффициенты A г и B г рассчитаны по формулам (21)-(23). Результаты обобщения показаны на рис. 6, г .

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

ВНУТРЕННЕЙ ТЕПЛООТДАЧИ ВПЯМ

Опытные значения внутренней теплоотдачи для отдельных образцов обобщались критериальным уравнением вида:

Nu l * - A _т Re П *^т Pr f^0,4 C _t , (24) где Nu i * - a l ,X f ; Nu i * -a _v ( l ) /X _f ; a -поверхностный коэффициент теплоотдачи, Вт/ (м²К); a _v - af ск - объемный коэффициент теплоотдачи, Вт/(м³К); l * – определяющий размер, м; с t - ( ^ f /^ w ) ^{0,14 -} для газов; c t - ( Pr f/ Pr w ) ^0,25 – для жидкостей.

Среди исследователей с * уществуют разные мнения по вопросу выбора l * . Так, В.М. Поляев и сотр. [1, 2], Ю.А. Зейгарник, Ф.П. Иванов [14]

и др. полагают, что в качестве такового следует брать отношение Р г /аг . Ю.Ф. Гортышов и сотр. за определяющий размер брали средний диаметр пор d сф [15] и диаметр трубы D [16]. Японские исследователи Fukuda K. и сотр. [17] предложили l = ij^ а _г и l * = 1[ р г . Авторы данной работы считают целесообразным по аналогии с обычными каналами использовать в качестве определяющего размера эквивалентный диаметр d э .

На рис. 7 показаны результаты исследования теплоотдачи 11 образцов ВПЯМ, обобщенные уравнением (24) при l * = р г /а _г (рис. 7, a ), при l = d сф (рис. 7, б ) и l = d ‘э (рис. 7, в ). Значения множителя A т и показателя степени n т при l = d ‘э даны в табл. 3.

Анализ графиков на рис. 7 показывает, что, во-первых, полученные результаты по внутренней теплоотдаче удовлетворительно согласуются с критериальным уравнением Ю.Ф. Гортышо-ва и сотр. [15]

Nu v,d сф - ^{0,606 Re} d сф Pr f ^£ V^5,2 (25)

и лежат ниже критериального уравнения В.М. Поляева [1, 14]

\u. 0,004 Re р_/а Pr_f , (26) полученному по результатам исследований низкопористых материалов.

Во-вторых, примерно одинаковые значения среднего квадратического отклонения о точек на рис. 7,a-в относительно критериального уравнения (24) свидетельствует, что ни один из определяющих размеров l не имеет заметных преимуществ перед остальными. Поэтому напрашивается вывод: для обобщение данных по внутренней теплоотдаче в пористых телах необходимо привлекать индивидуальные характеристики пористой структуры.

На рис. 7, г показано обобщение опытных данных по внутренней теплоотдаче ВПЯМ, полученных с использованием икосаэдрической модели ВПЯМ, критериальным уравнением \_ч - 2 32-ю ³ Re ¹;;’ d ¹¹ _; ,8 2 d сф/ d _С к ) ⁰,¹⁹ ( / -ск d J^X⁴ C t .(27)

Уравнение (27) построено методом Гаусса с выбором главного элемента в столбце. Среднеквадратическое отклонение точек от уравнения (27) составляет 23 %, что вдвое меньше отклонения точек от критериального уравнения (24).

Уравнения (20) и (27), обобщающие полученные результаты по гидродинамическому сопротивлению и внутренней теплоотдаче ВПЯМ, пригодны в диапазоне 14 <  Re d э < 3414.

ЗАКЛЮЧЕНИЕ

• 1.    Предложена икосаэдрическая модель ВПЯМ, позволяющая уточнить наиболее важ-

  

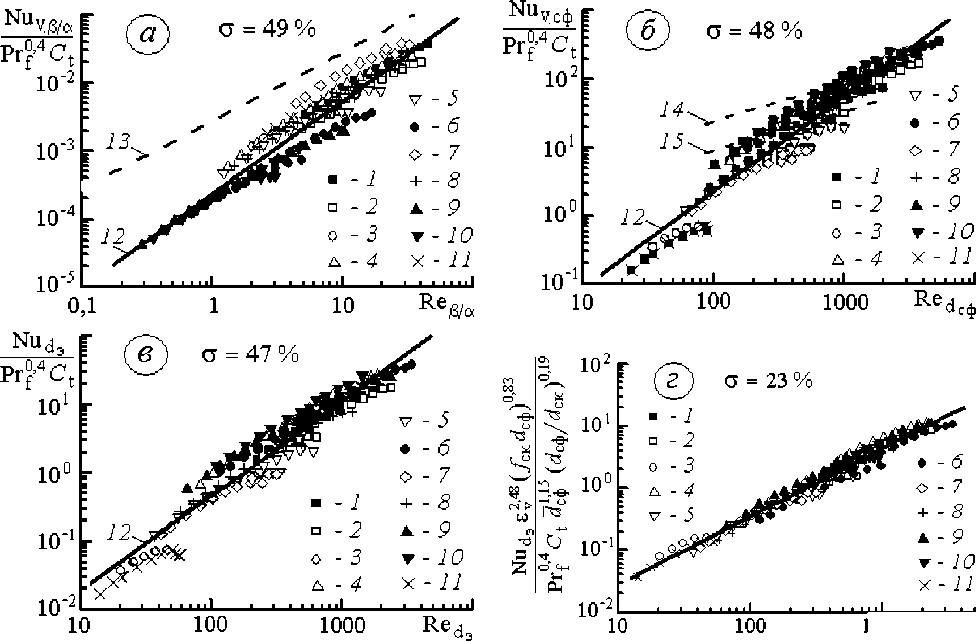
  Рис. 7. Теплоотдающие характеристики ВПЯМ:

  1-11 – номера образцов; 12 – 12 – линии регрессии опытных данных с использованием икосаэдрической модели ВПЯМ; 13 - уравнение (25); 14 - уравнение (26) при £ v = 0,8; 15 - то же при £ v = 0,97

  1000 Re_da

  
  

• 2.    При обобщении результатов исследований внутренней теплоотдачи и сопротивления необходимо помимо влияния режима течения, определяемого числом Рейнольдса, влияния теплофизических свойств теплоносителя, определяемого числом Прандтля, учитывать также влияние характеристик пористости пористой структуры.

• 3.    Полученные теплогидродинамические характеристики ВПЯМ применимы в диапазоне 14 <  Re_d < 3414; 0,8 < _Е < 0,966; 0,8 э v

ные для теплового и гидродинамического расчета геометрические и теплофизические характеристики ВПЯМ.

• < d сф <  5,27 мм.