Теплоотдача в каверне газовой турбины ЖРД

 in geostationary area]. Available at: (accessed 1 September 2013).

При проектировании энергетических установок летательных аппаратов необходимо учитывать большое число факторов, влияющих на надежность и энергоэффективность изделия. Одним из таких факторов являются тепловые потоки, образующиеся в результате теплоотдачи и трения газового потока при течении в газовых магистралях энергоустановок. Неучтенное в расчете тепло при проектировании узлов и агрегатов влияет на теплофизические свойства рабочего тела. Нерасчетные величины вязкости и плотности рабочего тела могут вывести рабочие параметры за предел расчетного объема работы установки, который для получения максимального КПД имеет довольно узкий диапазон величин [1]. Широкая классификация закрученных потоков встречается в энергетических установках летательных аппаратов, это обу- словлено интенсивностью протекающих динамических и тепловых процессов. Вращательные и закрученные потоки часто используются для интенсификации теплообмена в различных энергетических установках, в том числе в теплообменных аппаратах жидкостных ракетных двигателей (ЖРД) [2; 3]. Враща- тельное течение также характерно для подводящих и отводящих устройств газовых турбин и насосов ЖРД, полостей между ротором и статором турбин, торцевых щелей между вращающимся диском и корпусом, полостей гидродинамических уплотнений [4]. Актуальность исследования теплоотдачи в кавернах газовых турбин подтверждается многочисленными исследованиями в этом направлении [5-10].

Течение вблизи плоского диска радиусом r , равномерно вращающегося в покоящейся жидкости с постоянной угловой скоростью ю вокруг оси, перпендикулярной к плоскости диска, является одним из примеров точного решения уравнения Навье-Стокса [11].

При рассмотрении течения в полости вращения (каверне) необходимо разделять задачу на течение у вращающегося диска, и течение рабочего тела у неподвижного основания [6]. Для получения аналитиче- ского решения теплоотдачи при ламинарном течении потока рабочего тела у вращающегося диска, исполь- где ф и ф - продольная и поперечная координаты; Hф и Hф - коэффициенты Ламе; 5*ф - толщина потери энергии в поперечном направлении течения; 51ф - толщина потери энергии в продольном направлении течения. Толщина потери энергии потока в продольном направлении течения:

⁵ t

_ **       U T — Т о

5/ф =        1-- dy .             (2)

₀ U V    T 5 T O /

На рис. 1 представлено распределение относительного изменения профиля скорости и температуры в ламинарном пограничном слое для случая Pr < 1, что характерно для реальных рабочих тел газовой турбины. Толщина динамического пограничного слоя 5 утоплена в толщине температурного пограничного слоя 5 _t , T - температура в толщине пограничного слоя; Т _о ^ - температура обтекаемой поверхности, u - скорость в пограничном слое; U - скорость вне пограничного слоя.

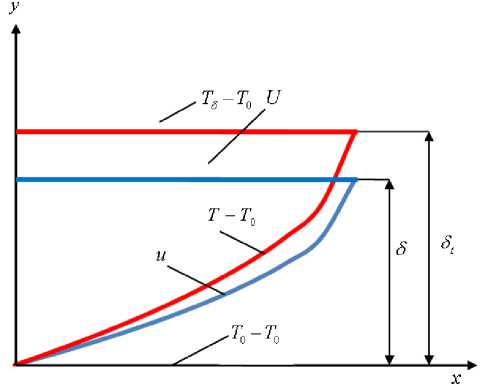
Рис. 1. Распределение профилей скорости и температуры в ламинарном пограничном слое при Pr < 1

зуется интегральное соотношение уравнения энергии

пространственного пограничного слоя, полученное путем интегрирования дифференциального уравнения энергии по толщине пограничного слоя в [12]. Без учета диссипативного члена в правой части соотно-

При определении толщины потери энергии в продольном направлении потока для случая описания безразмерного профиля скорости и температуры используется функция [6; 13]

шение примет вид 1 д „**     1 д

—т" 5 _{1 Ф} +--——

H _Ф ^дФ    H ф N

+--

.** ,      1     ^д H ф .*

t ^ф H Ф H ф дФ t ^Ф

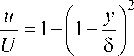
Т — Т о

Т 5 — Т о

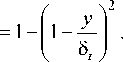
д H .

-5.

H ₉ H ф ^д ф

**

' t ф = St ,

С учетом отношения толщины температурного пограничного слоя к динамическому А = 5 / 5 _t = Pr^1/3 [14], а также функций (3) получено выражение для

определения толщины потери энергии в продольном

потока в поперечном направлении w и скоростью

направлении

** 5 ( 10 - 10 А + 5 А ² -A 3 )

^S ‘^ф =          30 А

При вычислении толщины потери энергии в продольном направлении (2) согласно принятой модели распределения профилей скорости и температуры, пределы интегрирования были разбиты на два участка: от 0 до толщины динамического пограничного слоя 5 и от 5 до толщины температурного пограничного слоя 5 t .

Закон теплообмена в виде критерия Стантона, входящий в левую часть интегрального соотношения (1), требует определения производной на поверхности теплообмена по функции температуры (3):

У t — T )1 - L _- 2А I T 5 - T o JJ y _{- 0} -5 ""5"

Выразив из (4) толщину динамического пограничного слоя 5 и проведя подстановку в (5), закон теплообмена можно записать в виде

St -

X р CpU

5 Г T - T o 3      X ( 10 — 10 А + 5 А ² - А ³ )

-' V ^{т т} JJ _y -0 =       15 5 , *ф р CpU

Для перехода к решению задачи конвективного теплообмена при реализации вращательных течений необходимо при рассмотрении интегрального соотношения уравнения энергии (1) перейти к цилиндрическим координатам. Учтем, что при вращательном осесимметричном течении (линия тока – кольцевая линия) : ф - a ; у - R . Коэффициенты Ламе для ци

линдрических координат Hф - Ha - R; Hу - HR -1 [15], тогда производная для коэффициентов Ламе определяется как аHф_аHа_аR   . аH*_ а

----- - ----- - --- - 1 ; ----- - --- - 0 .    (7) ду   а R   а R      дф da

С учетом (7) и закона теплообмена в виде критерия Стантона (6) интегральное соотношение (1) урав-

нения энергии запишется в виде

,_;     5 xM.-.V 5 А А )

а ^{Rt у + R}        15 5 *ф р CpU

Для получения аналитического решения соотношения (8) необходимо установить связь между толщиной потери энергии в продольном направлении 5 ** и входящей в левую часть соотношения толщиной потери энергии в поперечном направлении 5 ** . Тол-

щина потери энергии в поперечном направлении

в общем виде описывается выражением

⁵ 1                      \

5,„ - (- 1--- \Уу .         (9)

t ^у

0 U V ^T 5 ^т 0 J

где w – скорость потока в поперечном направлении. Профиль скорости, дающий связь между скоростью

потока в продольном направлении U , установил

Г. Ю. Степанов [16]

U

u

— - U s—

Г

1 -

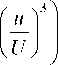
где s - тангенс угла скоса донных линий тока. Выражение (9) для толщины потери энергии в поперечном направлении потока с учетом (10) примет вид

5 *У - J

u

и , Г и s— 1 -I —

U

U

,3 )Г

I 1 -

т - T

T 5

-

T 0

dy .    (11)

Вычисление (11) производится аналогично (2). После несложных вычислений и преобразований получено выражение для определения толщины потери энергии в поперечном направлении потока:

** I ⁵ ,

5‘y-sl 3

233 5 491 5 ² 213 5 3

315 630 5 _t 770 5 3

.

Связь между толщиной потери энергии в поперечном направлении 5 ** (12) и толщиной потери энергии в продольном направлении 5 *ф (4) устанавливается путем введения относительной характерной толщины температурного пространственного пограничного слоя I , аналогичное отношение использовано в [16], с учетом А - 5 / 5 ₁ - Pr^1/3 имеем:

** т ₌ 1 ⁵ 1 у " s 5 , ф

( 8,3 А ³ - 23,38 А 2 + 22,19 А- 10 )

( А ³ - 5 А ² + 10 А- 10 )

.

Относительная характерная толщина зависит только от выбранных функций аппроксимирования относительного изменения скорости и температуры в пограничном слое и отношения толщины динамического и температурного пограничных слоев. С учетом относительной характерной толщины (13) интегральное соотношение (7) для течения с ламинарным пограничным слоем можно записать в другом виде:

_т а _s** i s _s** _^X ( ¹⁰ - ^{10 А} + ^{5 А} 2 ^s а r t ^{ф +} r t ^ф

-А3)

15 5 * ф р CpU

.

Рассмотрим случай вращательного течения газового потока в торцевой щели между ротором и статором лопаточной машины. Известно, что распределение окружной составляющей скорости потока по закону твердого тела характерно для диска, вращающегося в ограниченном пространстве. Аналогичный режим реализуется между вращающимся диском лопаточной машины и неподвижной стенкой корпуса. Согласно закону вращения твердого тела окружная составляющая скорости внешнего потока

U = r R .

С учетом (15) интегральное соотношение уравнения энергии пространственного пограничного слоя (14) примет вид

**

а 5 ** + ⁵ , ф -а r t ^ф r

X ( 10 - 10 А + 5 А ² -А ³ ) 1

15 1 sp Cp r

5 t ф R

- 0. (16)

Уравнение (16) решается как линейное дифференциальное уравнение первого порядка, в результате решения получено выражение для определения тол- щины потери энергии в продольном направлении по-

** тока δ _{t ϕ} :

**

^δ t ϕ ⁼

λ ( 10 - 10 Δ+ 5 Δ ² -Δ ³ )

15 I ερ Cp ω

С учетом (17) локальный закон теплообмена (6) можно записать в виде пригодном для численного интегрирования по радиусу торцевой щели:

λε ( 23,38Pr^0,66

St = 0, 258

- 8,3Pr - 22,19Pr^0,33 +

Cp ρω R ²

Следует отметить, что характер течения у неподвижной стенки (статора) может существенно отличаться от характера течения у вращающегося диска (ротора) [5]. В работе [6] получены выражения для определения величин ε – тангенса угла скоса донных линий для случая вращательного течения по закону «твердого тела» над неподвижным основанием (статором), и для случая вращающегося диска (ротора) в потоке, закрученном по закону твердого тела. При преобразовании (18) к критериальному виду учтем, ρωR2 ωR2        µCp что Re == и Pr =    ; Nu = StRePr ,

ωµν    λ а также известные значения ε – тангенса угла скоса донных линий тока [6]. Локальный коэффициент теплоотдачи в неподвижную стенку (статор) от потока, увлекаемого вращающимся диском

Nu = 0,297Re⁰ _ω ^,5Pr^0,5 ×

× ( 23,38Pr^0,66 - 8,3Pr - 22,19Pr^0,33 + 10 ) ^0,5 .    (19)

Локальный коэффициент теплоотдачи в стенку диска, вращающегося в потоке, закрученном по закону твердого тела

Nu = 0,23Re⁰ _ω ^,5Pr^0,5 ×

× ( 23,38Pr^0,66 - 8,3Pr - 22,19Pr^0,33 + 10 ) ^0,5. (20)

На рис. 2 изображены графические зависимости теорий различных авторов для определения локальных чисел Нуссельта при ламинарном режиме течения в каверне, а также зависимости (19) и (20). Среднее максимальное расхождение зависимости (20) с теориями других авторов при расчете локальной теплоотдачи в стенку вращающегося в каверне диска составляет 0,2 %. Многие авторы рекомендуют при расчете теплоотдачи в неподвижную стенку (статор) использовать зависимости, полученные для случая вращающегося диска. Возможно такой подход применим для случая слившихся пограничных слоев на роторе и статоре. При реализации между пограничными слоями ядра течения, расчет тепловых потоков по зависимости (20) может накладывать существенную ошибку. Среднее максимальное расхождение зависи- мости (19) с теориями других авторов составляет 20 %, что весьма существенно.

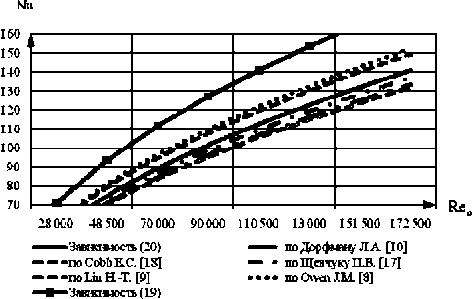
Рис. 2. Сравнение различных теорий для определения локальных чисел Нуссельта при ламинарном режиме течения в каверне газовой турбины

Полученные зависимости применимы для случая вращательного течения в полости между вращающимся диском турбины и корпусом при числах Рейнольдса Re _ω ≤ 1,8 ⋅ 10⁵ [17]. Зависимости применимы для случая, когда ламинарные пограничные слои на статоре и роторе разделяются слоем рабочего тела, в котором влияние вязкости является достаточно малым. Между пограничными слоями находится слой жидкости, который вращается с угловой скоростью, приблизительно равной половине угловой скорости вращения диска [5].