Теплоотдача вращательных течений в турбомашинах на основе двухслойной модели турбулентного пограничного слоя

Течение газового потока для турбонасосных агрегатов (ТНА) носит весьма сложный характер. Поперечный градиент давления оказывает существенное влияние на поверхностное трение и теплообмен. Влияние неучтенных в расчете тепловых нагрузок на узлы и конструкцию может привести к упругим деформациям, а также к нерасчетным параметрам вязкости и плотности рабочего тела, что влечет за собой отклонение от расчетного режима работы агрегата и падение КПД.

Широкое распространение в практике получили методы расчетов по учету теплоотдачи основанные на обобщении экспериментальных данных. Подобные методы показывают удовлетворительные результаты при рассмотрении относительно простых течений. В более сложных условиях, а именно при реализации вращательных течений, зависимости, основанные на обобщении экспериментальных исследований, не применимы, это объясняется достаточно скудными экспериментальными данными в этой области, а также отсутствием точных аналитических решений.

Большие возможности для поиска более точных зависимостей дает теория пограничного слоя. Многочисленными исследованиями установлено, что в большинстве важных для практики тепло- и массооб-мена между поверхностью тела и жидкостью процес- которая получена в предположении, что касательные напряжения полностью определяются как вязкостные, а динамическая скорость в выражении (2), характеризующая собой напряжение трения,

U ■=#, (3)

может быть сопоставлена с потерей напора A h прямолинейного равномерного потока в цилиндрической трубе по формуле

Т о = ^A h Р d,                      (4)

где A h - потеря напора по длине l ; d - диаметр трубы.

Очевидно, что подход определения характеристик через значения напряжения трения весьма трудоемок с точки зрения аналитических выкладок. Выразим динамическую скорость через параметры пограничного слоя. Потребуем, чтобы на границе вязкого подслоя (δ_л) степенной закон (1) сопрягался с линейным законом (2), т. е. при у = 5 _л будем иметь

( U •) ² У ν

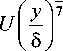
сов основная часть изменения температуры и концентрации также происходит в области, прилегающей к поверхности тела [1].

Рассмотрим частный случай турбулентного течения (Re_m >  3 - 10 5 ) газового потока около вращающе-

Учитывая, что на внешней границе вязкого подслоя

ф _ и §л

ν

= а

л ,

гося диска: распределение скорости ( u ) по толщине пограничного слоя (δ) к скорости в основном потоке ( U ), апроксимируется степенной функцией

где αл – постоянная. Можно записать

«А

.

U*

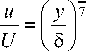
Учтем, что можно выделить несколько зон турбулентного пограничного слоя. В работе [2] опытные данные по замеру профиля скорости соответствуют линейной зависимости

( U •) ² У u =--------, ν

Тогда с учетом (5), (6)

U X = Г ^ал ^v ) ⁷

U   I U *5j

После несложных преобразований выражение для квадрата динамической скорости будет иметь вид

U -V = U i foil)⁴ )   « 2 1⁵ и J

Рассмотрим случай, при котором толщины температурного и динамического пограничных слоев будут одинаковы, т. е. при Pr = 1

Закон теплообмена в виде критерия Стантона для степенного профиля распределения скорости имеет

вид

т - Т 0

Т ₅ — Т о

u

U

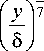
X   д f Т - То I рCpU дУ V Т5- То J

С учетом (8) выражение для определения толщины потери энергии в пограничном слое запишется в виде

О,558 -X-

1        ¹ 4

6   3 е**

^а л ^{- v -5} 1 ф )

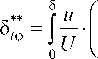
т - Т о Т - Т о

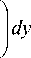
Cp - U ^1/4 - р

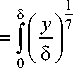
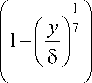
dy = 0,097 -5 .

После упрощения закон теплообмена для турбулентного течения газа имеет вид

X 0,558    1

рCpU0,25 ал,5vо,75 5*ф0,25

Учитывая закон теплообмена

XfдT I q о        =     Vдy J у=о р CpU (Т5 - То) р CpU (Т5 - То)

X р CpU

£f т — т 1" д У I Т ₅ - Т о J.

Следует отметить, что для практического применения закона теплообмена (14) необходимо определить значение а л . Воспользуемся выражением (3):

р( U * )2 =то и выражением для закона трения на плоской пластине при турбулентном обтекании для степенного профиля распределения скорости:

определим производную температурного пограничного слоя на стенке:

^°- = 0,012 56 р U ²

u 5:

**   0’5

£f Т — Т о 1 д У V Т - Т о JI ^У = ^о

_ д f и 1| _ =    1 77 I у=о = дy V U J

тогда выражение (3) примет вид

— fУ17I    =      1 I ду IsJ |y=о 7-51/7 - у6/1 |у=о.

( и * ) ² =^{Т о} = 0,012 56 U ^{2 р}

и 5:

.** Х-0,25

.

ν

Рассмотрим двухслойную модель пограничного слоя, с учетом (1) и (2) в ламинарном подслое имеем

Из условия подобия динамического и температурного пограничных слоев получаем значение производной

тогда

и =( U * )2 У

U v U

_a_f т - Т _о I д У V Т ₅ - Т о J

д f и д У V и

(и • )2 νU ,

,r*V.

д f и 1|    _ д (U ) y I ду V UJIУ=о =дУ   vU   ly=о

окончательно имеем

Af Т - Т _о 1 _ 0,012 56 - и ⁰ ,7 ⁵ д У V Т ₅ - Т о J=   v ⁰ ,75 5 ** ⁰ , ²⁵

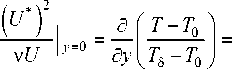
Примем во внимание выражение для динамической скорости (7) и толщины потери энергии температурного пограничного слоя (9), окончательно запишем

Видно, что выражение (12), полученное из условия смыкания ламинарного подслоя с турбулентным профилем при у = 5 _л, и (16), полученное из закона трения степенного турбулентного профиля, имеют сходную форму и отличаются лишь численным коэффициентом. Потребовав равенства производных, определим коэффициент а _л:

Af Т - Т _о I д У V Т ₅ - Т о J

0,558 - U -

1/4

^а л ^-v

V U -5 t _ф J

^а л ^{2 -v}

0,012 56 - U⁰⁷⁵ _v0,75 _-5 **0,25

0,558 - U -

1/4

^а л ^{- v}

V и -5 t ф J

^а л ^{- v}

Лучшее совпадение с полученным значением а л = 12,559 дает значение, полученное в работе [3],

а =

расхождение составляет 10 %; при а _л = 5, получен-

ном в [4], расхождение в 3 раза.

При подстановке (14) в интегральное соотношение уравнения энергии, полученное в [5], учтем что, для вращательного движения (линия тока – кольцевая линия) удобнее выполнить запись в цилиндрических

0,528 -р- Cp • U

Pr5

2 J б ) ⁴ . а 6 • Re _m J

_   „ „      „ - .                ^д H ф ⁵ R 1 .

координатах: ф = а ;; ф = R ; H = R ; ----= — = 1;

^ф дф  д R

д H _ф      д

H = 1; ----= 0; — = 0, тогда будем иметь ф дф дф

^д _**

J Б— о„. д R t ^ф

J Б „**

+ R 6 , . =

X

0,25 Р C p U ,

0,558

^тф I ¹ ^' i

В (23) и (24) J – относительная характерная толщина, полученная в работе [6], б - тангенс угла скоса донной линии тока.

Таким образом, получены зависимости для оценки локального коэффициента теплоотдачи вращательных течений газового потока при различном распределении скоростей; выражения позволяют учитывать локальную температуру движущегося потока, распределение температуры в теплопроводящей стенке, элементарное количество тепла, переданного через единицу поверхности; вывод выражений осуществлялся с учетом подобия температурного и динамического пограничных слоев, что характерно для частного случая Pr = 1.

-..    б **».- ⁵    р C_f ( т , - Т о )

Выражение для определения коэффициента теплоотдачи имеет вид

а = р- Cp • U • St.               (19)

После преобразования (18) с учетом (19) можно записать выражения для определения коэффициента локальной теплоотдачи для вращательных течений газового потока с различным распределением скоростей. Для вращательного течения по закону свободного вихря, с распределением скорости UR = C = const

имеем:

а =

2,18 •р^ Cp • U

Pr5

2 J б ) ⁴ . а 6 • Re _m J

Для вращательного течения, индуцированного вращением диска (закон твердого тела), с распределе-U нием скорости R = ю = const