Теплопроводность городских почв и субстратов почвенных конструкций: методические аспекты и математическое моделирование

Данные о тепловых свойствах почв и субстратов используются в различных прикладных задачах: изучение климата и его изменений (Loukili et al., 2008), выращивание сельскохозяйственных культур (Timlin et al., 2002), исследование продуцирования углекислого газа почвой (Buchner et al., 2008; Bauer et al., 2012) и секвестрации углерода в экосистеме (Ju et al. 2006), изучение структурных и функциональных трансформаций сообществ почвенных микроорганизмов (Glushakova et al., 2020) в связи с различными антропогенными воздействиями (Simsek et al., 2019) и др. Расчет гидротермического режима почв (Ronan et al., 1998; Vogel et al., 2011; Sakai et al., 2011) необходим при использовании климатических моделей (Lin et al., 2018), в грунтоведении, при определении глубины промерзания (Fröb, 2011), при проектировании линейных сооружений (Rajeev et al., 2012), трубопроводов (Zhang, Wang, 2017), изучении пространственной неоднородности структуры почвенного покрова (Yu et al., 2020) и при решении других прикладных задач. Знание тепловых свойств почв требуется в разных областях сельского хозяйства – для разработки мероприятий по защите сельскохозяйственных культур от заморозков (Грингоф, Пасечнюк, 2005), при управлении водными ресурсами, в частности, для планирования норм орошения в засушливых регионах с целью максимального повышения урожайности сельскохозяйственных культур.

В городских условиях остро стоит проблема низкой влаго-обеспеченности газонной растительности в вегетационный период в южных регионах и переувлажнение – в северных. При этом температурный режим в эти периоды также неблагоприятен для растений. Особенно в летний и раннеосенний периоды, когда в поч- вах может наблюдаться иссушение верхнего корнеобитаемого слоя. Это совпадает с периодами повышенных температур в корнеобитаемом слое (для большинства газонных трав температура выше 25 °С является неблагоприятным фактором). Для создания на урбанизированных территориях более оптимальных для газонной растительности гидротермических условий применяются специализированные почвенные конструкции. Они рассчитаны таким образом, чтобы в течение всего вегетационного периода снижать влияние погодных условий на режим температуры и влажности корнеобитаемого слоя почвы. Расчет оптимального соотношения частиц различного размера и качества в почвенных конструкциях (т. е. подбор соотношений различных субстратов или мощностей отдельных слоев) для разных климатических условий включает этап имитационного моделирования. В основе данных рекомендаций лежит предположение, что математические модели способны качественно и адекватно отражать изменения влажности и температуры почв с течением времени. Но это не всегда так, что было показано в ряде работ (Kokoreva, 2021; Weisner, 2016). Так, большое количество математических моделей создано на основе изучения агроландшафтов, а процессы теплопереноса и влагопереноса в сложных почвенных конструкциях изучены слабее (Schjønning, 2021), что приводит к более высоким значениям ошибок при прогнозных расчетах. В то же время для городских территорий (как и для агроландшафтов и естественных территорий) использование возможностей математического моделирования более чем актуально. Это подчеркивает важность экспериментального определения теплофизических параметров почвы в качестве физического обеспечения для целей дальнейшего полифунк-ционального прогнозирования. Однако экспериментальное определение теплофизических свойств почв не всегда возможно, поэтому исследования влияния на термический режим фундаментальных почвенных свойств, таких как плотность, минеральный состав, гранулометрический состав, содержание органического вещества, не теряют актуальности (Сенников и др., 2006). Такие исследования являются основой для получения функциональных зависимостей теплофизических параметров от влажности, поскольку при постоянной температуре влажность в наибольшей степени влияет на тепловые свойства почвы (Arkhangelskaya, Gvozdkova, 2019).

Использование зависимостей тех или иных теплофизических параметров от влажности зависит от уровня модели. При построении глобальных климатических моделей почвы считают гомогенным слоем и используют данные по температуропроводности почвы. В почвоведении же используется иной подход – расчет температурного режима почвы с использованием параметра теплопроводности для каждого слоя почвы. В большинстве одномерных моделей на основе дифференциальных уравнений переноса тепла и влаги в почве используются педотрансферные функции (ПТФ) – регрессионные уравнения, описывающие связь теплопроводности с традиционными химико-физическими свойствами почв: гранулометрическим составом, содержанием органического вещества, плотностью почвы и твердой фазы и др. (Belik et al., 2019). Такой подход реализован в моделях SWAP и HYDRUS-1D. Отличие данных моделей состоит в том, что в SWAP (версия 3.2.34) не предусмотрена возможность управлять зависимостью теплопроводности от влажности Х(0) , в модель встроена единственно возможная регрессионная зависимость, подробно описанная в руководстве (Kroes et al., 2008). Модель HYDRUS-1D (версия 4.17.0140) предлагает выбрать два уравнения Z(0) : Чанга-Хортона и Кэмпбелла (Šejna et al., 2022), – которые достаточно широко распространены в моделировании теплопереноса (Ju et al., 2006; Vogel et al., 2011).

Таким образом, адекватность прогноза и точность в управлении гидротермическим режимом почвы напрямую зависят в первую очередь от наличия качественного экспериментального обеспечения. На данный момент нет единой методики определения тепловых свойств почв и субстратов (Abu-Hamdeh et al., 2000). Так, в России температуропроводность определяют двумя методами: классическим методом регулярного теплового режима и с помощью различных зондовых методик, основанных на методе нестационарного линейного источника тепла (Arkhangelskaya, Gvozdkova, 2019; Болотов, 2003; Макарычев и др., 2010). Однако применение зондовых методов для измерения теплофизических параметров почв ограничено, поэтому изучение особенностей применения зондов в почвенных исследованиях на сегодняшний день является актуальным.

Зондовый метод быстрый и удобный, его можно использовать в полевых условиях (Болотов и др., 2010; Rozanski et al., 2013). Но при использовании зонда чаще всего исследуется не вся кривая зависимости тепловых параметров почвы от влажности, а только конкретная величина теплопроводности при данной влажности. Кроме того, несмотря на то, что прибор K2Dpro и его модификация TEMPOS занесены в Государственный реестр средств измерения РФ, нет достаточной информации методического характера в отечественной и иностранной литературе. Также не до конца ясны вопросы применения полученных характеристик различных почвенных субстратов для целей почвенного конструирования.

В этой статье рассмотрены методические особенности проведения оценки теплопроводности различных городских почв и субстратов методом линейного источника тепла. Проведена оценка чувствительности теплопроводности к ряду физических характеристик образцов. Описана возможность получения зависимости теплопроводности от влажности для субстратов, используемых в почвенном конструировании. Проведено сравнение значений теплопроводности, полученных на основе аппроксимации экспериментальных данных и на основе педотрансферных функций.

ОБЪЕКТЫ И МЕТОДЫ

Для исследования были выбраны гумусовые горизонты зональных городских почв (Москва, Краснодар, Волгоград, соответствующих ряду: дерново-подзолистая почва, чернозем, каштановая почва), имеющих одинаковый возраст 60–70 лет:

• 1)    урбостратозем среднемощный, глубоко слабооглеенный, среднесуглинистый на техногенных отложениях, подстилаемых покровным суглинком на территории Москвы;

• 2)    урбочернозем миграционно-сегрегационный тяжелосуглинистый на карбонатных лёссовидных суглинках на территории Краснодара;

• 3)    урбосветлогумусовая аккумулятивно-карбонатная сегрегационная стратифицированная глубокосолончаковатая почва среднесуглинистая на морских отложениях в Поволжском регионе.

В качестве субстратов для создания конструктоземов были использованы:

• 1)    верхний слой урбанозема территории МГУ имени М.В. Ломоносова, г. Москва;

• 2)    торф низинный “Селигер-Агро”, г. Москва (далее – торф);

• 3)    песок карьерный (производитель Русеал), г. Москва (далее – песок);

• 4)    смесь горизонта  А пах   (Москва), торфа низинного

(Москва) и песка карьерного (Москва) (далее – смесь). Соотношение субстратов по абсолютно сухой массе в смеси равно: А пах : торф : песок = 4.4 : 1 : 5.9.

Физические свойства естественных почв и субстратов приведены в таблице 1.

Физические свойства почвы определялись традиционными методами (McKenzie, 2002; Шеин, Карпачевский, 2007). В полевых условиях была определена плотность естественной почвы буровым методом, а плотность насыпных образцов задавалась в соответствии с рекомендациями (Сусленкова и др., 2018). В насыпных образцах определен гранулометрический состав методом лазерной дифракции с использованием лазерного анализатора размера частиц Mastersizer 3000e (Malvern Panalytical, UK) и содержание органического углерода методом сжигания в токе кислорода на экспресс-анализаторе углерода АН–8012. Удельная поверхность по азоту была измерена на аналитическом комплексе для определения текстурных характеристик дисперсных систем (Vapor 100, Meso 222, 3P INSTRUMENTS, Германия).

Теплопроводность определялась методом нестационарного линейного источника тепла с помощью прибора TEMPOS, который входит в Государственный реестр средств измерения РФ.

Таблица 1. Некоторые физические и химические свойства исследованных почв и субстратов

Table 1. Some physical and chemical properties of the studied soils and substrates

Образец, глубина, см	Среднее распределение частиц по размерам				Объемная плотность, (г/см3)	и	Удельная поверхность по азоту, м2/г
	Песок	Пыль	Глина	Текстурный класс
	2–0.05	0.05–0.002	<0.002
Дерновоподзолистая	17.9	72.9	9.2	пылеватый суглинок	1.01	3.10	8.31
Чернозем	0.5	80.2	19.3	пылеватый суглинок	1.23	4.92	5.95
Каштановая	15.9	68.1	16.0	пылеватый суглинок	1.38	1.38	9.05
Песок	88.9	8.4	2.7	песок	1.60	0.38	0.55
Торф	-	-	-	торф	0.27	89.9	1.45
Смесь	6.5	65.1	28.4	пылеватый суглинок	1.01	1.01	2.41

Как и для любого прибора, основанного на импульсном методе, в TEMPOS реализован принцип максимума температуры исследуемой точки среды после того, как действие источника тепла прекращается. Время наступления и величина этого максимума зависят от теплофизических параметров, которые определяются на основе решения уравнения Фурье с известными граничными условиями (Болотов, 2003). Метод позволяет избежать больших ошибок при измерении тепловых свойств почв и других материалов, а также сократить время проведения эксперимента (Campbell et al, 1994).

Прибор TEMPOS состоит из портативного контроллера и датчика (в комплекте 4 датчика, не все подходят для почв), называемого игольчатым зондом. Теплопроводность вычисляется через измерение рассеивания тепла от игольчатого зонда. Точность измерения температуры прибором TEMPOS, в соответствии со спецификацией, составляет 0.001 °С, поэтому в дополнительной калибровке прибора нет необходимости. Однако калибровки требуют зонды. Для исследования использовался зонд SH-3 (с двумя иглами – щупами – длиной 30 мм и диаметром 1.3 мм), верификация которого выполнялась на блоке синтетического материала Delrin с известными тепловыми характеристиками при заданной температуре. При верификации данного зонда рекомендуется оставлять щупы в материале на 15 минут для установления теплового равновесия между материалом и щупами (Келле, 2020).

Принцип работы зонда SH-3 заключается в том, что иглы зонда в течение первых 30 секунд приходят в состояние теплового равновесия со слоем почвы. За это время прибор TEMPOS собирает данные для расчета температурного дрейфа. Если дрейф ниже граничного значения (<0.002 °С), ток подается к одной из игл зонда в течение следующих 30 секунд для нагрева. Другая игла, расположенная на расстоянии 6 мм от первой, регистрирует температуру окружающей среды. После завершения подачи тока на первую иглу температура фиксируется еще в течение 90 секунд, за которые происходит охлаждение первой иглы. Изменение температуры иглы зонда SH-3 (ΔT) далее рассчитывается по уравнениям (1) и (2):

4т = Ш*и(-4б;), при ®-                  (1)

^4T =Ш • < ^EI •    ' ^- Ei [(-4Э- при t>t h (2)

где:

ΔT – рост температуры во второй игле (°С), q – количество тепла, подводимого к первой игле (Вт/м), k – теплопроводность (Вт/м*K), r – расстояние между двумя иглами (мм),

D – температуропроводность, (мм²/сек), t – время общее (секунды), t h – время нагрева (секунды),

Ei – экспоненциальный интеграл (Келле, 2020).

Данные по температуре аппроксимируются экспоненциальной интегральной функцией с использованием нелинейного метода наименьших квадратов (O’Donnell et al., 2009). С помощью данного метода, по заданным значениям q, r, t и t h , рассчитываются теплопроводность (k) и температуропроводность (D). Теплоемкость рассчитывается как коэффициент пропорциональности между теплопроводностью и температуропроводностью.

При измерении теплофизических характеристик к зонду SH-3 предъявляется обязательное требование – соблюдать расстояние 1.5 см от края образца во всех трех измерениях (Келле, 2020).

Данный зондовый метод имеет ограничения, связанные, прежде всего, с отличиями от модели так называемого “идеального” зонда (длина превышает диаметр в 100 раз и находится в плотном контакте с материалом) и идеальных внешних условий (во время проведения эксперимента предполагается, что состав, структура и внешняя температура образца не меняются). Наиболее существенными отличиями реальных зондов от идеальных являются следующие: (1) температура окружающей среды не постоянна, что будет влиять на показания прибора (Liu et al., 2011); (2) в почве, не полностью насыщенной водой, при нагревании будет происходить перераспределение влаги от теплого участка к более холодному. Последнее отличие накладывает ограничения на быстрое измерение в нескольких повторностях при стационарной установке зонда, а проведение измерений в разных местах матери- ала приводит к образованию дополнительных полостей в нем, создавая дополнительное контактное сопротивление между зондом и материалом.

Поскольку для почв применение зондовых методов имеет ряд особенностей (Болотов и др., 2010), необходимо прежде всего сказать о некоторых обнаруженных методических аспектах работы с прибором. Когда явление температурного дрейфа при слишком большом перепаде температур при нагреве иглы (˃0.002 °С) приводит к возникновению ошибки, это, по результатам исследования, связано с пористостью объекта, так как в более пористом материале иглы зонда будут соприкасаться и с воздухом, и непосредственно с измеряемым материалом. Это особенно часто наблюдалось в высокопористых почвах, таких как монолиты минеральных почв среднесуглинистого состава. При этом с уменьшением влажности суглинка частота возникновения температурного дрейфа существенно возрастала, т. к. увеличивалась вероятность контакта игл с воздухом. В песчаных образцах явление дрейфа часто появлялось только при достаточно низких значениях влажности. При возникновении дрейфа измерение повторяли после некоторой паузы.

Измерения теплопроводности были проведены в насыпных почвенных образцах заданной плотности, помещенных в пластиковые цилиндры высотой 5 см и диаметром 8.5 см. Для убрастра-тозема (Москва) использованы также монолитные образцы того же размера. Размер образцов обусловлен особенностями метода определения теплопроводности.

Для выявления степени влияния условий проведения измерений на величину теплопроводности почвенных образцов были реализованы следующие варианты измерения теплопроводности:

• 1)    в дерново-подзолистой почве в диапазоне температуры образца 19–33 °С;

• 2)    в колеблющемся стандартном образце;

• 3)    в стандартном и почвенных образцах непосредственно после установки зонда и после 15-минутной паузы;

• 4)    в процессе иссушения почвенных образцов при стационарной установке и фиксации зонда с извлечением зонда после каждого измерения;

• 5)    в образцах дерново-подзолистой почвы, торфа и песка без стационарной установки зонда в 9 повторностях (1 точка в центре монолита, 8 точек – равномерно по окружности с отступом от края монолита 1.5 см) при нескольких значениях влажности в диапазоне от полной влагоемкости (ПВ) до гигроскопической влажности (ГВ) (рис. 1);

• 6)    в образцах почв и субстратов в процессе иссушения;

• 7)    в образцах почвы с различной плотностью;

• 8)    в образцах с различной степенью соприкосновения иглы и твердого материала (размер отверстий задавался).

Проверка гипотезы о нормальности распределения значений теплопроводности осуществлялась с помощью критерия Уилкса– Шапиро.

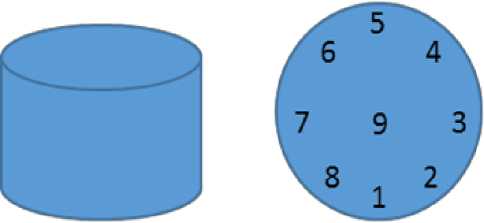
Рис. 1. Схема установки зонда SH-3 в 9 точках почвенного монолита. Fig. 1. Scheme of installing the SH3 probe at 9 points of a soil monolith.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Методические аспекты

Влияние общих условий проведения измерений

Согласно техническому описанию прибора (Келле, 2020), зонд SH-3 при верификации на стандартном материале рекомендуется оставлять на 15 минут перед измерением, а поверку проводить при стандартной температуре 21 °С без механического воздействия на образец. Однако при колебаниях температур образца от 9 до 35 °С повышение температуры стандартного образца и/или почвенного монолита не всегда приводило к заметному изменению теплопроводности. Так при охлаждении поверочного блока Delrin теплопроводность изменялась от заявленных 0.38 Вт/(м*К) при 21 °С до 0.370 Вт/(м*К) при 9 °С при заявленной погрешности измерения теплопроводности ±10% в диапазоне 0.2–2 Вт/(м*К) (Келле, 2020). Изменения теплопроводности с изменением температуры почвенного образца более значимы (рис. 2) – при изменении температуры на 15 °С теплопроводность увеличивается более чем на 30%. При полевых исследованиях и сравнении почв в периоды с различными погодными условиями возможны значительные расхождения в показаниях – как при исследованиях контрастных температур в почве, например, при лесных пожарах (Dymov et al., 2022), так и при сезонных колебаниях теплопроводности в почвах.

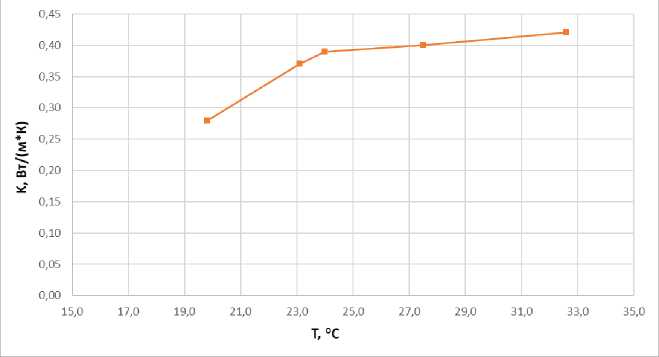
Рис. 2. Влияние температуры (Т) образца дерново-подзолистой почвы на полученные с использованием прибора TEMPOS (зонд SH-3) показания теплопроводности.

Fig. 2. Effect of sod-podzolic soil sample temperature (T) on thermal conductivity readings obtained using the TEMPOS device (probe SH-3).

При физическом воздействии (колебание стандартного образца) теплопроводность возрастала с 0.380 до 0.410 Вт/(м*К), что может приводить к значимым ошибкам определения теплопроводности (как и других теплофизических параметров). Напротив, несоблюдение рекомендации времени, необходимого для выравнивания температуры зонда и образца (15 минут), давало некоторую погрешность для стандартного образца, но практически не влияло на показания в почвах и субстратах, где разброс показаний теплопроводности был значительнее, чем погрешность измерения.

Влияние способа установки зонда

Для почвенного образца определяющую роль играл способ установки зонда во влажном образце или размещение зонда в сухом и/или плотном образце (высокое сопротивление материала при установке / необходимость готовых отверстий для зонда). Во влажном образце есть вероятность повреждения места установки зонда во время манипуляций с прибором, что уменьшит контакт игл зонда с поверхностью почвы. В плотном образце необходимо просверливать отверстия для зонда, что также увеличивает вероятность большего контакта игл с воздухом, а не с поверхностью почвы (табл. 2). Частично эта проблема решается использованием различных термопаст. Но для надежного контакта зонда и почвы более стабильные результаты дала стационарная установка зонда в монолит или насыпной образец на весь период иссушения образца с надежной фиксацией зонда в образце, чтобы при манипуляциях с образцом или прибором не происходило увеличение диаметра отверстий, в которые вставлен зонд. Для этого были использованы клейкая лента или силиконовая крышка с отверстием для зонда, вставляемого в монолит.

Как видно из таблицы, при воздушно-сухом состоянии почвы диаметр отверстий, т. е. степень прилегания игл зонда к почвенным образцам, не влияет на сыпучие (песок) и слабо влияет на упругие (торф) материалы, но играет значительную роль в плотных минеральных субстратах, где трещины будут только расти при механическом воздействии зонда на материал почвенного образца.

Таблица 2. Зависимость λ(θ) от плотности прилегания зонда SH-3 к почвенному образцу

Table 2. Dependence of λ(θ) on the tightness of SH-3 probe adjoining to the soil sample

	Теплопроводность, Вт/(м*К)
	воздушно-сухая почва				почва при капиллярном насыщении
диаметр отверстий для зонда SH-3	суглинок	торф	песок	смесь	суглинок	торф	песок	смесь
1.4 см	0.280	0.093	0.240	0.260	0.790	0.520	3.010	1.480
2.4 см	0.210	0.092	0.230	0.250	0.750	0.360	2.070	1.450
3.1 см	0.180	0.093	0.230	0.240	0.730	0.310	1.610	1.190

В увлажненных образцах влияние степени прилегания зонда к поверхности материала проявилось для всех почвенных образцов даже при небольшом увеличении отверстий для зонда, что особенно вероятно во влажном песке даже при небольшом колебании зонда во время измерения.

Поэтому были испытаны два варианта измерения теплопроводности в монолите из дерново-подзолистой почвы, взятом на территории г. Москва. Вариант 1: зонд вынимался из образца после измерения и устанавливался заново перед следующим измерением. Вариант 2: зонд установлен в почву стационарно и не извлекался во время всего периода иссушения.

Из данных таблицы 3 следует, что для суглинистой почвы наблюдалось наибольшее расхождение показаний теплопроводности, что может быть связано как с установкой зонда, так и с особенностями порового пространства. Это позволяет рекомендовать использование стационарного метода установки зонда.

Однако при сравнении кривой, полученной при равновесном иссушении со стационарно установленным зондом, и точек, полученных при разовых установках зонда, соблюдаются общие закономерности изменения теплопроводности при уменьшении влажности образца (рис. 3).

Это позволяет использовать данный способ работы с прибором в условиях, когда необходимо сократить время измерения тепловых свойств, что может стать критичным при исследованиях больших партий образцов.

Статистические характеристики варьирования значений теплопроводности

Определение теплопроводности в образцах без стационарной установки зонда возможно в повторностях, что позволяет оценить зависимость статистических характеристик варьирования теплопроводности от влажности (табл. 4). При уровне значимости 0.05 значения теплопроводности можно считать нормально распределенными (Дмитриев, 2009).

Таблица 3. Зависимость λ(θ) для суглинка, песка и торфа в двух вариантах установки зонда (пояснения в тексте) Table 3. Dependence of λ(θ) for loam, sand and peat on 2 variants of probe installation (explanations are given in the text)

Категории почвенной влаги	суглинок		песок		торф
	вариант 1	вариант 2	вариант 1	вариант 2	вариант 1	вариант 2
ПВ	0.887	1.193	2.690	3.022	0.558	0.573
НВ*	0.914	1.193	2.899	2.845	0.561	0.542
0.7×НВ	0.704	1.055	2.905	2.488	0.405	0.317
ГВ	0.234	0.531	0.271	0.364	0.127	0.098

Примечание. *НВ – наименьшая влагоемкость.

Note. *НВ – field water holding capacity.

Таблица 4. Зависимость статистических характеристик варьирования значений теплопроводности изученных почв от влажности

Table 4. Dependence of statistical characteristics of variation of thermal conductivity values of the studied soils on moisture content

Почва	Влажность, %	Объем выборки	X , Вт/(м*К)	S, Вт/(м*К)	SX, Вт/(м*К)	V, %
	4.7	9	0.319	0.055	0.018	17
	46.4	9	0.919	0.147	0.049	16
суглинок	55.0	9	1.023	0.092	0.031	9
	58.3	9	1.060	0.082	0.027	8
	0.0	9	0.269	0.011	0.004	4
песок	26.0	9	2.838	0.067	0.022	2
	31.2	9	2.726	0.115	0.038	4
	32.4	9	2.765	0.085	0.028	3
	1.8	9	0.130	0.015	0.005	12
	22.8	9	0.235	0.020	0.007	9
торф	71.1	9	0.542	0.045	0.015	8
	78.3	9	0.558	0.022	0.007	4
	84.9	9	0.561	0.006	0.002	1

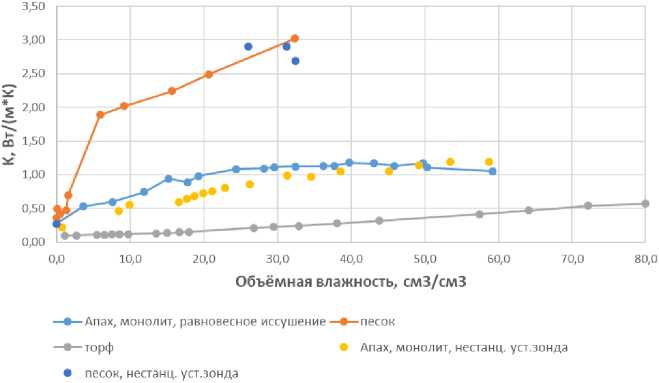
Рис. 3. Сравнение данных по зависимости теплопроводности от объёмной влажности почвы/субстрата λ(θ) для стационарно и не стационарно установленных зондов.

Fig. 3. Comparison of data on the dependence of thermal conductivity on the volumetric soil/substrate moisture λ(θ) for stationary and non-stationary installed probes.

С ростом влажности наблюдается увеличение стандартного отклонения с максимумом значений в диапазоне капиллярной влажности, при которой часть порового пространства почв занята водой, а часть – воздухом. Минимальные значения стандартного отклонения получены для всех образцов при ГВ, а также для торфа при влажности, соответствующей ПВ, максимальные – для значений влажности, близких к капиллярной влагоемкости (КВ). Наиболее высокие коэффициенты вариации характерны для суглинка. При этом по мере увеличения влажности коэффициенты вариации уменьшаются. Среди вероятных причин различий в характере варьирования значений теплопроводности изученных образцов можно назвать степень дифференциации порового пространства, которая определяет неравномерность распределения влаги и воздуха и наиболее выражена в почвах суглинистого ряда.

Следует также отметить, что в диапазоне капиллярной влажности почвы суглинистого ряда наиболее подвержены пластическим деформациям при внешнем воздействии. Предполагаем, что при установке зонда суглинистая почва деформируется, что снижает плотность прилегания почвы к поверхности зонда и приводит к увеличению варьирования значений теплопроводности. Торф и песок, в отличие от суглинка, проявляют признаки упругости, что создает условия для плотного контакта с поверхностью зонда.

Влияние свойств почвы на величину теплопроводности Зависимость теплопроводности от влажности

Для зонального ряда почв (рис. 4) при ГВ теплопроводность наименьшая для всех трех типов почв (дерново-подзолистая почва – 0.229 Вт/(м*К), чернозем – 0.308 Вт/(м*К), каштановая почва – 0.222 Вт/(м*К)). С повышением степени увлажнения почвы от ГВ до КВ в большей степени увеличивается теплопроводность у дерново-подзолистой почвы, несколько медленнее – у каштановой почвы, однако в целом колебания теплопроводности для трех почв не превышают 0.500 Вт/(м*К). При КВ наибольшая теплопроводность наблюдается у дерново-подзолистой почвы – 1.430 Вт/(м*К), у каштановой почвы она меньше – 1.282 Вт/(м*К) и наименьшая теплоемкость наблюдается у чернозема – 1.007 Вт/(м*К). При дальнейшем насыщении почвенных образцов до ПВ их теплопроводность несколько уменьшается, за исключением чернозема, у которого она слабо возрастает. При достижении ПВ теплопроводность чернозема равна 1.103 Вт/(м*К), каштановой почвы – 1.260 Вт/(м*К), дерново-подзолистой почвы – 1.314 Вт/(м*К).

Для субстратов почвенных конструкций при ГВ теплопроводность составляет 0.229 Вт/(м*К) для суглинка, 0.234 Вт/(м*К) для смеси, 0.250 Вт/(м*К) для торфа и 0.280 Вт/(м*К) для песка. При увеличении содержания влаги в почве скорость увеличения теплопроводности выше для песчаного субстрата, и при КВ величина его теплопроводности выше по сравнению с теплопроводностью других субстратов. Вероятно, это связано с минералогическим составом (теплопроводность кварца при 20 °С составляет 0.389 Вт/(м*К)) и плотностью песка (1.73 г/см3), которая повыша- ет его теплопроводность.

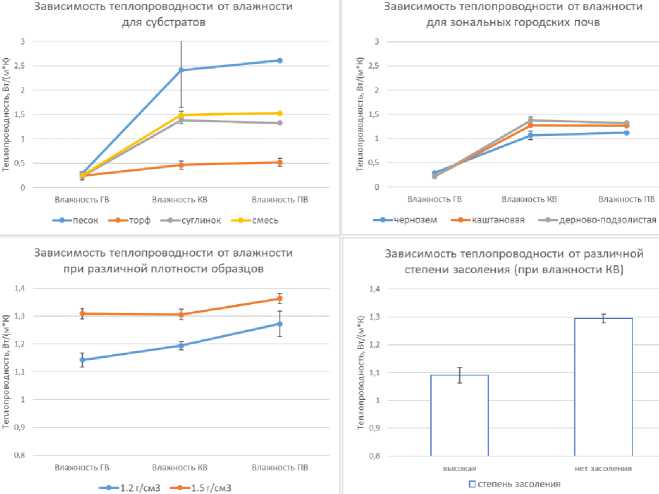
Рис. 4. Диаграммы зависимости теплопроводности от влажности λ(θ) и степени засоления городских почв и субстратов.

Fig. 4. Diagrams of the dependence of thermal conductivity on humidity λ(θ) and the degree of urban soils and substrates salinity.

При КВ теплопроводности смеси и суглинка имеют близкие значения, что будет играть роль в северных регионах страны, где наблюдаются частые случаи переувлажнения городских почв вследствие обильных осадков. Теплопроводность торфа при увеличении влажности субстрата увеличивается наиболее медленно, что связано с преимущественно органической составляющей субстрата. При достижении КВ теплопроводность песка составляет 1.865 Вт/(м*К), суглинка и смеси – соответственно 1.430 и 1.361 Вт/(м*К), торфа – 0.412 Вт/(м*К). С дальнейшим увеличением содержания влаги до ПВ теплопроводность песка продолжает мед- ленно увеличиваться. Теплопроводность суглинка несколько снижается, а теплопроводность смеси несколько увеличивается. Для торфа на всем протяжении кривой зависимости λ(θ) теплопроводность изменяется наиболее слабо по сравнению с другими субстратами. При ПВ теплопроводность песка составляет 2.605 Вт/(м*К), суглинка и смеси – 1.314 и 1.568 Вт/(м*К) соответственно, теплопроводность торфа – 0.521 Вт/(м*К).

Более подробные кривые зависимости теплопроводности от влажности субстратов и монолитов верхнего горизонта урбанозе-ма представлены на рисунке 5. Для насыпных образцов не удалось зафиксировать увеличение теплопроводности в диапазоне КВ. Возможно, это связано с методом измерения теплопроводности: некоторое увеличение наблюдается только для образца при равновесном способе иссушения, когда при каждой влажности производилось влагостатирование образца. У остальных образцов исследование теплопроводности проводилось одновременно с исследованием кривой влагоудержания методом испарения. Некоторое отличие теплопроводности в насыпном образце и в монолите наблюдается для суглинка в области высоких значений влажности (до 0.2 Вт/(м*К)).

Изменение λ(θ) в процессе иссушения наиболее слабо выражено у торфа (постепенное снижение от 0.6 до 0.2 Вт/(м*К)). Наиболее резкая кривая λ(θ) у песка, при этом для песка в диапазоне от 32 до 5% влажности теплопроводность изменяется равномерно (от 3.0 до 1.8 Вт/(м*К)), а потом наблюдается резкое падение теплопроводности до значений 0.4 Вт/(м*К). Наиболее интересная λ(θ) получена для образца смеси (суглинок, торф, песок). Для влажного образца смеси теплопроводность находится на уровне суглинка (1.3 Вт/(м*К)), а после 30% влажности она резко снижается до 0.6 Вт/(м*К) и повторяет кривую торфа. Следовательно, тепловые свойства торфа в составе смеси в сухой области кривой влагоудержания проявляются в большей степени, чем тепловые свойства других компонентов смеси.

Таким образом, влажность в наибольшей мере определяет тепловые свойства почв при заданной температуре, а количество и качественные характеристики воды играют определяющую роль в значениях теплопроводности почв и субстратов. Помимо влажно- сти, температуры и минералогического состава, были рассмотрены и менее значимые, но важные свойства: плотность, гранулометрический состав и наличие легкорастворимых солей (рис. 4).

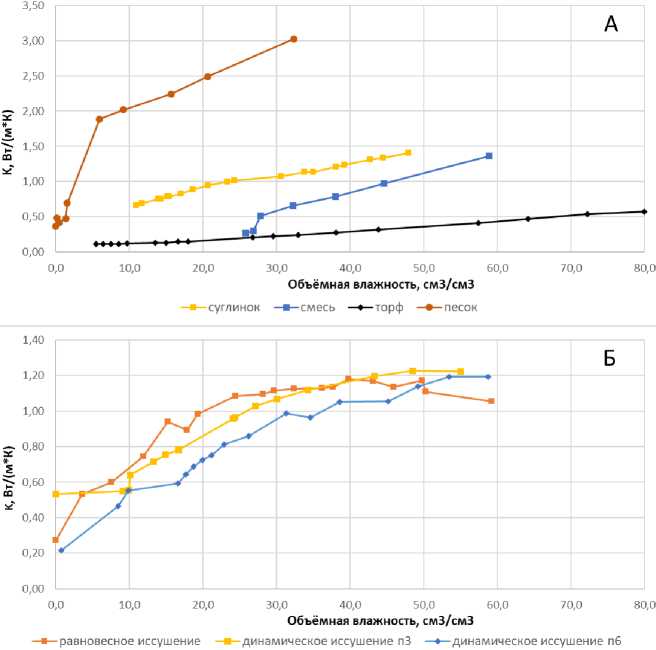
Рис. 5. Зависимости теплопроводности от объемной влажности для субстратов ( А ) и урбостратозема, Москва ( Б ).

Fig. 5. Dependences of thermal conductivity on volumetric humidity for substrates ( A ) and urban stratozem, Moscow ( Б ).

Зависимость теплопроводности от плотности почвы

Выбранные значения влажности субстратов (ПВ, КВ, ГВ)

унифицируют влияние влажности, поскольку именно категории влаги формируют зависимость λ(θ). При ГВ теплопроводность дерново-подзолистой почвы с низкой плотностью (1.2 г/см3) составляет 1.142 Вт/(м*К), а теплопроводность этой же почвы с высокой плотностью (1.5 г/см3) составляет 1.309 Вт/(м*К). При повышении содержания влаги в почве от ГВ до КВ теплопроводность почвы с низкой плотностью увеличивается, а теплопроводность почвы с высокой плотностью практически не изменяется с трендом к незначительному уменьшению. При КВ теплопроводности почв с низкой и высокой плотностью равны соответственно 1.194 и 1.305 Вт/(м*К), а при полном насыщении теплопроводность дерново-подзолистой почвы с низкой плотностью равна 1.272 Вт/(м*К), а теплопроводность образца с высокой плотностью – 1.363 Вт/(м*К), что не является значимым различием в пределах выборки.

Влияние гранулометрического состава и удельной поверхности на теплопроводность

Анализ приведенных зависимостей λ(θ) позволяет заключить, что гранулометрический состав существенно влияет, и даже определяет значение теплопроводности субстратов. При крупном размере зерен (частиц почвы) доступное поровое пространство будет выше (из-за присутствия воздуха), что приведет к более низкой теплопроводности почвы. Следовательно, плотные поч-вы/субстраты во всем диапазоне влажности имеют более высокие значения теплопроводности. Поэтому при выборе плотности закладки субстратов в процессе конструирования почв необходимо учитывать, что менее плотные слои будут подвержены большим колебаниям температур при одинаковых погодных условиях (в статичных условиях, поскольку в процессе функционирования свойства отдельных слоев почвенных конструкций будут изменяться).

Удельная поверхность также является приоритетным свойством для описания тепловых характеристик почв/субстратов. Ранее (Гюлалыев, 2015) отмечалась зависимость температуропроводности от удельной поверхности, данные этого исследования подтвердили рост теплопроводности с увеличением удельной по- верхности почв: вода образует пленку на поверхности частиц почвы, это снижает теплопроводность.

Зависимость теплопроводности от наличия в субстратах легкорастворимых солей

Теплопроводность суглинка снизилась (рис. 4) с увеличением концентрации солей (с 1.3 Вт/(м*К) до 1.1 Вт/(м*К)). В опыте была использована соль KBr, более 15 мСм/м, что соответствует высокой степени засоления). Это согласуется с результатами Ноборио и Макиннеса (1993) для NaCl. Основная часть брома хорошо растворима, что характеризует засоленную почву как более дисперсионный материал, обладающий высокой теплопроводностью. Для почв со значительным количеством тонких частиц (су-глинок/глина) агрегация будет сильно зависеть от взаимодействия самых тонких почвенных частиц с ионами соли. Чем менее упорядочена такая структура, тем ниже теплопроводность.

Экспериментальное обеспечение прогнозных моделей

Полученные кривые зависимости λ(θ) для почв и субстратов можно использовать в качестве экспериментального обеспечения в моделях типа HYDRUS-1D. Наиболее полный обзор функциональных моделей для λ(θ) представлен в исследовании (Zhang, Wang, 2017), где рассмотрены уравнения регрессии для прогнозирования теплопроводности на основе легко измеряемых величин, а также соотношения воды и воздуха в поровом пространстве почвы. Однако для модели HYDRUS-1D не предусмотрена возможность задания λ(θ) иным способом, кроме как с помощью уравнений Чанга–Хортона и Кэмпбелла. Для этого необходимо аппроксимировать полученные экспериментальные кривые λ(θ) одной из функций и задать полученные параметры аппроксимации в качестве входных данных модели HYDRUS-1D.

В нашем исследовании в качестве примера возможного прикладного применения экспериментально определенных зависимостей λ(θ) эти кривые одинаково успешно аппроксимированы для всех использованных субстратов: суглинок, торф, песок, смесь (рис. 6).

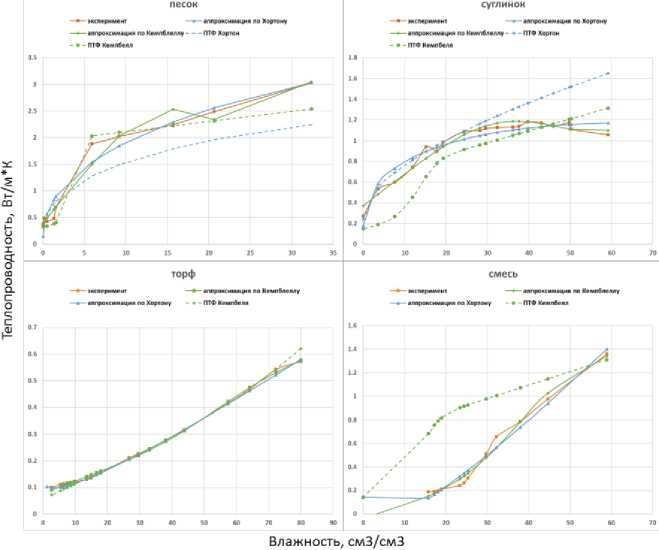
Рис. 6. Экспериментальные кривые зависимости теплопроводности от объёмной влажности, аппроксимации экспериментальных кривых уравнениями Кэмпбелла и Чанга–Хортона, а также кривые, рассчитанные с использованием педотрансферных функций (также использованы функциональные зависимости Кэмпбелла и Чанга– Хортона, рекомендованные авторами HYDRUS).

Fig. 6. Experimental curves of the thermal conductivity dependence on volumetric humidity, approximations of experimental curves by the Campbell and Chang–Horton equations (the Campbell and Chang–Horton functional dependences, recommended by the authors of HYDRUS, are also used).

Встроенные в модель педотрансферные функции позволили рассчитать зависимости λ(θ), которые были сопоставлены с полученными экспериментальными кривыми. Педотрансферные функции в модели HYDRUS-1D позволяют использовать зависимости λ(θ), опубликованные в работе (Chung, Horton, 1987), подробно обсуждаемые во многих исследованиях (Arkhangelskaya, Gvozdko-va, 2019; Buchner et al., 2008; Bauer et al., 2012; Sakai et al., 2011).

Модель Чанга–Хортона для расчета зависимости теплопроводности от влажности почв и субстратов имеет вид:

λ0(θ) = b1 + b2θ + b3θ0.5, где θ – объемная влажность почвы (см3/см3), b1, b2, b3 – эмпирические коэффициенты.

Существенным недостатком этой модели явилось то, что авторы использовали только три текстурных класса (глина, суглинок, песок). Поэтому для задачи сравнения λ(θ) различных, но находящихся в одном текстурном классе, почв или восстановления λ(θ) для органических почв и субстратов на их основе данная модель не подходит, т. е. выполнить расчет температурного режима, например, почвенной конструкции только на основе данных о гранулометрическом составе невозможно. Альтернативой является получение экспериментальных данных, которые могут быть аппроксимированы данным уравнением, а параметры аппроксимации могут быть использованы в качестве физического обеспечения модели HYDRUS-1D.

Но даже для тех субстратов (суглинок, песок), для которых расчет λ(θ) через педотрансферные функции по модели Чанга– Хортона возможен, не удалось получить удовлетворительный результат. Расчетные кривые значительно отличаются от экспериментальных (для суглинка, при влажности 30–60%, модель переоценила теплопроводность, для песка – недооценка теплопроводности во всем диапазоне влажности).

Уравнение Кэмпбелла использует данные о плотности почвы, содержании фракции глины (менее 0.05 мм), данные о минералогическом составе почвы (Campbell, 1994):

λ 0 (θ) = A+ Bθ- (A - D)exp [-(Cθ) ^K ]

0.57 + 1.73θ + 0.93θ

A=

1 - 0.74θq q- 0.49θmm - 2.8θn(1 - θn)

B = 2.8θ n

C = 1 + 2.6θ_c ^-1/2

D = 0.03 + 0.7θ ² n

E=4

где λ 0 – теплопроводность, Вт/(м*К);

• θ – объемная влажность, м³/м³;

• θ n – объемная влажность твердого вещества, м³/м³;

• θ q – объемная влажность кварца, м³/м³;

• θ c – объемная влажность глины, м³/м³;

• θ m – объемная влажность других минералов, м³/м³.

0.6 Вт/(м*К)).

Модель Кэмпбелла позволяет рассчитывать любые варианты городских субстратов с использованием ПТФ на основе содержания кварца и других минералов, общей пористости, плотности почвы (заданной плотности субстратов). Однако только для торфа расчет теплопроводности через ПТФ по модели Кэмпбелла прошел успешно. Для песка расчетная кривая существенно отличается от экспериментальной кривой в области влажностей выше НВ (на 0.5 Вт/(м*К)), а для суглинка наибольшая ошибка (до 0.3 Вт/(м*К)), наоборот, находится в области 0–20% объемной влажности.

Для образца смеси, включающего все три субстрата, моделирование теплопроводности по Кэмпбеллу было наименее удачным. Расчетная кривая только при ПВ совпала с экспериментальной, во всем остальном диапазоне расчетная кривая существенно завышает теплопроводность (при влажности 20%  – на

Таким образом, для нашей выборки образцов модель Кэмпбелла позволяет задавать теплофизические свойства почв и субстратов через ПТФ при отсутствии экспериментальных данных. Однако для нестандартных субстратов (органо-минеральные смеси) решение обратной задачи (восстановление кривой λ(θ)) все же требует экспериментальных данных о теплопроводности почв, которые будут являться необходимым экспериментальным обеспечением при адекватной аппроксимации.

ВЫВОДЫ

• 1.    Для получения кривых зависимости теплопроводности от влажности почв необходим ряд методических рекомендаций. В зависимости от целей и необходимой степени точности исследования возможны различные варианты использования прибора: 1) использовать монолитные образцы для исследования λ(θ) и фиксировать зонд в образце в течение всего периода иссушения почвенного образца, 2) задавать влажность для каждой точки на кривой зависимости λ(θ), или 3) увеличивать число повторностей при исследовании λ(θ) в одном образце, особенно для минеральных почв.

• 2.    При исследовании влияния химико-физических свойств на величину теплопроводности, определяющих теплофизические свойства субстратов для городских конструктоземов и верхних горизонтов городских почв, выявлен ряд закономерностей:

• -    в монолитных почвенных образцах с более неоднородным поровым пространством теплопроводность несколько ниже по сравнению с насыпными образцами (до 0.2 Вт/(м*К)), что объясняется более быстрым переносом тепла в выровненном поровом пространстве насыпных образцов.

• -    теплопроводность почв и субстратов зависит от влажности в наибольшей степени. Разброс значений теплопроводности в диапазоне от гигроскопической влажности до полной влагоемкости для дерново-подзолистой почвы составляет 0.229–1.430 Вт/(м*К), для торфа разброс составляет 0.250–0.521 Вт/(м*К), для песка 0.280–2.605 Вт/(м*К), для смеси 0.234–1.568 Вт/(м*К).

• -    при заданной влажности почва с более низкой плотностью (1.2 г/см³) обладает меньшей теплопроводностью, чем почва с более высокой плотностью (1.5 г/см³) – 1.142–1.272 Вт/(м*К) и 1.305–1.363 Вт/(м*К) соответственно. Это согласуется с большим объемом воды или воздуха в менее плотной почве, которые имеют меньшие значения теплопроводности, чем твердая фаза минеральных почв.

• -    при увеличении содержания органического вещества теплопроводность почв уменьшается, что определяет как тепловые свойства высокогумусных минеральных почв (чернозема), так и орга-

• нических почв (торф) и субстратов на их основе (смесь). При этом теплопроводность смешанного субстрата на основе песка : торфа : суглинка (5.9 : 1 : 4.4 по массе соответственно) в области низких значений влажности практически совпадает с зависимостью λ(θ) для образца торфа.

• -    при засолении теплопроводность минеральных почв снижается ввиду увеличения дисперсности. Так, с увеличением концентрации соли KBr до значений, соответствующих сильной степени засоления, теплопроводность снижается с 1.3 Вт/(м*К) до 1.1 Вт/(м*К).

• -    эти свойства влияют на разброс значений теплопроводности для зональных городских почв в диапазоне от гигроскопической влажности до полной влагоемкости: для дерново-подзолистой почвы разброс составляет 0.229–1.430 Вт/(м*К), для чернозема – 0.308–1.103 Вт/(м*К), для каштановой почвы – 0.222–1.282 Вт/(м*К).

• 3. Для задания физического обеспечения динамических моделей распределения тепла в почвах типа HYDRUS-1D была исследована прогнозная возможность двух уравнений зависимости теплопроводности от влажности λ(θ), реализованных в данной модели: Чанга–Хортона и Кэмпбелла. В демонстрационных целях, при использовании исследованной выборки образцов, ни одно из уравнений не может в полной мере описать изменение теплопроводности в зависимости от влажности в органо-минеральных субстратах на основе базовых свойств (гранулометрический состав, содержание органического вещества), что ограничивает их использование для расчета температурного режима почвенных конструкций. Но оба уравнения возможно использовать для аппроксимации экспериментальных данных по зависимости теплопроводности от влажности материалов с последующим применением в HYDRUS-1D в качестве физического обеспечения.