Тепловая динамическая модель для управления технологией электролиза алюминия

Алюминиевый электролизер для производства алюминия - это прежде всего тепловой агрегат, 50 % мощности которого теряется в окружающую среду. Поэтому для управляющих систем очень важно поддерживать на электролизере такой тепловой режим, который обеспечивал бы условия эффективной работы, постоянство оптимальной толщины застывшего электролита на стенках ванны для предохранения бортовых блоков от разрушения агрессивным расплавом, а также по возможности снижать потери энергии в окружающую среду. Поэтому в математической модели, включенной в систему управления, очень важно достоверно имитировать теплообмен электролизера с окружающей средой, изменение температур жидких и твердых слоев, плавление и образование настыли (изменение формы рабочего пространства). При этом, поскольку управляющее решение принимается в режиме реального времени, расчеты должны быть очень быстрыми, мгновенными.

Некоторые блоки тепловой модели представлены в [1; 2].

Здесь рассматривается комплекс математических моделей теплообмена всех блоков алюминиевого электролизера.

Электролизер для производства алюминия представляет собой футерованную угольными материалами ванну, содержащую два жидких высокотемпературных слоя - электролит и металл. Металл в электрохимическом процессе играет роль катода. Сверху в расплавленный электролит погружен угольный анод. В работе будем рассматривать электролизер Содерберга с самообжи-гающимся анодом (рис. 1). В каждой выделенной области тепловой режим рассчитывается по соответствующим подмоделям, с учетом теплообмена со смежными областями. Уравнения теплового баланса (нульмерные модели) составляются для глинозема, корки, электролита, металла, катода, дна и боковой стенки с настылью, имеющими средние температуры.

Анодная масса

Спеченный анод

Электролит

Настыль

Металл

Подовые блоки

Глинозем, Корка

Электролит

Рис. 1. Схема для тепловых расчетов

Погруженный

Теплоизоляция, стальной кожух

Нульмерная модель для оценки динамики температуры в заданном объеме среды. Рассмотрим вывод математической модели для исследования динамики средней температуры выделенного объема среды. Пусть П - заданный объем, Г - его граница. Температура среды определяется по уравнению теплопроводности:

ср

— + div ( T • V ) d t

= div ( XV T ) + f ,

здесь T - температура, c - удельная теплоемкость, р - плотность, X - коэффициент тепло-

проводности, V - вектор скорости движения среды, f - внутренние источники тепла.

Граничные условия на границе Г составляют

xd T = Q Г , о n

V = 0.

Проинтегрируем уравнение (1) по объему ^p :

ср [— d П + ср j div (TV ) d Q =

P ^d t ^                .        (2)

= j div (XV T) dP + j fdQ n            n

Введем средние значения температуры и источника в рассматриваемом объеме:

)

T = - Td П , — = — д—d П , f = — [ fd P . P p dt n p d t        P p

Учитывая формулу Гаусса-Остроградского:

J div ( A ) d Q = J A • nd! , n            Г

к

i — j

— 1

Az- AZ;

= 2 —i- + — j

X X_f

V 1 j 7

.

из (2) получаем

)

)

cp Q— + cp ТГ¥_пГ =J ( x ) dr + Q f . (3) dt Г "  Г    d n

Для известных средних температур в смежных слоях теплообмен между ними вычисляется по (8), (9).

d Г,

Так как V _r= 0, X—_r= Q_T , то из (3) следует n ¹ d n ¹¹

)

)

c М d- = J Q Г d r + Q f ,      (4)

dt Г где M = p Q - масса среды в объеме П .

Следовательно, средняя температура явно не зависит от скоростей течения среды, однако от характеристик течений и неравномерности распределения температуры, зависят потоки через границу Q _Г .

При использовании модели (4) эффекты конвективного переноса турбулентного обмена можно учитывать с помощью эффективного коэффициента теплопроводности. Этот коэффициент оценивается на основе использования натурных данных для исследуемого объекта.

Теплообмен в горизонтальных слоях расплавов и катода. Тепло, полученное от прохождения электрического тока, выделяется большей частью в электролите, здесь же оно и расходуется на основную реакцию. Теплообмен в областях глинозема, корки, электролита, металла, катода, дна описывается уравнениями относительно средних температур: _ˆ

c эМэ • dT ^ = Q 1 + Q ан dt

Q Э — Н

;

Q Э — M

Q _Г

Q p — Q Э — кор

ˆ dTМ c МММ     = Q Э—М dt

^Q М — Н

Q M — K ;

dTГ cГМГ •     = Qкор—Г dt

^Q Г — ат ;

Способ оценки теплообмена между смежными слоями. Рассмотрим две произвольные смежные области « i » и « j ». Оценим теплообмен между данными областями с использованием одномерных стационарных приближений:

ri= ai+ biz, rj = aj+ bjz , где z – координата, направленная поперек слоя; Ti, Tj – температуры соответствующих слоев. Отсюда для средних температур в рассматриваемых слоях получаем соотношения:

r’_i = a i + 0,5 b i A z i ; Г j = a j + 0,5 b j A z j , (5)

где A z i , A Z j - толщины соответствующих слоев.

На границе раздела слоев выполняются условия непрерывности температуры и потоков тепла:

^ai ^{+ b}i ^A z i = ^aj ; ^X i b i= ^X j b j .         ⁽⁶⁾

Теплообмен между слоями рассчитывают по формуле

Qi ; = Si Xbi ,            (7)

I — j      I — j ll'

где S i _— j - площадь границы раздела слоев.

Определим теплообмен между рассматриваемыми слоями по средним температурам

Q i - j = S i — j K i — j ( T j — T i ),         (8)

здесь K i _— j - коэффициент теплопередачи. Из соотношений (5)–(8) находим

dT кор

^C кор М кор • dt ^{— Q} Э — кор

dT cKМ к • ~77 = QМ—к dt

Q кор — Г ^;

^QK — дн ^{+ Q}q к ^;

_ˆ dT _дн c дн^1¥1дн    dt    Q K — дн

Q дн — ат ,

где T_i

слоев;

– средние температуры Q ₁ – приход тепла от

электролите; Q _ан

–

соответствующих

электроэнергии в

теплообмен с анодом;

c_i – удельные теплоемкости соответствующих материалов; М _i – массы соответствующих областей; Q _Г – потери тепла на нагрев и растворение глинозема; Q _Р – расход тепла на основную реакцию; Q_qк – тепловой поток от внутреннего источника тепла в катоде. Потоки тепла через границы соответствующих слоев рассчитывают по формулам

^Q Э — н = S Э — н •« Э — н ^(ГЭ ^{— Г} л ^Э ик ) ^- тепловой Поток Из электролита в настыль;

T _лик – температура ликвидуса электролита;

Q Э — М = S Э — М • к Э — М (Г_Э — Г м ) - тепловой поток из электролита в металл;

Q э — кор = X э b э S э — кор - тепловой поток из электролита в корку; ( λ_Э – теплопроводность электролита);

Q кор - Г = ⁵ кор - Г "  к кор - Г ^{( Т} кор ^{- Т} г ) ^- теплОвОй пОтОк от корки к глинозему;

Q М - к = 5 М - к • к М - к (Т м - Т ) — тепловой поток из металла в катод;

Q М - н = ⁵ М - н "^а М - н ^{( Т} м ^{- Т} лМк ) ^{- тепловой поток} из металла в настыль ( Т _л^М_ик – температура ликвидуса в слое металла);

Q Г - ат = ⁵ Г - ат "^а Г - ат ( ^Т г| _z = 0 ^- T ат ) ^{- тепловой поток} из глинозема в атмосферу, ( Т _Г| z - температура поверхности глинозема);

QK_дн = 5 дн • к дн(Т - Тдн) - тепловой поток из к дн к дн к дн х к дн х угольного катода в теплоизолирующее дно;

Q дн - ат = ⁵ дн - ат ^^а дн - ат ^{( Т} дн|д ^{- Т} ат )    ^{- тепловой}

“дн поток с наружной поверхности дна в атмосферу. Здесь 5 э-н ,5 э-м ,5 Э-кор,5м-н,5 М-к,5 кор-Г,5 Г-ат, 5к-дн, 5дн-ат - площади соответствующих границ. Коэффициенты теплоотдачи аГ-ат, адн-ат, аЭ-н, аМ-н считаются заданными.

Для оценки коэффициентов теплопередачи к_ij между горизонтальными слоями и нахождения профиля температур (в вертикальном направлении) используется стационарное приближение:

T i = d i + b i z ,                 (11)

отношениям (11), (12)

T дн Δдн

.

По уравнению (10) в рассчитываем выражения

определяются

стационарном для начальных

T rl z = 0 .

случае значе-

ний средних температур в горизонтальных слоях:

т дн

Т Г = Т ат

b 1 -Р 2 b 2 +^p 2 ^a 2 ^b a 31

a 13    ^р 2 a 23

a ₁₁ b ₃

a 31

,

т = к

ˆ b 2  a 23 Тдн

a 21 b 3

a 31

а 22

а 21 а 32

а 31

,

ˆ

ТМ =

а 32 ˆ

Т к а ₃₁

+ - b ^, a ₃₁

^{+ а} Э - кор

т кор

= ТГ +

где р 1 =

Тк дн

-L-+^Аг.

(« Г-ат 2Хг J

⁵ Э - кор ^а Э - кор

S гК г кор - Г кор - Г

^А дн

А

( Т ^ˆ Э

- Т л ^Э ик ), (13)

( Т э - Т л ^Э ик ),

ам . Ак + Ада +1

;

_v 2Х М ^X к х дн    ^а дн - ат _у

где 0 <  z <А z i , i = 1,2,3,4,5,6; A z i - высота соответствующих областей; i = 1 (Г) - слой глинозема; i = 2 (кор) - слой корки; i = 3 (Э) - слой электролита; i = 4 (М) - слой металла; i = 5 ( к ) - слой катода; i = 6 (дн) - дно.

Произвольные постоянные b_i , d_i определяют-

кк-дн an = р 1; a12 =-------; а13 =- дн-ат

1 + ^ ^{к -д}^ 1 ;

ОС

V   ^а дн - ат у

^b1 = ^{( р} 1   ^{1) Т} ад ^; а 21 = ⁵ М - К^к М - к ^;

ся по условиям равенства температур и потоков на границе раздела слоев:

а 22 = ^{- ( 5} М - К^к М - к ^{+ 5}К - дн ^кК - дн ) ^;

а 23 = ⁵К - дн ^кК - дн ^;

b2 = - QqK ;

d Г = Тат +      bЭ , bкор = Z'1 bЭ , bГ = у2- bЭ , аг-ат              Хкор             Хг

а 31 = ⁵ Э - М ^а Э - М ^{+ 5} М - н ^а М - н ^{+ 5} М - К^к М - К ^;

а 32 = ⁵ М - К^к М - К ^;

λ bМ = . b Э , Ьк λМ

X Ьэ, X к

b дн = ■   ^X Э b Э ,

^X дн

^b 3 = ⁵ Э - М ^а Э - М ^Т Э ^{+ 5} М - н ^а М - н ^Т лик

-

⁵ Э - м Р 1 q хим .

d кор = d Г ⁺ b Г ^А Г , d Э = ^Т лик , d М = d Э ⁺ b Э ^А Э , ⁽¹²⁾

d к = d м + b М ^А М ,      d дн = d к ^{+ Ь}к ^А к ,

а 12

Р 2 =---- а22

а ₁₁ а ₃₂ а ₃₁ а 21 а 32

.

bэ =

дн T ат

Э T лик

а 31

X э

+ ^А М + ^А к + ^А к + —¹— V ^Х Э ^Х М ^х к ^Х дк ^а дн - ат

Коэффициенты теплопередачи к _{кор - Г}, к _{Э - М}, к _{М - к} , к_{к - дн} вычисляются по формуле (9). По со-

Средняя температура электролита Т ^ˆ _Э считается заданной.

Для оценки а _Э - _Н получаем соотношение

^а э - н

Q 1 ^- Q a 3 - Э ^- Q 2 - M ^- Q T ^- б рг ^- 6 Э - кор ^-Р q хим ^ а 3 - Э 5 Э - н ( Т э - Т ^: . >

Теплообмен через бортовую футеровку с учетом настыли. Настыль контактирует непосредственно с электролитом или металлом, стальной кожух с окружающей средой (рис. 2).

Решение этой системы с учетом формул (15)

имеет вид

= т ат

+ а Э - н ( Т э - Т л ^Э ик ) ^а 1 - ат

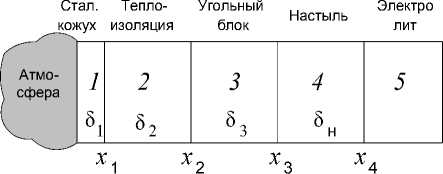
Рис. 2. Схема бортовой стенки

, а Э - н ( Т э - Т ЛИк )

к 2 - 1

' 0 _^0   ^а Э - н ^(ТЭ ^{- Т} ЛИк )

3 = т2 + к 3-2

ˆ0

T ₄

' 0 , а э - н ( Т э - Т ЛИк )

к 4 - 3

δВ области 1 используется только стационарное приближение в силу малой толщины стального кожуха и большого значения коэффициента теплопроводности стали. Для слоев теплоизоляции, угольного блока и настыли решается неста- ционарная задача:

c2М2 • -T7 = Q3-2 - Q2-1; dt c3М3 • T = Q4-3 - Q3-2; dt

ˆ c 4 М 4 • —4 = Q5-4 - Q4-3 + Q фТ; dt

Q 2 - 1 = Q 1 - ат .

Тепловые потоки определяются по следующим формулам:

ˆ

^Q 1 - ат ^а 1 - ат ( ^Т 1 Т ат ) S 1 - ат ,

Q 2 - 1 = к 2 - 1 ( Т 2 - Т 1 ) • S 2 - 1 ,

ˆˆ

^Q 3 - 2 = к 3 - 2 ^{( Т} 3 ^{- Т} 2 ) • ^S 3 - 2 ,

ˆˆ

^Q 4 - 3 = к 4 - 3 ^{( Т} 4 ^{- Т} 3 ) • ^S 4 - 3 ,

Q 5 - 4 = а э - н ( Т э - Т ЛИк ) • S 5 - 4 ,      (15)

_онаст_=п . 5 4 ^{+ 1} -5 4             f^ 5 ^ Y

^{Q фаз    Р н} L ^н     A t     S ^{5 - 4}, к ^{- j} 2 _Х ⁺ _Х ,

V i ^j 7

где T ^ˆ _i – среднее значение температуры в i -м слое; S i - j - площади соответствующих границ слоев; Q фИГ — тепло фазового перехода; р _н - плотность настыли; L _н – скрытая теплота плавления настыли; М _i – массы соответствующих областей.

Начальное приближение находят, решив стационарную задачу:

Q 3 - 2 - Q 2 - 1 = 0,

Q 4 - 3 - Q 3 - 2 = 0,

Q 5 - 4 - Q 4 - 3 = 0,

Q 2 - 1 = Q 1 - ат .

Для оценки динамики толщины настыли используем стационарные приближения в горизонтальном направлении:

T = - i + bx , 0 <  x <5 i , i = 1, 2,3, 4 .

Для средних температур в слоях имеем

T = - i + 0,5 b i 5 i .               (17)

Считаем, что средние значения температур известны. По условиям непрерывности температур на границах между слоями и на границе фазового перехода получаем уравнения для определения - i , b , 5 4 :

- 1 + b 1 5 1 = - ₂, - ₂ + b 2 5 ₂ = - ₃ ,

-3 + b35 3 = -4, -4 + b45 4= TЛик , р нLн -5^ = X 4b4 - а Э-н (^Гэ - ТлИк).     (18)

dt

По (17), (18) при = 0 находим начальное dt значение 5 04 :

5 4 = 2 Х ^{4( т} л ^{ик -} T 4 ) .        (19)

^а Э - н ^{( Т} Э ^{- Т} лик )

В нестационарной задаче для определения толщины настыли получаем уравнение

• - 5₄      Г^Э -Т

• р н L н    ⁴ = 2 Х 4 т л^к—^ - а Э - н ( 7 ; - Т лИк ).

• -t          5 4

Численное решение этого уравнения имеет вид

• 5 4 ^{+ 1} = 0,5 f5 4 - ^A t •а    (^ 7 э - T ЛИк ) ) +

V       р н L н              7

Стационарная модель анода. Оценка положения границы спекания. Для построения упрощенной тепловой модели необожженного анода Содерберга выделим три характерные области: сверху жидкая анодная масса, далее спеченный анод, разделенный, в свою очередь, на погруженную и непогруженную в электролит части (рис. 3). Непогруженные в электролит зоны имеют сбоку стальной кожух.

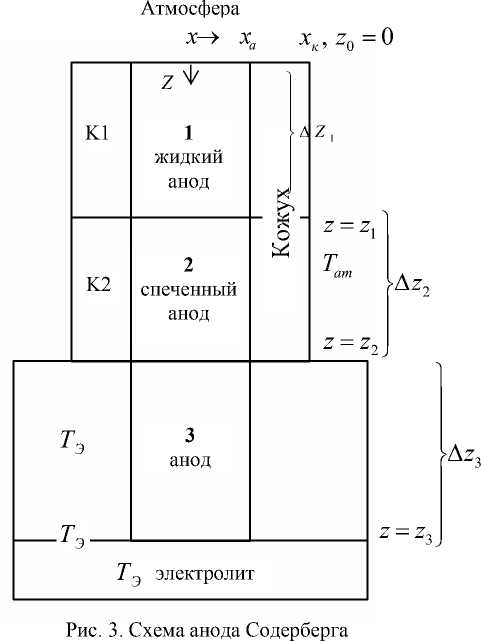
ния a _{a 1 - ат}, a _{a 3 - Э} , а _{кож - ат} считаются заданными, ^Ka 1 - а 2 , ка 2 - а 3 ^нахо д ^{ят по} формулам ⁽⁹⁾ . Формулы для потоков Q j _{кож - ат} получены с использованием одномерных стационарных приближений в горизонтальном направлении. T_a 1| z = 0 - температура жидкого анода на границе с атмосферой. Для нахождения этого значения температуры анода и оценки положения границы спекания используем стационарные приближения в вертикальном направлении:

T ai = d i + bz , 0 <  z Z i , i = 1,2,3,

где A z i - высота соответствующих областей. От-

сюда для средних температур получаем соотношения

T ai = d i + 0,5 b i A Z i .

Считаем, что средние значения температур в областях анода известны. По условию непрерывности температур на горизонтальных границах получаем d 1 + b1A z 1 = d2, d2 = Тсп, d2 + b2 A z2 = d3, (22)

здесь T _сп – температура спекания жидкого анода. В стационарном случае на границе раздела жид-

кого и спеченного анода выполняется равенства потоков тепла:

X 1 b 1 = X 2 b 2 .

По соотношению (22), (23) находим

условие

T a 1

I _z = 0 = d 1 = 2 T a 1 - Т сп ,

Потоки тепла через границы выделенных областей определяют по формулам

A z =-----

X 1 ( T сп

X 1 z 2 ( Т сп -

ˆ

T a 1 ) _ˆ

- T a 1 ) + X 2 ( T a 2 - Т сп )

.

Q a 1 - ат    S a 1 - ат *^а а 1 - ат ( T ai 1|

I z = 0

^^^^^^е

т )

ат ,

Для стационарного состояния имеют уравнения:

место

ˆˆ

Q a 1 - а 2    S a 1 - а 2 к a 1 - а 2 ⁽ T a 2 Ta 1 ),

Оз i=S з i ^- к э -> (Т 1 — Тз)        (21)

V- a 2 - а 3      a 2 - а 3     a 2 - а 3 a 3      а 2 ,

Q a 1 - а 2 - Q a 1 - ат

^^^^^^^^.

^Q 1кож - ат    ⁰ ,

Q a 2 - а 3 ^- Q a 1 - а 2 ^{- Q} 2кож - ат ^{+ Q} 2 q = ⁰ ,

ˆˆ

Q a 3 - Э    S a 3 - Э ^а a 3 - Э ^{( Т} Э   ^Та 3 ) S a 3 - э З q хим ,

Q a 3 - Э - Q a 2 - а 3 + Q 3 q = 0,

Q j кож - ат

S „ .

j кож - ат

здесь Q _{2 q} , Q _{3 q} – внутренние источники тепла от

Н а

( T aj

^^^^^^в

Т )

ат ,

j = 1, 2.

x

Здесь н = -a - + aj

а кож -ат

, S i _- j- - площади со-

ответствующих границ, T_аj – средняя температу-

ра в j -й области, T _ат – температура воздуха, Р q _хим - теплота Пельтье на границе анод-электролит, X j- - эффективные коэффициенты

прохождения электрического тока в соответствующих областях. Подставляя в эти соотношения формулы (21) для потоков тепла, получим систему линейных уравнений для определения T ^ˆ _{а 1}, T ^ˆ _{а 2} , T ^ˆ _{а 3} . Решение этой системы имеет вид

ˆ   ˆˆ

Та 1 = A1IA 2 , Т а 2 = A 12 T a 1 ⁺ A 42 ,

ˆˆ

Т а 3 = A 13Ta 2 ⁺ A 23 ,              ⁽²⁵⁾

где А 33 = ^Sa 3 - Э ^а а 3 - Э + S a 2 - а 3 ^ка 2 - а 3 ;

теплопроводности, учитывающие стальные токоподводящие стержни ( j = 1, 2). Кроме того, значе-

S a 2 - а 3 к а 2 - а 3

А 13=      .        ; А 23"

13                       23

А

ˆ

^Q 3 q ^{+ S}a 3 - Э ^а а 3 - Э Т Э S a 3 - э Р q хим .

;

2кож - ат

А 22 ⁼ S a 2 - a 3 к а 2 - а 3 (1 ^- А 13 ) ⁺ S a 1 - а 2 к а 1 - а 2 ⁺           ;

^µ а 2

А12=

S a 1 - а 2 к а 1 - а 2

А 22

;

A42=

2кож - ат

Q 2 q ⁺ S a 2 - a 3 к a 2 - a 3 A 23 ⁺           T ат

µ _{а 2}

A ₂₂

;

A 1 = S a 1 _{- a 2} Ka 1 - a 2 A 42 + S_{a 1 - am} α a 1 - am ( T am + T cn ) +

1кож -am

+          T _am ;

^µ a1

A ₌ 2 S          ₊ 1кож-am

2        a 1 _- am ^α a 1 - am

^µ a1

-

S a 1 - a 2 ^K a 1 - a 2 A ¹² .

Рассмотрим алгоритм определения стационарного приближения для анода:

– этап 1. Из соотношений (25), (26) по заданной температуре электролита Т ^ˆ _Э находим средние значения температур в слоях анода 1, 2, 3;

– этап 2. По формуле (24) уточняем высоту слоя жидкого анода – Δ z ₁ ^m .

Далее переходим на этап 1. Итерации повто-

ряются до выполнения условия m + 1        m

Δ z1m+ - Δ z1m ≤ε.

Порядок выполнения численных расчетов. Перед началом каждого динамического расчета вычисляется стационарное распределение температур, тепловых потоков, толщин настыли в металле и электролите, высоты спекания анода. Задаются начальные значения средней температуры электролита, температура воздуха, приходы тепла от электроэнергии в электролите, катоде и в аноде. По соотношениям (13), (16), (19), (24), (25) определяются начальные значения температур в рассматриваемых областях, толщины настыли и положение границы спеченного анода. Найденное стационарное состояние соответствует введенным начальным технологическим условиям и заданным параметрам.

Далее на каждом временном шаге последовательно решаются системы уравнений (10), (14), по формулам (20), (24) уточняются толщины настыли и положение границы спеченного анода. Система (14) решается так же, как для слоя металла.

Динамика теплообмена электролизера определяется по изменениям прихода тепла от электроэнергии, которые выводят систему из равновесия: изменяются температуры выделенных областей, толщины настыли. Вследствие этого увеличиваются или уменьшаются теплопотери в атмосферу через днище, борта электролизера, анодную массу и кожух анода. Плавление настыли или затвердевание электролита приводит к изменению массы электролита. В результате электролизер приходит в новое стационарное состояние с повышенными (пониженными) температурами расплавов, повышенными (пониженными) температурами наружных поверхностей, уменьшенными (увеличенными) толщинами настыли.

На основе схематизации электролизера в виде характерных областей и использования нульмерных моделей разработана тепловая динамическая модель, предназначенная для эффективного решения задач управления технологией электролиза алюминия.