Тепловое состояние наноспутника при нестационарном тепловыделении на радиоэлектронных элементах полезной нагрузки

Наноспутники являются быстро развивающимся классом космических аппаратов (КА), возможности которых позволяют использовать их для научных, мониторинговых, образовательных целей. По современной классификации [1] (таблица 1) к наноспутникам относятся КА с массой от 1 до 10 кг.

В настоящее время разработка наноспутников основывается на наиболее распространенном стандарте CubeSat [2]. Данный стандарт предлагает блочную концепцию КА с базовым типоразмером 100×100×100 мм и массой до 2 кг (форм-

Таблица 1

Классификация спутников по массе, кг

Большие Средние Мини Микро Нано Пико 1000< 500- 100- 10- 1- <1 фактор 1U). В соответствии со стандартом CubeSat на основе типоразмера 1U могут формироваться КА до 12U и массой до 24 кг (таблица 2). Как видно из таблицы 2, к наноспутникам относятся КА с форм-факторами от 1 до 3U.

Особенностями наноспутников являются относительно небольшие затраты на проектирование, производство и выведение на орбиту. Корпуса таких КА негерметичны, а в полезной нагрузке используются самые доступные радиоэлектронные

Таблица 2

Форм-факторы и массы КА по стандарту CubeSat

Форм-фактор	1U	1.5U	2U	3U	6U	12U
Масса, кг	2,0	3,0	4,0	6,0	12,0	24,0

I/        I —

ОСМИНЕСКИЕ

АППАРАТЫ VI

ТЕХНОЛОГИИ нш

комплектующие, не сертифицированные для условий космического полета [3]. Работоспособность таких комплектующих сохраняется в температурном диапазоне от –40 до 85 °C, аккумуляторной батареи от –20 до 60 °C [4]–[7].

Одной из основных задач, возникающих при разработке наноспутника, является обеспечение температурного режима полезной нагрузки [7–12]. Если для КА с форм-фактором 1U доступны пассивные методы терморегулирования [6], то для КА с форм-фактором > 2U допустимы более эффек- тивные методы, например использование тепловых труб [12].

В условиях орбитального полета КА подвергается тепловому нагреву со стороны внешних источников излучения, а на радиоэлектронных элементах полезной нагрузки происходит выделение тепловой энергии при значительном уровне мощности. Под воздействием этих факторов в элементах конструкции КА формируется нестационарное, неоднородное поле температуры.

Цель настоящей работы - оценка теплового ре- жима радиоэлектронных компонент наноспутника с форм-фактором 1U при его движении по заданной орбите и при известных режимах работы полезной нагрузки. Следует отметить, что данная работа является развитием [13] в направлении более точного описания внутренних тепловых источников. В [13] радиоэлектронные компоненты явно не рассматривались, тепловыделение на электронных платах полагалось одинаковым, постоянным, равным усредненной величине, и распределялось равномерно по объему плат. В настоящей работе тепловыделение сосредоточено в объемах радио-

Том 8

электронных компонент, которые размещены на платах и имеют с ними тепловой контакт.

1.    Постановка задачи

Рассматривается наноспутник CubeSat с формфактором 1U (рисунок 1). Конструкция КА включает: рельсы 1, которые вместе с соединительными элементами 2 образуют силовой каркас; платы 4–8, связанные с корпусом элементами крепления 3; стенки корпуса 9, закрепленные на силовом каркасе. На стенках 9 располагаются панели солнечных батарей. Начало системы координат, связанной с КА, находится в геометрическом центре корпуса.

Функционально платы 4–8 включают: приемник-передатчик, бортовой компьютер, систему навигации; аккумуляторную батарею и систему управления электропитанием (СУЭ); систему управления движением (СУД). Расстояние между платами составляет около 15 мм.

Электронные компоненты полезной нагрузки представляются параллелепипедами, которые контактируют своими гранями с платами (рисунок 1), тепловое сопротивление между компонентами и платами считается пренебрежимо малым. При этом другие связи, например паяные соединения, не рассматриваются. Тепловая мощность, выделяющаяся на радиоэлектронной плате, равномерно распределяется по объему соответствующих параллелепипедов. Платы 4-8 и стенки корпуса 9 не имеют теплового контакта с рельсами 1. Остальные элементы конструкции КА соединены между собой плотно, так что в местах соединения не вносится дополнительного теплового сопротивления.

КА движется вокруг Земли по круговой орбите, имеющей высоту 300 км. Орбита КА лежит в плоскости орбиты Земли. Ось Y системы координат, связанной с КА, направлена к центру Земли, ось X совпадает с направлением движения

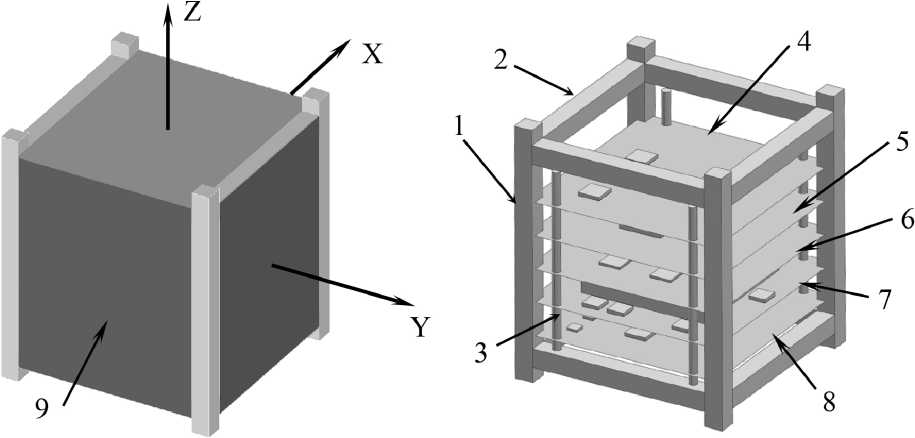
Рисунок 1. Схема КА CubeSat (форм-фактор 1U): 1 – рельс; 2 – соединительный элемент каркаса;

3 – элемент крепления плат; 4 – приемник-передатчик; 5 – бортовой компьютер;

6 – система навигации; 7 – аккумуляторная батарея и СУЭ; 8 – СУД; 9 – стенка корпуса

КА. Рассматриваются дни осеннего равноденствия и зимнего солнцестояния, которые различаются величиной солнечной постоянной.

Тепловое состояние КА определяется поглощенным излучением от внешних источников и тепловыделением от внутренних источников. Полагается, что КА в момент времени t =0 оказывается на орбите с однородным распределением температуры T 0 , т.е. влияние на тепловое состояние КА процесса его выведения на орбиту не рассматривается.

Обозначим через r радиус-вектор точки с координатами (x, y, z), а также x=x 1, y=x 2, z=x 3. Тогда температурное поле в КА в момент времени t описывается уравнением cpTt = k • T + qv (1) с начальными условиями

T(t = 0,r) = To, (r), r g V (2) и граничными условиями k ' T,n = qrad(out), r G Sout, (3)

k • T ,n = q rad(in ) , r G S n ,                  (4)

где V - объем, занимаемый КА; T = T ( t , r ) - температура материала КА; S_out , S_in – внешние и внутренние поверхности, ограничивающие V ; n - вектор нормали к поверхности; c = c ( r ), р = р ( r ) и k = к ( r ) - удельная теплоемкость, плотность и теплопроводность сплошной среды; q V = q V ( r ) - плотность внутренних тепловых источников; q rad ( out ) и q rad ( i _n ) - результирующие плотности потоков излучения на поверхности S_out и S_in , которые представляют собой разности между поглощенными и излученными ими потоками энергии; i – индекс компоненты x_i , i =1,2,3.

Величина qrad(out) из (3) равна qrad(out)  qsun + qalb + qearth + qaer  qsat.

q_sun – падающий на КА поток излучения от Солнца, q sun =^a out Q sun ^{( n} • n sun ) Ф , где ^Q sun ^{- солнечная по} стоянная, 1357 Вт/м² (осеннее равноденствие) и 1411 Вт/м² (зимнее солнцестояние); n - вектор нормали к внешней поверхности ко р пуса КА; a _out - коэффициент поглощения внешней поверхности корпуса КА; n_sun – вектор, направленный на Солнце; φ – параметр затенения (затенение φ=0, нет затенения φ=1).

q_alb – излучение, отраженное от Земли, q_alb =α _out Q sun Ф sat- earth b , где Ф sat- earth – фактор видимости [14]; b – коэффициент альбедо, b = 0.3.

q_earth – по т ок теплового излучения от Земли, q earth =a out Q earth Ф sat-earth , где Q earth - плотность инфракрасного излучения Земли, 237 Вт/м².

q_aer - поток, обусловленный аэродинамиче с ким нагревом. На орбитах с высотами ≥ 300 км величиной q_aer можно пренебречь [7].

qsat – собственное излучение КА, qsat =MsoutT4 -aoX), где T» - температура от- крытого космоса, 2.7°К, еout - коэффициент излучения внешней поверхности корпуса КА.

Полный расчет величины q_{rad ( in} ) из (4) с учетом многократных отражений и поглощений излучения на внутренней поверхности S_in является сложной задачей. Поэтому используется упрощенный подход, приведенный в [14], в котором реальные поверхности условно считаются диффузносерыми. В этом случае коэффициенты излучения ε и поглощения α полагаются равными.

• 2.    Геометрические, теплофизические и конечно-элементные параметры

Конечно-элементная модель имеет следующие геометрические параметры: рельсы 1 (рисунок 1) и соединительные элементы 2 имеют сечение 8,5^8,5 мм, рельсы имеют длину 113,5 мм; толщина стенок корпуса 9 составляет 1,27 мм, на их внешних поверхностях находится фотоэлектрический слой толщиной 80 мкм; толщина плат равна 1,6 мм.

На рисунке 2 показано расположение радиоэлектронных компонент на платах.

Размеры радиоэлектронных компонент: 5×5×1 мм, 8×8×1,5 мм, 10×7×1,5 мм, 10×10×1 мм, 10×10×1,5 мм, 15×15×2 мм, 20×20×2 мм. Размеры аккумуляторной батареи 60×60×9 мм.

Физические, термические и оптические свойства материалов, необходимые для решения задачи (1)-(4), приведены в таблице 3. Все характеристики (кроме корпусов электронных компонент) взяты из [13]. В качестве свойства корпусов электронных компонент использовались свойства полимерного компаунда для производства корпусов транзисторов [15], а оптические свойства поверхностей соответствуют свойствам черной эпоксидной краски [16].

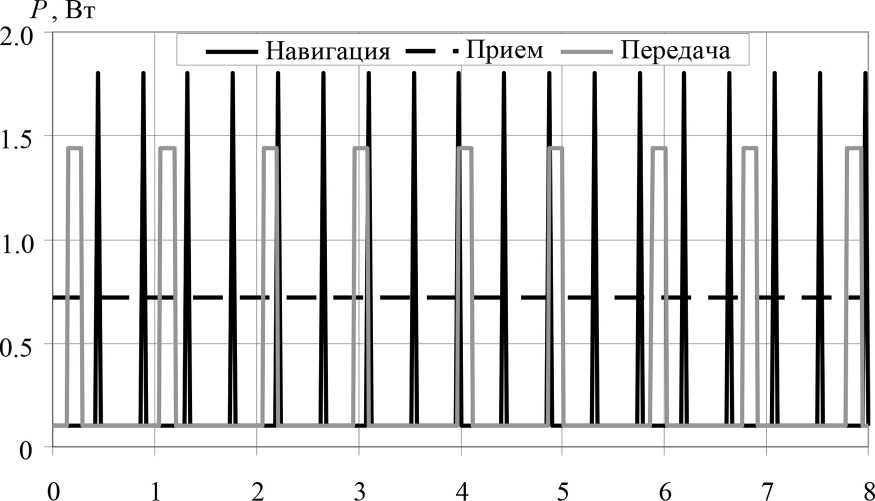
Плотность внутренних тепловых источников q_V из (1) определялась по зависимостям мощности нестационарного тепловыделения на платах радиоэлектронных систем КА из [17], графики которых показаны на рисунке 3. На этих графиках единица времени равна времени одного оборота КА вокруг Земли. Для круговой орбиты с высотой 300 км время одного оборота вокруг Земли составляет 5.422 4 0 3 с. Ввиду того, что в [17] были представлены зависимости, ограниченные временным интервалом 0 об. <  t < 3 об., они были экстраполированы на 3 об. <  t < 8 об. Данный интервал времени, как показали расчёты, достаточен для получения температурного поля конструкции, которое не зависит от числа оборотов, совершенных КА.

Задача (1)-(4) решается численно, методом конечных элементов. Для этого использовался конечно-элементный программный пакет

Том 8

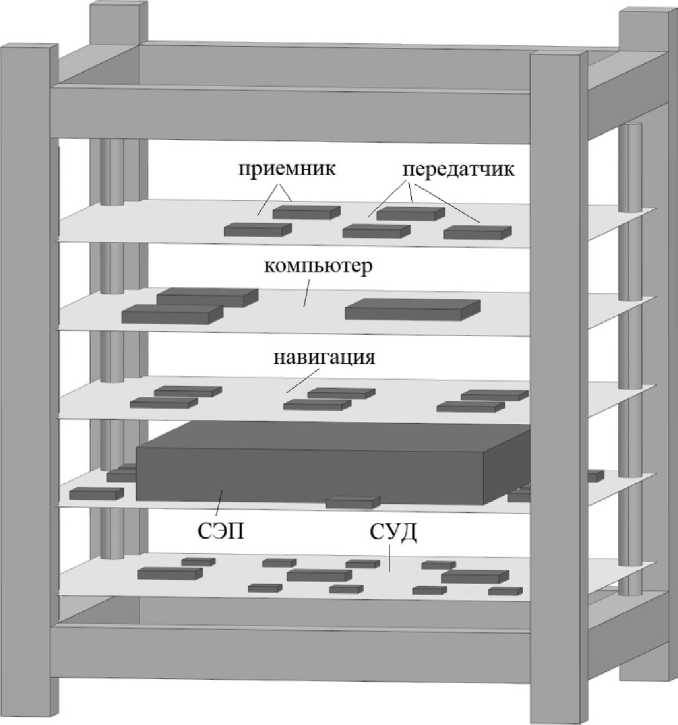
Рисунок 2. Расположение радиоэлектронных компонент на платах

Таблица 3

Элемент конструкции	k , Вт/(м·К)	с , Дж/(кг·К)	r	ε	α
Силовой каркас	140,0	948	2810	0,4	0,4
Солнечная батарея	45,5	327	6250	0,85	0,91
Электронная плата	0,64	975	2120	0,22	0,85
Батарея	23,0	1110	2247	0,7	0,85
Электронные компоненты	0,8	2000	1500	0,9	0,85

Теплофизические свойства материалов и поверхностей

SIEMENS-NX, в котором реализованы процедура решения уравнения теплопроводности и метод вычисления q_{rad ( out )} и q_{rad ( in )}. Конечно-элементная модель содержала 20000 элементов.

3.    Результаты

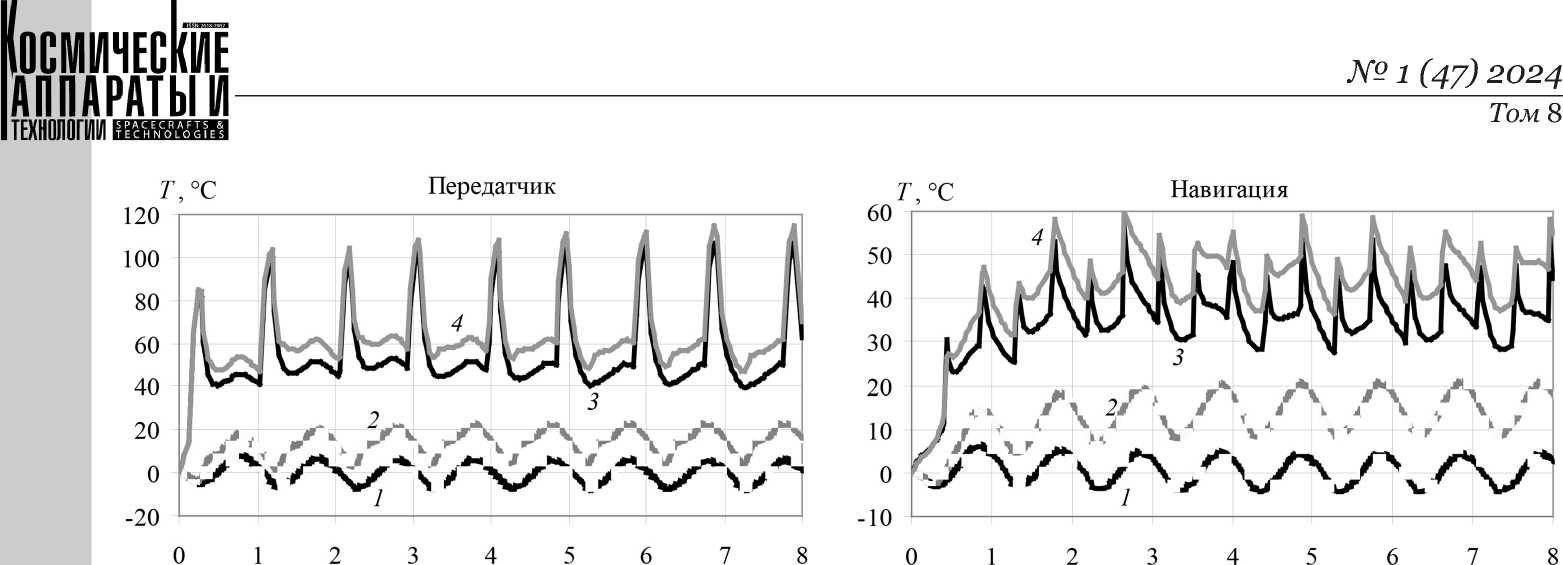
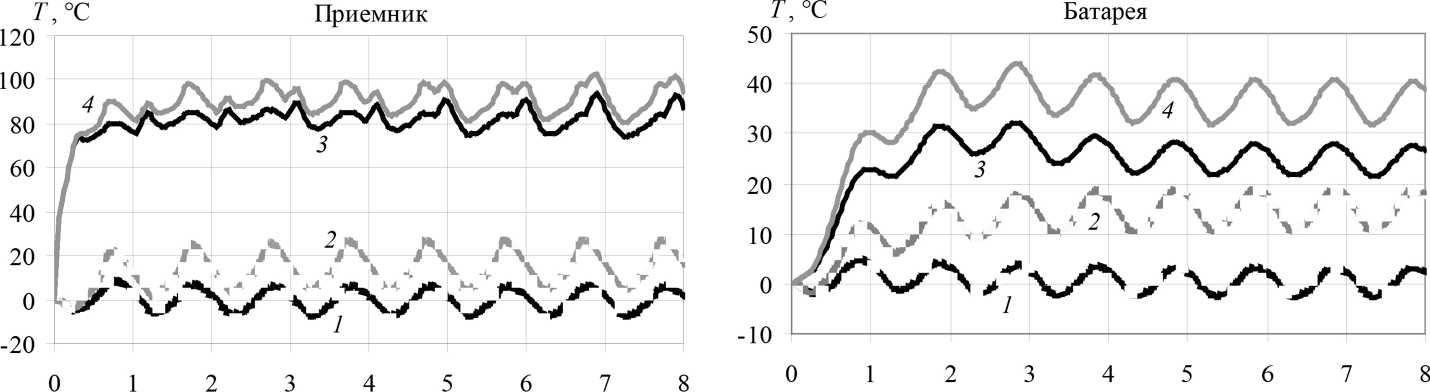
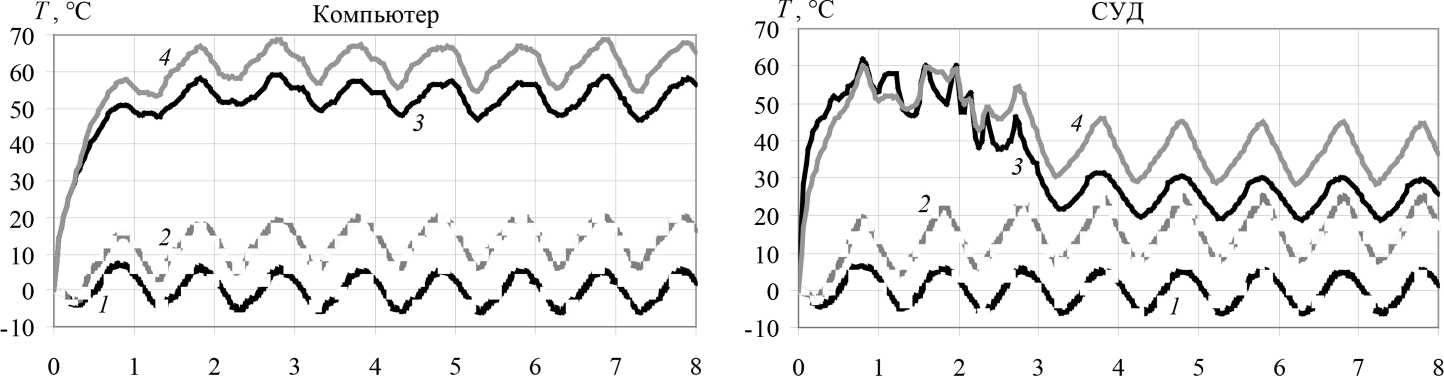
На рисунке 4 представлены результаты численного моделирования динамики температуры электронных компонент полезной нагрузки наноспутника: передатчика, приемника, аккумуляторной батареи, компьютера, навигационной системы, СУД. Рассматривались случаи без тепловыделения и с тепловыделением на полезной нагрузке для осеннего равноденствия и для зимнего солнцестояния.

Результаты показывают, что увеличение солнечной постоянной при переходе от осеннего равноденствия к зимнему солнцестоянию увеличивает температуру радиоэлектронных компонент в пределах 12,5–13,5 °C. Орбитальное движение приводит к осцилляциям температуры с перио- дом, равным одному орбитальному обороту. Это особенно заметно в случае отсутствия тепловыделения. При этом величина осцилляций зависит от положения платы в общем пакете плат. Так, для осеннего равноденствия величина осцилляций составила: передатчик и приемник - 13,7 °C, компьютер – 10,8 °C, навигационная система – 8,5 °C, аккумуляторная батарея – 5,8 °C, СУД – 11,2 °C. Наибольшие осцилляции наблюдаются на крайних платах, на внутренних платах осцилляции меньше, что объясняется их экранировкой от стенок корпуса.

При внутреннем тепловыделении температуры радиоэлектронных компонент значительно увеличиваются. Величина температурного прироста определяется средней мощностью тепловыделения. Наиболее интенсивно температура увеличивается на первом обороте вокруг Земли. Последующая температурная динамика определяется режимом работы платы, влиянием соседних плат, орбитальным движением КА. Почти во всех случаях, кроме платы с навигационной системой

t, об

а

t, об

б

Рисунок 3. Тепловые мощности радиоэлектронных систем КА

(рисунок 4), изменение температуры во времени приобретает периодический характер. Наиболее сложная картина наблюдается для платы с навигационной системой. Такая температурная динамика объясняется действием на плату мощных импульсов тепловыделения (рисунок 3), а также тепловым влиянием соседних плат.

Результаты расчетов показывают, что при внутреннем тепловыделении температура аккумуляторной батареи лежит в пределах от 0 до 44 °C. Температуры электронных компонент плат бортового компьютера, навигационной системы, СУД находятся в пределах 0 до 69 °C. Эти значения температур не выходят за температурные пределы, которые приведены в разделе «Введение». В то же время передатчик и приемник работают с перегревом. Температурные пики приемника при осеннем равноденствии превышают 90 °C, а температурный минимум составляет 75 °C. При зимнем солнцестоянии максимальная температура достигает 102,6 °C, а минимальная 81 °C. Для передатчика при зимнем солнцестоянии пиковые значения температуры превышают 114 °C, а температура в минимуме 48 °C. Такие температурные скачки связаны с импульсным характером тепловыделения на передатчике, причем расположение температурных пиков во времени (рисунок 3, передатчик) совпадает с расположением пиков тепловыделения (рисунок 2). Кроме того, приемник и передатчик располагаются вблизи, на одной плате и влияют друг на друга.

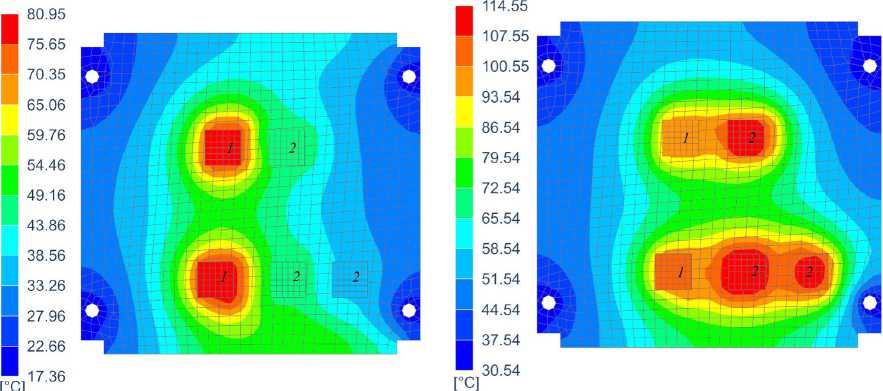
Распределения температур на плате 4 (рисунок 1) с приемником-передатчиком и на плате 7 (рисунок 1) с аккумуляторной батареей и СУЭ в моменты температурного максимума и минимума показаны на рисунках 5 и 6. Рисунок 5а соответствует состоянию КА, когда последний выходит из тени. Компоненты приемника горячие, так как он постоянно работает (рисунок 3). Через пол-оборота включается передатчик и его компоненты нагреваются (рисунок 5б), при этом частично подогреваются и компоненты приемника.

/, об                                                                             /,об

/, об                                                                            /, об

/, об                                                                       об

Рисунок 4. Температуры радиоэлектронных компонент полезной нагрузки КА:

1 – осеннее равноденствие, без тепловыделения; 2 – зимнее солнцестояние, без тепловыделения;

3 – осеннее равноденствие, с тепловыделением; 4 – зимнее солнцестояние, с тепловыделением

Температурное пятно на рисунке 6а обусловлено тем, что КА вышел из тени (батарея еще холодная) и направлен своим ребром (нижнее правое на рисунке 6а) в сторону Солнца. Через полоборота освещается грань корпуса КА, которая на рисунке 5б расположена вверху, батарея разогрета, так как в течение этого времени КА освещался Солнцем.

Заключение

Проведенное исследование показало, что температура радиоэлектронных компонент полезной нагрузки наноспутника CubeSat с форм-фактором 1U определяется следующими факторами: мощ- ностью собственного тепловыделения; тепловым влиянием соседних плат; собственным движением по околоземной орбите, положением на земной орбите. В основном температурная динамика радиоэлектронных компонент зависит от действующего режима тепловыделения. Во всех расчетных случаях температуры радиоэлектронных компонент бортового компьютера, системы навигации, аккумуляторной батареи и СУЭ и СУД находятся в допустимых эксплуатационных пределах. Под действием импульсных тепловых нагрузок большой мощности компоненты системы приемник-передатчик испытывают кратковременный перегрев.

По сравнению с работой [13] получено существенно более детальное описание теплового со-

а

б

Рисунок 5. Распределение температур на плате 4, день зимнего солнцестояния, элементы: 1 – приемник, 2 – передатчик; а – t =7,25 об., б – t =7,91 об.

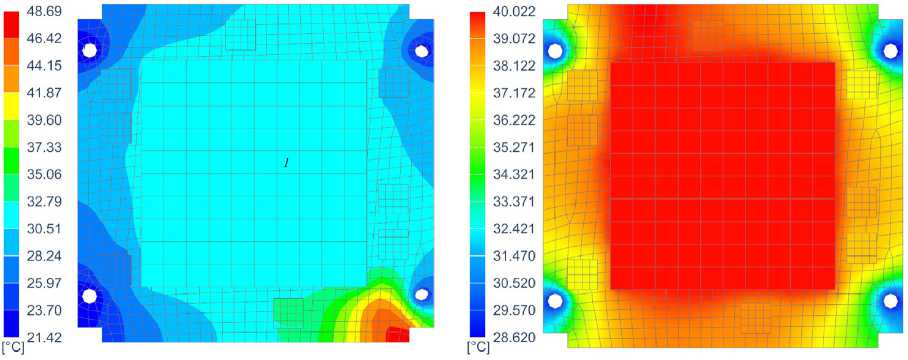
а

б

Рисунок 6. Распределение температур на плате 7, день зимнего солнцестояния: 1 – батарея; а – t =7,31 об., б – t =7,91 об.

стояния наноспутника CubeSat с форм-фактором 1U. Решение подобных задач требует точного знания: конструкции корпуса КА; теплофизических свойств материалов и поверхностей; внутренней материальной структуры радиоэлектронных компонент и способа их крепления к платам.

Работа выполнена в рамках государственного задания Министерства науки и высшего образования Российской Федерации (тема № FSWM-2020– 0036).